Application of phase diagram calculations to development of
new ultra-high temperature structural materials
YANG Ying(杨 莹)1, B.P. Bewlay2, CHEN Shuang-lin(陈双林)1, Y.A. Chang3
1. CompuTherm LLC, Madison, Wisconsin 53719, USA;
2. General Electric Global Research, Schenectady, New York 12301, USA;
3. Department of Materials Science and Engineering, University of Wisconsin-Madison, Madison,
Wisconsin 53705, USA
Received 15 July 2007; accepted 10 September 2007
Abstract: In-situ refractory metal intermetallic composites(RMICs) based either on (Nb, Si) or (Mo, Si, B) are candidate materials for ultra-high temperature applications (＞1 400 ℃). To provide a balance of mechanical and environmental properties, Nb-Si composites are typically alloyed with Ti and Cr, and Mo-Si-B composites are alloyed with Ti. Phase diagrams of Nb-Cr-Ti-Si and Mo-Si-B-Ti, as prerequisite knowledge for advanced materials design and processing development, are critically needed. The phase diagrams in the metal-rich regions of multicomponent Nb-Cr-Ti-Si and Mo-Si-B-Ti were rapidly established using the Calphad (Calculation of phase diagram) approach coupled with key experiments. The calculated isotherms, isopleths, and solidification paths were validated by experimental work. The important heterogeneous multiphase equilibria in both quaternary systems identified will offer engineers the opportunity to develop materials with a balance of properties for high-temperature applications.
Key words: intermetallics, phase diagram calculation; Mo-Si-B-Ti; Nb-Cr-Si-Ti; high temperature structural materials
1 Introduction
In searching for higher temperature materials (i.e.＞1 400 ℃) beyond the nickel-based superalloys for future propulsion systems, refractory metal-intermetallic composites(RMICs)[1] have received considerable interest[2-3]. Recent studies identified RMICs based on (Mo, Si, B) and (Nb, Si) as having great potential for turbine engine applications[2-3] because of their high melting temperatures and enhanced oxidation resistance at elevated temperatures. The RMICs based on the Nb-Si system are typically alloyed with Ti, Cr, Hf, Al[4-7] and those based on the Mo-Si-B system are alloyed with Ti and Zr[8-10] for the balance of properties such as fracture toughness, strength, oxidation resistance and creep strength.
Phase diagrams are part of the road map for materials and processing development. They have been traditionally determined exclusively by experimentation. It is meticulous, time-consuming, and difficult for obtaining multicomponent phase diagrams over wide ranges of compositions and temperatures. However, recent advances in phase diagram calculation using the phenomenological or Calphad approach[11-12] has enabled us to rapidly obtain multicomponent phase diagrams with a reduced level of experimental effort. The essence of the Calphad route is to obtain a thermodynamic description of a multicomponent system via extrapolation of the descriptions of its constituent lower order systems, normally binaries and ternaries. The term “thermodynamic description” means that a set of thermodynamic models with parameters for the phases in a system are obtained so that not only thermodynamic values of the phases but also phase diagrams of the system can be calculated.
In the present work, the application of the Calphad approach to rapidly developing thermodynamic descriptions of the quaternary Nb-Cr-Ti-Si and Mo-Si-B-Ti systems was demonstrated.
2 Quaternary Nb-Cr-Ti-Si
2.1 Thermodynamic modeling and experimental procedures
The strategy of building a thermodynamic database for the Nb-Cr-Ti-Si quaternary system starts with deriving Gibbs energy of each phase in the constituent binaries. There are six constituent binaries: Nb-Si, Nb-Cr, Nb-Ti, Cr-Si, Cr-Ti, and Ti-Si. After the thermodynamic descriptions for all the constituent binaries are established, the Gibbs energy of a phase in a ternary system can be obtained by the weighted average of those of the same phase from the three constituent binaries using geometric models, such as the MUGGIANU model[13] in the present study. This is the extrapolation method for obtaining a thermodynamic description of a ternary system. However, due to the potentially strong ternary interactions, and the possible formation of new ternary compounds, developing the thermodynamic description by extrapolation may not accurately describe the thermodynamic properties and the phase equilibria in a ternary system. In the present work, ternary interaction parameters are introduced for all constituent ternary systems. In essence, Nb-Cr-Si, Nb-Cr-Ti, Nb-Ti-Si, and Cr-Ti-Si have been subjected the similar thermodynamic modeling process to that used for the binaries. Thermodynamic descriptions are available for all the constituent subsystems: Nb-Si[14], Nb-Cr, Nb-Ti, Cr-Si, Cr-Ti, Ti-Si[15], Nb-Cr-Ti, Nb-Ti-Si, Nb-Cr-Si[16], and Cr-Si-Ti[17]. Details on thermodynamic modeling process can be referred to the original literature.
No prior phase equilibria and thermodynamic property data for the Nb-Cr-Ti-Si quaternary system were found in literature. Therefore, the new thermodynamic description for the quaternary was obtained through extrapolation. Then, alloys based on the calculated phase equilibria were selected for experimental investigation. The experimental results were used for the validation of the thermodynamic description. It was found that there was no need to introduce the quaternary interaction parameters since the extrapolated quaternary thermodynamic description satisfactorily described the available experimental data. Pandat software[18] was used to calculate the phase diagrams and solidification paths.
The alloys for this study were cast using cold crucible directional solidification[5-6] after triple melting the starting charges from high purity elements (＞99.99%). The directional solidification procedure has been described in more detail previously[5]. Samples for heat treatment were wrapped in Nb foil and heat-treated at 1 100 ℃ for 100 h in a vacuum (＜1.33×10-3 Pa) furnace, followed by furnace cooling.
All of the samples were examined using scanning electron microscopy(SEM) back-scatter electron(BSE) imaging and energy dispersive spectrometry(EDS). Phase compositions were measured by electron probe micro-analysis(EPMA), which was performed on a JEOL 733 microprobe operating at 15 kV, 20 nA, with a about 1 mm beam diameter (Japan Electron Optics Ltd., Tokyo). High purity Nb, Cr, Ti, and Si were used as standards and conventional matrix corrections (Z, A, and F) were used to calculate the mass fraction of compositions from measured X-ray intensities. The crystal structures of the phases were identified using X-ray diffraction(XRD) and electron back scattering diffraction(EBSD).
2.2 Results and discussion
With the thermodynamic description of the Nb-Cr-Ti-Si system, the phase equilibria can be calculated at any temperature and composition. In this section, only the solid-state phase equilibria at 1 350 ℃ and liquid-solid phase equilibria for selected alloys are shown, and their use in the validation of the calculated results is described.
2.2.1 Solid-state phase equilibria at 1 350 ℃ in Nb-rich region
Fig.1 shows the calculated isothermal sections of the Nb-Cr-Ti-Si system at 1 350 ℃ with the Cr content being fixed at 0, 5% and 10% (molar fraction), respectively. All of the alloy compositions are stated in molar fraction in this article. Only the Nb-rich regions are labeled since they are of the current interest. Without the addition of Cr, the phase equilibria of the Nb-rich region include two two-phase regions: (Nb)+Nb5Si3 and (Nb)+Nb3Si. With increasing Cr additions, the C14 phase becomes more stable. The stability regions of the Nb+Nb5Si3 and (Nb)+Nb3Si are reduced, and they are almost completely eliminated in the section with 10% Cr. These calculated results are well validated by the microstructural and microchemical evidence from the two annealed alloys Nb-10Cr-23Ti-15Si and Nb-11Cr-23Ti-13Si. Fig.2(a) shows the BSE image of Nb-10Cr-23Ti-15Si. Three phases can be observed in this micrograph. They are (Nb) (light gray), Nb5Si3 (medium gray), and Cr2Nb-C14 (dark gray), which is also referred to as C14. Their crystal structures were confirmed by EBSD analysis. The microstructure of Nb-11Cr-23Ti-13Si was similar to that of the Nb-10Cr-23Ti-15Si, as shown in Fig.2(b). Comparisons between the calculated phase compositions and the EPMA measurements are listed in Table 1. In view of the fact that these experimental compositions were not used in model parameter optimization, the calculated phase compositions from the initial extrapolated thermodynamic description agree well with the experimental measurements. The major composition discrepancy occurs in the composition of the C14 phase; the calculation shows a higher Cr level and lower Nb and Ti contents than the experimental values. This discrepancy mainly comes from uncertainties in the Cr-Nb-Ti system. Fine adjustment of model parameters is currently in progress to reduce the C14 phase composi-tion discrepancy.
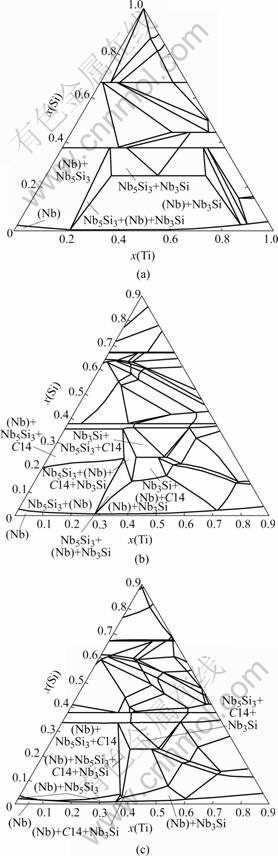
Fig.1 Isothermal sections of Nb-Cr-Ti-Si system at 1 350 ℃ with Cr being fixed at 0 (a), 5% (b) and 10% (c) (molar fraction), respectively
Fig.2 BSE images of annealed microstructures: (a) Nb-10Cr- 23Ti-15Si; (b) Nb-11Cr-23Ti-13Si
2.2.2 Liquid-solid phase equilibria in Nb-rich region
The liquid-solid phase equilibria at the Nb-rich region are described using isopleths sections and solidification path simulations. The as-cast microstructures of four alloys Nb-10Cr-23Ti-15Si, Nb-11Cr-23Ti-13Si, Nb-21Cr-23.5Ti-15.5Si, and Nb-21Cr-28Ti-13Si were used to validate the calculated results. Fig.3 shows the calculated isopleths of Nb-Si with the Si content up to 30%. The liquid phase is denoted by “L”. The Ti content in both Figs.3(a) and (b) is fixed at 23%. The Cr content in Fig.3(a) is zero while it is fixed at 10% in Fig.3(b). The calculation shows primary solidification of (Nb) and Nb5Si3 in both figures. The primary solidification of Nb3Si is only present in Fig.3(a), for which there is no Cr addition. Cr suppresses the Nb3Si primary phase region. By suppressing the Nb3Si primary solidification, the direct solidification of two-phase (Nb)+Nb5Si3 becomes possible in the Nb-Cr-Ti-Si system. This two-phase trough of (Nb)+Nb5Si3 does not exist in either the Nb-Si binary or Nb-Ti-Si ternary alloy. The calculation suggests that Cr addition helps to stabilize the Nb5Si3 and destabilize the Nb3Si. In addition, the Si content of this two-phase trough of metal (Nb) and metal silicide Nb3Si or Nb5Si3 shifts to lower Si values with the addition of Cr.
Solidification path simulations were performed on the above four alloy compositions using the SCHEIL[19] and lever-rule models. The SCHEIL model assumes no diffusion in solid and thermodynamic equilibrium is maintained at liquid/solid interface only. The lever-rule model assumes complete mixing in both liquid and solid, and the composition of solid and liquid are in thermodynamic equilibrium. The SCHEIL model predicts the fastest solidification with the local equilibrium being maintained at the liquid/solid interface. In contrast, the lever-rule model assumes that the solidification is slow enough to allow no microsegregation in solid. The solidification speed on normal as-cast or directional solidification condition usually lies between these two conditions. Both models require thermodynamic information only and are integrated into the solidification simulation module of PANDAT[18].
Table 2 Comparisons between EMPA measured and calculated phase compositions
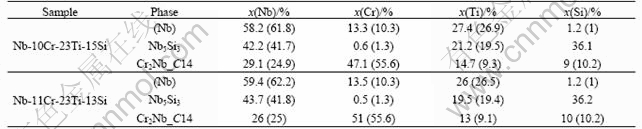
Value in parentheses are calculated phase compositions
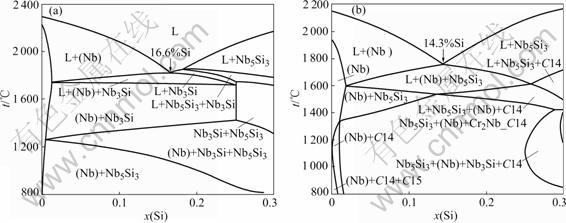
Fig.3 Isopleths of Nb-Si with Si content up to 30%: (a) x(Cr)=0, x(Ti)=23%; (b) x(Cr)=10%, x(Ti)=23%
Figs.4(a), (b), (c), and (d) show the simulated solidification paths for the Nb-10Cr-23Ti-15Si, Nb-11Cr-23Ti-13Si, Nb-21Cr-23.5Ti-15.5Si, and Nb-28Ti-21Cr-13Si alloys. The BSE images of the as-cast microstructures of these alloys are shown in Figs.4(e), (f), (g), and (h), respectively. For all four alloys, the microstructural evidence can be observed in the BSE images for the lever-rule simulation and the early stage of the SCHEIL simulation. It is also found that the solidification paths simulated under the SCHEIL condition have the same two additional solidification steps to those under the lever-rule condition for all four alloys. These two stages are L+Nb3Si+C14+(Nb) and L+Ti5Si3+C14+(Nb). There were trace amounts of fine microstructure that may be corresponded to these two stages. Further detail analysis is needed to identify the phases in the fine microstructure.
For the Nb-10Cr-23Ti-15Si alloy, the predicted primary phase in Fig.4(a) was Nb5Si3, but the microstructure in Fig.4(e) suggests that the primary solidification phase was (Nb). On examination of the isopleths in Fig.3(b), the Si content of the two-phase trough of (Nb)+Nb5Si3 was 14.3%. The nominal alloy composition was located very close to the composition of the eutectic valley. Slight deviation from the nominal composition during sample preparation may be caused by this discrepancy. Both the SCHEIL and the lever-rule models predict the appearance of the large amount of two-phase Nb5Si3+(Nb) eutectic type microstructure, which is in good agreement with the experimental observations.
Figs.4(b) and (f) show that the predicted primary solidification phase for Nb-11Cr-23Ti-13Si was (Nb), which agrees with the experimental observation. The major constituent of the microstructure of the Nb-11Cr-23Ti-13Si alloy was also the two-phase Nb5Si3+(Nb) solidification product.
The predicted primary phase for both the Nb-21Cr-23.5Ti-15.5Si (Fig.4(c)) and the Nb-21Cr-28Ti- 13Si alloys (Fig.4(d)) is Nb5Si3. This suggests that the Si content of the two-phase Nb5Si3+(Nb) valley is shifted to less than 13% when a large amount of Ti and Cr is added. The major difference between Nb-21Cr-23.5Ti-15.5Si and Nb-10Cr-23Ti-15Si is the much higher fraction of C14 phase in the latter alloy, which indicates that the Cr promotes the formation of C14 phase. Both the Scheil and lever-rule models predict that the solidification paths of the two alloys with 21% Cr are L+Nb5Si3, L+Nb5Si3+C14, and L+Nb5Si3+C14+(Nb). The comparison of the as-cast microstructures in Figs.4(g) and (h) suggests that the simulation is in good agreement with experimental observation.
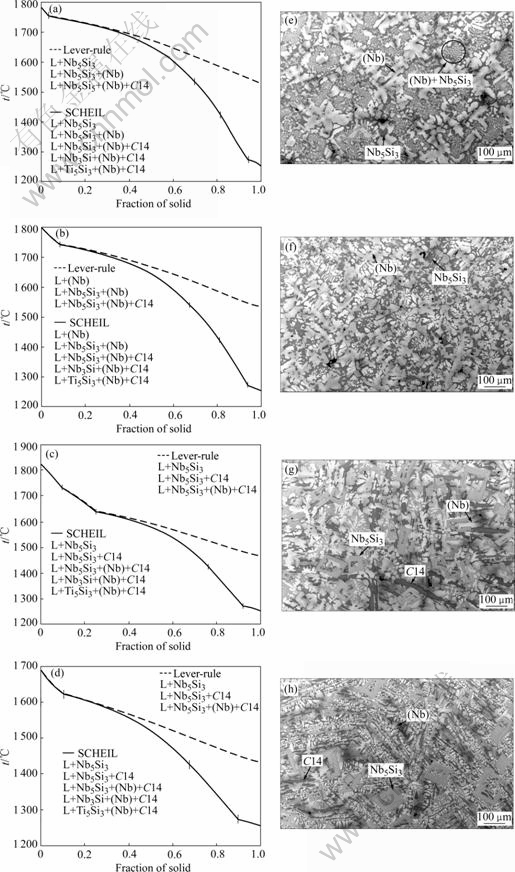
Fig.4 Solidification path simulations for alloys Nb-10Cr-23Ti-15Si (a), Nb-11Cr-23Ti-13Si (b), Nb-21Cr-23.5Ti-15.5Si (c), and Nb-21Cr-28Ti-13Si (d); and BSE images of as-cast microstructure for alloys Nb-10Cr-23Ti-15Si (e), Nb-11Cr-23Ti-13Si (f), Nb-21Cr-23.5Ti-15.5Si (g), and Nb-21Cr-28Ti-13Si (h)
3 Quaternary Mo-Si-B-Ti
The details on/of the thermodynamic modeling and experimental investigations on the quaternary system have been published elsewhere[20]. In this section, a brief description of the thermodynamic modeling and experimental procedure is described first, and then the details on the experimental validation of the 1 600 and 1 200 ℃ solid state-phase equilibria of the Mo-rich phase equilibria are presented. The work reported here provides additional information to corroborate the previously published work[20].
3.1 Thermodynamic modeling
Fig.5 shows a schematic isothermal tetrahedron of the Mo-Si-B-Ti system at 1 600 ℃, focusing on the phase equilibria in the (Mo)-rich region of this quaternary system[20]. The intermetallic phases of interest in this region are Mo3Si(A15), Mo5Si3(T1), Mo2B, MoB, Mo5SiB2(T2) and Ti5Si3(D88). The T1 phase is stable in the Mo-Si-B system, but it is unstable in the Ti-Si-B system, as shown in Fig.5. However, Ti can substitute Mo in the T1-Mo5Si3 phase up to 40% at 1 600 ℃[20]. Similarly, the Mo in A15-Mo3Si phase can be substituted by Ti up to 30%, even though the A15-Mo3Si is not a stable phase in the Ti-Si-B system[20]. In both of these phases, the Si content is not affected by the addition of Ti. This information suggests that substitution between Mo and Ti can also occur in the Mo5SiB2 phase (T2). Therefore, the thermodynamic model of the (Mo,Ti)5(Si)(B)2 was selected to describe the T2 phase. A Gibbs energy was first estimated for “T2-Ti5SiB2”, and then a thermodynamic description was obtained for the T2 phase assuming ideal mixing of Mo and Ti on the sublattices. Models for all the other phases were obtained by extrapolation in a similar manner to that used for the Nb-Cr-Ti-Si system. Thus a preliminary thermodynamic description was developed for the quaternary Mo-Si-B-Ti system, and using this description, the phase equilibria were calculated between the (Mo), A15, T1, D88 and T2 phases, as shown in Fig.5. On the basis of the calculated phase equilibria, selected alloy compositions were identified for experimental investigation. The experimental results were then used to validate and improve the preliminary thermodynamic description.
All of the starting materials used in this work were high purity elements: 99.95% Mo foil, 99.9999% Si lumps, 99.95% B crystals and 99.995% Ti crystals. Button-shaped ingots (6-10 g) were prepared by arc melting in a water-cooled copper crucible in an ultrahigh purity argon atmosphere (99.998% Ar). Samples for heat treatment were annealed at 1 600 ℃ for 150 h and 1 200 ℃ for 50 d in an ultrahigh-purity argon atmosphere (99.998% Ar), followed by furnace cooling to room temperature.
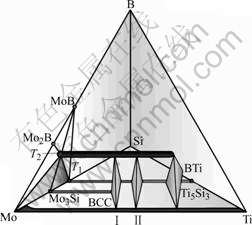
Fig.5 Schematic tetrahedron displaying phase relationships among BCC(Mo), T2, Mo3Si, Mo5Si3(T1) and Ti5Si3 (D88) on metal-rich side of Mo-Si-B-Ti quaternary system at 1 600 ℃
The microstructure of each sample was subjected to similar analyses to those used for the Nb-Cr-Ti-Si alloys. It should be noted that in order to minimize the absorption correction for the light element B, the EPMA analysis was carried out on the uncoated specimens at 7 kV and a beam current of 30 nA, which resulted in decreased electron penetration and X-ray generation closer to the sample surface. The interference between the first order Mo Mg line with the first order B Kα line was resolved through a correction procedure developed by SNETSINGER et al[21] in 1968. This procedure has been successfully used in analyzing the alloys in the Mo-Si-B system[22].
3.2 Results and discussion
This section will focus on the solid-state phase equilibria in the Mo-rich region of the Mo-Si-B-Ti system at 1 600 and 1 200 ℃. Fig.6 shows the calculated 1 600 and 1 200 ℃ isothermal sections with B content of 9%. Only the phase equilibria at the Mo-rich region are labeled. Both isothermal sections show the existence of two four-phase equilibria at the Mo rich region: (Mo)+A15+T2+T1(Ⅰ), and (Mo)+T2+ T1+D88(Ⅱ). From the Mo-Si-B ternary to the four-phase equilibria (Ⅰ), there are two three-phase equilibria: (Mo)+A15+T2 and A15+T1+T2. Between (Mo)+A15+ T2+T1(Ⅰ) and BCC+T2+T1+D88(Ⅱ), there is one three-phase region: (Mo)+T2+T1. At a higher Ti content immediately beyond the four-phase equilibria (Ⅱ), there is another three-phase region (Mo)+T2+D88. Isothermal section at 1 200 ℃ shows a similar topology at the Mo-rich region except that the (Mo)+T2+T1 phase equilibrium is more stable at 1 200 ℃ than that at 1 600℃. Extensive experimental validation has been conducted for the calculated phase equilibria[20].
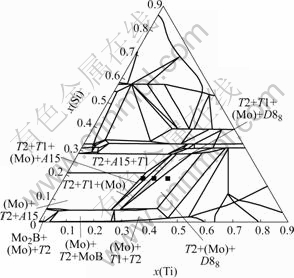
Fig.6 Calculated isothermal sections of Mo-Si-B-Ti system with x(B)=9% at 1 600 ℃
In this section, three alloys were used as examples to demonstrate the comparisons between the calculations and the experiments. They are Mo-18Si-9B-28.5Ti, Mo-18Si-9B-32.5Ti, and Mo-18Si-9B-37.5Ti. As shown in Fig.6, the first two alloys are located in the two four-phase fields: (Mo)+A15+T2+T1 (Ⅰ) and (Mo)+T2+ T1+D88 (Ⅱ), respectively. These two four-phase equilibria are critical to define the range of Ti content in the (Mo)+A15+T2 and the (Mo)+T1+T2 phase fields. Comparisons between the observed microstructures and the calculated phases for these three alloys are presented in Figs.7-9. Each figure has two BSE images from the experiments and one plot of phase fraction vs temperature from the calculations. It should be noted that the calculated phase fraction is the mole fraction but the experimental one is the area fraction. Therefore, the comparison in this regard is qualitative. The two BSE images in each figure correspond to the annealed microstructures at 1 600 ℃ for 150 h and 1 200 ℃ for 50 d, respectively.
Figs.7(a) and (b) show the BSE images of Mo-18Si-9B-28.5Ti annealed at 1 600 and 1 200 ℃, respectively. At 1 600 ℃, this alloy consists of four phases: (Mo), A15, T2, and T1. (Mo) was the white phase, the A15 was light gray phase, the T2 was the medium gray phase, and the T1 was the dark gray phase. At 1 200℃, this alloy has only (Mo), T2, and T1 phases. (Mo) was the white phase, T2 was the light gray phase, and T1 was dark gray phase. A trace amount of the dark phase D88 was found in both images. It is probably the residual product from the segregation during solidification. The calculated plot in Fig.7(c) clearly demonstrates that the Mo-18Si-9B-28.5Ti alloy experiences a phase transformation from the four-phase equilibria (Mo)+T2+ A15+T1 to (Mo)+T2+T1 at temperatures around 1 480 ℃. Both the calculated and experimental results found that the A15 phase is not as stable at low temperatures as that at high temperatures.
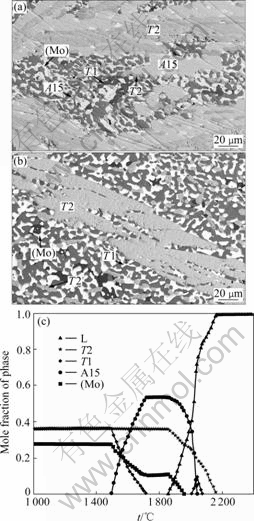
Fig.7 BSE images for Mo-18Si-9B-28.5Ti alloy at 1 600 ℃(a) and 1 200 ℃(b) and phase fraction vs temperature (c)
The BSE images of the Mo-18Si-9B-32.5Ti alloy annealed at 1 600 and 1 200 ℃ are shown in Figs.8(a) and (b), respectively. Both images display four phases: (Mo) was the white phase, T2 was light gray phase, T1 was the dark gray phase, and D88 was the dark phase. The crystal structure of each phase was confirmed by EBSD analysis. The calculation in Fig.8(c) also
Fig.8 BSE images for Mo-18Si-9B-32.5Ti alloy at 1 600 ℃(a) and 1 200 ℃ (b) and phase fraction vs temperature (c)
indicates that this alloy composition is located inside the four-phase field of (Mo)+T2+T1+D88 at both 1 600 and 1 200 ℃. According to the phase rule, the tetrahedron of the four-phase equilibria for a quaternary system at 1 600℃ is fixed. The tetrahedrons of the four-phase equilibria of (Mo)+T2+T1+A15 and (Mo)+T2+T1+D88 at 1 600 ℃ have been well defined through the experimental measurements and thermodynamic calculation. Now these two tetrahedrals have been defined, the range of the Ti content in the two three-phase regions of (Mo)+T2+A15 and (Mo)+T2+T1 have also been defined.
Figs.9(a) and (b) show the microstructure of the Mo-18Si-9B-37.5Ti alloy at 1 600 and 1 200 ℃, respectively. Both images show three-phase contrast: (Mo) in white, T2 in gray, and D88 in dark. This alloy is located in the same phase region at both 1 600 and 1 200℃. The calculated plot of phase fraction vs temperature in Fig.9(c) agrees with the micrographs.
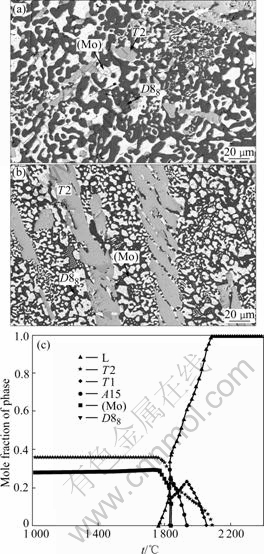
Fig.9 BSE images for Mo-18Si-9B-37.5Ti alloy at 1 600 ℃ (a) and 1 200 ℃ (b) and phase fraction vs temperature (c)
4 Summary
1) The phase diagrams in the metal-rich regions of multicomponent Nb-Cr-Ti-Si and Mo-Si-B-Ti are rapidly established using the Calphad approach coupled with key experiments. The calculated isotherms, isopleths, and solidification paths are validated by experimental work. The solid-state phase equilibria at the Nb-rich region of the Nb-Cr-Ti-Si system at 1 350 ℃ possess a two-phase Nb5Si3+(Nb) field at low Cr content, and a three-phase Nb5Si3+(Nb)+C14 field at high Cr content. The liquid-solid phase equilibria in this region are featured by the primary solidification (Nb) and Nb5Si3, as well as the eutectic formation of (Nb)+Nb5Si3. Cr addition to the Nb-Ti-Si system promotes the formation of the eutectic of Nb5Si3+(Nb).
2) The phase relationships between (Mo), A15, T1, T2 and D88 at 1 600 and 1 200 ℃ are featured by three three-phase equilibria (Mo)+A15+T2, (Mo)+T2+T1 and (Mo)+T2+D88 and two four-phase equilibria (Mo)+T2+T1+A15 and (Mo)+T2+T1+D88. The large substitution of Mo by Ti in the (Mo), T1 and T2 phases results in three-phase (Mo)+T1+T2 phase equilibria in the Mo-Si-B-Ti system, which is not possible in the Mo-Si-B system.
Acknowledgement
The authors would like to thank D J. Dalpe for the directional solidification experiments and Dr. D. A. Wark of R.P.I. for the EMPA measurements for the Nb-Cr-Ti-Si alloys. The authors YANG Ying and Y.A. CHANG would like to thank Doug Berczik and James Myers of Pratt-Whitney for their interest in the work of Mo-Si-B-Ti through the research program of the Revolutionary High Pressure Turbine Blade Material Program of AFRL/ML (Contract No. F33615-98-C-2874). The author YANG Ying would like to thank Dr. Lizhen Tan for the sample fabrication and EBSD measurements of the Mo-Si-B-Ti alloys.
REFERENCES
[1] BEWLAY B P, JACKSON M R, ZHAO J C, SUBRAMANIAN P R. A review of very-high-temperature Nb-silicide-based composites [J]. Metallurgical and Materials Transactions A: Physical Metallurgy and Materials Science, 2003, 34A(10): 2043-2052.
[2] BEWLAY B P, JACKSON M R, ZHAO J C, SUBRAMANIAN P R, MENDIRATTA M G, LEWANDOWSKI J J. Ultrahigh-temperature Nb-silicide-based composites [J]. MRS Bulletin, 2003, 28(9): 646-653.
[3] DIAIDUK D M, PEREPEZK O J H. Mo-Si-B alloys: Developing a revolutionary turbine-engine material [J]. MRS Bulletin, 2003, 28(9): 639-645.
[4] BEWLAY B P, JACKSON M R, LIPSITT H A. The balance of mechanical and environmental properties of a multi-element niobium-niobium silicide-based in situ composite [J]. Metallurgical and Materials Transactions A: Physical Metallurgy and Materials Science, 1996, 27A(12): 3801-3808.
[5] BEWLAY B P, JACKSON M R, SUBRAMANIAN P R. Processing high-temperature refractory-metal silicide in-situ composites [J]. JOM, 1999, 51(4): 32-36.
[6] JACKSON M R, BEWLAY B P, ROWE R G, SKELLY D W, LIPSITT H A. High-temperature refractory metal-intermetallic composites [J]. JOM, 1996, 48(1): 39-44.
[7] MENDIRATTA M G, LEWANDOWSKI J J, DIMIDUK D M. Strength and ductile-phase toughening in the two-phase niobium/niobium silicide (Nb5Si3) alloys [J]. Metallurgical Transactions A: Physical Metallurgy and Materials Science, 1991, 22A(7): 1573-1583.
[8] BERCZIK D M. Oxidation-resistant molybdenum alloys and composites with boron and silicon for dispersed phases. US 9622402 [P], 1996.
[9] SAKIDJA R, PEREPEZKO J H. Alloying and microstructure stability in the high-temperature Mo-Si-B system [J]. Journal of Nuclear Materials, 2007, 366(3): 407-416.
[10] SCHNEIBEL J H, RITCHIE R O, KRUZIC J J, TORTORELLI P F. Optimizaton of Mo-Si-B intermetallic alloys [J]. Metallurgical and Materials Transactions A: Physical Metallurgy and Materials Science, 2005, 36A(3): 525-531.
[11] CHANG Y A, CHEN S, ZHANG F, YAN X, XIE F, SCHMID-FETZER R, OATES W A. Phase diagram calculation: Past, present and future [J]. Progress in Materials Science, 2004, 49(3/4): 313-345.
[12] KAUFMAN L, UHRENIUS B, BIRNIE D, TAYLOR K. Coupled pair potential, thermochemical and phase diagram data for transition metal binary systems (VII) [J]. CALPHAD: Computer Coupling of Phase Diagrams and Thermochemistry, 1984, 8(1): 25-66.
[13] MUGGIANU Y M, GAMBINO M, BROS J P. Enthalpies of formation of liquid alloys bismuth-gallium-tin at 723 K: Choice of an analytical representation of integral and partial excess functions of mixing [J]. Journal de Chimie Physique et de Physico-Chimie Biologique, 1975, 72(1): 83-88.
[14] YANG Y, CHANG Y A, ZHAO J C, BEWLAY B P. Thermodynamic modeling of the Nb-Hf-Si ternary system [J]. Intermetallics, 2003, 11(5): 407-415.
[15] SEIFERT H J, LUKAS H L, PETZOW G. Thermodynamic optimization of the Ti-Si system [J]. Zeitschrift fuer Metallkunde, 1996. 87(1): 2-13.
[16] BEWLAY B P, YANG Y, CASEY R L, JACKSON M R, CHANG Y A. Effect of Cr addition on the phase equilibria of the Nb-Si system [C]// Materials Research Society Symposium Proceedings. Boston, 2007: 333-338.
[17] DU Y, SCHUSTER J C. Experimental investigation and thermodynamic description of the Cr-Si-Ti system [J]. Scandinavian Journal of Metallurgy, 2002, 31(1): 25-33.
[18] CHEN S L, DANIEL S, ZHANG F, CHANG Y A, YAN X Y, XIE F Y, SCHMID-FETZER R, OATES W A. The PANDAT software package and its applications [J]. CALPHAD: Computer Coupling of Phase Diagrams and Thermochemistry, 2002, 26(2): 175-188.
[19] SCHEIL E. Unbroken series of solid solutions in the binary systems of the elements [J]. Zeitschrift fuer Metallkunde, 1942, 34: 242-246.
[20] YANG Y, CHANG Y A, TAN L, CAO W. Multiphase equilibria in the metal-rich region of the Mo-Ti-Si-B system: Thermodynamic prediction and experimental validation [J]. Acta Materialia, 2005, 53(6): 1711-1720.
[21] SNETSINGER K G, BUNCH T E, KEIL K. Electron microprobe analysis of vanadium in the presence of titanium [J]. American Mineralogist, 1968, 53: 1771-1774.
[22] PEREPEZKO J H, SAKIDJA R, KIM S. Phase stability in processing and microstructure control in high temperature Mo-Si-B alloys [C]// Materials Research Society Symposium Proceedings. Boston, 2001: N45.1-N45.12.
(Edited by YANG Bing)
Corresponding author: YANG Ying; Tel: +1-608-274-1414; E-mail: Ying.Yang@computherm.com
