


Trans. Nonferrous Met. Soc. China 22(2012) 2220-2225
Nonlinear elastic deformation of magnesium and cobalt by Preisach-Mayergoyz model
LI Liang, WANG Hong-ying, ZHOU Ai-guo
School of Materials Science and Engineering, Henan Polytechnic University, Jiaozuo 454100, China
Received 27 September 2011; accepted 4 May 2012
Abstract: A classic hysteretic model, Preisach-Mayergoyz model (P-M model), was used to calculate the nonlinear elastic deformation of magnesium (Mg) and cobalt (Co). Mg and Co samples in cylinder shape were compressively tested by uniaxial test machine to obtain their stress—strain curves with hysteretic loops. The hysteretic loops do have two properties of P-M hysteretic systems: wiping out and congruency. It is proved that P-M model is applicable for the analysis of these two metals’ hysteresis. This model was applied on Mg at room temperature and Co at 300 ℃. By the P-M model, Co and Mg nonlinear elastic deformation can be calculated based on the stress history. The simulated stress—strain curves agree well with the experimental results. Therefore, the mechanical hysteresis of these two metals can be easily predicted by the classic P-M hysteretic model.
Key words: magnesium; cobalt; nonlinear elastic deformation; Preisach-Mayergoyz model
1 Introduction
Magnesium and cobalt have a hexagonal closed packed (HCP) crystal structure. Compared with face centered cubic closed packed (FCC) metals, HCP metals do not have five independent slip systems and their ductility is not good. If these metals are loaded by a stress near their elastic limits, primary dislocations start to glide and the metals start plastic deformation by slipping. However, due to the anisotropy of HCP structures, secondary dislocations are not moveable because the applied stress is not high enough. At this situation, only the dislocations in the primary slip planes are moveable and cannot be entangled with each other. If the applied stress decreases, the dislocations move back due to the attractive force between dislocations, and deformation recovers partially. If the applied stress increases continually, the metals deform by secondary slipping, twinning or kink bands.
Only primary slipping cannot result macro-yielding but micro-yielding [1]. Micro-yielding makes the samples more deform than the linear elastic deformation according to Hook’s law. If the applied stress is removed, this deformation can recover. Thus it is defined as nonlinear elastic deformation. Due to this deformation, the load curves and unload curves at the stress—strain curve figure are not superimposed. Hysteretic loops are generated. The stress—strain curves with hysteretic loops of Mg were reported in Refs. [2-4]. And recently, it was also reported that stress—strain curves of Co have similar hysteretic loops [3,5,6].
This mechanical behavior of Mg and Co is actually mechanical hysteresis. Hysteresis is a ubiquitous phenomenon [7]. The most studied hysteresis is ferromagnetic hysteresis. The mechanical hysteresis of grainy solids and rocks was noted and studied [8,9]. Mechanical hysteresis of Mg and Co is different from that of rocks because these metals have a perfect crystal structure and the hysteresis is because of the dislocation motion inside solid grains. Two mechanisms (reversible twins [4,10-12] and incipient kink bands [2,3,5]) were proposed respectively as the physical origin of this hysteresis. By these mechanisms, the influence of porosity, texture or impurity on the deformation was understood. Those works are important for the controlling of the deformation.
It was noted that the nonlinear elastic deformation is similar to anelasticity of metals with HCP structure [13,14] , which was extensively researched. Even ice has similar anelasticity [15-17]. Actually anelasticity and nonlinear elasticity are same mechanical behaviors. The difference is that anelasticity emphasizes the extra relaxation of deformation during unloading while nonlinear elasticity emphasizes extra deformation during loading. Dislocations, point defects and grain boundary sliding were proposed as the reasons of anelasticity [13,15-17], similar with the reasons of nonlinear elasticity of metals.
However, no matter what are the physical reasons of the nonlinear elasticity (mechanical hysteresis), can people find a simple way to predict the mechanical hysteresis? In other words, is there a simple mathematic method to simulate stress—strain curves of Mg and Co with hysteresis loops?
2 P-M model
Following the lead of the geologists[Guyer, 1999 #223;Guyer, 1997 #294], Preisach model is a possible method to do this simulation. First to describe the ferromagnetic hysteresis [18], the Preisach model was based on the idea that macroscopically observed hysteresis can be decomposed into independent hysteretic operators described by independent bi-stable relays. MAYERGOYZ [19,20] recognized that the Preisach model offered a general mathematical framework for the description of hysteresis of different physical origins, and derived the necessary and sufficient conditions for representation of any given hysteresis by the Preisach model. These conditions are: first, each local input maximum wipes out the effect of input below it, and second, the hysteresis loops obtained via cycles with the same end points of input, but different pre-histories are congruent. He called these properties as wiping out and congruency, respectively. Thereafter, the Preisach model was renamed as the Preisach-Mayergoyz or P-M model.
In the mathematical P-M model, the state of a material system is determined by the collection operators 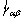 with rectangular hysteresis loops (Fig. 1) [6,19]. The output strain of each
with rectangular hysteresis loops (Fig. 1) [6,19]. The output strain of each 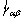 can only be 0 or 1. Every
can only be 0 or 1. Every 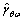 has one up-threshold stress θ and one down-threshold stress ω(θ>ω>0). For loading from 0,
has one up-threshold stress θ and one down-threshold stress ω(θ>ω>0). For loading from 0, 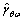 =0 if σ<θ. If σ≥ω, then
=0 if σ<θ. If σ≥ω, then 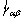 =1. During unloading,
=1. During unloading, 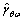 =1 if σ>ω and
=1 if σ>ω and 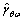 =0 if σ≤ω. If the contribution of operator
=0 if σ≤ω. If the contribution of operator 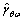 to the overall strain is μ(θ, ω), which is called P-M density, then the output strain of whole system after a given load history is the sum of the outputs of all
to the overall strain is μ(θ, ω), which is called P-M density, then the output strain of whole system after a given load history is the sum of the outputs of all 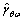 weighed by μ(θ, ω) or [6,19]:
weighed by μ(θ, ω) or [6,19]:
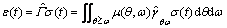 (1)
(1)
where ε(t) can be calculated by double integration if μ(θ,ω) is known. μ(θ,ω) can be obtained by double differentiation of the experimentally obtained first-order reversal curves. However, it is not necessary to actually differentiate experimental data and then carry out integration to obtain ε(t). One can define an auxiliary function known as Everett function related directly to differences of ε(t) obtained at σ(t) along different reversal curves. All calculations of the output of the P-M model can be carried out only on the basis of this Everett function [6,19].
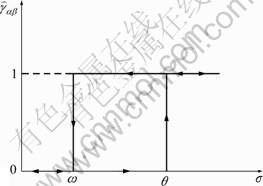
Fig. 1 Rectangular hysteretic loop of P-M model
A simple calculation can be carried out if one follows the algorithm proposed in Ref. [19], which uses parametric fitting involving just summation and subtraction of typical experimental results such as nested stress-strain loops. This approximate method permits a relatively simple graphical construction of the Preisach space distribution function (P-M density) and can be used for the simulation of any arbitrary stress-strain relationship.
We mentioned the idea to do P-M model analysis on the nonlinear elastic deformation of some ceramics such as ternary carbide [21] and hexagonal boron nitride [22]. In Ref. [6], we gave the mathematic derivation and analysis in details on the deformation of some ceramics and metal Co. All the experiments were done at room temperature. Similar with these materials, Mg has the same hexagonal structure and is very famous for its high damping capacity. Therefore, it is of great significance to do similar analysis on Mg. This is the main objective of this work. Another objective is to know whether this model is effective at a high temperature of 300 ℃.
3 Experimental
Mg (>99% purity) ingots tested in this work were from Huanghe Magnesium Alloys Co., Ltd., Jiaozuo, China. Cobalt (99.97% purity) rods were from ESPI metals, Ashland, Oregon, USA. Mg ingots were directly electro-discharge machined to cylinders with the diameter of 20 mm and length of 60 mm. Co rods were annealed at 1000 ℃ in argon atmosphere for 4 h before electro-dischage cutting to cylinders with the diameter of 12.7 mm and length of 31 mm.
Mg cylinders were compressively tested by a servo-controlled testing system (RMT-150B) from Wuhan Institute of Rock and Soil Mechanics, the Chinese Academy of Sciences. Both the loading and unloading rates were 2 N/s (6.4 kPa/s). The deformation was measured by a displacement sensor with full scale of 5 mm. The sensor measured the distance change between the top and bottom punches holding the samples. Co cylinders were compressively tested by a hydraulic testing machine (MTS 810, Minneapolis, Minnesota, USA), supplied with a controller (Microconsoler 458.20, MTS). An extensometer (MTS 632.59C-01) attached directly to the sample was used to measure the strains.
4 Results and discussion
A Mg sample was polished and chemicaly etached (v(FeCl3):v(H2O)=1:20) to reveal its microstructure. The optical micrograph is shown in Fig. 2. The grain size is (500±80) μm. The grain at the top-right corner shows obvious primary slipping lines. Co samples after annealling have a similar microstructure while the grain size is (110±30) μm.

Fig. 2 Optical micrograph of Mg sample
Typical compressive stress—strain curves of Mg are shown in Fig. 3(a). At a low stress (<10 MPa), the response is linear elastic, with a slope corresponding to the elastic modulus, E. If the stress is higher than the yield strength (10 MPa), some plastic deformation was observed with strain hardening. If the sample was unloaded to 0 MPa then loaded to the same stress level, hysteresis loops with a little plastic deformation were observed. If this cycle was repeated several times, the loops became more and more closed. A fully closed hystetetic loops could be obtianed finally.
The stress—strain curves of Co is shown in Fig. 3(b). The Co sample was first loaded to 230 MPa and unloaded to 0 MPa. Then it was loaded to a progressive lower stress-level and then fully unloaded. Every load-unloaded cycle obtained a fully closed hysteretic loop. After 9 cycles, the stress—strain curves with nested hysteretic loops were obtained as shown in Fig. 3(b).
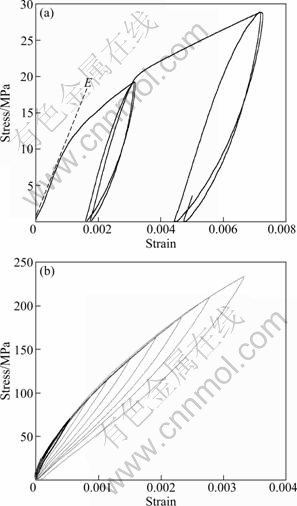
Fig. 3 Compressive stress—strain curves of Mg (a) and Co (b)
In order to use P-M model to simulate stress—strain curves of Mg and Co with hysteretic loops, it is needed to verify that these hysteretic loops have two properties: wiping out and congruency. This was done by the plots in Fig. 4. Figure 4(a) shows two minor loops of stress—strain curves of Mg. The inset is the whole main hysteretic loop including the two minor loops. From Fig. 4(a), it is clear that both minor loops are fully closed and do not change the continuity of main loop. This verifies the wiping out property of this hysteresis. And the two minor loops with the same maximum stress and minimum stress have congruent shape no matter that one attachs to load curve and the other attachs to unload curve. This verifies the congruency property. Figure 4(b) shows the similar stress—stain curves of Co. Moreover, the experiment for Co was done at 300 oC. Therefore, it can be concluded that the mechanical hysteresis of Mg and Co has wiping and congruency properties at room temperature and even at a high temperature. And the mechanical hysteresis of these two metals can be analyzed by P-M model.
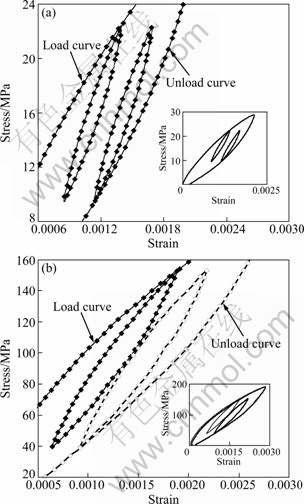
Fig. 4 Two minor loops attached to load curve or unloade curve respectively for Mg at room temperature (a) and Co at 300 ℃ (b)
If a sample such as Mg or Co is compressed by a stress change with time, the strain of this sample is also changeable with time. Due to a nonlinear elastic deformation, the strain does not only depend on the stress at the moment. All stress values before that moment, namely stress history, control the strain of this sample at the moment. This strain can be measured by extensometer or stain sensor. However, it also can be calcualted from stress history by Eq. (1) if P-M density, μ(θ,ω), is known. P-M density can be obtained from nested stress—strain hysteretic loops such as Fig. 3(b). The method for obtaining P-M density from the nested loops was described in details at previous papers [6,19]. The P-M density of Mg is shown in Fig. 5. The areas with dark colour mean low P-M density while light colour areas mean high P-M density. A small strip area near the bottom line has the most light colour and the highest P-M density. This sugests that, inside the Mg samples, there are many hysteretic operators with down threshold stress ω near 0 and variable up threshold stress θ. This is different from the previous reported P-M density distribution of ceramics and Co [6], while the highest density roughly falls on a 45° line. Therefore, compared with other materials, Mg can have mechanical hysteresis at a pretty low stress and the hysteretic loops are easily detected. This can explain why Mg is so well-known for its high damping capacity and stresss—strain hysteretic loops.
Figure 6 gives an example of the measured results and calculated results for Mg and Co. Besides measure experiment, the strains of Mg and Co can be calculated from the P-M density obtained from the experimental result. Figure 6(a) shows the measured and calculated stress vs strain plots of Mg. The strain was continuely measured. And true stress—strain curves with hysteretic loops (solid curves in Fig. 6(a)) were obtained. By the P-M model in section 2, the strains corresponding to stress can be calculated, which are symbled by diamonds in the plot. From the figure, calculated strains (diamonds) agree well with the measured strains (solid curve). Figure 5(b) shows the similar agreement of Co by stress vs time and strain vs time plots. A Co sample was tested by a stress change with time as shown by a dash curve in the figure. The measured strain change with time is shown by a solid curve. At 36 different moments, the strains were calculated by P-M model based on stress history and were symboled by diamonds in Fig. 6(b). A good agreement betwent measured and calcualted strains is obvious.

Fig. 5 P-M density distribution of Mg
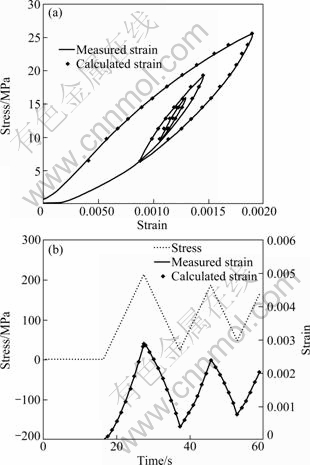
Fig. 6 Experimentally measured strain and calculated strain change with stress or time: (a) Mg; (b) Co
5 Conclusions
1) From the experimental results, it is the first time to show that the mechanical hysteresis of Mg at room temperature and that of Co at 300 ℃ has wiping out and congruency properties. These two properties are sufficient and necessary conditions for a hysteresis system to be a Presiach hysteresis.
2) It was verified that stress—strain curves of Mg and Co with hysteretic loops can be simulated by P-M model. The simulated curves agree well with the experimental results.
3) From the point of view of P-M model, beasue of the high densty of hysteretic operators with very low threshold stress, the hysteretic loops at stress—strain curves of Mg are so obvious.
4) The mechanical hysteresis of these two metals can be easily predicted by P-M hysteretic model.
References
[1] YOO M H, WEI C T. Slip modes of hexagonal-close-packed metals [J]. Journal of Applied Physics, 1967, 38(11): 4317-4322.
[2] ZHOU A G, BARSOUM M W. Kinking nonlinear elasticity and the deformation of magnesium [J]. Metallurgical and Materials Transactions A, 2009, 40(7): 1741-1756.
[3] ZHOU A G, BASU S, BARSOUM M W. Kinking nonlinear elasticity, damping and microyielding of hexagonal close-packed metals [J]. Acta Materialia, 2008, 56(1): 60-67.
[4] MANN G E, SUMITOMO T, CACERES C H, GRIFFITHS J R. Reversible plastic strain during cyclic loading-unloading of Mg and Mg-Zn alloys [J]. Materials Science and Engineering A, 2007, 456(1-2): 138-146.
[5] ZHOU A G, BROWN D, VOGEL S, YEHESKEL O, BARSOUM M W. On the kinking nonlinear elastic deformation of cobalt [J]. Materials Science and Engineering A, 2010, 527(18-19): 4664-4673.
[6] ZHOU A G, BASU S, FRIEDMAN G, FINKEL P, YEHESKEL O, BARSOUM M W. Hysteresis in kinking nonlinear elastic solids and the Preisach-Mayergoyz model [J]. Physical Review B, 2010, 82(9): 094105.
[7] MAYERGOYZ I D. Mathematical-models of hysteresis [J]. Physical Review Letters, 1986, 56(15): 1518-1521.
[8] NIHEI K T, HILBERT L B, COOK N G W, NAKAGAWA S, MYER L R. Frictional effects on the volumetric strain of sandstone [J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(1-2): 121-132.
[9] GUYER R A, TENCATE J, JOHNSON P. Hysteresis and the dynamic elasticity of consolidated granular materials [J]. Physical Review Letters, 1999, 82(16): 3280-3283.
[10] REED-HILL R E, DAHLBERG E P, SLIPPY W A. Some anelastic effects in zirconium at room temperature resulting from prestrain at 77 ℃ [J]. Transactions of the Metallurgical Society of AIME, 1965, 233: 1766-1771.
[11] WU L, JAIN A, BROWN D W, STOICA G, AGNEW S R, CLAUSEN B, FIELDEN D, LIAW P. Twinning-detwinning behavior during the strain-controlled low-cycle fatigue testing of a wrought magnesium alloy, ZK60A [J]. Acta Materialia, 2008, 56(4): 688-695.
[12] BROWN D W, JAIN A, AGNEW S R, CLAUSEN B. Twinning and detwinning during cyclic deformation of Mg alloy AZ31B [J]. Materials Science Forum, 2007, 539-543: 3407-3413.
[13] POVOLO F, BISOGNI E A. Anelastic behaviour of isolated point defects in crystals of h.c.p. structure [J]. Acta Metallurgica, 1967, 15(5): 701-706.
[14] NOWICK A. Anelastic effects arising from precipitation in aluminum-zinc alloys [J]. Journal of Applied Physics, 1951, 22(7): 925-933.
[15] DUVAL P, ASHBY M F, ANDERMAN I. Rate-controlling processes in the creep of polycrystalline ice [J]. Journal of Physical Chemistry, 1983, 87(21): 4066-4074.
[16] GOSAR P. Theory of the anelastic relaxation of cubic and hexagonal ice [J]. Philosophical Magazine, 1974, 29(2): 221-240.
[17] COLE D M, DURELL G D. A dislocation-based analysis of strain history effects in ice [J]. Philosophical Magazine A, 2001, 81(7): 1849-1872.
[18] PREISACH F. ?ber die magnetische Nachwirkung [J]. Zeitschrift fur Physik, 1935, 94(5-6): 277-302.
[19] MAYERGOYZ I. Mathematical models of hysteresis and their applications [M]. New York: Academic Press, 2003.
[20] MAYERGOYZ I D. Mathematical models of hysteresis [J]. Physical Review Letters, 1986, 56(15): 1518-1521.
[21] ZHOU A G, BARSOUM M W. Nonlinear elastic deformation of MAX phases [J]. Key Engineering Materials, 2010, 434: 149-153.
[22] ZHOU A G, LI H R. Mechanical hysteresis of hexagonal boron nitride [J]. Journal of Wuhan University of Technology: Mater Sci Ed, 2011, 26(5): 935-938.
Preisach-Mayergoyz模型分析金属镁与钴的非线性弹性变形
李 良,王红英,周爱国
河南理工大学 材料科学与工程学院,焦作 454100
摘 要:应用一个经典滞后模型Preisach-Mayergoyz模型(P-M模型)计算金属镁与钴的非线性弹性变形,模拟这两种金属的应力—应变曲线中的滞后环。分析实验所获取的应力—应变曲线,金属镁和钴的力学滞后具有成为P-M滞后的2个充分必要条件:抹除性和一致性。它们的力学滞后可以应用P-M模型分析。证明了金属镁这种重要的结构材料的非线性弹性变形具有这种特性,钴在300 ℃的高温下具有这种性能。P-M模型提供了一种简单的方法计算这两种金属的非线性弹性变形。模拟计算的结果和实验结果吻合良好。
关键词:镁;钴;非线性弹性变形;Preisach-Mayergoyz模型
(Edited by LI Xiang-qun)
Foundation item: Projects (51002045, 10947105) supported by the National Natural Science Foundation of China? Project (2010B430016) supported by the Nature Science Research Project of Education Department of Henan Province, China? Project (2012IRTSTHN007) supported by Program for Innovative Research Team (in Science and Technology) in the University of Henan Province, China
Corresponding author: ZHOU Ai-guo? Tel: +86-391-3986936; E-mail: zhouag@hpu.edu.cn
DOI: 10.1016/S1003-6326(11)61452-0