混合噪声的各向异性扩散平滑
马捷1,严家斌1, 2,刘贵忠2,柳建新1
(1. 中南大学 信息物理工程学院,湖南 长沙,410083;
2. 西安交通大学 电子与信息工程学院,陕西 西安,710049)
摘 要:针对混合噪声模型中中值滤波、线性滤波与传统各向异性扩散存在固有的缺陷,通过修改扩散项的计算方式改进扩散模型并提高扩散模型的滤波特性,改进模型具有带通滤波特性,扩散过程稳定并满足极值原理。研究结果表明:中值滤波作为一种经典的非线性滤波方法仅适合于“飞点”噪声的滤波并引起图像的角点、线条损失,线性滤波扩大或使图像边界范围模糊;传统的各向异性扩散能对随机噪声有效地压制,但对“飞点”噪声会产生虚假的边缘甚至反扩散,而改进模型既具有中值滤波的特性又具有传统各向异性扩散的性能,适合于平滑不同强度与形状的混合噪声,并对角点、线条、边缘等细节信息提供足够保护。
关键词:混合噪声;各向异性扩散;飞点;边缘
中图分类号:TN911.73 文献标志码:A 文章编号:1672-7207(2010)01-0231-07
Anisotropic diffusion smoothing of mixed noise
MA Jie1, YAN Jia-bin1, 2, LIU Gui-zhong2, LIU Jian-xin1
(1. School of Info-Physics and Geomatics Engineering, Central South University, Changsha 410083, China;
2. School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China)
Abstract: Based on the fact that there is intrinsic drawback for median filter, linear filter and tradition anisotropic diffusion to mixed noise, a new diffusion model was proposed by modifying the calculation method of diffusion term and improving filter capability of the model. The improved model possesses band-pass filer characteristic, diffuses processing stability and satisfies the max-min principle. The simulation results show that the median filter is only proper for outlies noise and removes the thin line and corners of image. The linear filter extends or blurs the boundary of image. The anisotropic diffusion removes random noise effectively, but it brings about illusive edge and back diffusion for outlies noise. The improved model that possesses both median filter characteristics and anisotropic diffusion capability is proper for various mixed noise and can sufficiently protect the detailed characteristic such as corner, thin line and edge.
Key words: mixed noise; anisotropic diffusion; outlies; edge
在图像处理中,均值滤波及其他线性滤波对高斯随机噪声在最小均方误差意义下的滤波效果是最优的,但对于噪声如脉冲或飞点噪声及其他重尾噪声、与信号相关的噪声如斑点噪声的滤波效果较差,同时,还会模糊图像的边界、线条及其他细节信息[1-2]。中值滤波器是1种对飞点噪声稳健、计算方法简单的非线性滤波器,不足之处是会消除图像中的细节如细线条和角点信息。对此,国内外研究者提出了许多改进的中值滤波算法如多级滤波器、堆栈滤波器、加权滤波器、松弛滤波器等[3-7]。松弛滤波器是利用2个参数控制滤波算子的性能,使滤波值在噪声压制和细节保护之间达到某种平衡,与其他滤波器相比,该滤波器更好地压制了高斯噪声和重尾噪声并保护了细节信 息[7]。中值滤波器作为一种选择滤波器,它的输出是输入样本之一,因而,对于飞点噪声,关键在于窗口内样本的统计特性及飞点的判定方法。描述飞点噪声的统计模型有多种,如拉氏模型、柯西模型、 -stable模型[8-9]。
-stable模型[8-9]。 -stable模型是一种模拟混合噪声的数学模型,参数
-stable模型是一种模拟混合噪声的数学模型,参数 控制模型的形状,
控制模型的形状, 越小,模型的脉冲性或飞点性越强;当
越小,模型的脉冲性或飞点性越强;当 =2时,
=2时, -stable模型为典型的高斯模型;当
-stable模型为典型的高斯模型;当 =1时,
=1时, -stable模型为柯西模型;当0<
-stable模型为柯西模型;当0< <2时,
<2时, -stable模型为混合模型[9]。Ben等[10]利用
-stable模型为混合模型[9]。Ben等[10]利用 -stable模型把松弛滤波器和均值滤波结合起来有效地压制了具有重尾特性的混合噪声。考虑到各向异性扩散的定向扩散能力及特点,Ling等[11]在扩散过程中利用中值滤波压制飞点噪声的影响。对于分布模型复杂的噪声,滤波器的选择首先应适合于噪声模型,并保证处理过程的稳健性;其次,在噪声压制与细节信息的保护2个方面达到合理平衡。考虑到在一定条件下Robust估计过程与各向异性扩散过程的等价 性[12-13],虽然各向异性扩散具有对飞点噪声不敏感的特性,但扩散过程可能不稳定并引起反扩散。为此,本文作者改进各向异性扩散模型。这种新的扩散模型具有带通滤波特性和扩散的稳定性,并证明了改进的扩散模型同样满足极值原理。
-stable模型把松弛滤波器和均值滤波结合起来有效地压制了具有重尾特性的混合噪声。考虑到各向异性扩散的定向扩散能力及特点,Ling等[11]在扩散过程中利用中值滤波压制飞点噪声的影响。对于分布模型复杂的噪声,滤波器的选择首先应适合于噪声模型,并保证处理过程的稳健性;其次,在噪声压制与细节信息的保护2个方面达到合理平衡。考虑到在一定条件下Robust估计过程与各向异性扩散过程的等价 性[12-13],虽然各向异性扩散具有对飞点噪声不敏感的特性,但扩散过程可能不稳定并引起反扩散。为此,本文作者改进各向异性扩散模型。这种新的扩散模型具有带通滤波特性和扩散的稳定性,并证明了改进的扩散模型同样满足极值原理。
1 中值滤波
中值滤波是把信号或图像中的灰度用其邻域的中位数来替代。对于1-D离散信号{u1, u2, u3, …, un},按大小进行排序:u1≤u2≤u3≤…≤un,则滤波输出值为:
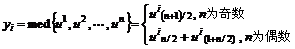
其中:ui表示离散样本值;med表示取中位数。显然,对于2-D离散信号,有:
 (1)
(1)
其中:W为滤波窗口,通常为3×3。
中值滤波作为一种典型的非线性滤波器能有效地消除飞点噪声、椒盐噪声,但若滤波窗口选择不当,则可能会损失一些细节信息[1],中值滤波对角点和细线的影响分别如图1和图2所示。其中:图1(a)所示为图像中某条剖面线的灰度,在位置点6~10之间是灰度为5.00的高值区,背景灰度为1.00;中值滤波后(图1(b)),左右2个角点处的灰度由5.00变为1.00,高值区的范围变小(仅在位置点7~9的灰度为5.00),即损失了2个角点信息。同样,对于图2(a)中所表示的细线信息经中值滤波后被平滑,灰度由5.00变为背景值1.00(图2(b))。因此,中值滤波对于点、线较多的图像信号是不适合的。
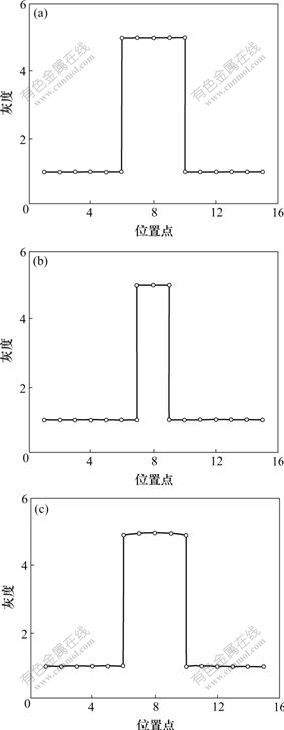
(a) 原始曲线;(b) 中值滤波结果;(c) 改进模型滤波结果
图1 中值滤波对角点的影响
Fig.1 Influence of median filter on corner
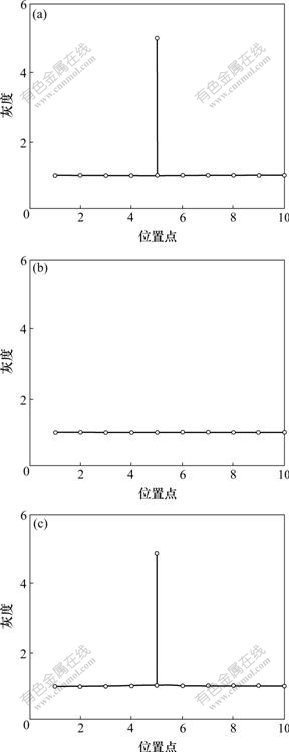
(a) 原始曲线;(b) 中值滤波结果;(c) 改进模型滤波结果
图2 中值滤波对细线的影响
Fig.2 Influence of median filter on thin line
2 各向异性扩散及性能
各向异性扩散(Anisotropic diffusion, AD)是基于局部梯度估计的一种非线性滤波方法,以梯度幅值的降函数作为扩散速度,典型的扩散模型为[13-15]:

其中: 为梯度算子;div为散度算子;u0为初始信号(图像);t为扩散时间尺度;g为扩散系数函数,如:
为梯度算子;div为散度算子;u0为初始信号(图像);t为扩散时间尺度;g为扩散系数函数,如: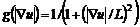 ;L为阈值参数。在图像的边缘或边界区域由于有较大的梯度模,因而g较小,扩散速度较小。若梯度模较小,则g较大,扩散速度 较大。
;L为阈值参数。在图像的边缘或边界区域由于有较大的梯度模,因而g较小,扩散速度较小。若梯度模较小,则g较大,扩散速度 较大。
方程(2)的1-D离散形式可表示为:
 (3)
(3)
其中:K和M为调节参数。L2=M/k, 0<λ=1/M<1/2。当k→∞时,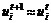 ;
; 时,方程(3)能对信号的高频信息进行适当保护;k=0时扩散方程就退化为(ui-1, ui, ui+1)对称线性滤波方程:
时,方程(3)能对信号的高频信息进行适当保护;k=0时扩散方程就退化为(ui-1, ui, ui+1)对称线性滤波方程:
 (4)
(4)
可见,各向异性扩散与线性滤波器存在一定联系。事实上,对于1-D常系数热传导扩散方程为:
 ,u(x, 0)=u0 (5)
,u(x, 0)=u0 (5)
它的解为:
 (6)
(6)
相应的古典差分式为:
 (7)
(7)
其中:h为离散的网格步长。方程(7)是各向同性扩散方程,其离散形式与(4)式类似。因此,通过调整式(3)中的参数k和M可以改变其滤波特性,如非线性和线性、各向异性与各向同性。
在各向异性扩散中,当梯度估计值大于阈值L时会引起扩散过程不稳定,发生反扩散[16],即 的扩散系数是负数,使得整个扩散过程呈发散状态。重写方程(3)得到梯度估计值与阈值参数L的关系式:
的扩散系数是负数,使得整个扩散过程呈发散状态。重写方程(3)得到梯度估计值与阈值参数L的关系式:

 (8)
(8)
 ,
, 。由于式(8)的分母大于或等于1,令它为B,则
。由于式(8)的分母大于或等于1,令它为B,则
 (9)
(9)
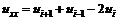 ,为二阶导数的古典差分表达式。若
,为二阶导数的古典差分表达式。若 ,则扩散方程(9)具有负的扩散系数,将发生反扩散行为。因此,在AD扩散过程中应保证有下述关系成立:
,则扩散方程(9)具有负的扩散系数,将发生反扩散行为。因此,在AD扩散过程中应保证有下述关系成立:
 (10)
(10)
否则,会影响扩散的稳定性。
3 扩散模型的改进与噪声的压制
为了增强扩散过程的稳定性,扩散模型修改为:

相对于方程(3),方程(11)具有带通滤波响应特征,有利于压制“飞点”噪声。例如,当 ,且
,且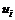 与ui-1和ui+1相比有显著差别时(如“飞点噪声”),
与ui-1和ui+1相比有显著差别时(如“飞点噪声”),
 ,
, (12)
(12)
因此,方程(11)输出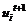 更多地受扩散项的影响,具有中值滤波的特性;当
更多地受扩散项的影响,具有中值滤波的特性;当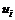 与ui-1和ui+1相比差别较小时(如边界线上),
与ui-1和ui+1相比差别较小时(如边界线上),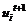 变化主要受式(11)中
变化主要受式(11)中 的影响,而
的影响,而 为中心点的前向差分与后向差分之和,因而,式(11)又具有传统的各向异性扩散的特性。因此,式(11)适合于混合噪声模型的处理。如图3所示,在背景灰度为1.00的剖面中存在1个灰度为2.00的区域,并在左上角有1个异常点即飞点5.00(图3(a));利用改进模型滤波后(图3(b)),飞点灰度得到压制并由5.00变为2.20,同时,保持了高值区的基本形状;而经AD滤波后(图3(c)),飞点依然存在,其灰度为4.14,并使位置点7的灰度(2.00)损失了更多的信息,变为1.83;经中值滤波后(图3(d)),飞点虽然得到压制,使飞点灰度由5.00变为1.00,但损失了角点的信息,使高值区域明显变小。同时,改进模型很好地保护了角点、细线及边缘信息,如图1(c)中角点灰度为4.93,相对于正常值5.00,最大的变化不超过1.5%。对于图像处理中常见的线条,经过处理后其灰度的变化也仅为2%左右(图2(c))。
为中心点的前向差分与后向差分之和,因而,式(11)又具有传统的各向异性扩散的特性。因此,式(11)适合于混合噪声模型的处理。如图3所示,在背景灰度为1.00的剖面中存在1个灰度为2.00的区域,并在左上角有1个异常点即飞点5.00(图3(a));利用改进模型滤波后(图3(b)),飞点灰度得到压制并由5.00变为2.20,同时,保持了高值区的基本形状;而经AD滤波后(图3(c)),飞点依然存在,其灰度为4.14,并使位置点7的灰度(2.00)损失了更多的信息,变为1.83;经中值滤波后(图3(d)),飞点虽然得到压制,使飞点灰度由5.00变为1.00,但损失了角点的信息,使高值区域明显变小。同时,改进模型很好地保护了角点、细线及边缘信息,如图1(c)中角点灰度为4.93,相对于正常值5.00,最大的变化不超过1.5%。对于图像处理中常见的线条,经过处理后其灰度的变化也仅为2%左右(图2(c))。

(a) 原始曲线;(b) 改进模型滤波;(c) AD滤波;(d) 中值滤波
图3 “飞点”噪声平滑的比较
Fig.3 Comparison of outlies noise smoothing
方程(11)可写为:
 (13)
(13)
其中: 。在离散化计算过程中,为保证稳定性,M必须大于或等于2[17],则0<1/C≤0.5,扩散方程(11)不可能有负的扩散系数,即不会有反扩散行为发生,保证了在信号处理过程中不会放大局部干扰。AD滤波、线性滤波和改进模型滤波的性能比较结果如图4所示。由图4(a)可见:灰度呈高低间隔变化的剖面,在位置点6,7和12存在几个会发生反扩散的异常点,其灰度分别为:4.00,2.00和2.00。在各向异性扩散平滑过程中若把扩散点及邻域值代入(10)式中的
。在离散化计算过程中,为保证稳定性,M必须大于或等于2[17],则0<1/C≤0.5,扩散方程(11)不可能有负的扩散系数,即不会有反扩散行为发生,保证了在信号处理过程中不会放大局部干扰。AD滤波、线性滤波和改进模型滤波的性能比较结果如图4所示。由图4(a)可见:灰度呈高低间隔变化的剖面,在位置点6,7和12存在几个会发生反扩散的异常点,其灰度分别为:4.00,2.00和2.00。在各向异性扩散平滑过程中若把扩散点及邻域值代入(10)式中的 进行计算,则会发现在异常点上的灰度分别为2.00,3.00和2.00,都大于L2(即4/3)。因此,在异常点上的灰度会因反扩散而成为4.06,1.94和1.91(图4(b))。随着扩散的不断进行,位置点7和12的灰度不断变小,而位置6的灰度则不断变大并导致扩散过程不稳定,这显然不是所期望的。利用式(4)进行线性滤波后,各异常点得到较好地平滑,其灰度分别为:3.00,3.25和2.75,但它模糊了信号高值区与背景区灰度1.00边界,高值区的边界有可能被扩大(图4(c))。而改进扩散模型(图4(d))扩散中异常点都满足方程式(10),其灰度分别为:3.93,2.07和2.08。随着扩散的进行,不会发生反扩散,在扩散中改进模型滤波后并没有扩大或缩小高值区的边界范围,即没有模糊边界。
进行计算,则会发现在异常点上的灰度分别为2.00,3.00和2.00,都大于L2(即4/3)。因此,在异常点上的灰度会因反扩散而成为4.06,1.94和1.91(图4(b))。随着扩散的不断进行,位置点7和12的灰度不断变小,而位置6的灰度则不断变大并导致扩散过程不稳定,这显然不是所期望的。利用式(4)进行线性滤波后,各异常点得到较好地平滑,其灰度分别为:3.00,3.25和2.75,但它模糊了信号高值区与背景区灰度1.00边界,高值区的边界有可能被扩大(图4(c))。而改进扩散模型(图4(d))扩散中异常点都满足方程式(10),其灰度分别为:3.93,2.07和2.08。随着扩散的进行,不会发生反扩散,在扩散中改进模型滤波后并没有扩大或缩小高值区的边界范围,即没有模糊边界。

(a) 原始曲线;(b) AD滤波;(c) 线性滤波;(d) 改进模型滤波
图4 3种滤波方法的性能比较
Fig.4 Capability comparison of three filter methods
改进扩散模型(11)满足极值原理[17]:若设 ,
, ,分别表示初始信号灰度的极大值与极小值;2≤C=
,分别表示初始信号灰度的极大值与极小值;2≤C= ,则
,则

 ≤
≤
 ≤
≤
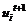 ≥
≥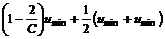 ≥
≥
即
umin≤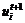 ≤umax
≤umax
4 模拟测试
为测试改进扩散模型对混合噪声的压制效果,分别采用中值滤波、AD滤波法及改进扩散模型滤波对混合噪声进行处理。中值滤波采用3×3的窗口进行计算。利用差分方式按式(11)并采用8邻域逐点计算,阈值k=0.2,扩散迭代次数采用扩散平衡值[18],测试图像所有像素值归一化到0~1之间。测试图像所加的噪声类型为飞点噪声与随机噪声的混合体,测试中飞点噪声的强度σ保持为0.01,而随机噪声强度逐渐增加,从0.01增加到0.10。选择Panda,Camera,Lenna和Boat 4幅图像进行测试,测试结果如表1所示。
表1 不同滤波方法对4种含噪图像处理结果的比较
Table 1 Comparison of image test by different filtering methods

信噪比RSN定义为:

图5所示是窗口为256×256 Camera图像的对比测试结果,其边缘检测对比测试结果见图6。由表1可见:AD滤波后得到的RSN为24.720 dB(图5(c)),而采用本文方法提高到24.918 dB(图5(d));图像的可视化对比效果更明显。由图5(c)可见:存在呈黑白粒状干扰,飞点噪声依然存在,而图5(d)中则没有。在相应的边缘检测图上,采用AD滤波有许多由噪声引起的虚假边缘(图6(c)),图像的上部尤为明显;图6(d)所示的虚假边缘则较少或没有。

(a) 原始图像;(b) 含噪图像;(c) AD滤波; (d) 改进模型滤波
图5 Camera含噪图像去噪处理对比结果
Fig.5 Comparison of Camera image processing
由表1 可以看到:改进模型要优于AD模型和中值滤波。当混合噪声接近于飞点噪声时(随机噪声的强度为0.01),改进模型效果更明显,RSN提高了近2 dB,这主要是因为对“飞点”噪声,具有带通滤波特性的改进模型在扩散过程中受邻域的影响比AD模型滤波大,能有效地处理飞点。AD滤波的主要特点是具有边缘保护特性,能有效地保护图像灰度的高值区[14-15],而“飞点”在AD模型中可能被识别为边缘而予以保护[13],见图6(c)和6(d)。因此,对于结构复杂或纹理丰富的图像如Lenna和Boat图,当噪声接近于飞点噪声时,AD模型滤波效果与中值滤波效果接近,可视效果较差,有明显的虚假边缘存在;当噪声接近于随机噪声时,AD模型滤波效果则与改进模型的滤波效果接近。若图像仅由黑白2种像素组成,则噪声干扰成为飞点,中值滤波效果要优于AD模型但次于改进模型的滤波效果。

(a) 原始图像;(b) 含噪图像;(c) AD滤波;(d) 改进模型滤波
图6 图5中的边缘检测对比测试
Fig.6 Comparison of edge detection
5 结论
(1) 通过调整滤波参数可以改变各向异性扩散的滤波特性,即线性与非线性性、各向同性与各向异性。
(2) 传统的各向异性扩散模型在一定条件下与Robust估计具有等价性,但对“飞点”噪声会引起扩散过程不稳定,发生反扩散。因此,随着扩散不断进行,可能会放大噪声干扰。中值滤波与线性滤波则会导致信号或图像的角点、线条信息损失及边界模糊化。改进扩散模型通过修改扩散项的计算方式使其具有带通特性,当扩散点为“飞点”时,具有中值滤波的特性,能够对“飞点”干扰进行有效压制;当扩散点位于图像或信号的边界上时,它又具有传统各向异性扩散的特性,对边界提供足够的保护。同时,扩散过程稳定并满足极值原理。
(3) 改进模型能够对图像的角点、细线及边缘特征提供足够保护,不会造成特性信息的模糊化。当噪声接近于“飞点”噪声时,改进模型的滤波特性明显优于中值滤波和传统的扩散模型的滤波特性;当噪声接近于随机噪声时,其滤波特性与传统的各向异性扩散类似但要优于中值滤波。因此,改进扩散模型适合于平滑不同强度与形状的混合噪声。
参考文献:
[1] Astola J, Kuosmanen P. Fundamentals of nonlinear digital filtering[M]. Boca Raton: Chemical Rubber Company, 1997: 21-172.
[2] 阮秋琦. 数字图像处理[M]. 北京: 电子工业出版社, 2003: 11-30.
RUAN Qiu-qi. Digital image processing[M]. Beijing: Electronic Industry Press, 2003: 11-30.
[3] Arce G R, Foster R E. Detail preserving ranked-order based filters for image processing[J]. IEEE Trans Acoust, Speech, Signal Processing, 1989, 37(1): 83-98.
[4] Hardie R C, Barner K E. Rank conditioned rank selection filters for signal restoration[J]. IEEE Trans Image Processing, 1994, 3(1): 192-206.
[5] Wendt P D, Coyle E J, Gallagher N C. Stack filters[J]. IEEE Trans Acoust, Speech, Signal Processing, 1986, 34(3): 898-919.
[6] Yang R, Yin L, Gabbouj M, et al. Optimal weighted median filters under structural constraints[J]. IEEE Trans Signal Processing, 1995, 43(3): 591-604.
[7] Ben H A, Luque P, Martinez J, et al. Removing noise and preserving details with relaxed median filters[J]. J Math Imag Vision, 1999, 11(2): 161-177.
[8] Achim A, Ercan E K. Image denoising using bivariate a-stable distributions in the complex wavelet domain[J]. IEEE Signal Processing Leters, 2005, 12(1): 17-20.
[9] Shao M, Nikias C L. Signal processing with fractional lower order moments: Stable processes and their applications[J]. Proc IEEE, 1993, 81(2): 986-1010.
[10] Ben H A, Hamid K. Image denoising: A nonlinear robust statistical approach[J]. IEEE Trans SP, 2001, 49(12): 3045-3054.
[11] LING Jian, Alan C B. Smoothing low-snr molecular images via anisotropic median-diffusion[J]. IEEE Trans Medical imaging, 2002, 21(4): 377-384.
[12] Rousseeu W A, Leroy M. Robust regression and outlier detection[M]. New York: Wiley, 1987: 20-40.
[13] Michael J B, Guillermo Sapiro, David H Marimont, et al. Robust anisotropic diffusion[J]. IEEE Trans IP, 1998, 7(3): 421-432.
[14] Perona P, Malik J. Scale-space and edge detection using anisotropic diffusion[J]. IEEE Trans PAMI, 1990, 12(7): 629-639.
[15] Catte F, Lions P L, Morel J M, et al. Image selective smoothing and edge detection by nonlinear diffusion[J]. SIAM J Numerical Analysis, 1992, 29(1): 182-193.
[16] YOU Yu-li, XU Wen-yuan, Tannenbaum A. Behavioral analysis of anisotropic diffusion in image processing[J]. IEEE Trans IP, 1996, 5(11): 1539-1553.
[17] 余德浩. 微分方程数值解法[M]. 北京: 科学出版社, 2003: 115-200.
YU De-hao. Numerical solutions for partial differential equations[M]. Beijing: Science Press, 2003: 115-200.
[18] 严家斌, 刘贵忠, 甘怡绚, 等. 考虑尺度相关性及几何约束的小波扩散平滑滤波[J]. 中南大学学报: 自然科学版, 2008, 39(6): 1325-1330.
YAN Jia-bin, LIU Gui-zhong, GAN Yi-xuan, et al. Wavelet diffusion filter considering scale correlation and geometry constraint[J]. Journal of Central South University: Science and Technology, 2008, 39(6): 1325-1330.
收稿日期:2009-07-10;修回日期:2009-09-12
基金项目:国家自然科学基金资助项目(40874055);湖南省自然科学基金资助项目(07JJ5065)
通信作者:严家斌(1969-),男,湖南常德人,副教授,从事电磁法数据处理及图像处理研究工作;电话:0731-88877075;E-mail: cspyry@mail.csu.edu.cn
(编辑 陈灿华)