J. Cent. South Univ. Technol. (2010) 17: 857-862
DOI: 10.1007/s11771-010-0567-4
Finite element model updating for large span spatial steel structure considering uncertainties
TENG Jun(滕军)1, ZHU Yan-huang(朱焰煌)1, ZHOU Feng(周峰)2, LI Hui(李惠)2, OU Jin-ping(欧进萍)2
1. Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055, China;
2. School of Civil Engineering, Harbin Institute of Technology, Harbin 150001, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2010
Abstract: In order to establish the baseline finite element model for structural health monitoring, a new method of model updating was proposed after analyzing the uncertainties of measured data and the error of finite element model. In the new method, the finite element model was replaced by the multi-output support vector regression machine (MSVR). The interval variables of the measured frequency were sampled by Latin hypercube sampling method. The samples of frequency were regarded as the inputs of the trained MSVR. The outputs of MSVR were the target values of design parameters. The steel structure of National Aquatic Center for Beijing Olympic Games was introduced as a case for finite element model updating. The results show that the proposed method can avoid solving the problem of complicated calculation. Both the estimated values and associated uncertainties of the structure parameters can be obtained by the method. The static and dynamic characteristics of the updated finite element model are in good agreement with the measured data.
Key words: model updating; uncertainty; interval analysis; multi-output support vector regression; large span spatial steel structure
1 Introduction
Finite element model (FEM) updating is an important part of structural health monitoring. Many experts have developed kinds of model updating methods [1-5]. The common way of model updating is as follows: the measured data are taken as exact references, and the design parameters in FEM are updated in order to minimize the errors of structural responses between the measured and the calculated data. In reality, the assumption of 100% accurate measured data is not completely true [6]. The measured values such as frequencies vary in an interval due to measurement noise and signal processing errors. The measurement uncertainties should be taken into account in model updating [7]. There are several methods to describe the uncertainties of information, such as stochastic method, fuzzy method, and interval analysis. It is better to use the interval analysis method when the number of measured data is small and the character of statistic is difficult to be determined [8-9].
In order to improve the efficiency of model updating, in recent years, model updating methods based on meta-model have been applied widely. Meta-models are mathematical models constructed according to sampling data. They are utilized as the surrogate models for finite element models to describe the function relationship between physical parameters and structural features, such as modal frequencies [10]. Neural networks model and response surface model are two major kinds of meta-models. However, there are some deficiencies of neural network, such as difficulty to determine the structure of the neural network, over-fitting, requiring large numbers of samples, and confining to local maximum. There are also deficiencies of response surface model. For example, it is difficult to fit highly nonlinear model of complex relationship. Support vector machine (SVM) is a new machine learning method based on statistical learning theory. The advantages of SVM are as follows: it is of fast convergence speed, good prediction ability under small amount of samples, and can be fitted by nonlinear model of complex relationship with high precision. Multi- output support vector regression (MSVR) is a new algorithm of SVM, whose output is a vector. The solution will take into account all outputs to construct individual regressor and will be able to obtain the best global prediction [11-12].
In this work, the steel structure of National Aquatic Center (SS-NAC) for Beijing Olympic Games was taken as a case, the uncertainties of measured modal frequencies and errors of FEM were analyzed, and FEM was modified based on interval analysis and MSVR.
2 Theory of interval analysis and MSVR
2.1 Interval analysis
Assume that variable X varies in an interval with upper and lower limits denoted as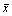 
and x, respectively, then, X=[x, 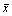]={x|x≤x≤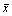} is named as an interval variable. The variation coefficient of the interval variable is defined as δ=ΔX/X c, where ΔX is the interval radius, ΔX=(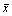-x)/2; and X c is the interval medium value, X c= (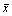+x)/2 [13].
Monte-Carlo method is a numerical simulation to solve the practical engineering problems with the random variables [14]. In fact, it is a statistical method. Firstly, the interval variable is sampled; then, the deterministic analysis is made for the samples; and finally, statistical analysis is made for the output variables. The calculation is enormous when utilizing the Monte-Carlo numerical simulation method. The true value of the interval variable is possible at any point in the interval range. Therefore, the Monte-Carlo method is not utilized for the large and complex structure with uncertainty problem. Latin hypercube sampling is an effective uniform sampling method [15], as compared with Monte-Carlo method, which avoids the duplicate sampling and great number of sampling. In order to reduce the computation, Latin hypercube sampling method was adopted in this work.
2.2 Theory of MSVR
Assuming that x is the input variable, the regression function F(x) can be expressed as
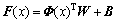(1)
where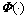
is the nonlinear mapping vector in the high-dimensional space; and W=[w1, w2, …, wN] and B=[b1, b2, …, bN] are defined as N-dimensional linear regressors in the high-dimensional feature space.
According to the theory of SVR, in multi-output cases, structural risk minimization is equal to the following constrained optimization problem:
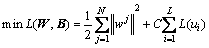(2)
where L(u) is the loss function defined in the hyper-spherical zone expression as follows:
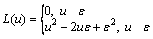(3)
where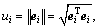 
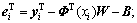and ε is the hyper-spherical insensitive zone. When ε=0, this problem will reduce to an independent regularized kernel least square regression for each component; but for a nonzero ε, the solution will take into account all outputs to construct individual regressor and will be able to obtain the global best predictions [12].
The main steps of FEM updating based on MSVR are as follows.
(1) Construct the samples. Design parameters of the samples are determined based on the uniform design method, and the response values of structure are obtained by analyzing the FEM with design parameters of each sample.
(2) Train the MSVR. The MSVR is trained with the response values and the corresponding design parameters and regarded as the inputs and outputs, individually. The former values are obtained from step (1).
(3) Update the design parameters. The measured response data are input to the trained MSVR. The outputs are the target values of the design parameters.
3 Initial FEM of SS-NAC
National Aquatic Center (NAC) is one of the main venues for Beijing 2008 Olympic Games. The dimensions of NAC are 176.538 m×176.538 m×29.378 m (length× width×height). Polyhedron space frame structures were adopted in the NAC for the first time in the world. In order to reduce the bending stress, small plates were affixed at the ends to strengthen the members. All the walls were supported by the steel-concrete composite beam platform. In the steel structure, rectangular hollow sections were used as chords, circular hollow sections as web members, and welded hollow balls as joints [16].
The FEM of SS-NAC was constructed by the ANSYS program. Beam 189 elements were used to simulate the chord members, the web members were modeled with Pipe 20 elements. Beam 189 was based on Timoshenko beam theory, and shear deformation effects were included. Pipe 20 was a uniaxial element with tension-compression, bending, and torsion capabilities. The members that have little effect on the stiffness were simplified by mass 21 elements on the ball joints. These members included the equipment, pipelines, ethylene- tetrafluoroethylene (ETFE) membranes, and the connected components. All the supports were the fixed-hinged supports. Pre-arch camber was adopted in the construction, and the maximum height of pre-arch was 125 mm. The effect of pre-arch camber was taken into account in the initial FEM of SS-NAC. The view of SS-NAC in the field and the initial finite element model of SS-NAC are shown in Figs.1 and 2, respectively.
Fig.1 View of SS-NAC in field
Fig.2 Initial finite element model of SS-NAC
4 Uncertainty of measured modal frequency of SS-NAC
In order to get the dynamic characteristics of SS-NAC, 18 force balance accelerometers were installed on the welded hollow joints of the roof’s low chord. The location of acceleration measuring points of SS-NAC is shown in Fig.3.
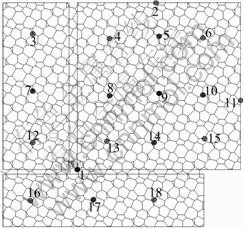
Fig.3 Location of acceleration measuring points of SS-NAC
In order to reduce the effect of temperature and wind on the dynamic frequencies, the acceleration data were selected at different nights in the similar environment (the temperature is 20 ℃ and the average wind speed is smaller than 2 m/s). The typical vibration signal denoised by 4 Hz low-pass filter is shown in Fig.4.
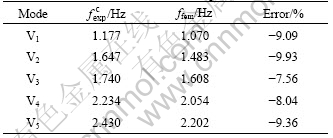
The modal frequencies identified with the wavelet transform are listed in Table 1 [17]. Five vertical modes of SS-NAC were identified with simply named V1, V2, V3, V4 and V5, respectively.
According to Table 1, it can be seen that the measured modal frequencies vary in an interval due to the measurement noise and signal processing errors.
Fig.4 Measured vertical acceleration response of SS-NAC
Table 1 Measured modal frequencies of SS-NAC
Table 2 shows the errors between frequencies calculated from the initial FEM of SS-NAC (ffem) and the corresponding medium value frequencies measured (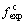
). It can be seen that the errors are relatively large. Therefore, the initial finite model of SS-NAC should be updated.
Table 2 Errors between frequencies calculated from initial FEM of SS-NAC and medium value frequencies measured
5 Error analysis of FEM and selection of updating parameters of SS-NAC
The inaccuracy of FEM results from three factors [18]: (1) model order error, which is mainly due to the finite element mesh size error; (2) model structure error, which is mainly due to simplified assumptions coming from mathematical models, such as assumptions of linear behavior and rigid connections; (3) model parameter error, which is mainly due to material property error and boundary condition error. Both the model structure error and model order error should be small before model updating, otherwise, the initial FEM has to be reconstructed.
5.1 Model order error
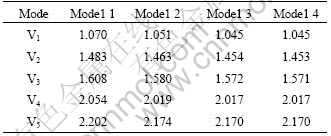
In order to study the effects of mesh size on the structural dynamic response, four kinds of mesh sizes were adopted in the initial FEM. The sizes of mesh grid were 3.00, 1.00, 0.50 and 0.25 m, respectively. The divisions of each chord and web member were automatically calculated (rounded upward to next integer) from the length of each member. The corresponding FEMs were simply named as models 1, 2, 3 and 4, respectively. According to Table 3, it can be seen that there is certain effect of mesh size on computed frequency, but the effect is small. Considering the calculation accuracy and the amount of computation, the mesh size is set to be 1 m.
Table 3 Computed frequencies with different mesh sizes of SS-NAC (Hz)
5.2 Model structure error
There exists an error at the site of joints when using cubic beam elements to simulate the spatial steel structure with welded hollow joints, which is called nodal rigid zone problem. The typical welded hollow joint of SS-NAC in the filed is shown in Fig.5. The body of joint has a certain size and stiffness, which affects the performance of structure. The result of cyclic lateral loading test on a sub-structure model of the SS-NAC also demonstrated that the welded hollow joints had significant contribution to the overall stiffness of the structure [19].
Fig.5 View of welded hollow joint of SS-NAC in filed
Beam elements with rigid zone shown in Fig.6 were adopted in the FEM to simulate the rigid zone. The stiffness of the rigid zone could be adjusted by setting different elastic moduli Er. The length of rigid zone is [19]:
l=r-0.25d (4)
where r is the radius of the welded hollow joint; and d is the diameter of the member.
Fig.6 Modeling of rigid zone of joint
The frequencies of SS-NAC were taken as reference when the elastic modulus of nodal rigid zone Er was set as Er=E=206 GPa. Relative errors of frequencies are illustrated in Fig.7 according to different Er values. It can be seen that the errors do not change obviously when Er is larger than 1 030 GPa, which reveals that the contribution of weld-hollow joints is small and the stiffness of rigid zone is large enough.
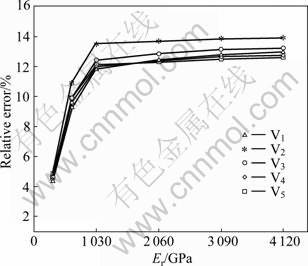
Fig.7 Variation of relative errors of frequencies of SS-NAC with Er
5.3 Selection of updating parameters
In order to analyze the effect of lower concrete supporting system on the dynamic response of SS-NAC, an integral model including the lower concrete supporting system was constructed. The computed error of frequencies between the integral model and the independent steel structure model is very small, probably because the stiffness of the concrete supporting system is very large. Therefore, the supporting system can be simplified as fixed-hinged supports.
According to the characteristics of this project and experiments, the selected parameters for adjustment are outlined as follows: the nodal rigid zone (Er), the elastic modulus of the member (Em), and the mass of non-structural members (mn).
6 Model updating for SS-NAC
6.1 Model updating
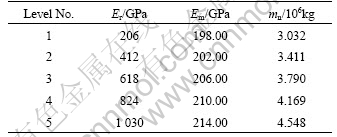
Er, Em, and mn were selected to be updated. The sample for MSVR was constructed by the uniform design method. According to the experience, the values of the three parameters with five levels are listed in Table 4.
Table 4 Parameters of SS-NAC in uniform design
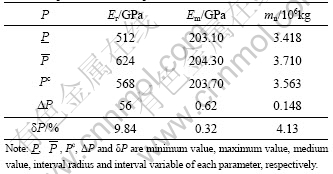
The MSVR was trained with different levels of design parameters and the corresponding frequencies computed from the FEM according to the uniform design method. The interval variables of the measured frequency were sampled by the Latin hypercube sampling method. The samples of frequency were taken as the inputs of the trained MSVR, and the outputs of the MSVR were the target values of design parameters. The updated values of design parameters (simply named P) for SS-NAC are listed in Table 5. It can be seen that the uncertainty of Er is serious.
Table 5 Updated values of parameters of SS-NAC
6.2 Model validation
The computed interval (mm) of the maximum deflection under gravity of the updated model is [198, 203], which is close to the measured value of 197 mm. The comparison of frequencies computed from the updated FEM and measured from filed is shown in Table 6. According to Table 6, it can be seen that they are very close.
Table 6 Comparison of frequencies measured and updated with finite element model of SS-NAC
7 Conclusions
(1) The measured modal parameters vary within an interval due to measurement noise and signal processing errors.
(2) The size of mesh, the elastic modulus of rigid zone of welded hollow joint, the elastic modulus of member and the mass of non-structural members are the major factors that affect the frequency of SS-NAC. Especially, the rigid zone of welded hollow joint should be taken into account in the model updating process.
(3) The model updating method is based on the interval analysis and MSVR avoids dealing with the complicated optimization calculation. Both the estimated values and associated uncertainties of the structure parameters can be obtained. The effect of uncertainty on modal parameters is taken into account in the process of model updating effectively.
(4) The calculated values of static and dynamic response are in good agreement with measured data. The result verifies the feasibility and efficiency of the proposed method.
References
[1] KIM G H, PARK Y S. An improved updating parameter selection method and finite element model update using multi-objective optimization technique [J]. Mechanical Systems and Signal Processing, 2004, 18(1): 59-78.
[2] ZAPICO J L, GONZALEZ-BUELGA A, GONZALEZ M P, ALONSO R. Finite element model updating of a small steel frame using neural networks [J]. Smart Materials and Structures, 2008, 17(4): 1-11.
[3] DING You-liang, LI Ai-qun. Finite element model updating for the Runyang cable-stayed bridge tower using ambient vibration test results [J]. Advances in Structural Engineering, 2008, 11(3): 323- 335.
[4] HE Xu-hui, YU Zhi-wu, CHEN Zheng-qing. Finite element model updating of existing steel bridge based on structural health monitoring [J]. Journal of Central South University of Technology, 2008, 15(3): 399-403.
[5] JAISHI B J Y, REN W X. Structural finite element model updating using ambient vibration test results [J]. Journal of Structural Engineering, 2005, 131(4): 617-628.
[6] STEENACKERS G, GUILLAUME P. Finite element model updating taking into account the uncertainty on the modal parameters estimates [J]. Journal of Sound and Vibration, 2006, 296(4/5): 919- 934.
[7] LI Shun-long, LI Hui, OU Jin-ping. Model updating for Binzhou Yellow River Highway Bridge considering uncertainties [C]// Health Monitoring of Structural and Biological Systems. San Diego: SPIE, 2007: 18-22.
[8] WANG Deng-gang, QIN Xian-rong. Interval method for computational model updating of dynamic structures [J]. Journal of Vibration Engineering, 2004, 17(2): 205-209. (in Chinese)
[9] CAO Wen-gui, ZHANG Yong-jie, ZHAO Ming-hua. Non- probabilistic fuzzy reliability analysis of pile foundation stability by interval theory [J]. Journal of Central South University of Technology, 2007, 14(6): 864-869.
[10] FEI Qing-guo, LI Ai-qun, MIAO Chang-qing. Dynamic finite element model updating using meta-model and genetic algorithm [J]. Journal of Southeast University, 2006, 22(2): 213-217.
[11] PEREZ-CRUZ F, CAMPS-VALLS G, SORIA-OLIVAS E, PEREZ- RUIXO J J, FIGUEIRAS-VIDAL A R, ARTES-RODRIGUEZ A. Multi-dimensional function approximation and regression estimation [C]// International Conference on Artificial Neural Networks. Berlin: Springer, 2002: 757-762.
[12] SANCHEZ-FERNANDEZ M, DE-PRADO-CUMPLIDO M, ARENAS-GARCIA J, PEREZ-CRUZ F. SVM multiregression for nonlinear channel estimation in multiple-input multiple-output systems [J]. IEEE Transactions on Signal Processing, 2004, 52(8): 2298-2307.
[13] SU Jing-bo, SHAO Guo-jian, CHU Wei-jiang. Sensitivity analysis of soil parameters based on interval [J]. Applied Mathematics and Mechanics, 2008, 29(12): 1651-1662.
[14] SHINOZUKA K, ASTILL J. Random eigenvalue problems in structural analysis [J]. AIAA Journal, 1972, 10(4): 456-462.
[15] IMAN R L, CONOVER W J. Small sample sensitivity analysis techniques for computer models, with an application to risk assessment [J]. Communications in Statistics: Theory and Methods, 1980, A9(17): 1749-1842.
[16] FU Xue-yi, GU Lei, YANG Xian-qiao, YU Wei-jiang. Structural design optimization of national swimming center “water cube” [J]. Journal of Building Structures, 2005, 26(6): 13-19. (in Chinese)
[17] YAN B F, MIYAMOTO A. A comparative study of modal parameter identification based on wavelet and Hibert-Huang transforms [J]. Computer-Aided Civil and Infrastructure Engineering, 2006, 21(1): 923-928.
[18] MOTTERSHEAD J E, FRISWELL M. Model updating in structural dynamics: A survey [J]. Journal of Sound and Vibration, 1993, 167(2): 347-375.
[19] HU Xiao-bin, QIAN Jia-ru, FU Xue-yi, GU Lei. Seismic-resisting capacity analysis of a sub-structure model of the National Swimming Center [J]. Spatial Structures, 2007, 13(2): 3-10. (in Chinese)
Foundation item: Project(50678052) supported by the National Natural Science Foundation of China
Received date: 2009-09-18; Accepted date: 2010-01-22
Corresponding author: TENG Jun, PhD, Professor; Tel: +86-755-26033806; E-mail: tengj@hit.edu.cn
(Edited by CHEN Wei-ping)
