J. Cent. South Univ. Technol. (2011) 18: 1080-1086

DOI: 10.1007/s11771-011-0807-2

Multiple phase detector of M-ary phase shift keying symbols in code division multiple access systems

QUAN Zhi

Federal University of Juiz de fora, Electrical Engineering, Juiz de fora, MG Brazil Zip

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: A novel iterative technique, the phase descent search (PDS) algorithm, for M-ary phase shift keying (M-PSK) symbols detection was proposed. This technique constrained the solution to have a unit magnitude and it was based on coordinate descent iterations where coor­dinates were the unknown symbol phases. The PDS algorithm, together with a descent local search (also implemented as a version of the PDS algorithm), was used multiple times with different initializations in a proposed multiple phase detector; the solution with the minimum cost was then chosen as the final solution. The simulation results show that for highly loaded multiuser scenarios, the proposed technique has a detection per­formance that is close to the single-user bound. The results also show that the mul­tiple phase detector allows detection in highly overloaded scenarios and it exhibits near-far resistance. In particular, the detector has a performance that is significantly better, and complexity that is significantly lower, than that of the detector based on semi-definite relaxation.

Key words: coordinate descent; complexity; M-ary phase shift keying (M-PSK); multiuser detection; quadratic optimization; semi- definite relaxation

1 Introduction

In code division multiple access (CDMA) systems, multiuser detection was capable of providing high detection performance [1-2]. However, the complexity of multiuser detectors that were capable of approaching the optimal performance was still a very important issue. For a small-size problem, sphere decoding achieved a nearly optimal performance [3], but became complicated when the size of the problem increased [4]. Semi-definite relaxation (SDR) had also been proposed and investigated for joint detec­tion of a number of symbols with M-ary phase shift keying (M-PSK) modulation [5]. Although promising for multiuser detection, SDR was still complicated for practi­cal implementation [6]. An efficient implementation of multiuser detection, especially in hardware, can be based on the dichotomous coordinate descent (DCD) al­gorithm [7-9]. However, the box-constrained detector did not show good detection performance in highly loaded scenarios. In Ref.[10], a novel technique was proposed for solving a constrained optimization problem corresponding to the optimal detection of M-PSK signals in multiple-input and multiple-output (MIMO) systems. This technique had the detection performance similar to that of the sphere decoder and significantly lower complexity. Later, it was found that this new technique was especially efficient for scenarios where the number of unknown symbols was large. This was typical for CDMA communications. In this work, joint detection of M-PSK symbols was considered in application to multiuser CDMA scenarios and proposed to use the technique from Ref.[10] for this purpose.

2 Problem formulation

The matched-filter output of a symbol synchronous CDMA receiver was given by the K-length vector:

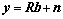                                              (1)

where the vector 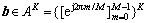 contained M-PSK symbols (from a constellation set A) transmitted by the K users, R was a K×K positive definite sig­nature waveform correlation matrix, and n was a complex- valued zero-mean Gaussian random vector with covariance matrix σ²R, σ²>0 [6].

The maximum likelihood (ML) multiuser detector estimated the vector b by mini­mizing the quadratic function [1]:

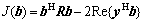                                (2)

with the constraint 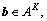 where Re{?} denoted the real part of a complex number. The ML data estimates were given by

                                           (3)

Although the ML detector provided the best detection performance, it was not practical due to its high complexity [1]. Relaxation of the constraint was a general approach that resulted in lower complexity multiuser detectors [6]. As M-PSK symbols had a unit magnitude, the following relaxation was proposed to the original problem Eq.(3):

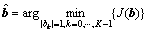                          (4)

where b_k were elements of the vector b. After obtaining an approximate solution to this problem, the final data estimates were obtained by mapping elements of the solution vector into the constellation set A. The problem Eq.(4) was non-convex. Using a convex optimization technique, like the coordinate descent method considered below, can re­sult in a local minimum. Multiple solutions of the problem for a set of initializations would allow finding a ‘smallest’ local minimum. Nevertheless, a small number of such initializations would result in a very high performance of the detector.

3 Proposed detector

The multiuser detector was based on multiple use of the phase descent search (PDS) algorithm [10] as described below.

3.1 Phase descent search (PDS) algorithm

The proposed detector was based on coordinate descent iterations with respect to the unknown symbol phases and a constraint that forces the symbols to have a unit magni­tude. Specifically, the elements of the solution were given by

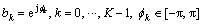                     (5)

The coordinate descent iterations were applied to the phases f_k. The derivation below was based on a general coordinate descent method described in Ref.[11] (see also Ref.[7]). Here, this method was applied to the cost function Eq.(2) with elements b_k from Eq.(5) to derive the PDS algorithm.

Let b(i-1) be a solution obtained at the (i-1)-th iteration; elements of b(i-1) were denoted as b_k(i-1), k=0, …, K-1. At the i-th iteration, the solution b(i) may differ from b(i-1) in the p-th element only. This element may be updated as

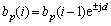                                     (6)

where 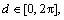 was a step-size parameter (such an iteration was called successful), or it may stay unchanged (such an iteration was called unsuccessful). Depending on a sequence of unsuccessful iterations, the step-size parameter can be reduced. The updated Eq.(6) was expressed as

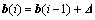
where  e_p was a vector whose elements were zeros except the p-th element which was equal to 1, and

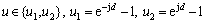
The update was applied (i.e., the iteration was successful) if the cost function Eq.(2) was reduced, i.e.,

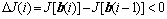
The decrement ?J(i) of the cost function can be written as

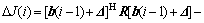
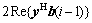                                          (7)

The first two terms in Eq.(7) can be represented as

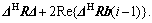
It was easy to see that 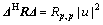 and

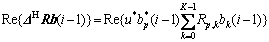
where R_p,k were elements of the matrix R.

As the last two terms in Eq.(7) can be represented as 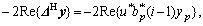 the following equation was finally obtained:

            (8)

where  was the p-th

element of the residual vector r(i-1)=y-Rb(i-1) and y_p was the p-th element of y. It was easy to show that the residual vector can be recursively updated as

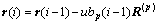                              (9)

with an initialization  where b₀ was an initialization for the solution vector, and R^(p) was the p-th column of R. From Eq.(8), it can be concluded that the i-th iteration was successful if

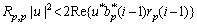                (10)

Now the iterative PDS algorithm can be summarized in Table 1, where p was chosen in a circle order, i.e., p=i_modK, p=0, …, K-1, and it was taken into account that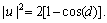

If one of the inequalities at steps 8 or 14 was satisfied, the iteration was success­ful and the element b_p and the residual vector r were updated (steps 10-11 and 16-17, respectively); otherwise, they were not changed. The index n denoted successful it­erations; it was used for introducing the stopping criterion at step 19, where N_u was a predefined parameter that limited the maximum number of updates. If for a pass, including K iterations with p=0, …, K-1, there was no update, the step-size was reduced at step 2: d=d₀λ^m, 0<λ<1, where d₀ was an initial value of d. It was natural to choose d₀=2π. The choice of λ may depend on the modulation scheme used; this would be addressed below. The parameter M_b indicated the number of re­ductions of the step-size d and, thus, the final phase resolution 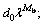 e.g. in the case of λ=1/2 and M_b=6, the final phase resolution was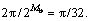

Table 1 Phase descent search algorithm

3.2 Multiple phase detector

The PDS algorithm with a consequent mapping of the solution to the constellation A would be shown to provide a good detection performance for BPSK systems. How­ever, for M-PSK systems with M>2, it did not guarantee high performance. This was because, for a particular initialization, the PDS algorithm can find a local min­imum of the cost function instead of the global minimum. The performance can be improved by multiple use of the PDS algorithm with different starting solutions and a further local search [6] (also implemented using the PDS algorithm) in the multiple phase detector, as shown in Table 2. The multiple use of search algorithms with differ­ent starting solutions was known to be a simple approach for improving the detection performance [6]. Moreover, this approach introduces parallelism in the processing thus making a hardware implementation of the detector efficient.

Table 2 Multiple phase detector

The PDS algorithm was used multiple times with different initializations of the solution vector. To obtain a solution for the q-th initialization b_q, the PDS algorithm was applied twice. The first PDS (step 1 in Table 2) with the consequent mapping (step 2) to the constellation A provided an initial solution, whereas the second PDS (step 3) performed a descent local search moving from one ML feasible solution to another in the neighborhood of the initial solution [6]. Among Q solutions, the one that had the smallest cost function J(?) (computed at step 4) was selected. For the first PDS, a high M_b and λ=1/2 was used. For the second PDS, M_b=1 and λ=1/M were used. The second PDS was initialized by the mapped solution of the previous PDS, 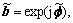 and, according to the values of M_b and λ, it performed M-PSK symbol-flipping (i.e. the descent local search).

4 Implementation issues

The implementation of the proposed multiple phase detector in hardware would be discussed. This detector possessed intrinsic parallelism. It can be imple­mented as Q identical parallel branches, each containing two PDS blocks (correspond­ing to steps 1 and 3 in Table 2), a mapping block (step 2 in Table 2) and a block for computation of the cost function (step 4 in Table 2).

The first PDS blocks in the branches used different initializations of the phase vec­tor φ and, accordingly, different initializations of the solution vector b and the residual vector r. The initial vector b_q in the q-th branch should satisfy the constraint Eq.(5) and therefore it can be represented as 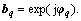 For a fixed vector φ_q, the initial vec­tor b_q can be obtained using a look-up table. The size of the look-up table was as small as  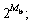e.g. for M_b=6, it contained 64 complex numbers. To initialize the residual vector, one had to calculate the matrix-vector product Rb_q, which, in the general case, would require K² complex-valued multiplications and K(K-1) complex- valued ad­ditions in each branch. This computation was significantly simplified if all elements of the phase vector φ were the same, i.e. Rb_q=c_qR1, where c_q was a complex-valued constant and 1 was a K-length vector of ones. In this case, the vector R1 was calculated once for all Q branches and this calculation did not require multipli­cations. Then, for initialization of the residual vector for each branch, as little as K complex-valued multiplications and K complex-valued additions were required. Mul­tiple simulations with different initializations (not presented here due to lack of space) had shown that the use of  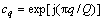provided good detection performance. Since the PDS algorithm provided phases of the solution, the mapping at step 2 became a simple operation. It included truncation (quantization) of M_b-bit elements of the phase vector φ_q into log₂(M)-bit elements of the vector  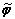and the use of a look-up table of size M to obtain  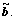These two vectors were used for the initialization of the second PDS blocks in the branches. Note that the proposed choice of the parameters M_b=1 and λ=1/M made the second PDS simple for implementation and, also, it removed the need for symbol mapping after the second PDS.

Now, the implementation of the PDS blocks would be discussed. In the PDS al­gorithm presented in Table 1, there were two stopping criteria: 1) at step 21 upon achieving a predefined phase resolution 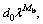 and 2) at step 19 upon performing N_u updates. When implementing in hardware (e.g. on an FPGA platform), other stopping criteria can be used; e.g. the PDS can stop after a predefined number of clock cycles (or execution time). Table 1 showed the complexity of different steps of the PDS algorithm in terms of real multiplications and additions, as well as the maximum complexity. At step 3, the values 1-cos(d) for M_b values of d can be pre-computed. Thus, this step only required K real multiplications. For transforming phases f_p,1 and f_p,2 into complex numbers b_p,1 and b_p,2 (at steps 6 and 12, respectively), a look-up table of size  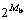can be used, as explained above. The maximum complexity corresponded to a scenario where, for every pass, only one successful iteration happened and the PDS algorithm stopped at step 19, i.e. due to reaching a predefined maximum number of suc­cessful updates N_u. If, in a pass, there were several successful iterations and/or the PDS algorithm stops at step 21, i.e. due to reaching the predefined phase resolution, the complexity would be lower. In the simulation below, N_u high enough was used to guarantee that the PDS algorithm stopped at step 21.

5 Numerical results

Figure 1 showed the bit-error-rate (BER) performance of the proposed detector for BPSK modulated signals against the single-user bound, obtained in 10⁶ simulation trials. The user signature waveforms had equal energies; they were binary and chosen randomly in each simulation trial. The number of users was K=60 and the spreading factor (SF) was 63, i.e. a highly loaded multiuser scenario. The case Q=0 corresponded to the PDS algorithm with a consequent mapping of the solution to the set A (steps 1 and 2 in Table 2). The case M_b=1 with λ=1/2 corresponded to bit-flipping, i.e. changing the p-th coordinate of the solution vector between +1 and -1. The bit-flipping provided a good performance at low SNRs, but, at high SNRs, there was a BER floor. As M_b increased, the BER floor level was reduced; however, the performance at low SNRs became worse. In the case of Q=1, the PDS algorithm was used again at step 3, now with M_b=1, i.e. the second PDS algorithm provided the bit-flipping, which resulted in significant improvement in the BER performance. For the highly loaded scenario, the performance became very close to the single-user bound. The performance had been compared with the single-user bound (instead of the ML performance) because the simulation of ML detector with K=60 users would be impractical.

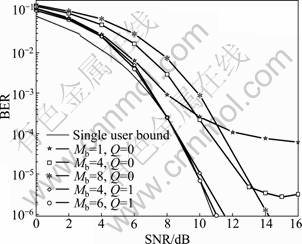
Fig.1 BER performance of multiple phase detector (BPSK modulation, K=60, SF=63)

The BER performance of the proposed detector was employed for a scenario with 4-PSK modulation in Fig.2. The number of users was K=60 and the spreading factor (SF) was 64. For this scenario, complex spreading sequence without energy normalization was used. These results illustrated the gain in BER performance as Q increased and M_b increased. In the case of M_b=6, when Q increased from 1 to 4, the BER performance was significantly improved. While as Q further increased, e.g. Q=20, the BER performance of the proposed detector was reasonably improved, but slightly. For the case Q=4, as M_b increased from 4 to 6, the BER floor level was reduced, whereas the BER curves slightly departed from the single-user bound.

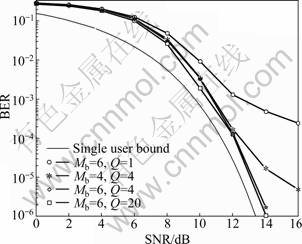
Fig.2 BER performance of multiple phase detector (4-PSK modulation, K=60, SF=64)

Figure 3 showed the BER performance for a scenario with 8-PSK modulation. For this scenario, the use of Q=0 or Q=1 (not shown here) did allow the detection performance to approach the single-user bound. For Q=4, as M_b increased, the BER floor level was reduced, whereas the BER curves slightly departed from the single-user bound. However, for Q=8 and M_b=6 at high SNRs, the BER performance of the proposed detector was very close to the single-user bound. In the simulation, the average number of multiplications was computed in the proposed detector with the best performance in Fig.3, i.e. Q=8 and M_b=6. On average, the detector required approximately 5×10⁵ multiplications to detect all K=10 user symbols. Note that the complexity of the decorrelator (one of the simplest detectors) was approximately K³≈2×10⁵ multiplications, i.e. the complexity of the proposed multiple phase detector with Q=8 branches in such a highly loaded scenario was close to that of the decorrelator. In Ref.[5], complexity results for the SDR detector were presented; specifically, for K=10, the SDR detector required approximately 2×10⁶ multiplications. The simulation results had shown that, in the case of K=10, Q=8 and M_b=6, the proposed detector required on average 1.2×10⁴ multiplications, i.e. two orders of magnitude lower than that of the SDR detector.

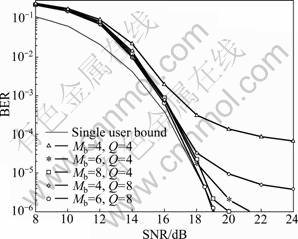
Fig.3 BER performance of multiple phase detector (8-PSK modulation, K=60, SF=63)

Figure 4 compared the symbol-error-rate (SER) performance of the proposed detector against the SDR detector for 8-PSK modulation. The results for the SDR detector were taken from Ref.[5], where the simulation had been done with Gold signature waveforms of length SF=31. The Gold signature waveforms were used in the same scenarios, where the number of users varied from K=20 to K=40. Figure 4 showed that the proposed detector significantly outperformed the SDR detector and the performance of this detector was very close to the single-user bound. The simulation was done by using binary signature waveforms randomly chosen in each simulation trial. It could be seen that the performance was similar or better than that of the SDR detector with Gold signature waveforms.

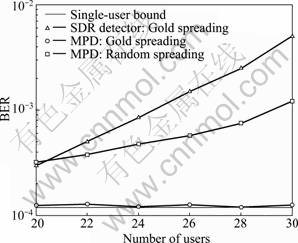
Fig.4 SER performance of multiple phase detector against SDR detector (8-PSK modulation, Q=4, M_b=8, SF=31, SNR=17 dB)

Figure 5 showed the BER performance of the proposed detector in overloaded mul­tiuser scenarios with BPSK modulation where the number of users (K) exceeded the spreading factor SF. The signature waveforms were random binary with equal energies. It was seen that the proposed detector allowed reliable detection even in these dif?cult situations. e.g. for K=60 and as high a load as K/SF≈2, at BER=10^-4, the detection performance departed from the single-user bound by as little as approximately 1 dB. However, this required an increase in the number of branches (initializations) (Q).

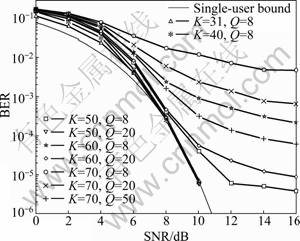
Fig.5 BER performance of multiple phase detector in overloaded scenarios (BPSK modulation, SF=31)

The simulation results had been provided that demonstrated near-far resistance of the proposed detector. The scenarios were considered which all but the first user had the same SNR [6]. In Fig.6, the BER of the first user was shown against the ratio of the strength of the interfering user signals to the first user signal for BPSK modu­lation. In the case of K=10 and SF=32 (this case and the case K=24 and SF=32 were similar to that considered in Ref.[6]), the near-far resistance of the proposed detector was close to that of the ML detector. In this case, increase in Q did not im­prove the BER performance. In the case of K=24, increase in Q resulted in a slight improvement. Note that the direct simulation of the ML detector for K=24 was im­practical, therefore the results cannot be compared with the ML performance. In Ref.[6], the BER performance of an ML detector implemented using a branch and bound al­gorithm based on SDR was given for the same scenario. However, the results showed slightly better near-far resistance compared with the ML performance presented in Ref.[6] (This could be due to approximations made in Ref.[6] or/and a smaller number of simulation trials used in Ref.[6]). It was seen that with further increase of the load (the case of K=60 and SF=63), the proposed detector demonstrated small variations in the near-far resistance. In Fig.7, the BER of the first user with SNR(1) = 16 dB was shown against the ratio of the strength of the interfering user signals to the first user signal. In the case of K=60 and SF=63, the proposed detector with Q=4 had also good near-far resistance for 8-PSK modulation.

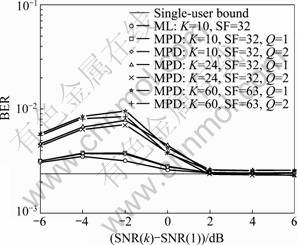
Fig.6 BER performance of multiple phase detector in near-far scenarios (BPSK modulation, SNR(1)=6 dB)

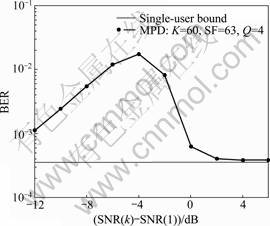
Fig.7 BER performance of multiple phase detector in near-far scenarios (8-PSK modulation, SNR(1)=16 dB)

Finally, the BER performance of the proposed detector was evaluated over a Rayleigh fading channel [12] with BPSK modulation in Fig.8. In this scenario, K=8 and SF=12. Tap L=1 corresponded to flat Rayleigh fading. After that, it was as­sumed that the channel had 3 taps. The channel parameters for this simulation were [0.836 7; 0.447 2; 0.316 2]. The delay was one chip. It was observed that the perfor­mance was improved as L increased above L=1. It was illustrated that the BER per­formance of the proposed detector was significantly improved as Q increased. When Q=4, the performance of the proposed detector had approximately 4 dB gain in comparison with MMSE detector at BER=10^-3.

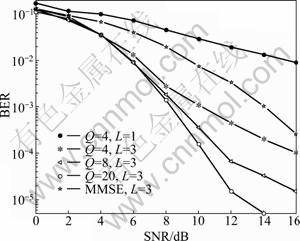
Fig.8 BER performance of multiple phase detector in Rayleigh fading channel (BPSK modulation)

6 Conclusions

1) A novel iterative technique, the phase descent search algorithm, has been proposed for joint detection of multiple M-PSK symbols, i.e. for multiuser detection. The technique provides an approximate solution to the quadratic optimization problem with a con­straint that forces elements of the solution to have unit magnitude. This technique is used multiple times in the proposed multiple phase detector.

2) The simulation results show that for highly loaded scenarios the proposed multiple phase detector has detection performance that is close to the single-user bound. The proposed technique also allows reliable detection in highly overloaded scenarios, e.g. for K=60 and high a load as K/SF≈2, at BER=10^-4 the detection performance departs from the single-user bound by as little as approximately 1 dB and demon­strates good near-far resistance. It has been shown by simulation that the multiple phase detector has a performance that is significantly better, and complexity that is significantly lower, than that of the detector based on semi-definite relaxation.

References

[1] VERDU S. Multiuser detection [M]. Cambridge: Cambridge University Press, U.K, 1998.

[2] FOSCHINI G J, GANS, M J. On limits of wireless communications in a fading environment when using multiple antennas [J]. Wireless Personal Communications, 1998, 6(3): 311-335.

[3] AGRELL E, ERIKSSON T, VARDY A, ZEGER K. Closest point search in lattices [J]. IEEE Trans Inf Theory, 2002, 48(8): 2201-2214.

[4] JALDEN J, OTTERSON B. On the complexity of sphere decoding in digital communications [J]. IEEE Trans Signal Processing, 2005, 53(4): 1474-1484.

[5] MA Wing-Kin, CHING Pak-Chung, DING Zhi. Semi-definite relaxation based multiuser detection for Mary PSK multiuser systems [J]. IEEE Trans Signal Processing, 2004, 52(10): 2862-2872.

[6] TAN Hui-peng, RASMUSSEN, L K. Multiuser detection in CDMA—A com­parison of relaxations, exact, and heuristic search methods [J]. IEEE Trans Wire­less Commun, 2004, 3(5): 1802-1809.

[7] ZAKHAROV Y V, TOZER T C. Multiplication-free iterative algorithm for LS problem [J]. Electronics Letters, 2004, 40(9): 567-569.

[8] ZAKHAROV Y V, TOZER T C. Box-constrained multiuser detection based on multiplication-free coordinate descent optimization [C]// Proceedings of the IEEE Signal Processing Workshop on Signal Processing Advances in Wireless Com­munications. Lisbon, 2004: 11-14.

[9] QUAN Zhi, LIU Jie, ZAKHAROV Y V. FPGA implementation of DCD based CDMA multiuser detector [C]// 15th International Conference on Digital Sig­nal Processing. Cardiff, UK, 2007: 319- 322.

[10] QUAN Zhi, ZAKHAROV Y V, ZHANG Jun-ruo. Multiple phase de­coder for MIMO systems [C]// Proc 42 Asilomar Conf Signals, Systems, and Com­puters. Pacific Grove, CA, USA, 2008: 1759- 1762.

[11] VASILIEV F P. Numerical methods for solution of extremum problems [M]. Nauka, Moscow, 1988. (in Rus­sian)

[12] RASMUSSEN L K, ALEXANSER P D, LIM T J. A linear model for CDMA signals received with multiple antennas over multipath fading channels [C]// CDMA Techniques for Third Generation Mobile Systems. Kluwer: Academic Pub­lishers, 1999: 23-57.

(Edited by YANG Bing)

Received date: 2010-05-12; Accepted date: 2010-10-08

Corresponding author: QUAN Zhi, PhD; E-mail: {zhi.quan}@engenharia.ufjf.br