J. Cent. South Univ. Technol. (2008) 15: 882-887

DOI: 10.1007/s11771-008-0161-1

New two-dimensional fuzzy C-means clustering algorithm for

image segmentation

ZHOU Xian-cheng(周鲜成)^{1, 2}, SHEN Qun-tai(申群太)¹, LIU Li-mei(刘利枚)^{1, 2}

 (1. School of Information Science and Engineering, Central South University, Changsha 410083, China;

2. School of Computer and Electronic Engineering, Hunan University of Commerce, Changsha 410205, China)

Abstract: To solve the problem of poor anti-noise performance of the traditional fuzzy C-means (FCM) algorithm in image segmentation, a novel two-dimensional FCM clustering algorithm for image segmentation was proposed. In this method, the image segmentation was converted into an optimization problem. The fitness function containing neighbor information was set up based on the gray information and the neighbor relations between the pixels described by the improved two-dimensional histogram. By making use of the global searching ability of the predator-prey particle swarm optimization, the optimal cluster center could be obtained by iterative optimization, and the image segmentation could be accomplished. The simulation results show that the segmentation accuracy ratio of the proposed method is above 99%. The proposed algorithm has strong anti-noise capability, high clustering accuracy and good segment effect, indicating that it is an effective algorithm for image segmentation.

Key words: image segmentation; fuzzy C-means clustering; particle swarm optimization; two-dimensional histogram

1 Introduction

Due to the disregard of spatial constraint information, the fuzzy C-means (FCM) algorithm failed to segment images corrupted by noise^[1-2]. In order to improve the robustness of FCM to noise, some methods using the spatial neighbor information of the image were proposed^[3-5]. Currently, the relative successful methods include: The method using the neighborhood bound as the punish function to modify the clustering objective function was put forward by CHEN and ZHANG^[6]; the new distance measuring method instead of the Euclidean distance as the standard of the different measure was used by YU et al^[7]; the weight theory to correct membership function of the pixels was exerted by WANG et al^[8] and AHMED et al^[9]; the image segmentation algorithm using fuzzy C-means clustering (FCM) with spatial constraints based on Markov random field (MRF) via Bayesian theory was proposed by LI et al^[10]. Owing to the advantages of the gray information and the spatial neighbor information of the image, these methods greatly improve the segmentation effect of the noisy image compared with the traditional FCM. But problems still exist: it is easy to get into the local convergence, the convergence is slow and the effect of noise suppression is not so good for cluster center is still gained by iterative optimization of FCM algorithm.

In this work, a novel image segmentation algorithm using the gray information and the spatial neighbor information of the image was proposed. Firstly, an improved two-dimensional gray histogram was constructed. Secondly, the fuzzy cluster centre was obtained by using the predator-prey particle swarm optimization (PPPSO), and the membership function for every pixel to cluster center was calculated, then the fuzzy cluster for every pixel of two-dimensional histogram was accomplished by using the fuzzy C-means clustering algorithm. Finally, according to the membership function, the pixel classification was finished, and image segmentation come true. Because the gray information and the spatial neighbor information of each pixel were taken into consideration, the problem that the object and background in the one-dimensional histogram were not distinguished easily was solved. Due to the global searching ability of the predator-prey particle swarm optimization (PPPSO), the optimal clustering center could be obtained by optimization.

When the fuzzy C-means clustering algorithm is applied in image segmentation the image pixels are treated as a set S (S=s_k, k=1, 2, …, n) of n stylebooks that are divided into C (2≤C≤n) clusters to make image division come true according to the weighted comparability measuring between image and clustering center. Now, it is supposed that the vector m_i (i=1, 2, …, C) is the cluster center, and μ_ik is the membership function for the kth stylebook to the ith class. They satisfy

the condition 0≤μ_ik≤1 and  then the cluster-

ing objective function defined by membership function is as follows:

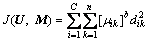                     (1)

where  U=[μ_ik] is the fuzzy classing matrix; M={m₁, m₂, …, m_C} is the set of C cluster centers; b=[1, ∞] is a weighted index, the larger the b, the fuzzier the division, and in this work, b is 2; parameter d_ik means the Euclidean distance from the kth stylebook to the ith cluster center.

The fuzzy clustering image segmentation is to confirm the membership function μ_ik and the cluster center m_i by iterative according to the clustering rule of minimizing the objective function J(U, M). By the Lagrange multiplier, the calculating formulae of μ_ik and m_i can be shown as formulae (2) and (3). If the data set S, the number of the clustering class C and the weighted index b are known, then the membership function and the cluster center can be defined by Eqns.(2) and (3) in the process of iteration^[11].

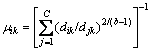                     (2)

                             (3)

3 Particle swarm optimization

3.1 Basic particle swarm optimization

Particle swarm optimization (PSO) is a population- based stochastic optimization algorithm modeled after the simulation of the social behavior of bird flocks, which has the capability of parallel search and effective use of the global information^[12]. In a PSO system, a swarm of individuals (call particles) fly through the search space. Each particle represents a candidate solution to the optimization problem. The position of the ith particle is signed by x_i(x_i1, x_i2,…, x_id), the flight speed is signed by v_i(v_i1,v_i2,…, v_id). The personal best position of particle i is the best position visited by particle i so far, is signed by p_i(p_i1, p_i2,…, p_id). The global best position is the best position visited by all particles so far, is signed by p_g(p_g1, p_g2,…, p_gd). In every iteration of PSO, the particle’s speed and position are updated by dynamic tracking the parameters p_i and p_g:

v_ij(t+1)=ωv_ij(t)+c₁r_1j(t)[p_ij(t)-x_ij(t)]+c₂r_2j(t)[p_gj(t)-x_ij(t)]

(4)

x_ij(t+1)=x_ij(t)+v_ij(t+1)                          (5)

where  i represents the ith particle; j represents the jth dimension of the particle; t represents the tth iteration; ω is the inertial coefficient; c₁ and c₂ are the learning factors, and they are usually valued within 0-2; r₁ and r₂ are independent random numbers valued between 0 and 1. To make the algorithm get better global searching ability in early times and local searching ability in advanced times, ω can be improved; as the iteration proceeds, the inertial coefficient (ω) in speed updating formula can be reduced to the minimum weighted factor (ω_min) from the maximum weighted factor (ω_max)^[13].

3.2 Predator-prey particle swarm optimization

PSO is easy to get into the local optimum. Illumined by the convolution of predator and the prey, the predator-prey particle swarm optimization (PPPSO), proposed by bringing the predator-prey model into the particle swarm optimization, is able to keep the diversity of the swarm and avoid the algorithm becoming early convergence^[14-15]. In this method, particles are divided into two categories, predator and prey. Predators show the behavior of chasing the center of preys’ swarm, which looks like chasing preys. And preys escape from predators in multidimensional solution space. This is contributed to making the particles avoid the local optimal solutions and finding the global optimal solution. In predator-prey PSO, the velocities of tracking predator and prey are expressed as

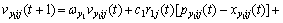
             (6)

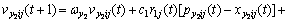
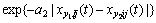                    (7)

where  subscripts y₁ and y₂ mean predator’s and prey’s respectively; p_g is the global best position which predators and preys share; subscript I is the number of a predator which is chosen like

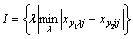                       (8)

That is, at every iteration and at every dimension, the nearest predator for each prey is chosen. The fourth term in Eqn.(7), P is binary variable, 0 or 1 stochastically, that determines if the prey escapes or not; a₁ and a₂ are the parameters which determines how hard preys escape from predators. And the nearer the distance between the prey and predator is, the harder the prey escapes from the predator. Consequently, preys keep escaping from predators and predators keep occupying around p_g best from one iteration to the next.

4 Design of novel two-dimensional FCM clustering algorithm for image segmentation

Some modified algorithms were applied to restraining the infection of noise to cluster effectively via considering spatial and neighborhood information of pixel for the result of the traditional FCM algorithm to noisy image segmentation was worse. Although the spatial neighbor information of image was taken into account in all kinds of improved algorithms, the algorithm was involuntary to get into local optimum and could not obtain the optimum or even satisfactory solution as cluster center was gained by virtue of FCM iterative hill-climbing. In the proposed method, clustering image segmentation was converted into an optimization problem. Predator-prey particle swarm algorithm was a global optimization algorithm, and had a global searching ability to search the optimum cluster center in the entire space for solution, and could avoid to get into early convergence.

4.1 Improved two-dimensional gray histogram

According to the filtering templates, pixels around a pixel can be a neighborhood to calculate the neighborhood gray value. The two-dimensional histogram of the image is constructed by the pixel gray value and its neighborhood gray value. The neighbor- hood gray value can be the neighborhood gray mean value and also can be the neighborhood gray median value. While smoothing image, the mean filter will fuzzy the boundary, so the filtering is not so good. The median filter can protect the border information effectively. Especially for the salt-and-pepper noise and the Gaussian noise, the filtering is very well. To make full use of the spatial neighborhood information, an improved two- dimensional histogram method was adopted in this work. Firstly, do the median filter to the image, and use it as the one-dimensional (1D) information of the two- dimensional (2D) histogram, and then do the second median filter. The gained result can be the other dimension. So, the improved two-dimensional gray histogram is constructed by the median value of the neighborhood first median filter and the median value of the neighborhood second median filter. In this way, it can protect the border information effectively.

4.2 Design of population and confirmation of fitness function

In the optimization, the parameter to be optimized is the cluster center of the image. Therefore, the swarm can be designed to be a group of cluster centers, which is represented by a particle. The size of the dimension of the particle represents the number of the cluster center, viz. particle x_i can be shown by x_i={m_i1, m_i2, …, m_iC}, where m_ij is the jth clustering central vector of the ith particle. For the fitness function, the influence on the clustering coming from the neighborhood information of the pixel should be considered to improve the noise suppressing ability of the algorithm. Thereby, the neighborhood punish function is brought into the fitness function according to the improved two-dimensional gray histogram above. So the fitness function can be designed as

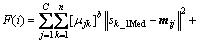
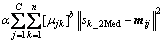             (9)

where  F(i) means the fitness function; s_{k_1Med}  represents the median value of the first neighborhood median filter; s_{k_2Med}  represents the median value of the second neighborhood median filter.

4.3 Design of algorithm

When algorithm gets into the convergence, the particle that has the minimum fitness will be the optimal particle, and the cluster centers will be the optimal ones, then the image segmentation will be accomplished by the clustering segmentation in which the cluster center is confirmed by the optimal particle. The specific steps to achieve it are as follows.

1) Do the second median filter to the given image to be segmented, and get the improved two-dimensional gray histogram.

2) Set the predator and prey population size; then set the dimension of the particle to be C which is the size of the clustering class and initialize the predator and the prey particle, and make every dimension of the particle to be a real number between 0 and 255; set the initialized speed and the related parameters in the algorithm.

3) Initialize the global optimal position of the swarm and the individual optimal position of every particle.

4) Calculate the distance from every pixel and the cluster center by the defined cluster center, and the membership function for every pixel to the cluster center.

5) Calculate the fitness value for every particle. Choose Eqn.(9) as the fitness function of the PSO, and calculate the fitness value of every particle by the result from step 4).

6) Compare the fitness value of every particle with the value of the best position (p_i) it has visited. If it is better, then the value will be the current best position; the same comparison is made in every swarm to get the best global position.

7) Update the predator’s speed 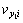 and position  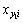by Eqns.(6) and (5).

8) Update the prey particle’s speed 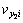 and position  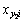by Eqns.(7) and (5).

9) If the stopping condition is satisfied, the algorithm is over. The global optimal solution p_g will be the optimal cluster center to be found ultimately; or else, jumps to step 4).

10) Do the image segmentation by the optimal cluster center gained from the optimization.

5 Comparison of simulation results

5.1 Simulation results

To verify the effectiveness of the algorithm in this work, comparative experiments were done. The ways to be compared included: the standard FCM and FCM_S based on neighborhood median value proposed by PHAM^[3]. The experimental parameters in this work were: the size of the predator particle swarm was 5 , the size of the prey particle swarm was 25, c₁ and c₂ were 1.49, ω_max was 0.9, ω_min  was 0.2, and p_f=0.02. The simulation to the segmentation algorithm was programmed by Matlab software.

The size of the constructed synthetic image was 128×128, containing 2 gray values of 60 and 200. As a result, the number of the class was set to be 2 in the segmentation. To compare the anti-noise performances of the 3 methods above, Gaussian noise with mean of 0 and variance of 0.04 to the synthetic image was added. The experimental results are shown in Fig.1. It can be seen from Fig.1 that the traditional FCM is useless to the noise, and the segmentation is far from ideal because its segmentation is based on the current pixel; FCM_S greatly improves the anti-noise result because of the neighborhood restriction, but there is still some noise; due to the consideration of spatial neighborhood information, the optimal cluster center can be obtained by optimization, the visual effect of the segmentation is very good by the algorithm proposed in this work, which is much better than the other 2 methods .

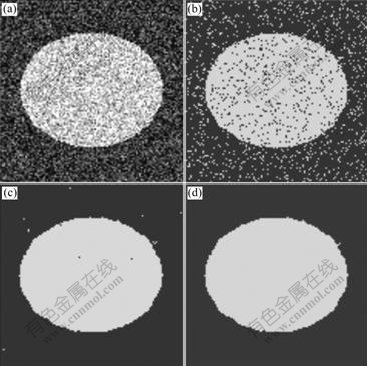
Fig.1 Experimental results of synthetic image with Gaussian noise: (a) Gaussian noise corrupted image; (b) Result by FCM; (c) Result by FCM_S; (d) Result by proposed method

5.2 Performances comparison

The accuracy of the segmentation was assessed with pixel number error (PNE) and the segmentation accuracy ratio (SAR). PNE is the number of the fault-partition pixels, and SAR is the ratio of correct categorization pixels to the total image pixels. The segment image without the noise using FCM or original image was reference object to judge whether the pixel was categorized correctly^[9].

Gaussian noises with mean of 0 and variance of 0.04 and mean of 0 and variance of 0.09 were added separately to the synthetic image, and the obtained cluster centers, misuse pixels and segmentation accuracy ratio with different noises by 2 methods were compared. The comparison of performance of clustering segmentation of several algorithms is listed in Table 1. Values in the Table 1 are the mean value of 10 algorithmic operations. From the cluster center obtained, because the two methods FCM and FCM_S in membership function and cluster center have the same calculating formula, the consistent cluster center can be obtained. At the same time, they are affected by the noise. As the noise becomes stronger, the error of the cluster center becomes larger. But the proposed algorithm has strong anti-noise ability, nice cluster center, and little influence by the noise. From accuracy of classification, FCM has more misuse pixels, and the segmentation accuracy from FCM is lower. As the noise becomes strong, the misuse pixels increase quickly, and the segmentation accuracy lowers down apparently. When the noise is lower, the misuse pixels of FCM_S are little and segmentation accuracy is high, but as the noise becomes strong, the misuse pixels increase, and the segmentation accuracy lowers down. The proposed algorithm has little misuse pixels, high segmentation accuracy; the influence of noise on the segmentation is not so great; the anti-noise ability and the degree of accuracy in the clustering segmentation is better than the other 2 methods.

Table 1 Comparison of performance of clustering segmentation of several algorithms

5.3 Simulation results analysis

The simulation results and performance comparison indicate that the proposed algorithm is better than the FCM and FCM_S algorithms. The reasons are mainly in two aspects. One is that the improved two-dimension histogram is adopted in the proposed algorithm. The synthetic image histogram with mean of 0 and variance of 0.04 are shown in Fig.2. Fig.2(a) and Fig.2(b) are one- dimensional and two-dimensional histogram, respectively. In Fig.2(a), it is difficult to discern the object and background with overlapping in one- dimensional histogram after noise is added in the synthetic image, and this is the major cause that the FCM algorithm fails to segment images corrupted by noise. When the improved two-dimensional gray histogram is adopted, two distinct peaks emerge in this histogram, and it is easy to distinguish the object and background in Fig.2(b). The other reason is that the algorithm utilizes the global searching ability of particle swarm algorithm to search the cluster center in the entire solution space, and the optimal cluster center can be obtained by predator-prey particle swarm algorithm.

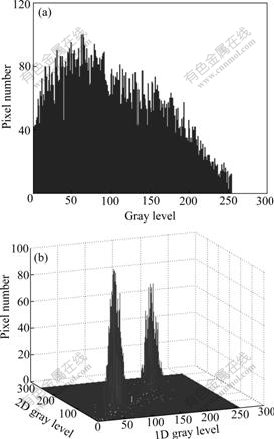
Fig.2 Histogram of synthetic image: (a) One-dimensional histogram of synthetic image; (b) Improved two-dimensional histogram of synthetic image

1) Using the gray information and the neighbor relations between the pixels, an improved two- dimensional histogram is constructed. According to the improved two-dimensional histogram, the objective function of traditional FCM algorithm is modified, and the fitness function including neighbor information of the image is established.

2) Utilizing the global searching ability of the predator-prey particle swarm optimization (PPPSO), the optimal cluster center can be obtained by optimization.

3) In the noisy image segmentation, the proposed algorithm is less in misclassification pixel, higher in segmentation accuracy, stronger in anti-noise ability, and behaves much better than the current two-dimension fuzzy mean algorithm.

References

[1] LIEW A W, YAN H, LAW N F. Image segmentation based on adaptive cluster prototype estimation [J]. IEEE Transactions on Fuzzy Systems, 2005, 13(4): 444-449.

[2] LIU Y T. A genetic clustering algorithm for data with non-spherical shape cluster [J]. Pattern Recognition Letter, 2000, 33(1): 1251- 1259.

[3] PHAM D L. Fuzzy clustering with spatial constraints [C]// Proceedings of the IEEE International Conference on Image Processing. New York: IEEE Computer Society, 2002, 2: 65-68.

[4] DENG Hua, WU Yi-hu, DUAN Ji-an. Adaptive learning with guaranteed stability for discrete-time recurrent neural networks [J]. Journal of Central South University of Technology, 2007, 14(3): 685-690.

[5] WANG Xiu-juan, SHI Hong-bo. Clustering and fuzzy neural network for fuzzy rule sets modeling [J]. Journal of Central South University of Technology, 2003, 34(4): 360-362. (in Chinese)

[6] CHEN Song-can, ZHANG Dao-qing. Robust image segmentation using FCM with spatial constraints based on new kernel-induced distance measure [J]. IEEE Transactions on Systems, Man, and Cybernetics, 2004, 34(4): 1907-1916.

[7] YU Jin-hua, WANG Yuan-yuan, SHI Xin-ling. Image segmentation with two-dimension fuzzy cluster method based on spatial information [J]. Opto-Electronic Engineering, 2007, 34(4): 114-119. (in Chinese)

[8] WANG X, WANG Y, WANG L. Improving fuzzy C-means clustering based on feature-weight learning [J]. Pattern Recognition Letter, 2004, 25(10): 1123-1132.

[9] AHMED M N, YAMANY S M, MOHAMED N. A modified fuzzy C-means algorithm for bias field estimation and segmentation of MRI data [J]. IEEE Trans on Medical Imaging, 2002, 21(3): 193-199.

[10] LIXiao-he, ZHANGTai-yi, QUZhan. Image segmentation using fuzzy clustering with spatial constraints based on Markov random field via Bayesian theory [J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2008, 91(3): 723-729.

[11] GAO Xin-bo. Fuzzy cluster analysis and its applications [M]. Xi’an: Xidian University Press, 2004: 50-54. (in Chinese)

[12] CLERC M, KENNEDY J. The particle swarm: Explosion, stability, and convergence in a multi-dimensional complex space [J]. IEEE Transaction on Evolutionary Computation, 2004, 6(11): 58-73.

[13] van DEN BERGH F. An analysis of particle swarm optimizaters [D]. Pretoria, South Africa: University of Pretoria, 2001.

[14] SILVA A, NEVES A, COSTA E. An empirical comparison of particle swarm and predator prey optimization [C]// Proceeding of the Artificial Intelligence and Cognitive Science: 13th Irish International Conference. Berlin: Springer-Verlag, 2002: 103-110.

[15] HIGASHITANI M, ISHIGAME A, YASUDA K. Particles swarm optimization considering the concept of predator-prey behavior [C]// Proceedings of 2006 IEEE Congress on Evolutionary Computation. New York: IEEE Computer Society, 2006: 434-437.

Foundation item: Project(06JJ50110) supported by the Natural Science Foundation of Hunan Province, China

Received date: 2008-03-26; Accepted date: 2008-06-15

Corresponding author: ZHOU Xian-cheng, Associate professor, Doctoral candidate; Tel: +86-731-8688272; E-mail: zxc6501@126.com

(Edited by YANG Hua)