
Computational simulation of fluid dynamics in a tubular stirred reactor
CAO Xiao-chang(曹晓畅), ZHANG Ting-an(张廷安), ZHAO Qiu-yue(赵秋月)
School of Materials and Metallurgy, Northeastern University, Shenyang 110004, China
Received 21 May 2008; accepted 10 October 2008
Abstract: The flow and concentration fields in a new style tubular stirred reactor were simulated by simulating the fluids dynamics(CFD), in which FLUENT software was used and the standard k—ε model and multiple reference frame(MRF) were adopted. The various values of initial rotating speed and inlet flow rate were adopted. Simulations were validated with experimental residence time distribution(RTD) determination. It is shown that the fluid flow is very turbulent and the flow pattern approaches to the plug flow. The velocity increases from shaft to the end of impeller, and the gradient is enlarged by increasing the rotating speed. Comparison between RTD curves shows that agitation can improve the performance of reactor. As the flow rate increases, the mean residence time decreases proportionally, and the variance of RTD lessens as well. When rotating speed increases to a certain value, the variance of RTD is enlarged by increasing rotating speed, but the mean residence time has no obvious change.
Key words: computational fluid dynamics(CFD); residence time distribution(RTD); tubular stirred reactor
1 Introduction
Reactor is the key piece of equipment in all hydrometallurgical digestion process. In the current study, an innovative tubular stirred reactor was examined, and it is possible that such a reactor would have many applications. The reaction kinetics and the yield are, to a great extent, decided by the type and the size of the reactor, and thus the selection, design, calculation and the optimization conditions are of importance in the chemical and metallurgical production. Based on the principle of raising efficiency, reducing investment and production costs, a new style multi tubular reactor was developed in Northeastern University(NEU), China, using the theory of agitation mixing. The concept design aims to overcome some of the disadvantages of the traditional tubular reactors that are industrially available.
An agitation device is simply added to the traditional tubular reactor and sixteen groups of T-type blades are distributed uniformly in the agitating shaft. These blades have the function of strengthening the mixing effects, and the transverse blades can help continually to scrape the wall and thus decrease or even eliminate scabs.
Computational fluid dynamics(CFD) is an effective approach for the design and optimization of the stirred reactor[1-5], and has been frequently used in the analysis of the reactor characterization in various applications in recent years[6-8]. In this study, a commercial code FLUENT 6.3 (FLUENT Inc.) was used to simulate the new style stirred reactor with inlet mass flow at various rotating speeds, and the residence time distribution(RTD) and flow field were investigated. The objective of the present study is to characterize the flow behavior of tubular stirred reactor. CFD predictions are validated with experimental RTD curves. The CFD analysis can improve the performance of the reactor and reduce testing in experiments.
2 Experimental
The stirred vessel investigated is a tubular reactor with a multi-bladed impeller, as schematically shown Fig.1. The cylindrical vessel is 2 m in length and 0.186 m in diameter; and the inlet and outlet diameters are 0.04 m. The impeller is composed of sixteen groups of T-type blades with 0.09 m in height and 0.12 m in width, each of which is 0.09 m in height and 0.1 m in width. Water at 25 ℃ was used as the test fluid. The reactor was filled by water when mass flow rates at inlet and outlet were monitored and controlled by the mass flow meter.
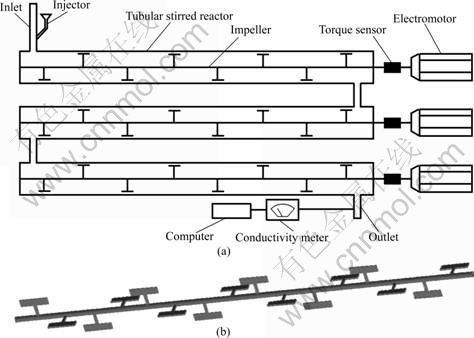
Fig.1 Schematic maps of experimental setup (a) and impeller (b)
The RTDs were determined experimentally by adopting the classical tracer response technique[9]. Different impeller speeds and inlet mass flow rates were investigated in the mixing experiments. An inert chemical tracer was injected into the reactor promptly when the flow tended to steady; meanwhile, measurements of solution conductance were carried out using conductivity meter. The effluent conductance—time curve is referred as concentration(C) curve in RTD analysis, and C(t) is divided by the integral to obtain the E(t) curve from C(t) curve. The dimensionless RTD function E(θ) was also used by defining the dimensionless time in the following form:
E(θ)= ?E(t) (1)
?E(t) (1)
where θ(= ) is the dimensionless time; and
) is the dimensionless time; and  (
( =
=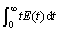 ) is the mean residence time.
) is the mean residence time.
3 Numerical simulation
The numerical simulation was carried out using a commercial CFD package ANSYS FLUENT, which is based on finite-volume methods. 3D geometry is created and meshed using the commercial grid-generation tool GAMBIT software (FLUENT Inc.) with tetrahedral elements, containing 1 329 440 cells totally. Part of grid of tubular stirred reactor is shown in Fig.2. Compared with the numerical prediction, the amount of mesh is adequate for this simulation.

Fig.2 Part of grid of tubular stirred reactor
The prediction of turbulent flow is based on the numerical solution of the time-dependent, three- dimensional, Reynolds-averaged continuity and Navier-Stokes equations. The standard k-ε model has been widely used for modeling turbulent flow in the stirred reactor and it is the most common turbulence model for analyzing engineering flows. The variations of the k-ε model such as Renormalized Group(RNG) k-ε model, which can give superior results for isotropic turbulence, is also applied in flow predictions in stirred reactors, but there are only slight changes in turbulence predictions. RNG k-ε model can give superior results for isotropic turbulence. Large Eddy Simulation(LES) for modeling flow in the stirred reactor shows good agreement with experimental data for both velocities and turbulence quantities. However, due to the associated computational expense and limitations of grid requirements, LES model is impractical for many research requirements[10]. Hence, the standard k-ε model was used in this work. The governing equation for turbulent kinetic energy, k, and turbulent energy dissipation rate, ε, are written as:
 (2)
(2)
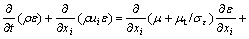
 (3)
(3)
where μt is turbulent viscosity and G is turbulence generation rate.
 (4)
(4)
G=μt[(uy+vx)2+(vz+wy)2+(wz+uz)2+2(ux+vy+wz)2] (5)
The standard k-ε model constants are: c1=1.44, c2= 1.92, cμ=0.09, σk=1.0, σε=1.3.
For simulating the flows generated by the impeller, there are two common approaches: one is Multiple Reference Frame(MRF), and the other is Sliding Mesh (SM) approach. Usually, the MRF method is for steady-state flow while SM is for unsteady flow[11]. In this work, the MRF model has been shown to perform well for this configuration, and thus was selected. The whole vessel is divided into two regions: the impeller zone and the stationary zone. The solution is matched at the interface between the rotating and the stationary region via velocity transformation from one frame to the other. In this way, the equations for the fixed and the rotating part of the mesh were solved separately and the effects of the blade rotation were accounted by virtue of the reference frame.
The convection term in the governing equations was modeled with the bounded second-order scheme and SIMPLE algorithm was used to resolve the coupling between velocity and pressure[12]. The criteria of 10-4 were set for the residuals of continuity, velocities, k, and ε equations to determine the convergence of solution, with this value being considered sufficient to have a converged simulation. All simulations were carried out by a workstation equipped with two Intel Xeon 3.0 Hz processors, 16GB RAM, using parallel technique in FLUENT.
In the experiments, water was used as the test fluid. The simulation of RTD has been carried out by injecting a pulse of a tracer at the inlet. The two-species transport model was applied in RTD prediction. A single-species flow field was first obtained under steady-state model. The tracer with the same properties as the water was introduced at the entrance with a momentary pulse using transient model. In this way, the C/C0 can be obtained directly from the results of the outlet.
4 Results and discussion
4.1 Analysis of fluid field
In Fig.3, the results of the simulation are presented graphically (Q=1.8 m3/h, N=150 r/min). Under the effect of agitation, the distribution of velocity shows that the flow field is very turbulent. In the illustration of segmental system, the fluid flows along the shaft in helical, and axial mixing is generated by the rotating impeller. It can be seen from part of vector plot of velocity that agitation can accelerate the flow near wall surface of reactor, which can prevent the appearance of scaling. Fig.4 shows the comparison of Z-axial velocity in different radial distances at different rotating speeds (Q=1.8 m3/h), and Fig.5 shows the radial velocity at different rotating speeds in the center of the vessel. It is demonstrated that the velocity magnitude increases from shaft to the ends of the impeller. As the impeller speed increases, fluid-resistance appears near wall surface by means of centrifugal force. The velocity magnitude is well distributed at N=50 r/min for low centrifugal force.
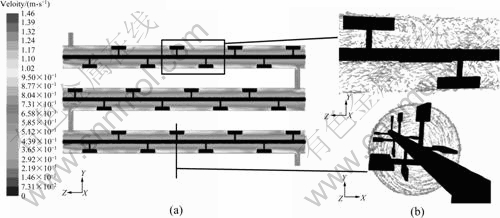
Fig.3 Contour plot of velocity (a) and part of vector plot of velocity (b) (Q=1.8 m3/h, N=150 r/min)
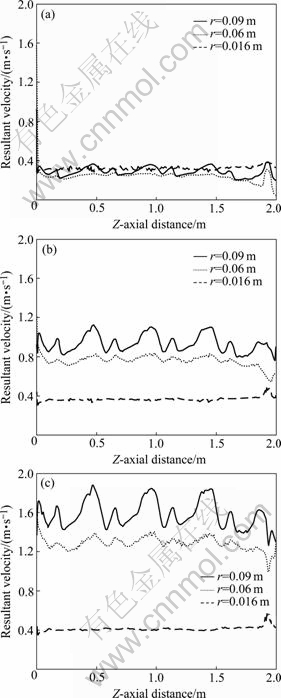
Fig.4 Comparison of Z-axial velocity in different radial distances at flow rate of 1.8 m3/h: (a) 50 r/min; (b) 150 r/min; (c) 250 r/min
Different optimum impeller speeds are obtained at different inlet flow rates. The optimum impeller speed is 50 r/min while inlet flow rate is 1.8 m3/h.
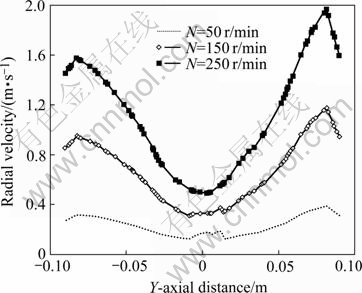
Fig.5 Radial velocity in different impeller speeds at flow rate of 1.8 m3/h
4.2 Characteristics and profiles of RTD functions
The experimental C(t) curves were used to obtain information about the mean fluid residence time, the variance of distributions, σ2, and the RTD distribution functions at the reactor exit, inclusively in normalized form E(θ). The E(θ) curves show the presence of stagnant zones. When the maximum of E(θ) appears at θ<1, it indicates the presence of short-circuits; while the maximum of E(θ) appears at θ>1, it indicates the presence of the back mixing. The width of RTD curve is an appropriate measurement to determine the approach to plug flow[13-15]. Fig.6 shows the comparison of the RTD curves by simulations with experimental data, in which the two are accordant, especially at low rotating speed, indicating that CFD approach used in this work is reliable for simulating the RTD curves of the tubular stirred reactor.
Fig.6 Comparison of RTD curves between simulations and experimental data
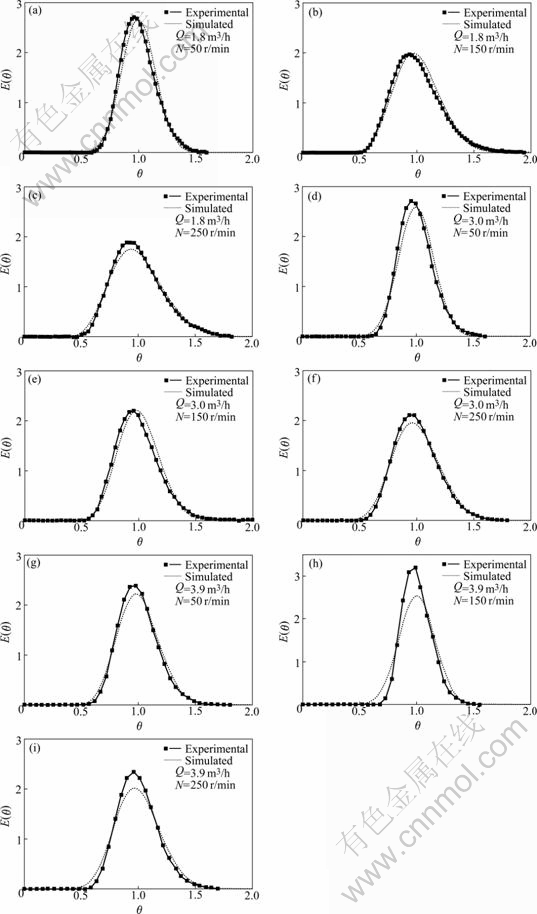
Fig.7 shows the experimental RTD curves in the traditional tubular reactor at inlet flow rate of 1.8 m3/h, and Fig.8 shows the numerical RTD curves at different impeller speeds. Several maximums of the curve appear with no stirring by experiment, while only one maximum by CFD prediction. The result is optimized by model simplification for interface between tubes on simulation. By comparing with no stirring, the RTD curve is narrow with stirring, where the flow is shown to approach to plug flow conditions. Although slow stirring can narrow the RTD curve and improve the performance of the reactor, increasing impeller speed widens the RTD curve. Maximum of E(θ) offsets to θ<1 at impeller speed of 400 r/min, indicating the presence of the short- circuits. High impeller speed can worsen reactor performance. The maximum of the curve E(θ) appears near θ=1 at impeller speed of 50 r/min, and flow pattern tends to ideal plug flow.
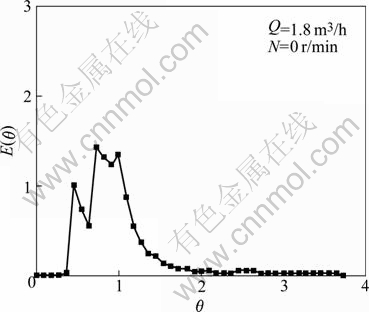
Fig.7 Experimental RTD curves in traditional tubular reactor at inlet flow rate of 1.8 m3/h
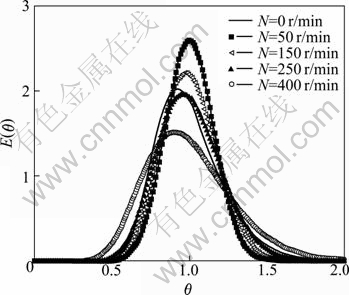
Fig.8 Typical RTD curves at different impeller speeds at inlet flow rate of 1.8 m3/h
Table 1 shows the comparison between simulated and experimental data of mean residence time and variance. For existing error and model simplification, numerical prediction is a little lower in mean residence
Table 1 Comparison between numerical and experimental data of mean residence time and variance
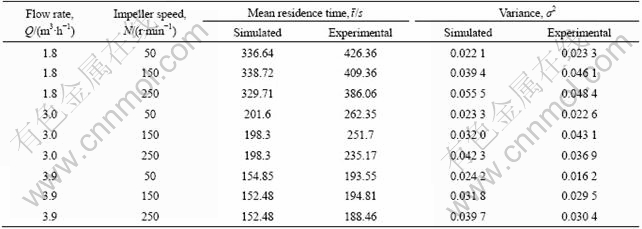
time. But the result shows a good agreement in the whole trend, which provides positive reference significantly. It can be seen form Table 1, as the inlet flow rate increases, the mean residence time and the variance of RTD decrease proportionally. As the rotation speed increases, the variance increases sharply, indicating that the fluid flow deviates from the ideal plug flow. There are several influencing factors of mean residence time. In CFD prediction, as the rotation speed increases, there is no evident effect on the mean residence time. But in experiments, the result shows that the mean residence time decreases with increasing rotating speed. For the centrifugal force generated by high rotating speed, circulation dead zone appears near wall surface of vessel and most fluid flows forward along stirring shaft to outlet directly. Moreover, as inlet flow rate increases, changing rotating speed brings no clear effect on the mean residence time.
5 Conclusions
1) The CFD simulation of flow field and RTD in a tubular stirred reactor using the standard k-ε turbulence model and MRF rotating model was investigated. The RTD curves predicted with CFD model show good agreement with experimental data.
2) The distribution of velocity shows that the flow field is very turbulent and the fluid flows along the shaft in helical shape. The velocity magnitude increases from shaft to the ends of impeller, and the higher the impeller speed is, the larger the gradient of velocities magnitudes.
3) The tubular reactor with a stirrer can improve the flow profile by narrowing the RTD curve, decreasing mean residence time and avoiding back mixing, but a high stirring speed broadens the RTD curve drastically. The optimum rotating speed is 50 r/min while inlet flow rate is 1.8 m3/h.
4) The RTD functions demonstrate that the profiles of flow approach to plug flow. As the flow rate increases, the mean residence time as well as the variance of RTD decreases proportionally. As the rotation speed increases, there is no evident effect on the mean residence time, whereas the variance is enlarged greatly.
References
[1] ZHANG Qi, JIN Jun-ze, WANG Tong-min, LI Ting-ju, GUO Qing-tao. Analysis of molten metal flow in rotating magnetic field [J]. The Chinese Journal of Nonferrous Metals, 2007, 17(1): 98-104. (in Chinese)
[2] SWAINE D E, DAUGULIS A J. Review of liquid mixing in packed bed biological reactors [J]. Biotechnol Prog, 1998, 4: 134-148.
[3] RANADE V V, DOMMETI S M S. Computational snapshot of flow generated by axial impellers in baffled stirred vessels [J]. Trans IChemE, 1996, 74(4): 476-484.
[4] STAMOU A I. Improving the hydraulic efficiency of water process tanks using CFD models [EB/OL]. Chemical Engineering and Processing, 2007, doi:10.1016.
[5] TORRE J P, FLETCHER D F, LASUYE T, XUEREB C. Single and multiphase CFD approaches for modelling partially baffled stirred vessels: Comparison of experimental data with numerical predictions [J]. Chemical Engineering and Science, 2007, 62: 6246-6262.
[6] DARELIUS A, RASMUSON A, van WACHEM B, NIKLASSON I, FOLESTAD S. CFD simulation of the high shear mixing process using kinetic theory of granular flow and frictional stress models [J]. Chemical Engineering Science, 2008, 63: 2188-2197.
[7] PAKZAD L, EIN-MOZAFFARI F, CHAN P. Using electrical resistance tomography and computational fluid dynamics modeling to study the formation of cavern in the mixing of pseudo plastic fluids possessing yield stress [J]. Chemical Engineering Science, 2008, 63: 2508-2522.
[8] OCHIENG A, ONYANGO M S, KUMAR A, KIRIAMITI K, MUSONGE P. Mixing in a tank stirred by a Rushton turbine at a low clearance [J]. Chemical Engineering and Processing, 2008, 47: 842-851.
[9] ZHAO Qiu-yue, ZHANG Ting-an, CAO Xiao-chang, JIANG Xiao-li. RTD curves of tubular reactor with stirrer [J]. Journal of Northeastern University: Natural Science, 2006, 27(2): 206-208.
[10] DEGLON D A, MEYER C J. CFD modeling of stirred tanks: Numerical considerations [J]. Minerals Engineering, 2006, 19: 1059-1068.
[11] XIA J Y, WANG S J, ZHANG S L, ZHONG J J. Computational investigation of fluid dynamics in a recently developed centrifugal impeller bioreactor [EB/OL]. Biochem Eng J 2007, dio:10.1016/ j.bej.2007.08.006
[12] JAVED K H, MAHMUD T, ZHU J M. Numerical simulation of turbulent batch mixing in a vessel agitated by a Ruston turbine [J]. Chemical Engineering and Processing, 2006, 45: 99-112.
[13] GAVRILESCU M, TUDOSE R Z. Residence time distribution of the liquid phase in a concentric-tube airlift reactor [J]. Chemical Engineering and Processing, 1999, 38: 225-238.
[14] SAHLE-DEMESSIE E, BEKELE S, PILLAI U R. Residence time distribution of fluids in stirred annular photo reactor [J]. Catalysis Today, 2003, 88: 61-72.
[15] KUMAR V, NIGAM K D P. Numerical simulation of steady flow fields in coiled flow inverter [J]. International Journal of Heat and Mass Transfer, 2005, 48: 4811-4828.
Foundation item: Project(20050145029) supported by the PhD Program Foundation of Ministry of Education of China; Project supported by the Foundation of Excellent Talents of Science and Technology of Liaoning Province, China
Corresponding author: ZHANG Ting-an; Tel: +86-24-83687715; E-mail: zta2000@163.net
DOI: 10.1016/S1003-6326(08)60301-5
(Edited by YANG Bing)