高速电主轴非接触电磁加载研究
周训通，刘宏昭，邱荣华, 刘丽兰，原大宁
(西安理工大学 机械与精密仪器工程学院，陕西 西安，710048)
摘要：为了克服接触式加载中存在的摩擦、振动、噪声等问题，提出应用电磁加载的方法，研制电主轴非接触加载试验平台，进行电主轴非接触加载试验。推导加载装置的吸引力公式，通过磁路分割法计算加载力，并进行有限元仿真计算。通过力传感器采集电磁铁不同输入电流下的加载力，并与理论计算值和有限元仿真值进行对比，验证非接触加载的正确性和可行性；在恒定输入电流情况下，电主轴不同转速时进行电磁铁加载力的测试，得出加载力与转速的关系曲线。研究结果表明：计算值、仿真值与实测值比较接近，说明实验装置设计正确。本实验平台可准确高效采集加载力、温度等信息。
关键词：高速电主轴；非接触；电磁力；有限元法
中图分类号：TM306 文献标志码：A 文章编号：1672-7207(2013)07-2756-08
Non-contact loading of high speed motorized spindle
ZHOU Xuntong, LIU Hongzhao, QIU Ronghua, LIU Lilan, YUAN Daning
(School of Mechanical and Instrumental Engineering, Xi’an University of Technology, Xi’an 710048, China)
Abstract: To overcome the existing problems in the contact-loading, such as friction, vibration and noise, the method of loading by the electromagnet was put forward. Motorized spindle non-contact loading test platform was developed. The attractive force formula of the loading device was deduced. The loading force value was theoretically calculated by division of magnetic path and simulated by FEM. Loading forces in different input current of electromagnet were collected. Comparing theoretically calculated and simulated values with actual load collected by experiments, the correctness and feasibility of non-contact loading was verified. Data acquisition of loading forces in different speed of motorized spindle was carried out, and the forces and loading speed relation curve were deduced. The results show that the calculated values and simulation values are close to measured results, which indicates that the test platform is designed correctly. The test platform can accurately capture the efficiency loading force, temperature and so on.
Key words: high speed motorized spindle; non-contact; electromagnetic force; finite element method
以高切削速度、高进给速度、高加工精度为主要特征的高速加工技术是继数控技术之后，使制造技术产生第二次革命性飞跃的一项高新技术[1]。数控机床以及加工中心中的核心部件是高速电主轴，高速电主轴的性能直接影响加工的精度和生产效率。目前，电主轴作为高速机床的主轴部件，其设计不仅需要全面真实的外载荷依据而且需要建立电主轴载荷谱[2]，因此电主轴的加载试验对于研究电主轴的动态性能、可靠性以及设计研发等都具有十分重要的意义。加载试验比空载试验更能准确反映电主轴的实际工况，尤其是需要在电主轴实际加工工况中建立的载荷谱的指导下加载，才能更准确地反映电主轴的可靠性及动态性能[2]。传统的电主轴的加载试验有切削力法、转矩转速仪法以及液压加载法。这些方法只适合于中低速运转，当高速运转时，会产生剧烈摩擦热、振动和噪声而不能长时间运行，因而达不到预期的实验效果。在国内，孟杰等[3-5]采用的高速电主轴的加载方法为对拖式加载法，即电主轴与测功机通过联轴节相连接，测功机为电主轴提供负载转矩的加载方式，然而测功机与电主轴之间必然存在一定的偏心量，当电主轴高速旋转时会产生剧烈振动，而且这种方式只能模拟负载转矩，无法模拟电主轴受到的径向力。在此，本文作者针对上述问题，开发了高速电主轴非接触加载试验装置，可以实现电主轴的非接触加载以及加载力的测试[6]，并对加载电磁力进行了理论计算、有限元仿真和加载力实测。
1 实验台的构成及加载原理
根据电主轴可靠性实验的需要，针对某型号电主轴开发了一种非接触电磁加载装置，如图1所示。
图1 非接触加载实验平台
Fig.1 Non-contact loading experiment platform
本装置加载及测试原理图如图2所示，主要由6部分组成：
(1) 电磁加载装置：电磁铁、铁镍合金导磁盘；
(2) 电主轴及固定部分：电主轴、固定座；
(3) 传感器部分：S型拉压力传感器、温度传感器、振动传感器、位移传感器、变送器；
(4) 信号采集部分：多路信号采集仪；
(5) 电源：24 V电源、可调直流恒流源；
(6) 显示部分：计算机。
其加载原理为：直流恒流源给电磁铁线圈供电，调节电流可以改变磁场强度，进而改变加载力。电磁铁线圈通直流电会产生一个闭合磁场。其磁路为：电磁铁铁芯—气隙Ⅰ—加载盘—气隙Ⅱ—电磁铁铁芯。电磁铁加载装置如图3所示。该磁场可以对高导磁率的铁镍合金加载盘产生麦克斯韦吸引力，该力可以模拟电主轴受到的径向力[7-8]。电磁铁主要参数如表1所示。
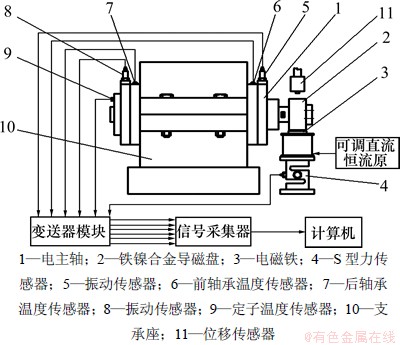
图2 非接触加载实验台结构示意图
Fig.2 Schematic drawing of non-contact loading experiment platform
该加载装置具有以下优点：
(1) 采用非接触电磁加载，避免了接触加载产生的高热量、振动及噪声。
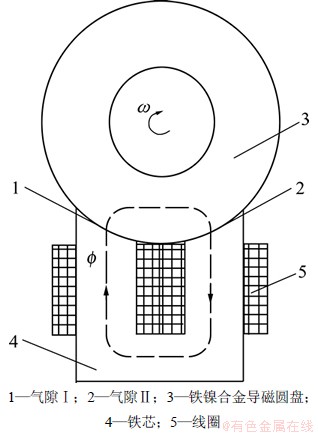
图3 电磁铁加载装置示意图
Fig.3 Scheme of electromagnet loading devices
表1 电磁铁主要参数
Table 1 Major parameters of electromagnet
(2) 电磁加载装置中的电磁铁端面处为圆弧形结构。通过线切割的方法将铁芯硅钢片上端面加工成圆弧面以配合电主轴端部导磁盘的外表面，使铁芯端面与铁镍合金导磁盘的间隙保持均匀气隙，既能保证穿出磁感线的均匀性，又能保证尽可能少的漏磁以达到最大加载力。
(3) 电主轴端部装有高导磁率铁镍合金导磁盘，铁镍合金具有很高的导磁率和很小的矫顽力[9]，因此在电磁场中能产生较大的麦克斯韦力。
(4) 本加载装置的气隙可以通过底部安装的调隙螺栓调节气隙改变电磁力。
(5) 电磁加载装置底部安装有2个S型拉压力传感器，可以实时测得加载力。
2 加载力的理论计算
由于本加载装置采用的是电磁加载的方式，因此需要用相关的电磁场理论计算加载力。电磁场理论是由一套麦克斯韦方程组来描述的，以该方程组为基础可以推导出麦克斯韦吸引力公式，该吸引力可作为电主轴的径向加载力。本装置的吸引力来源于气隙与铁镍合金的导磁率不同，铁镍合金导磁率远高于空气导磁率，因此，在铁镍合金导磁盘下表面法向方向会产生张量力[10]，即麦克斯韦吸引力。考虑到磁性材料的非线性以及磁场的空间复杂性，精确的理论计算是很困难的。
由于结构及原理的相似性，本电磁加载装置加载力的计算参照磁力轴承的设计及计算方法。通常在简化设计的基础上采用近似的分析方法，特作如下假设：
(1) 在电磁铁、导磁圆盘转子和气隙中磁场是分段均匀的。
(2) 铁芯呈不饱和特性。
(3) 除气隙外，磁通全部通过铁芯，不考虑漏磁和磁滞的影响。只要铁芯的磁感应强度远低于饱和磁感应强度，磁场特性就可以按基本磁化曲线计算。
当电磁铁与导磁盘转子的气隙很小时，能够很好地满足以上3个假设[11]。为了保证加载能产生足够大的径向加载力以及保证运转安全，取气隙为0.5 mm。
2.1 吸引力公式的推导及加载力的计算
本电主轴非接触加载实验台的核心部分是电磁加载装置，其简化模型如图4所示。
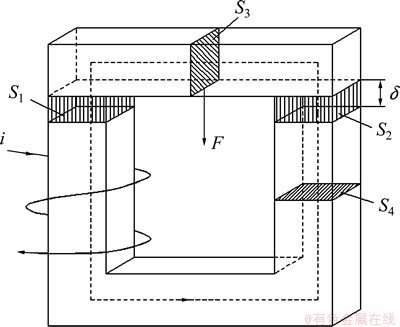
图4 电磁加载简化模型
Fig.4 Simplified model of electromagnetic loading
该型号电主轴加工工件时的平均径向力大约为80 N，为了保证加载力足够大，设初始加载力为160 N。麦克斯韦吸引力公式：
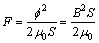(1)
式中：F为麦克斯韦力；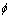
为磁通；B为磁感应强度；S为电磁铁端面面积；μ0为真空磁导率。
由于本装置的U型电磁铁有2个端面，由式(1)得出本例中电磁铁与导磁盘转子间的吸引力(即加载径向力)为：
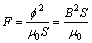(2)
磁感应强度公式：
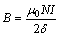(3)
式中：δ为电磁铁端面与导磁圆盘气隙厚度；N为电磁铁线圈匝数；I为线圈中电流。
根据磁路安培环路定律，对图4中分段均匀磁路有：
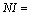
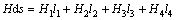(4)
式中：H为磁场强度；s为磁感应线穿过的面积；H1为气隙Ⅰ磁场强度；H2为气隙Ⅱ磁场强度；H3为导磁盘段磁场强度；H4为电磁铁铁芯磁场强度；l1 为气隙1厚度；l2为气隙2厚度；l3为导磁盘段磁路长度；l4为电磁铁铁芯磁路长度。
由磁场强度公式：
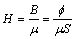(5)
则：
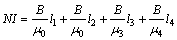
式中：μ3为铁镍合金导磁率；μ4为电磁铁铁芯导磁率。
令l1=l2=δ，则
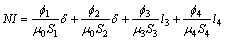
式中：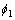
，
，
，
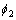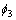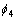分别为气隙Ⅰ、气隙Ⅱ、导磁盘段和铁芯段磁路的磁通量，S1，S2，S3，S4分别为气隙Ⅰ、气隙Ⅱ、导磁盘段和铁芯段磁路的端面面积。忽略漏磁，并近似地
(6)
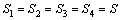(7)
将式(6)和(7)代入式(5)，整理得：
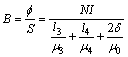(8)
由于铁镍合金导磁盘和电磁铁铁芯均采用磁性材料，具有很高的导磁率，远远大于空气导磁率，即
＞＞ 
，
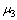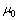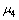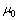＞＞，则式(8)可近似为
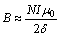(9)
将式(9)代入式(2)得：
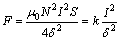(10)
式中：
。
当电磁加载装置结构参数一定时，k为常数。因此，麦克斯韦吸引力与线圈电流的平方成正比，与气隙厚度的平方成反比。由于各种误差的存在，模型与实际情况存在着差异，其中铁芯磁阻的影响为主。如果忽略铁芯磁阻误差，理论上建立的电磁加载系统数学模型与实际系统较接近。研究表明，建模误差对系统的设计和稳定性产生的影响可以忽略[11]。因此，可以得出结论：当结构参数已定时，可以通过改变电流及气隙来改变加载力。式(10)为电磁加载装置的吸引力计算公式，以此为基础可以进行电磁加载装置结构设计与分析。
电磁铁线包匝数N=9 000匝，铁芯横截面积S=8 cm2，δ=0.5 mm，当输入直流电流I=0.044 A，由式(10)计算得导磁盘受到的总径向力为F=159.25 N，接近初始设计值160 N。
图5所示为加载力与输入电流、气隙的关系。从图5可以看出：加载力与输入电流平方成正比，与气隙厚度的平方成反比。
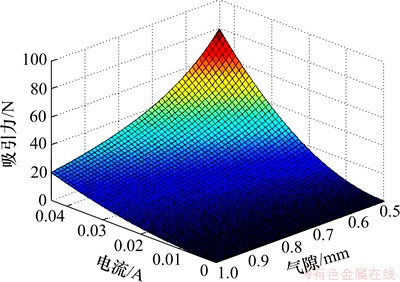
图5 输入电流、气隙与加载力的关系
Fig.5 Relationship of input current, air gap and loading force
本电磁加载装置励磁为直流恒流源，可以通过调节电流改变加载力；调节电磁加载装置底部调隙螺栓改变气隙也可以改变电磁加载力。但是精确计算时，要考虑漏磁系数Kf，式(10)可以写为：
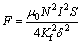(11)
漏磁系数Kf取值由磁路组成决定，根据磁路设计优劣差别很大，可在1~10范围变化，该值的选取带有较大的经验性[12]。
2.2 磁路分割法计算加载力
和电路一样，磁路也存在串联和并联磁路，较为精确地计算磁路各处磁导可以采用磁路分割法[12]，通过磁路分割法计算的加载力可以与上文中加载力计算值进行对比。
将加载装置的整个磁路分割为气隙Ⅰ段、气隙Ⅱ段、导磁盘段和铁芯段，各部分属于串联关系如图6所示，其中，Rm1，Rm2，Rm3，Rm4分别为气隙Ⅰ、气隙Ⅱ、导磁盘和铁芯的磁阻，其计算方法可按式(12)计算：
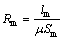(12)
式中：lm为各段磁路长度；μ为各部分磁导率；Sm为各段磁路横截面积。
各段磁路的磁阻如表2所示。
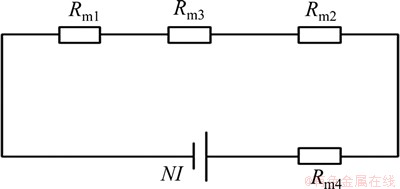
图6 磁路示意图
Fig.6 Magnetic circuit schematic diagram
表2 分割磁路计算得到的各部分磁阻
Table 2 Division for calculation of magnetic circuit in every part of magnetic resistance
由表2可以看出：气隙的磁阻远大于铁镍合金导磁盘和铁芯的磁阻。当线圈为9 000匝，输入电流为0.044 A时，可得磁路磁通为：
Wb
将上述参数带入式(2)得：
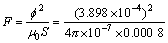=151.1 N
3 电磁力有限元仿真计算
有限元方法能够考虑磁性材料的非线性特征，可以较为精确地计算漏磁效应以及整个磁路空间的磁场分布[13]。为了证明理论计算结果的正确性，可以利用有限元仿真软件进行求解、比对。
3.1 模型的建立以及网格的划分
电磁加载装置是对称结构，取结构的1/2进行建模，其被空气层包围。首先，选取磁场分析专用单元SOLID96，建立装置模型，赋予空气层、铁芯、导磁圆盘及空气层各部分材料属性，分别输入铁镍合金以及硅钢片的B-H磁化曲线，整体模型建立如图7所示。
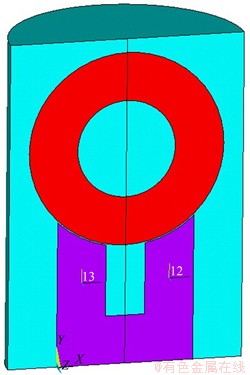
图7 电磁加载装置实体模型
Fig.7 Model of electromagnetic loading device
由于模型结构并不复杂，调整网格划分精度等级后，采用自由网格划分。由于导磁圆盘受到吸引力，因此给导磁圆盘施加受力标志。根据线圈的实际形状和尺寸建立线圈，输入线圈匝数N=9 000匝，电流I=0.044 A，模型网格划分如图8所示。
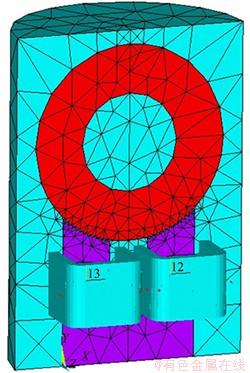
图8 模型网格划分
Fig.8 Hyper mesh of loading model
3.2 加载求解及处理结果
在模型外表面施加通量平行条件，将导磁圆盘生成一个组件，并施加受力标志。给铁芯底部坐标系原点处的节点施加约束，即使该点磁矢量为0。
导磁盘作为受力体并求解，得到磁感应强度云图及矢量图如图9和10所示。可以看出：电磁铁铁芯端面尖峰处磁通密度最大，因此，电磁铁端面对应的导磁盘下表面处吸引力最大，导磁圆盘整体受到了一个竖直向下的吸引力。
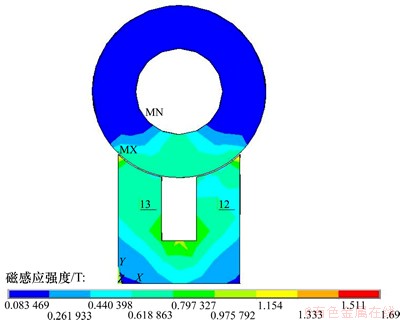
图9 磁感应强度云图
Fig.9 Cloud chart of magnetic flux density
图10 磁感应强度矢量图
Fig.10 Vector diagram of magnetic flux density
有限元软件求解结果如表3所示。可以看出，通过有限元仿真求解得出导磁盘Y方向(竖直方向)受力值为-79.438 N，负号代表受力竖直向下。导磁盘X轴和Z轴方向受力由于是左右对称互相抵消。由于该有限元模型为实际结构的1/2，因此整体实际受力为79.438 N的2倍，即158.88 N，该值与吸引力公式计算值159.25 N和磁路分割法计算值149.62 N相比非常接近。
表3 加载力求解结果
Table 3 Solution results of loading force
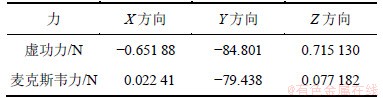
3.3 理论计算值、仿真值和实测值的对比
本实验台的电磁加载装置通以直流电进行加载后，可以通过多路信号采集器实时采集S型拉压力传感器所测得的加载力。
在电主轴静止时分别对电磁铁通电流为0.02，0.03，0.04，0.05，0.06，0.07 A直流电，气隙为0.5 mm，分别通过吸引力公式法、磁路分割法、有限元仿真法对加载力进行计算，并与采集到的实测值进行了对比，结果如表4所示。图11所示分别为这3种计算方法与实测值的对比曲线。
表4 加载力计算、仿真与实测值对比
Table 4 Contrast of loading force calculation, simulation and measured value
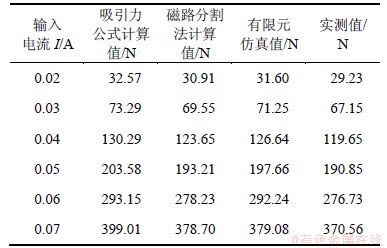
由图11可以看出：由本装置加载力式(10)理论计算的加载力偏离实际值最大，而磁路分割法和有限元仿真法计算值比较接近实测值，偏差在5%以内。对于本加载装置加载力式(10)要考虑漏磁系数，则按式(11)取漏磁系数Kf=1.05，此时比较接近实际值。由此可知：本电磁加载装置设计、计算是正确的。
4 不同转速加载力测试
在恒定电流下为电磁铁供电进行加载，在电主轴不同转速下测试加载力变化。
主要试验装置为S型拉压力传感器、变送器、配套信号采集系统及软件。
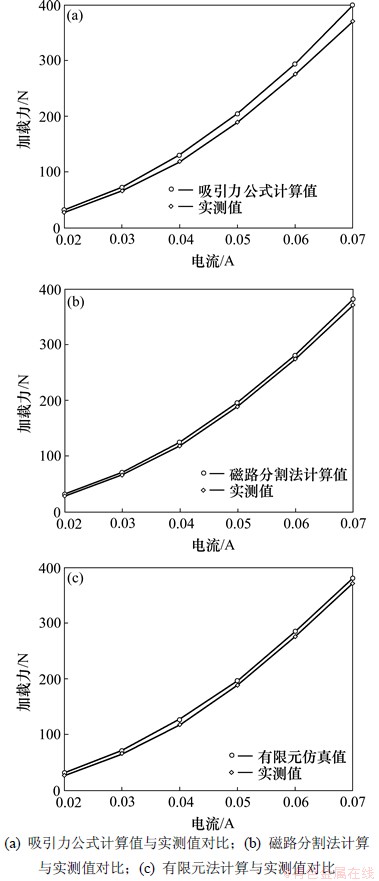
图11 吸引力公式计算、磁路分割法计算、有限元仿真和实测值对比
Fig.11 Comparison of attractive force formula value, separation method of magnetic circuit, finite element simulation value and measured value
当电主轴静止，即转速为0 r/min时，给电磁铁通恒定直流电，使加载力达到120 N。在电磁铁输入电流不变的情况下，分别在转速1 500，3 000，4 500，6 000，7 500，9 000 r/min时通过拉压力传感器测加载力，测试值如表5所示。其测试值的拟合曲线如图12所示。
表5 不同转速加载力测试值
Table 5 Loading force test values at different speeds
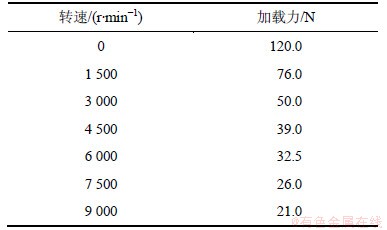
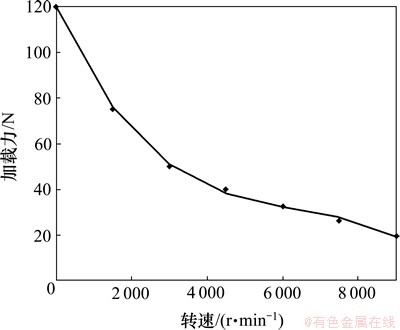
图12 不同转速加载力测试值拟合曲线
Fig.12 Fitting curve of loading force test values at different speeds
在实测过程中，当转速不断升高时，加载力呈非线性减小。这是由于导磁盘切割磁感线产生涡流，导致径向加载力减小，涡流的磁场会抵消一部分电磁场磁场，使总磁场强度变小[14-15]。可以通过加大电磁铁线圈输入电流来达到指定加载力，从而解决加载力变小的问题。
因此，在下一步工作中，动态加载时涡流的分析、转速—加载电流—加载力间关系的分析和计算、涡流产生的切向洛伦兹力的计算和测试是重点。
5 结论
(1) 克服了传统接触式加载中遇到的摩擦生热、振动以及噪声等问题，推导出本加载装置吸引力的公式，通过磁路分割法和有限元仿真法进行了加载力计算，对加载实测值进行了采集，计算值与实测值比较接近，从而验证了设计的正确性及可行性。
(2) 本实验平台可以准确、高效的实时采集、记录加载力、温度、振动、轴端跳动量等各种信号，为后续的可靠性实验提供数据。
参考文献：
[1] 储开宇. 数控高速电主轴技术及其发展趋势[J]. 机床与液压, 2006(10): 228-230.
CHU Kaiyu. Technology and developing trends for high-speed electronic spindle of NC machine tools[J]. Machine Tool & Hydraulics, 2006(10): 228-230.
[2] 黄广祖, 赵钦志, 盛伯浩, 等. 加工中心可靠性试验载荷谱的研究[J]. 制造技术与机床, 2008(2): 60-65.
HUANG Guangzu, ZHAO Qinzhi, SHENG Bohao, et al. Research on the loading chart for reliability testing of machining center[J]. Manufacturing Technology and Machine Tool, 2008(2): 60-65.
[3] 孟杰. 高速电主轴动力学分析与实验研究[D]. 重庆: 重庆大学机械工程学院, 2008: 81-85.
MENG Jie. Dynamic analysis and experimental study on high speed motorized spindle[D]. Chongqing: Chongqing University. School of Mechanical Engineering, 2008: 81-85.
[4] 王永宾. 电主轴综合性能测试与评价系统的研究[D]. 北京: 北京工业大学机电学院, 2009: 13-23.
WANG Yongbin. Motorized spindle comprehensive performance test and evaluation system[D]. Beijing: Beijing University of Technology. Mechanical Engineering and Application of Electronic Technology Institute, 2009: 13-23.
[5] 孟杰, 陈小安, 康辉民, 等. 高速电主轴加载试验的研究[J]. 机械强度, 2009, 31(4): 687-692.
MENG Jie, CHEN Xiaoan, KANG Huimin, et al. Study on dynamic loading experiment of high speed motorized spindle[J]. Journal of Mechanical Strength, 2009, 31(4): 687-692.
[6] 刘宏昭, 邱荣华, 周训通, 等. 一种高速电主轴非接触电磁加载装置. 中国: 201010589402.1[P]. 2010-06-29.
LIU Hongzhao, QIU Ronghua, ZHOU Xuntong, et al. A high-speed motorized spindle none-contact loading device. China: 201010589402.1[P]. 2010-06-29.
[7] 张斌, 胡业发, 丁国平, 等. 径向磁力轴承涡流损耗分析与计算[J]. 机械制造, 2007, 45(515): 36-38.
ZHANG Bin, HU Yefa, DING Guoping, et al. Radial magnetic bearing the loss of the eddy analysis and calculation[J]. Machinery, 2007, 45(515): 36-38.
[8] 黄德中. 圆弧形混合磁悬浮轴承的研究[J]. 农业机械学报, 2003, 34(4): 133-136.
HUANG Dezhong. Study on arc bearing of mixed magnetic suspension[J]. Transactions of the Chinese Society for Agricultural Machinery, 2003, 34(4): 133-136.
[9] 曹静, 王永锋. 退火方式对1J79软磁合金磁性能的影响[J]. 材料热处理技术, 2008, 37(20): 82-89.
CAO Jing, WANG Yongfeng. Influence of annealing process on magnetic properties of 1J79 alloy[J]. Hot Working Technology, 2008, 37(20): 82-89.
[10] Ulaby F T. Fundamentals of applied electromagnetics fourth edition[M]. America: Pearson Education Asia Ltd, 2004: 225-237.
[11] 胡业发, 周祖德. 磁力轴承的基础理论与应用[M]. 北京: 机械工业出版社, 2006: 17-24.
HU Yefa, ZHOU Zude. The basic theory and application of magnetic bearings[M]. Beijing, Mechanic industry Press, 2006: 17-24.
[12] 娄路亮, 王海洲. 电磁阀设计中电磁力的工程计算方法[J]. 导弹与航天运载技术, 2007(1): 40-45.
LOU Luliang, WANG Haizhou. Methods of electromagnetic force calculation for engineering application[J]. Missiles and Space Vehicles, 2007(1): 40-45.
[13] 安琳, 刘志珍, 赵琳. 电磁阀的有限元法磁场分析及吸力计算[J]. 山东大学学报: 工学版, 2004, 34(6): 27-31.
AN Lin, LIU Zhizhen, ZHAO Lin. Magnetic field analysis and electromagnetic force calculation for electromagnetic valves based on finite element method[J]. Journal of Shandong University: Engineering Science, 2004, 34(6): 27-31.
[14] 曹广忠, 虞烈, 谢友柏. 实心转子—电磁轴承系统的损耗分析[J]. 航空动力学报, 2003, 18(1): 124-129.
CAO Guangzhong, YU Lie, XIE Youbai. Rotating loss analysis for active magnetic bearing with solid rotating rotor[J]. Journal of Aerospace Power, 2003, 18(1): 124-129.
[15] Muramatsu K, Shimizu T, Kameari A, et al. Analysis of eddy currents in surface layer of laminated core in magnetic bearing system using leaf edge element[J]. IEEE Transaction on Magnetics, 2006, 42(4): 881-889.
(编辑 赵俊)
收稿日期：2012-07-15；修回日期：2012-10-10
基金项目：国家科技重大专项(2010ZX04014-012)；陕西省自然科学基金资助项目(2012JQ7011)
通信作者：刘宏昭(1954-)，男，山西代县人，教授，博士生导师，从事机电系统建模、测试及控制、机构学及CAD、机械动力学研究；电话：13629276809；E-mail: liu-hongzhao@163.com
