文章编号：1004-0609(2011)01-0205-09

基于有限元模拟的20/316L双金属复合管拉拔参数的优化

陆晓峰, 郑 新

 (南京工业大学 机械与动力工程学院，南京 210009)

摘 要：借助有限元软件ABAQUS6.5模拟研究20碳钢作基管、316L不锈钢作内衬管的双金属复合管的拉拔成形过程，分析稳定拉拔阶段成形区内轴向、径向和环向应力的分布，找出拉拔后衬管出现横裂、纵裂及模具受磨损的原因，探讨拉拔力和内外管间残余接触压力的分布规律。通过正交实验法进一步研究拉拔参数(模具锥半角α、过渡圆弧半径r、定径带长度l、摩擦因数μ、拉拔速度v、模具直径d)对拉拔20/316L双金属复合管的影响，采用极差和方差分析法对模拟结果进行分析，得到复合管在最大残余接触压力条件下的最优拉拔工艺参数(α=11?、r=3 mm、l=7 mm、μ=0.05、v=0.03 m/s、d=17.3 mm)及各因素对分析指标的影响规律。在此基础上对优化方案进行数值模拟，模拟结果表明了正交实验对拉拔复合管参数优化的有效性。应用拉拔试验表明，参数优化后的硬质合金拉拔模具的工作寿命比未优化前硬质合金模具的工作寿命高出6倍。

关键词：双金属复合管；数值模拟；残余接触压力；正交实验法；拉拔参数；优化

中图分类号  TG356.23  TG356.5　　     文献标志码：A

Optimization of drawing parameters for 20/316L bimetal-lined pipe based on FEM simulation

LU Xiao-feng, ZHENG Xin

(College of Mechanical and Power Engineering, Nanjing University of Technology, Nanjing 210009, China)

Abstract: By means of the finite element analysis software ABAQUS6.5, a drawing forming process of bimetal-lined pipe made of 20 carbon steel as the base tube and 316L stainless steel as the liner tube was simulated to analyze the axial, radial and hoop stress distributions in the forming zone during the stable drawing stage. The reasons of transverse and longitudinal crack on the liner tube and die wear were found. The distributions of drawing force and residual contact pressure between the inner and outer pipe were discussed. The effects of drawing parameters(the semi-angle of drawing dies α, the transition arc radius r, the length of bearing part l, the friction coefficient μ, the drawing velocity v, the diameter of drawing dies d)on drawing 20/316L composite tube were investigated by using orthogonal experiment. The optimal drawing parameters (α=11?, r=3 mm, l=7 mm, μ=0.05, v=0.03 m/s, d=17.3 mm) under the maximum residual contact pressure and the influence of factors on analysis indexes were obtained according to the simulation results by the methods of range analysis and variance analysis. Then the drawing process was further studied by using these optimal parameters, and the results confirmed the effectiveness of the orthogonal experiment on optimization of drawing composite tube parameters. Compared with the non-optimized parameters cemented carbide drawing dies，the application experiment result shows that the working lifetime of the optimal cemented carbide drawing die can be increased 6 times.

Key words: bimetal-lined pipe; numerical simulation; residual contact pressure; orthogonal experiment method; drawing parameter; optimization

随着能源危机的日益迫近，炼制劣质原油已成为炼油行业必须面对的问题，随之而来的腐蚀问题也常常会给安全生产带来很大隐患。以某100万吨加氢裂化装置8台高压空冷器为例，在现有的原料及工艺条件下，使用20^#钢管束的高压空冷器，其使用寿命仅1年左右，如果改用Incoloy825管束，其寿命虽增加，但造价大约增至20^#钢管束的10倍，巨额的投资成本，使企业面临两难的抉择。为此开发内衬316L双金属复合管用于上述高压空冷器上，可达到提高使用寿命、降低成本的目的。

双金属复合管拉拔成形是非常复杂的弹塑性变形过程，既有物理非线性，又有几何非线性，而且边界条件往往也很复杂^[1-3]，因而使得拉拔成形双金属复合管的理论研究十分困难，国内学者仅秦建平等^[4-5]和杨贵平等^[6]对双金属复合管空拉成形过程作了一些探索性理论分析。随着计算机技术的发展，基于有限元法的数值模拟在金属塑性成形中得到广泛应用^[7-8]。国外ALCARAZ等^[9]利用有限元法对高温挤压复合双金属管成形进行数值模拟，得到了不同参数对复合管挤压成形的影响；BERSKI等^[10]基于有限元法分析了铝棒套在铜管里通过爆炸复合双金属棒的成形过程，研究了模具形状和挤压比对挤压成形的影响；国内臧新良等^[11]采用大变形弹塑性有限元法，针对空拔双金属复合管的冷成形工艺进行了数值模拟研究；杜清松等^[12]针对液压复合双金属管的塑性成形过程进行了有限元模拟；杜艳梅等^[13]对Al/Mg双层复合管热挤压过程进行了数值模拟分析；而目前国内外有关内衬316L不锈钢复合管冷拔过程的有限元模拟及拉拔工艺参数优化研究尚未见报道。

本文作者利用有限元软件ABAQUS6.5对内衬316L不锈钢复合管的整个拉拔过程进行模拟，得到稳定拉拔阶段轴向、径向和环向应力的分布，找出拉拔完成后复合管衬管内壁出现横裂、衬管外壁出现纵裂及模具磨损的原因；探讨了拉拔力和内外管间残余接触压力的分布规律，通过正交实验分析，得到在残余接触压力最大及拉拔力最小条件下的最优拉拔工艺参数，并据此优化方案进行数值模拟和拉拔试验，以上研究对于保证拉拔复合管产品质量、提高生产效率及延长模具寿命具有指导意义。

1  弹塑性有限元的基本理论

1.1  基本原理

图1所示为拉拔复合管几何模型示意图。由图1可见，衬管的变形区分为定径带区Ⅰ和拉拔扩径区Ⅱ，α是模具锥半角，r为工作锥与定径带处过渡圆弧半径，l为定径带长度，d为拉拔模具的定径带区直径。T₁、N₁为衬管在定径带区所受的摩擦力及正压力。拉拔过程中，模具在拉拔力的作用下逐渐与衬管相接触，衬管在拉拔模具挤压下产生径向扩径及轴向伸长，拉拔模具进入定径区后，衬管产生弹塑性变形，受到模具的正压力及切向摩擦力的作用。

图1  拉拔成形复合管示意图

Fig.1  Schematic illustration of drawing forming pipe

拉拔复合管成形过程是一个多重非线性耦合问题，既有几何非线性,又有接触和边界非线性,因此在模拟过程中要将各种非线性因素均考虑在内。

本研究主要采用虚功方程:

                                   (1)

式中：U为虚应变能；V为外力所做的虚功。

在ABAQUS/Explicit中应用Newton-Raphson算法获得非线性问题的解答，采用增量加载法，Newton-Raphson法的迭代公式：

            (2)

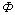式中：为位移增量，为第n次迭代的切线刚度; 为质点位移；R为增量载荷；P 为外载。

对于拉拔等金属塑性成形问题，由于其高度非线性，可引入收敛因子，获得改进的牛顿法。令：，利用有限元方法模拟金属塑性成形问题时，常采用小于1的收敛因子(称为衰减因子)进行修正^[14-15]。

1.2  摩擦属性的定义

复合管拉拔成形时，衬管变形是在与模具接触状态下进行的，模具通过其接触表面把力和速度的作用施加在衬管内壁上，使之产生塑性变形。因此，接触边界条件的处理对数值模拟分析有重要影响。拉拔成形过程的接触问题需要计算模具与衬管、衬管与基管的摩擦，考虑到摩擦力与相对滑动速度之间的关系以及提高有限元数值模拟的稳定性，本研究采用修正的库仑摩擦模型^[16]：

                        (3)

式中：μ为摩擦因数，f_n为法向接触力，V_r为接触点处衬管与模具表面的相对滑动速度，d′为介于10^-2~10^-4之间的常数^[17]。

2  复合管拉拔有限元计算

2.1  模型建立及模拟参数设定

在不考虑钢管偏心、壁厚不均的情况下，将双金属复合管的拉拔成形按轴对称问题处理。

2.1.1  建立几何模型

建立的有限元模型如图2所示，碳钢基管为d25 mm×3 mm、不锈钢衬管为d18 mm×1 mm、模具锥半角α=10?、过渡圆弧半径r=6、定径带长度l=8 mm、摩擦因数μ=0.1、拉拔速度v=0.05 m/s、模具直径d=17.4 mm。

图2  内衬316L复合管拉拔有限元模型

Fig.2  FE model of lined 316L composite tube in drawing

2.1.2  定义材料模型

衬管316L及基管20^#碳钢的基本力学参数如表1所示。在ABAQUS6.5软件中采用弹塑性硬化材料模型，此时应力是塑性应变的函数。在本实例中材料的初始屈服条件使用Mises屈服准则，拉拔模具假定为刚性体。实际拉拔过程中由于在衬管内加入润滑冷却液，使拉拔模具与衬管内壁摩擦引起的热效应很小，故定义材料属性时可不考虑弹性模量、屈服强度随温度的变化。

表1  复合管材料的力学性能

Table 1  Mechanical properties of pipe materials

2.1.3  单元选择及有限元网格划分

衬管及基管均采用双线性减缩积分轴对称四边形单元(CAX4R)。由于在成形过程中变形相对剧烈，为保证模拟的顺利进行和结果的相对准确性，在模拟中应用网格自适应技术^[18-19]，网格结构示意图如图3所示。

图3  有限元网格结构示意图

Fig.3  Schematic diagram of mesh structure of FE model

2.1.4  接触条件及摩擦属性的定义

拉拔成形过程的接触是边界条件高度非线性的复杂问题^[20]，对产生接触的两个物体必须满足无穿透条件。ABAQUS/Explicit提供的动态显示接触对算法可以很好地模拟拉拔模具和衬管、衬管与基管之间的接触关系。在模具与衬管的接触对中，主面为模具表面，从面是衬管内表面；在衬管与基管接触对中主面为基管内表面，从面为衬管外表面。在各个接触对中选用经典库伦摩擦，接触对之间的滑移选用有限滑移。

2.1.5  加载及求解

由于拉拔复合管的几何结构和成形过程中的受力状况均具有轴对称性,因此对内外管施加轴对称约束。对拉拔模具采用速度加载方式，将速度v=0.05 m/s加载到拉拔模具参考点RP上，加载采用Smooth step的幅值曲线，模拟求解过程选用ABAQUS/Explicit准静态分析。

2.2  数值模拟的结果与分析

2.2.1  轴向应力分析

图4所示为稳定拉拔阶段的轴向应力分布图。从图4可以看出，由于定径带区Ⅰ的衬管内、外表面摩擦状态和约束条件不同，使衬管内表面比外表面承受更高的轴向流动阻力，造成衬管壁厚方向上金属轴向流动不均，衬管截面的拉应力区约占壁厚的2/3，衬管内壁最大拉应力为569.5 MPa，而外壁存在较小的压应力。因此危险截面发生在定径带区Ⅰ模具与衬管相接触的部位，若此时拉应力过大，则促使内表面产生横向裂纹甚至被拉断，这是实际生产中复合管内壁产生横向裂纹的主要原因，从而严重影响拉拔后的管材质量。

图4  稳定拉拔阶段时的轴向应力

Fig.4  Axial stress of stable drawing

2.2.2  径向应力分析

图5所示为稳定拉拔时的径向应力分布图。由图5可知，复合管稳定拉拔时，其径向应力分布有两个应力集中区，分别在模具定径带区Ⅰ上端附近和拉拔扩径区Ⅱ起始处，衬管内壁与基管内壁都受较大的径向压应力，最大值为697.9 MPa，因此在这两个区域模具的磨损最快，可导致拉拔后的衬管壁厚不均匀、表面精度降低，最终导致拉拔模具失效。因此，为获得高质量的拉拔复合管、延长模具的寿命，对复合管拉拔成形的工艺参数优化是非常必要的。

2.2.3  环向应力分析

图6所示为复合管在稳定拉拔阶段的环向应力分布图。从图6可以看出，在定径带区Ⅰ处环向应力主

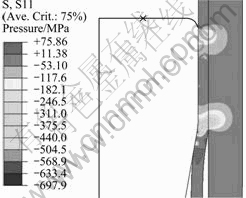
图5  稳定拉拔时的径向应力分布

Fig.5  Radial stress distribution of stable drawing

图6  稳定拉拔时的环向应力分布

Fig.6  Hoop stress distribution of stable drawing

要表现为压应力，衬管外壁为强压应力区，而且压应力影响1/2壁厚，从外壁到内壁逐渐减小，最大压应力为339.7 MPa；在拉拔扩径区Ⅱ处环向应力主要表现为拉应力，数值比较大，最大拉应力为444.8 MPa，而且对衬管的影响区域也较大，若此时环向拉应力过大，则促使衬管外壁产生纵向裂纹，从而影响复合管的使用质量。

2.2.4  残余接触压力分析

当拉拔模具拉出衬管后，基管弹性回复量大于衬管弹性回复量，两管之间的接触压力不足以使衬管产生反向屈服，只能耦合在一起，因此当拉拔完成后，内外管之间仍然接触，并产生残余接触压力p_rc。残余接触压力的大小是双金属复合管复合成形质量的一个重要指标，残余接触压力越大，结合强度越高，复合管的质量越好。图7所示为沿衬管外壁路径Path-1的残余接触压力变化曲线。由图7可知，拉拔完成后，内外管间残余接触压力趋于稳定，平均残余接触压力p_rc=16.3 MPa，远远大于《内衬不锈钢复合钢管》(CJ/T192—2004)规定的0.2 MPa。

2.2.5  拉拔力分析

图8所示为拉拔过程的拉拔力随加载时间的变化曲线。由图8可知，在拉过程中拉拔力的大小一直在变化，拉拔过程大致可以分为3个阶段，即初始拉入模具阶段、稳定拉拔阶段和拉出模具阶段。在初始拉入模具阶段，随着模具逐渐与衬管发生接触，拉拔力逐渐增大，对应图8中曲线开始时的拉拔力(绝对值)随时间快速增大的区段；稳定拉拔阶段随着拉拔模具与衬管完全接触，金属的流动渐趋稳定，拉拔力也趋于稳定，波动范围较小，对应图8中曲线的平直区段，可以把这个阶段拉拔力的平均值当作这次拉拔的拉拔力，由此，计算得到稳定拉拔阶段拉拔力f=7.828 kN；在拉出模具阶段，剩余钢管的长度变得很短，不足以发生一次预弯曲，拉拔力逐渐减小。

图7  内外管间的残余接触压力变化曲线

Fig.7  Changing curve of residual contact pressure of inner and outer pipe

图8  复合管成形过程的拉拔力变化曲线

Fig.8  Changing curve of drawing force of composite pipe forming process

3  复合管拉拔因素正交实验分析

3.1  实验因素选择

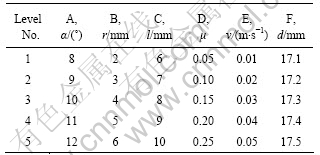
为保证拉拔后衬管发生塑性变形而基管处在弹性范围内，从而获得高结合强度(残余接触压力P_rc)的复合管以及延长模具的使用寿命，同时尽可能减少数值模拟次数，考察因素A—模具锥半角α、因素B—过渡圆弧半径r、因素C—定径带长度l、因素D—摩擦因数μ、因素E—拉拔速度v、因素F—模具直径d这6个因素对拉拔成形复合管残余接触压力p_rc和拉拔力f的影响，选用正交实验法^[21]，取上述6个拉拔参数作为因素，每个因素取5个水平，如表2所列，设计的L₂₅(5⁶)正交表见表3。

表2  正交实验水平因素表

Table 2  Factors and levels of orthogonal experiment

3.2  极差分析

在正交实验的极差分析中，因素的极差值越大反映了其对结果的影响显著性越高。表4所列为正交实验模拟结果的极差分析结果，表中k_i为同一因素下i水平的平均值 (i=1, 2, 3, 4, 5)，?_X为因素X的极差。

根据表4对残余接触压力p_rc的分析结果，可以得到?_F >?_D>?_C>?_A>?_B>?_E。由此说明在6个因素中，模具直径对残余接触压力影响最大，摩擦因数影响其次，定径带长度的影响再次，因此得到在残余接触压力P_rc最大时的最优拉拔工艺参数组合为：F₃D₁C₂A₄B₂E₁；而对拉拔力f的分析，可以得到?_F >?_D>?_A>?_E>?_B>?_C。由此说明在6个因素中，模具直径对拉拔力影响最大，摩擦因数影响其次，模具锥半角影响再次，因此得到在拉拔力f最小时的最优拉拔工艺参数组合为F₁D₁A₅E₃B₂C₂。兼顾各因素对两大分析指标的综合影响，得到拉拔复合管的最优拉拔方案是A₄B₂C₂D₁E₃F₃，即模具锥半角为11?、过渡圆弧半径为3 mm、定径带长度为7 mm、摩擦因数为0.05、拉拔速度为0.03 m/s以及模具直径为17.3 mm。

表3  正交实验方案

Table 3  Scheme of orthogonal experiment

表4  正交实验结果

Table 4  Results of orthogonal experiment

3.3  方差分析

为进一步了解各实验因素对模拟结果影响的量化估计，必须进行方差分析。表5所列为各因素对两大指标影响的方差分析结果，表中“*”表示因素的影响性显著，“#”表示因素对指标有影响，但不显著。分析中F为分布统计量，因素的显著性水平α=0.05。由表中数据知，在对残余接触压力的影响因素中，模具直径的F值大于F的临界值，说明该因素对残余接触压力影响程度较大，其次为摩擦因数的影响，再次为定径带长度的影响，而其它因素由于方差较小，其影响可以忽略；在影响拉拔力的因素中，模具直径的F值大于F的临界值，模具直径的影响还是最为显著，其次摩擦因数的影响，再次为模具锥半角的影响，而其它因素的影响相对较小。极差分析与方差分析的结果表明，在影响残余接触压力及拉拔力的各因素中，模具直径、摩擦因数和模具锥半角的影响较为显著，因此模具直径及模具锥半角的合理设计和对衬管内壁的摩擦有效处理可显著增大残余接触压力及减小拉拔力，从而获得高质量的拉拔复合管及延长模具寿命。

3.4  优化方案的模拟分析

根据正交实验表的安排，得到了一组理论上最优拉拔工艺参数。由于在实验中这组参数没有出现，为了验证正交实验的正确性，对最优的拉拔工艺参数组合进行数值模拟，模拟结果如图9和10所示。从图9可知，拉拔完成后衬管与基管间残余接触压力趋于稳定，平均残余接触压力为19.97 MPa，而从图10可知，稳定拉拔阶段的平均拉拔力为6 566 N，该结果较上述正交实验模拟结果有明显的优化。

3.5  拉拔复合管试验

对优化后的拉拔模具进行拉拔试验，图11所示为硬质合金模具及试验拉管机。在拉拔模具拉拔至报废的情况下，传统的硬质合金模具在该拉管机上拉拔的

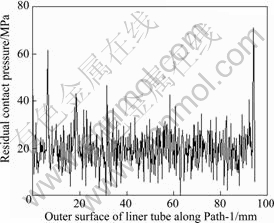
图9  在最优工艺条件下内外管间的残余接触压力模拟曲线

Fig.9  Simulation curve of residual contact pressure of inner and outer pipe under optimized condition

图10  在最优工艺条件下复合管成形过程的拉拔力模拟曲线

Fig.10  Simulation curve of drawing force of composite pipe forming process under optimized condition

表5  模拟结果方差分析

Table 5  Variance analysis of simulation results

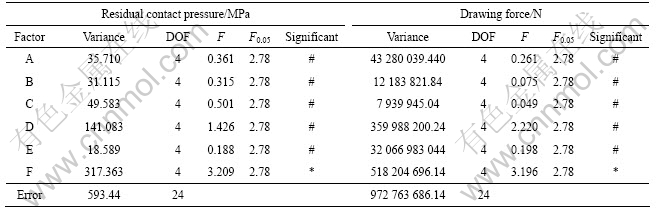
图11  拉拔复合管试验装置

Fig.11  Test equipment of drawing composite pipe

复合管产量约为350 t，而在相同拉拔条件下，优化的硬质合金模具的复合管产量为2 200 t以上，因此，相对于未优化的硬质合金模具，优化的硬质合金模具的寿命可以提高6倍以上。同时，由于对模具的锥角及过渡圆弧进行了优化处理，拉拔后复合管的内表面光洁度也有很大改善，而且也解决了拉拔后的复合管横向及纵向裂纹问题，因此该优化方案可以为复合管拉拔模具的工艺参数选择提供参考。按上述优化工艺生产的内衬316L不锈钢复合管经过技术专家的鉴定满足《内衬不锈钢复合钢管》(CJ/T192—2004)规定，且内外管结合强度远远大于其规定的0.2 MPa，已用在某石化加氢装置高压空冷器上，该空冷器已投产运行18月，未出现腐蚀泄漏问题。

4  结论

1) 通过对内衬316L不锈钢复合管拉拔过程的有限元模拟，分析了稳定拉拔阶段的轴向、径向和环向应力分布，得到了拉拔完成后复合管衬管内壁出现横向裂纹、衬管外壁出现纵向裂纹的原因以及模具与衬管发生剧烈磨损的部位，为控制和提高拉拔复合管的质量提供依据。

2) 根据对残余接触压力及拉拔力分析，拉拔复合管成形过程大致可以分为3个阶段，即初始拉入模具阶段、稳定拉拔阶段和拉出模具阶段，其中稳定拉拔阶段的金属流动趋于稳定，在此阶段可增大拉拔速度，提高复合管的生产效率，拉拔完成后，内外管间残余接触压力趋于稳定，内外管间的残余接触压力远远大于《内衬不锈钢复合钢管》(CJ/T192—2004)规定的要求。

3) 由极差分析可知，当模具锥半角相差不大时，模具直径及摩擦因数都是残余接触压力和拉拔力的主要影响因素，其次是拉拔速度的影响。由方差分析知，模具直径、摩擦因数和模具锥半角的影响较为显著，因此，要获得高质量的拉拔复合管及延长模具寿命，拉拔前对模具及衬管内壁的摩擦处理、模具直径和模具锥半角的合理设计是非常重要的。其次，过渡圆弧半径、拉拔速度、定径带长度的影响也不容忽视。

4) 通过正交实验分析得到在最大残余接触压力及最小拉拔力条件下的最优拉拔工艺参数: 模具锥半角为11?、过渡圆弧半径为3 mm、定径带长度为7 mm、摩擦因数为0.05、拉拔速度为0.03 m/s以及模具直径为17.3 mm。

5) 对优化方案进行数值模拟，拉拔完成后复合管内外管间平均残余接触压力为19.97 MPa，稳定拉拔阶段的平均拉拔力为6 566 N，模拟结果表明了正交实验分析对内衬316L复合管拉拔工艺参数优化的有效性。对参数优化后的模具进行拉拔试验表明，在相同拉拔条件下，相对于未优化的硬质合金模具，优化后的硬质合金模具的工作寿命可以提高6倍以上，而且解决了拉拔后的复合管出现横向及纵向裂纹问题，该工艺拉拔生产的内衬316L不锈钢复合管已成功应用于加氢高压空冷器上。

References

[1] KOBAYASHI S, OH S I, ALTAN T. Metal forming and the finite element method[M]. New York: Oxford University Press, 1989.

[2] 李尚健. 金属塑性成形过程模拟[M]. 北京: 机械工业出版社, 1999: 109-140.
LI Shang-jian. Simulation of metal plastic forming process[M]. Beijing: China Machine Press, 1999: 109-140.

[3] 叶金铎, 温殿英. 空拔管成型过程的非线性有限元分析[J]. 重型机械, 2001(6): 41-44.
YE Jin-duo, WEN Dian-ying. Analysis of the process of the non-mandrel pipe by non-liner finite element[J]. Heavy Machinery, 2001(6): 41-44.

[4] 秦建平, 尹 钢, 李国祯. 双金属管拉拔过程的理论分析[J]. 太原重型机械学院学报, 1993, 14(1): 45-52.
QIN Jian-ping, YIN Gang, LI Guo-zhen. Theoretical analysis for the close-pass drawing of thin-walled Bi-metal tubes[J]. Journal of Taiyuan Heavy Machinery Institute, 1993, 14(1): 45-52.

[5] 秦建平, 尹 钢. 双金属管复合拉拔力计算[J]. 钢管, 1995(1): 22-25.
QIN Jian-ping, YIN Gang. Calculation of complex drawing force for clad steel pipe processing[J]. Steel Pipe, 1995(1): 22-25.

[6] 杨贵平, 王智祥. 双金属管衬拉复合拉拔力的计算[J]. 中国有色金属学报, 1998, 8(3): 447-452.
YANG Gui-ping, WANG Zhi-xiang. Calculation of complex drawing loads for bimetal tube drawing with a fixed plug[J]. The Chinese Journal of Nonferrous Metals, 1998, 8(3): 447-452.

[7] 杨晓静, 孙方宏, 张志明, 沈荷生, 郭松寿. 基于有限元模拟的空拔铜管拉拔参数的优化[J]. 中国有色金属学报, 2008, 18(12): 2245-2252.
YANG Xiao-jing, SUN Fang-hong, ZHANG Zhi-ming, SHEN He-sheng, GUO Song-shou. Optimization of drawing parameters for copper tubes with hollow sinking based on FEM simulation[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(12): 2245-2252.

[8] 薛隆泉, 何亚峰, 刘荣昌, 代春英, 陈军涛. 基于ANSYS/LS-DYNA的空拔钢管有限元分析[J]. 塑性工程学报, 2005, 12(5): 74-77.
XUE Long-quan, HE Ya-feng, LIU Rong-chang, DAI Chun-ying, CHEN Jun-tao. FEA on empty-sunken steel tube based on ANSYS/LSDYNA [J]. Journal of Plasticity Engineering, 2005, 12(5): 74-77.

[9] ALCARAZ J L, GIL-SEVILLANO J. An Analysis of the extrusion of bimetallic tubes by numerical simulation [J]. International Journal of mechanical sciences, 1996, 38(2): 157-173.

[10] BERSKI S, DYJA H, MARANDA A, NOWACZEWSKI J, BANASZEK G. Analysis of quality of bimetallic rod after extrusion process[J]. Journal of Materials Processing Technology, 2006, 177(1/3): 582-586.

[11] 臧新良, 周维海, 杜凤山, 温立刚. 复合管拉拔过程的计算机仿真[J]. 重型机械, 2001(3): 56-57.
ZANG Xin-liang, ZHOU Wei-hai, DU Feng-shan, WEN Li-gang. Computer simulation of clad steel pipe during compound drawing[J]. Heavy Machinery, 2001(3): 56-57.

[12] 杜清松, 曾德智, 杨 斌, 张 智, 黄黎明. 双金属复合管塑性成型有限元模拟[J]. 天然气工业, 2008, 28(9): 64-66.
DU Qing-song, ZENG De-zhi, YANG Bin, ZHANG Zhi, HUANG Li-ming. Finite-element simulation on plastic forming of bi-metal composite pipes[J]. Natural Gas Industry, 2008, 28(9): 64-66.

[13] 杜艳梅, 王开坤, 张 鹏, 马春梅, 徐 锋. 半固态挤压铝/镁合金双金属复合管的有限元模拟[J]. 中国有色金属学报, 2009, 19(2): 208-216.
DU Yan-mei, WANG Kai-kun, ZHANG Peng, MA Chun-mei, XU Feng. FEM simulation on extrusion of double-layer tube of aluminum and magnesium alloys[J].The Chinese Journal of Nonferrous Metals, 2009, 19(2): 208-216.

[14] SCHREYER H L, KULAK R F. Accurate numerical solutions for elastic-plastic models[J]. Journal of Pressure Vessel Technology—Transactions of The ASME, 1979, 101(3): 226-234.

[15] ROBERT H, DODDS J. Numerical techniques for plasticity computation in finite element analysis[J]. Computer & Structures, 1987, 26(4): 267-779.

[16] 刘建生, 陈慧琴, 郭晓霞. 金属塑性加工有限元模拟技术与应用[M]. 北京: 冶金工业出版社, 2003: 38-39.
LIU Jian-sheng, CHEN Hui-qin, GUO Xiao-xia. Finite element simulation and application of metal plastic forming[M]. Beijing: Metallurgical Industry Press, 2003: 38-39.

[17] 徐丙坤, 施法中. 板料冲压成形回弹的数值模拟[J]. 北京航空航天大学学报, 2001, 27(2): 194-197.
XU Bing-kun, SHI Fa-zhong. Numerical simulation of springback in sheet metal forming[J]. Journal of Beijing University of Aeronautics and Astronautics, 2001, 27(2): 194-197.

[18] 赵腾伦. ABAQUS6.6在机械工程中的应用[M]. 北京: 中国水利水电出版社, 2007: 346-351.
ZHAO Teng-lun. The application of ABAQUS6.6 in mechanical engineering[M]. Beijing: Water Publishing Company of China, 2007: 346-351.

[19] 庄 茁, 张 帆, 岑 松. ABAQUS非线性有限元分析与实例[M]. 北京: 科学出版社, 2008.
ZHUANG Zhuo, ZHANG Fan, CEN Song. ABAQUS nonlinear FEM analysis and examples[M]. Beijing: Science Press, 2008.

[20] 苏 岚, 王先进, 唐 荻, 孙吉先, 田荣彬.有限元法处理金属塑性成型过程的接触问题[J]. 塑性工程学报, 2000, 7(4): 12-15.
SU Lan, WANG Xian-jin, TANG Di, SUN Ji-xian, TIAN Rong-bin. A study on contact problem of plastic metal forming with finite element method[J]. Journal of Plasticity Engineering, 2000, 7(4): 12-15.

[21] 方开泰, 马长兴. 正交与均匀设计[M]. 北京:科学出版社, 2001: 35-77.
FANG Kai-tai, MA Chang-xing. Orthogonal and uniform design[M]. Beijing: Science Press, 2001: 35-77.

(编辑 何学锋)

收稿日期：2010-01-21；修订日期：2010-06-01

通信作者：陆晓峰，副教授；电话：025-83712340；E-mail: xflu@njut.edu.cn