J. Cent. South Univ. Technol. (2011) 18: 1525-1531
DOI: 10.1007/s11771-011-0869-1
Online model identification of lithium-ion battery for electric vehicles
HU Xiao-song(胡晓松), SUN Feng-chun(孙逢春), ZOU Yuan(邹渊)
National Engineering Laboratory for Electric Vehicles, Beijing Institute of Technology, Beijing 100081, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: In order to characterize the voltage behavior of a lithium-ion battery for on-board electric vehicle battery management and control applications, a battery model with a moderate complexity was established. The battery open circuit voltage (OCV) as a function of state of charge (SOC) was depicted by the Nernst equation. An equivalent circuit network was adopted to describe the polarization effect of the lithium-ion battery. A linear identifiable formulation of the battery model was derived by discretizing the frequent-domain description of the battery model. The recursive least square algorithm with forgetting was applied to implement the on-line parameter calibration. The validation results show that the on-line calibrated model can accurately predict the dynamic voltage behavior of the lithium-ion battery. The maximum and mean relative errors are 1.666% and 0.01%, respectively, in a hybrid pulse test, while 1.933% and 0.062%, respectively, in a transient power test. The on-line parameter calibration method thereby can ensure that the model possesses an acceptable robustness to varied battery loading profiles.
Key words: battery model; on-line parameter identification; lithium-ion battery; electric vehicle
1 Introduction
Hybrid electric vehicles (HEVs) and battery electric vehicles (BEVs) are being actively developed by automotive companies to reduce the carbon footprint of ground personal transportation [1]. Traction battery pack, a critical sub-system of HEVs/BEVs, is currently the performance bottleneck [2]. Due to the dynamic and complex vehicle operations, a battery management system (BMS) is required to ensure reliable battery operations and a high efficiency of vehicle energy management. The BMS needs to provide accurate knowledge of the state of charge (SOC) of the traction battery pack. Since the SOC of battery cannot be measured directly, it often needs to be estimated by model-based techniques, such as Kalman filters [3-9], and sliding mode observers [10-11]. The performance of these estimation approaches strongly depends on the accuracy of the battery model. Therefore, developing a good battery model is of great significance for the development of HEVs/BEVs.
For on-board battery management and control applications for HEVs/BEVs, a good battery model should be sufficiently simple and can describe the battery behavior with adequate accuracy. Thus, many equivalent circuit-based models [10-14] and simplified electrochemistry-based models [3-5, 8-9, 15-16] were investigated. However, for most above-mentioned equivalent circuit-based battery models, the battery open circuit voltage (OCV) was directly measured or estimated in experiments at several specified SOC values. This method to determine OCV as a function of SOC is time-consuming, laborious and even error-prone. Furthermore, the discrete representation of OCV at several SOC values is not convenient and straightforward for Kalman filtering or observer-based SOC estimation techniques. Although the foregoing simplified electrochemical battery models can use an empirical function to analytically describe the OCV-SOC map, their ability to describe the battery time-constant behavior is often inferior to that of equivalent circuit-based models with resistance-capacitance (RC) networks. On the other hand, the parameters of most of the battery models were identified using batch approaches so that sometimes good model robustness cannot be guaranteed.
In this study, an OCV-SOC map defined by the Nernst equation [17] was incorporated into a first-order RC model so that an explicit OCV-SOC relationship can be achieved in any battery loading profile without doing a special OCV-determination test in advance, and the time-constant behavior of the battery can also be portrayed. A linear identifiable formulation of the proposed model was derived by discretizing the frequent-domain model description. Then, the recursive least square algorithm with forgetting was used to identify the model parameters online. The performance of the modeling algorithm was evaluated over two experimental data sets.
2 Model structure
The battery model structure is shown in Fig.1. Voc denotes OCV which is depicted by the Nernst equation with respect to the SOC of battery, S, where K0 and K1 are two parameters [17]. The RC network (R1, C1) is used to simulate the time-constant behavior of the battery. R2 is the internal ohmic resistance. V is the output voltage of the model. I is the current.
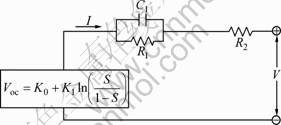
Fig.1 Battery model structure
According to basic electrical principles, the continuous-time frequent-domain form of the battery model can be described as
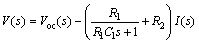 (1)
(1)
The discrete form of Eq.(1) can be achieved by
using the first-order backward difference and substituting
Voc with 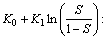
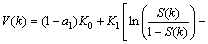
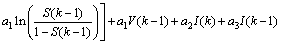
where
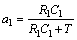 (3)
(3)
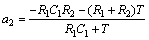 (4)
(4)
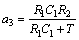 (5)
(5)
k is the time index; T is the sampling time. Since T is small, here S(k) is approximately equal to S(k-1). Thus, Eq.(2) can be reformulated in a linear identifiable fashion:
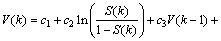
 (6)
(6)
where
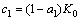 (7)
(7)
 (8)
(8)
c3=a1 (9)
c4=a2 (10)
c5=a3 (11)
After identifying c1, c2, c3, c4 and c5, according to Eqs.(3)-(5) and (7)-(11), the parameters of the battery model can be determined as
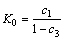 (12)
(12)
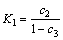 (13)
(13)
 (14)
(14)
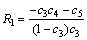 (15)
(15)
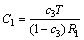 (16)
(16)
3 On-line parameter calibration algorithm for battery model
A forgetting factor can be integrated into the standard recursive least square method such that larger weight will be given to the recent data. Therefore, the linear adaptive filtering with forgetting is quite applicable to on-line parameter calibration for linear time-variant systems [18]. Herein, the recursive least square algorithm with forgetting for Eq.(6) can be illustrated as
 (17)
(17)
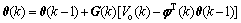 (18)
(18)
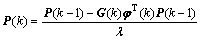 (19)
(19)
where
 (20)
(20)
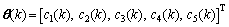 (21)
(21)
Vo denotes the sampled battery voltage and λ (0<λ≤1) is the forgetting factor. According to Eqs.(12)-(16), the five parameters of the model, K0(k), K1(k), R1(k), C1(k) and R2(k) can be attained after identifying the parameter vector θ(k).
The schematic diagram for the on-line parameter calibration of the battery is shown in Fig.2. The initial values of the parameter estimate θ(0) and its error covariance matrix P(0) are firstly provided. Then, the parameter vector θ(k) can be adjusted adaptively according to Eqs.(17)-(19), giving the samples the output voltage, current and SOC of the battery.
4 Experimental results
4.1 Battery test bench
As shown in Fig.3, the battery test bench mainly consists of a digatron battery testing system (BTS-600), a battery management module, a controller area network (CAN) communication unit and a Labview-based virtual measurement unit. The digatron battery testing system is responsible for loading the battery based on the designed program with the maximum voltage of 500 V and the maximum charging/discharging current of 500 A. The recorded quantities include load current, terminal voltage, temperature, accumulative product of current and time (A?h) and product of power and time (W?h). The battery management module can also collect the voltage and temperature of cells within the battery. The errors of the Hall current and voltage sensors are less than 0.2% and 0.5%, respectively. The measured load current is transmitted to the battery management module through CAN bus driven by the Labview program and CAN communication unit. Both the Labview-based measurement unit and the management module have a low-pass filtering function to implement large noise cancellation. The battery SOC can be computed by the digatron battery testing system in a well-controlled condition. The measured voltage, temperature and computed SOC are then transmitted through CAN bus to the Labview for real-time display. A lithium-ion battery module composed of sixteen cells in series was used for experimentation. The actual capacity of the module was 100 A?h.
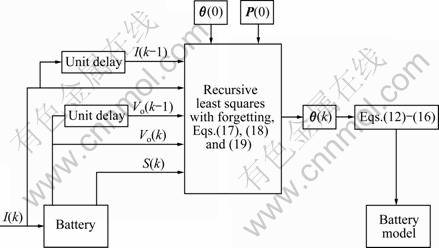
Fig.2 Schematic diagram of battery model identification
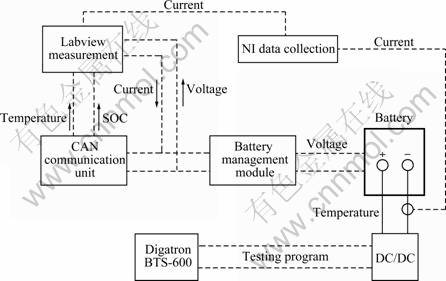
Fig.3 Schematic diagram of battery test bench
4.2 Hybrid pulse test
A hybrid pulse test comprised of a sequence of hybrid pulse power characterization (HPPC) profiles, constant-current discharge pulses and rests was conducted. The sampled voltage, current and SOC for the hybrid pulse test are shown in Fig.4. The sampling time is 1 s. The forgetting factor, λ, for the parameter identification algorithm was set to be 0.999 5 in the hybrid pulse test so as to pursue a good balance between the parameter tacking capability and misadjustment. In other words, the parameters should be adjusted to make the model output error as small as possible, obeying a precondition that the RC parameters are positive. A small θ(0) and a large error covariance matrix P(0) were offered to initialize the identification algorithm. The results of K0, K1 and C1 are shown in Fig.5. Figure 6 shows the results of R1 and R2 after largely reducing the initial parameter errors. It can be seen that the initial errors can be quickly compensated by the proposed algorithm. The voltage prediction φT(k)θ(k) is calculated. The measured and predicted battery voltages and the relative prediction error starting from the first second in the hybrid pulse test are shown in Fig.7. It is obvious that the on-line identified model can accurately describe the dynamical voltage behavior of the lithium-ion battery in the hybrid pulse test. The maximum and mean relative errors are 1.666% and 0.01%, respectively.
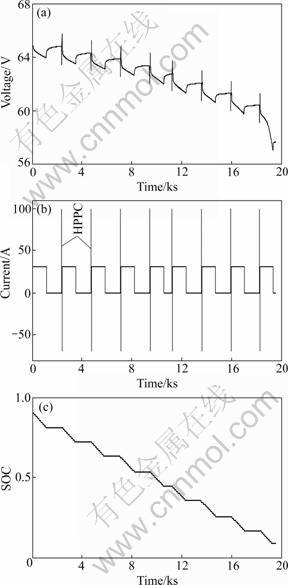
Fig.4 Battery responses in hybrid pulse test: (a) Voltage; (b) Current; (c) SOC
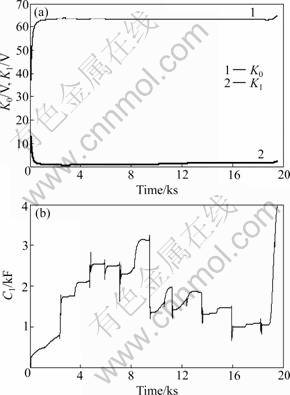
Fig.5 Trajectories of K0, K1 (a) and C1 (b) in hybrid pulse test
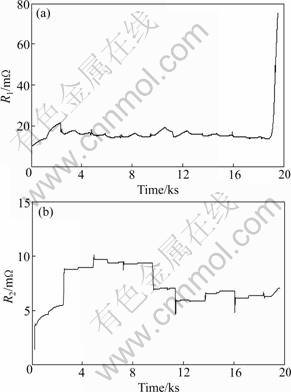
Fig.6 Values of K1 (a) and K2 (b) after largely reducing initial errors in hybrid pulse test
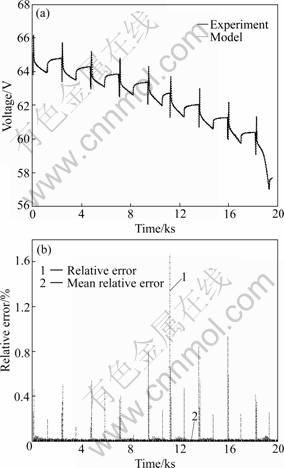
Fig.7 Measured and estimated battery responses (a) and relative estimation error (b) in hybrid pulse test
4.3 Transient battery power test
Another experimental data set collected in a transient power test of the lithium-ion battery was used to further evaluate the modeling validity. The test was comprised of twelve cycles in series. The cycle was a variant of the standard dynamic stress test (DST) cycle, which could be used to simulate the actual driving cycles of electric vehicles. The sampled voltage, current and SOC for the transient power test are shown in Fig.8. It can be seen that the maximum discharging and charging current rates are 5C and 2C, respectively, leading to a dramatic voltage response. These high current rates are closer to the actual battery operations for HEVs/BEVs. Thereby this transient test can better evaluate the performance of the battery model.
The forgetting factor λ was set to be 0.99. The same θ(0) and error covariance matrix P(0) as those in the hybrid pulse test were offered. Figure 9 shows the trajectories of K0 and K1, and the results of C1, R1 and R2 after largely reducing the initial errors. It is clear that the identified parameter trajectories in the transient power test are different from those in the hybrid pulse test. Therefore, there is a great necessity of calibrating the battery parameters on-line. The measured and predicted battery voltages in the transient power test, together with the model relative error, are shown in Fig.10. It is observed that the model can also accurately predict the voltage behavior of the lithium-ion battery in the transient power test. The maximum and mean relative errors are 1.933% and 0.062%, respectively.
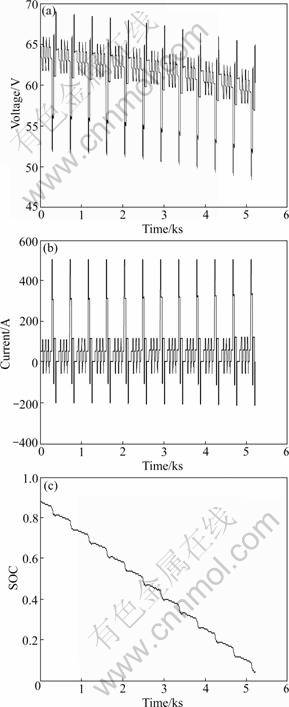
Fig.8 Battery response in transient power test: (a) Voltage; (b) Current; (c) SOC
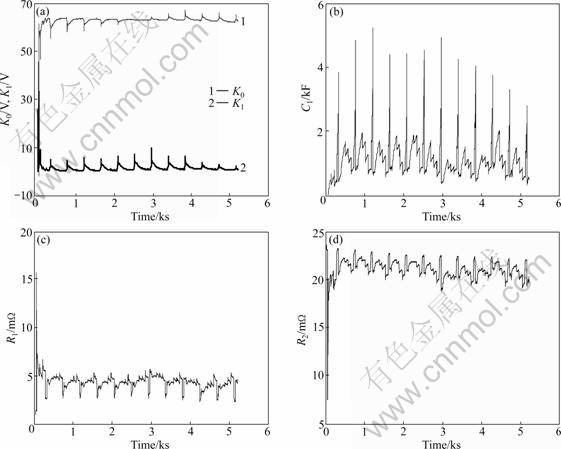
Fig.9 Results of battery parameterization in transient power test: (a) Trajectories of K0, K1; (b) C1; (c) R1; (d) R2
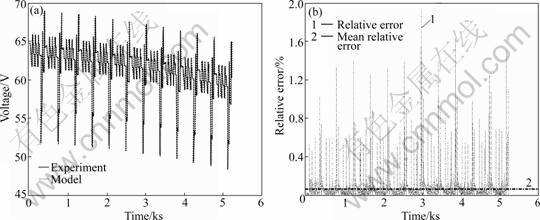
Fig.10 Measured and estimated battery responses (a) and relative estimation error (b) in transient power test
5 Conclusions
1) An OCV-SOC map analytically defined by the Nernst equation is incorporated into a first-order equivalent circuit RC model structure so that an arduous and error-prone experiment for specially determining OCV is not required, and the time-constant behavior of the battery can be depicted effectively. The model structure can facilitate Kalman filtering or observer- based SOC estimation.
2) A linear discrete-time identifiable form of the model is derived from the frequent-domain representation of the battery model.
3) The recursive least square algorithm with forgetting is applied to implement on-line parameter calibration on the basis of the linear identifiable form.
4) The experimental results show that the model has a good performance in predicting the voltage behavior of the lithium-ion battery. The maximum and mean relative errors are 1.666% and 0.01% in a hybrid pulse test, while they are 1.933% and 0.062% in a transient power test. Hence, an acceptable robustness of the model to varying battery loading profiles can be obtained. The on-line battery parameterization approach is much significant for the development of HEVs/BEVs.
Acknowledgements
The authors would like to express deep gratitude to Professor Huei Peng in University of Michigan in USA for many helpful suggestions.
References
[1] JOHANSSON B, M?RTENSSON A. Energy and environmental costs for electric vehicles using CO2-neutral electricity in Sweden [J]. Energy, 2000, 25(8): 777-792.
[2] ?HMAN M. Primary energy efficiency of alternative powertrains in vehicles [J]. Energy, 2001, 26(11): 973-989.
[3] PLETT G L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 1. Background [J]. Journal of Power Sources, 2004, 134(2): 252-261.
[4] PLETT G L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2. Modeling and identification [J]. Journal of Power Sources, 2004, 134(2): 262-276.
[5] PLETT G L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation [J]. Journal of Power Sources, 2004, 134(2): 277-292.
[6] PLETT G L. Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 1. Introduction and state estimation [J]. Journal of Power Sources, 2006, 161(2): 1356-1368.
[7] PLETT G L. Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2. Simultaneous state and parameter estimation [J]. Journal of Power Sources, 2006, 161(2): 1369-1384.
[8] HAN J Y, KIM D C, SUNWOO M. State-of-charge estimation of lead-acid batteries using an adaptive extended Kalman filter [J]. Journal of Power Sources, 2009, 188(2): 606-612.
[9] WANG Jun-ping, GUO Jing-gang, DING Lei. An adaptive Kalman filtering based State of Charge combined estimator for electric vehicle battery pack [J]. Energy Conversion and Management, 2009, 50(12): 3182-3186.
[10] KIM I S. The novel State of Charge estimation method for lithium battery using sliding mode observer [J]. Journal of Power Sources, 2006, 163(1): 584-590.
[11] KIM I S. Nonlinear state of charge estimator for hybrid electric vehicle battery [J]. IEEE Transactions on Power Electronics, 2008, 23(4): 2027-2034.
[12] LIN Cheng-tao, QIU Bin, CHEN Quan-shi. Comparison of current input equivalent circuit models of electric vehicle battery [J]. Chinese Journal of Mechanical Engineering, 2005, 41(12): 76-81. (in Chinese)
[13] DAI Hai-feng, WEI Xue-zhe, SUN Ze-chang. Estimate State of Charge of power lithium-ion batteries used on fuel cell hybrid vehicle with method based on extended Kalman filtering [J]. Chinese Journal of Mechanical Engineering, 2007, 43(2): 92-95. (in Chinese)
[14] LI Chao. Research on model identification and SOC estimation for EV NiMH battery [D]. Tianjin: Tianjin University, 2007. (in Chinese)
[15] WANG Jun-ping, CAO Bing-gang, CHEN Quan-shi, WANG Feng. Combined state of charge estimator for electric vehicle battery pack [J]. Control Engineering Practice, 2007, 15(12): 1569-1576.
[16] WANG Jun-ping, CAO Bing-gang, CHEN Quan-shi. Self-adaptive filtering based State of Charge estimation method for electric vehicle batteries [J]. Chinese Journal of Mechanical Engineering, 2008, 44(5): 76-79. (in Chinese)
[17] OTA Y, SAKAMOTO M, KIRIAKE R, KOBE T, HASHIMOTO Y. Modeling of voltage hysteresis and relaxation of HEV NiMH battery [C]// Proceedings of the 17th IFAC World Congress. New York: IFAC, 2008: 4654-4658.
[18] HAYKIN S. Adaptive Filter Theory [M]. 3rd edition. New Jersey: Prentice Hall, 1996: 562-587.
(Edited by YANG Bing)
Foundation item: Project(50905015) supported by the National Natural Science Foundation of China
Received date: 2010-09-09; Accepted date: 2011-03-18
Corresponding author: ZOU Yuan, Associate Professor, PhD; Tel: +86-10-68915205; E-mail: zouyuan05@gmail.com