Article ID: 1003-6326(2005)02-0319-04
Size dependent phase stability of nano-diamond
JIANG Qing(蒋 青), LU Hai-ming(陆海鸣), ZHENG Wei-Tao(郑伟涛)
(State Key Laboratory of Automobile Materials, Department of Materials Science and Engineering,
Jilin University, Changchun 130025, China)
Abstract: The transition between nano-diamond(n-D) and nano-graphite(n-G) were modeled based on the extrapolation of the bulk diamond-graphite equilibrium phase boundary in the temperature-pressure diagram to the nano-size region. It is found that in comparison with n-G, the stability of n-D increases as size and temperature decrease. However, n-D is not the most stable phase in comparison with fullerenes(C60) at the nanoscale by considering the heat of formation.
Key words: solid-solid transition; graphite; diamond; fullerenes CLC number: O0414.12
Document code: A
1 INTRODUCTION
Recently, n-D powder has become a useful engineering material in many fields for its technically important properties, i.e., high hardness, strength, electrical resistivity and magnetoresistivity as well as special optical properties. However, it has been observed that n-D can be obtained at low temperature and pressure although it is well known that the graphite-to-diamond transition occurs at high temperature and pressure[1]. Moreover, n-D that initially formed with grain size (d) below 3nm transforms into graphite at a larger size[1]. Nuth[2] proposed that n-D could be stable than graphite due to the larger product of surface area and surface energy, and Hwang et al[3, 4] outlined a chemical potential model and a charged cluster model to describe the relative stability of small diamond and graphite clusters in their study of low pressure diamond synthesis. All of the above-mentioned methods predict that n-D is the stable phase of carbon at d less than 6.0nm. On the other hand, it has been reported that carbon nanoparticles undergo n-D, bucky diamond, carbon onion and fullerence with the reduction of size where n-D will disappear at d〈2.0nm[5]. Moreover, the phase transition of n-D to carbon onions has been observed experimentally with a transformation temperature that is dependent on the size of the particle[6, 7]. If these transformations happen, n-D cannot stably exist. Thus, the stability of n-D is necessary to be considered further.
In this contribution, the stability of n-D is thermodynamically considered in terms of the extrapolation of the bulk diamond-graphite equilibrium phase boundary in the temperature-pressure diagram to the nano-size region and the comparison of the formation heats between n-D and C60.
2 MODEL
According to the phase diagram of carbon[1], the transition pressure function p(T) for the diamond-graphite transition is given as[8, 9]
p(T)=1700+2.06T(1)
Eqn.(1) is determined by the two linearly connected terminating points of the graphite-diamond phase boundary in the phase diagram of carbon that are (1700MPa, 0K) and (12000MPa, 5000K)[1], respectively, the latter is the graphite/diamond/liquid triple point[1]. Thus, dp/dT=(12000-1700)/5000=2.06. Eqn.(1) is established by thermodynamic calculations in terms of the measured physical properties of graphite and diamond in the temperature range between 300 and 1200K, and by experiments on the graphitization of diamond[1].
In order to estimate the contribution of the size-dependent internal pressure, some assumptions have to be made. Under the assumption of spherical, for quasi-isotropic nanocrystals with a diameter d, the additional curvature-induced internal pressure pi is given by the Laplace-Young equation as[8, 9]
pi=4f/d(2)
where f is the surface stress.
Owing to this additional internal pressure pi, the external pressure po necessary for the transition between n-G and n-D decreases by the same amount. Thus, pi+po=1700+2.06T is obtained for the size dependent phase boundary. In terms of this expression and considering that during the low-temperature and low-pressure synthesis of diamond, the external pressure can be ignored[3], i.e. p≈pi. Considering these expressions, there is
d=4f/(1700+2.06T)(3)
The value of f value of a quasi-isotropic nanocrystal can be determined by[8, 9]
f =(3Bd0γsl/8)1/2(4)
where γsl is the bulk solid-liquid interface energy and B is the bulk modulus. d0 is the critical particle diameter where almost all atoms are located on its surface, which equals 3h for a particle or a wire having a curved surface and 2h for any kind of low-dimensional crystals with a plane surface (h is the atomic diameter)[8, 9], respectively.
In Eqn.(4), γsl has been deduced according to the Gibbs-Thomson equation[8],
γsl=2hSvibHm(T)/(3VR)(5)
where R is the ideal gas constant, Hm(T) is the temperature-dependent melting enthalpy, Svib is the vibrational part of the overall melting entropy Sm, V is the gram atom volume. Since T concerned here is far lower than the ideal glass transition temperature Tk and Tk=Tm/2 for diamond and graphite, Hm(T)=Hm(Tk)=Hm/4 is taken in terms of Helmholtz function[8]. Now, γsl for graphite and diamond can be rewritten as
γsl=hSvibHm/(6VR)(6)
Since carbon nanoparticles undergo n-D, bucky diamond, carbon onion and fullerence (C60) with the reduction of size[5], strictly speaking, the lower limit of phase stability of n-D should be determined compared with bucky diamond (even carbon onion) rather than fullerenes. However, the most of thermodynamic parameters of bucky diamond and carbon onion are unavailable, which makes that fullerenes are used for comparison although this treatment will result in some deviations. However, the temperature-pressure equilibrium phase diagram between diamond and fullerences does not exist, the above-mentioned way does not work. To estimate the relative phase stability of n-D and C60, the size-dependent formation heat ΔHf(d) is considered, which can be expressed as a function of surface energy γsv, surface area A, cohesive energy Ecoh, curvature-induced strain energy Estrain=pV=4fV/d. With A=6V/d for spherical particles, ΔHf(d) of n-D or C60 can be written as
ΔHf(d)=Ecoh+6γsvV/d+4fV/d(7)
3 RESULTS AND DISCUSSION
At equilibrium, n-D and n-G should have the same p and f, to avoid the difference between fD and fG in terms of Eqn.(4), as a first order approximation, f=(fD+fG)/2 is taken. Moreover, Svib≈0.19Sm for three phases is estimated as a mean value of Si and Ge since they belong to the same IVA group (Svib≈0.22Sm for Si and Svib≈0.15Sm for Ge)[9]. The prediction in terms of Eqn.(3) is shown in Fig.1 with the needed parameters in Table 1[10-16]. For comparison, some theoretical and experimental results[8, 9] are also shown. As d and T decrease, the stability of n-D in comparison with n-G increases, and the critical sizes of n-D decrease from about 8.2nm at 0 K to 3nm at 1400K, which is in agreement with the experimental and theoretical results. According to the Clausius-Clapeyron equation[8],
ΔH=(dp/dT)(VG-VD)T(8)
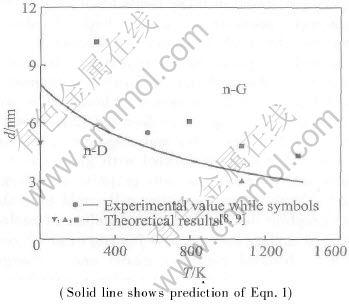
Fig.1 Size—temperature transition diagram of carbon at zero pressure
where ΔH is the transition enthalpy between graphite and diamond, J/mol. Note that dp/dT=2.06J/(cm3·K), thus
ΔH=3.87T(9)
and
ΔS=ΔH/T=3.87(10)
where ΔS is the corresponding transition entropy, J/(mol·K). This value corresponds to ΔS=3.37J/(mol·K) at room temperature and ΔS=4.59J/(mol·K) at 1073-1373K used by Gamamik[17], which contributes partly to the decrease of equilibrium size of the diamond-graphite transition. The mean value of the ΔS is 3.98J/(mol·K), which is very close to our result. Note that Eqn.(9) implies ΔH(T=0)=0, which disagrees with the experimental results of ΔH(T=0)=2.42kJ/mol[18]. Thus, the above results are reasonable only when T>TD where TD is Debye temperature, or above room temperatures. However, Eqn.(9) indicates indeed that as T increases, specific heat difference of the two phases Δcp leads to a linear increase of ΔH, or Δcp is temperature independent at T>TD.
Since C60 structure can be considered finite two-dimensional analogues of graphite, the values of h and Hm are assumed to be the same as those of graphite. Since n-D and C60 concerned here are nanoparticles, thus d0=3h. Moreover, n-D is usually transformed into C60 by annealing n-D at about T=2000K[19], which is larger than Tm of C60, thus Hm(T)=Hm in Eqn.(5), and γsl for C60 is expressed as
γsl=2hSvibHm/(3VR)(11)
In terms of Eqn.(7) with the necessary parameters listed in Table 1, the formation heats ΔHf of n-D and C60 are calculated and shown in Fig.2. It is known that the phase with smaller ΔHf will be more stable than one with larger ΔHf. Thus, it is obvious in Fig.2 that n-D is not the most stable phase of carbon nanoparticles when the size of particle is lower than 2.1nm, which is consistent with other theoretical result[5, 10]. Although the lower limit of stability of n-D is made through the comparison of the formation heats between n-D and C60 rather than between n-D and bucky diamond or carbon onions, the deviation is very small. The reason may be the smaller energetic differences among bucky diamond, carbon onions and C60 (as shown in Figs.2 and 3 in Ref.[5]) and the same sp2-bonding except that the core of bucky diamond is sp3-bonding.
Table 1 Thermodynamic parameters of graphite(G), diamond(D) and C60
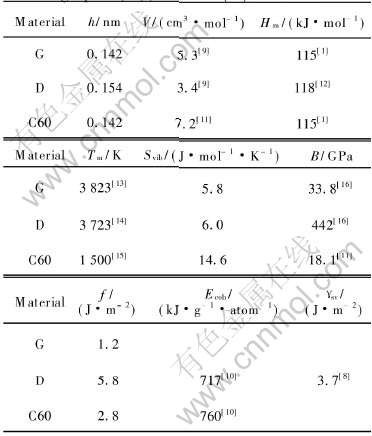
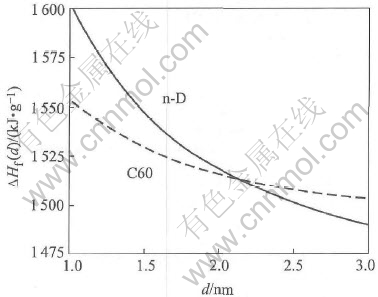
Fig.2 Calculated formation heat(ΔHf) as function of particle diameter (d) for
n-D(solid line) and C60 (three-point-segment line) in terms of Eqn.(4)
4 CONCLUSIONS
Based on the temperature-pressure phase diagram of carbon and considerations of heat of formation of n-D and C60, the stability of n-D is thermodynamically are determined. It is found that as d and T decrease, the stability of n-D in comparison with n-G increases. However, when d〈2.1nm, C60 is more stable than n-D.
REFERENCES
[1]Bundy F P, Bassett W A, Weathers M S, et al. The pressure-temperature phase and transformation diagram for carbon; Update through 1994 [J]. Carbon, 1996, 34(2): 141-153.
[2]Nuth J A. Small-particle physics and interstellar diamonds [J]. Nature, 1987, 329(3): 589-589.
[3]Hwang N M, Hahn J H, Yoon D Y. Chemical potential of carbon in the low pressure synthesis of diamond [J]. J Cryst Growth, 1996, 160(1-2): 87-97.
[4]Hwang N M, Hahn J H, Yoon D Y. Charged cluster model in the low pressure synthesis of diamond [J]. J Cryst Growth, 1996, 162(1-2): 55-68.
[5]Barnard A S, Russo S P, Snook I K. Coexistence of bucky diamond with nanodiamond and fullerene carbon phases [J]. Phys Rev B, 2003, 68(7): 073406-9.
[6]Kuznetsov V L, Zilberberg I L, Butenko Yu V, et al. Theoretical study of the formation of closed curved graphite-like structures during annealing of diamond surface [J]. J Appl Phys, 1999, 86(2): 863-870.
[7]Tomita S, Sakurai T, Ohta H, et al. Structure and electronic properties of carbon onions [J]. J Chem Phys, 2001, 114(17): 7477-7482.
[8]Jiang Q, Li J C, Wilde G. The size dependence of the diamond-graphite transition [J]. J Phys Condens Matter, 2000, 12(26): 5623-5627.
[9]Zhao D S, Zhao M, Jiang Q. Size and temperature dependence of nanodiamond-nanographite transition related with surface stress [J]. Diam Relat Mater, 2002, 11(2): 234-236.
[10]Barnard A S, Russo S P, Snook I K. Size dependent phase stability of carbon nanoparticles: Nanodiamond versus fullerenes [J]. J Chem Phys, 2003, 118(11): 5094-5097.
[11]Sundqvist B. Fullerenes under high pressures [J]. Advances in Physics, 1999, 48(1): 1-134.
[12]Viecelli J A, Bastea S, Glosli J N, Ree F H. Phase transformations of nanometer size carbon particles in shocked hydrocarbons and explosives [J]. J Chem Phys, 2001, 115(6): 2730-2736.
[13]Kim S G, Tománek D. Melting the fullerences: A molecular dynamics study [J]. Phys Rev Lett, 1994, 72(15): 2418-2421.
[14]Dean J A. Langes Handbook of Chemistry [M]. Beijing: Beijing World Publishing Corporation and Mcgraw-Hill Book Companies, 1999. 285.
[15]Zubov V I, Tretiakov N P, Sanchez J F, et al. Thermodynamic properties of the C60 fullerite at high temperatures: Calculations taking into account the intramolecular degrees of freedom and strong anharmonicity of the lattice vibrations [J]. Phys Rev B, 1996, 53(18): 12080-12085.
[16]Hanfland M, Beister H, Syassen K. Graphite under pressure: Equation of state and first-order Raman modes [J]. Phys Rev B, 1989, 39(17): 12598-12603.
[17]Gamamik M Y. Size-related stabilization of diamond nanoparticles [J]. Nanostruct Mater, 1996, 7(6): 651-658.
[18]Weast R C. CRC Handbook of Chemistry and Physics [M]. 69th ed. Cleveland: Chemical Rubber Co, 1988-1989. D58.
[19]Tometa S, Burian A, Dore J C, et al. Diamond nanoparticles to carbon onions transformation: X-ray diffraction studies [J]. Carbon, 2002, 40(9): 1469-1474.
Foundation item: Project(2004CB619301) supported by the National Basic Research and Development Program; Project(50025101) supported by the National Natural Science Foundation of China
Received date: 2004-11-22; Accepted date: 2005-01-18
Correspondence: JIANG Qing, Professor, PhD; Tel: +86-431-5095371; E-mail: jiangq@jlu.edu.cn
(Edited by LONG Huai-zhong)