一种基于Alopex和分布估计算法融合的进化算法
及其在参数估计中的应用
李飞1, 2,李绍军1,梅真贞1
(1. 华东理工大学 化工过程先进控制和优化技术教育部重点实验室,上海,200237;
2. 中广核工程有限公司 设备采购与成套中心,广东 深圳,518124)
摘要:构造了一种基于Alopex(Algorithm of pattern extraction)和分布估计算法(Estimation of distribution algorithm, EDA)相融合的进化算法EDA-Alopex。该算法将分布估计算法嵌入到一种基于Alopex的群智能进化算法(Alopex-based evolutionary algorithm, AEA)中,利用分布估计算法收敛速度快及与传统进化算法进化模式不同的特点来改进AEA算法。新算法综合了AEA算法搜索得到的个体间相关性信息和EDA搜索过程中得到的全局概率信息,能够更好地指导种群向有利的区域进化。仿真结果表明:EDA改进的EDA-Alopex算法搜索性能与AEA算法的搜索性能相比有较大提高,特别是其收敛速度与AEA算法相比有明显提高。
关键词:Alopex;分布估计算法;函数优化;参数估计
中图分类号:TP311 文献标志码:A 文章编号:1672-7207(2011)07-1973-08
A new evolutionary algorithm combining Alopex with estimation of distribution algorithm and its application to parameter estimation
LI Fei1, 2, LI Shao-jun1, MEI Zhen-zhen1
(1. Key Laboratory of Advanced Control and Optimization for Chemical Processes, Ministry of Education,
East China University of Science and Technology, Shanghai 200237, China;
2. Equipment Procurement and Supply Center, China Nuclear Power Engineering Co. Ltd., Shenzhen 518124, China)
Abstract: A new evolutionary optimization algorithm (EDA-Alopex) based on Alopex and estimation of distribution algorithm (EDA) was constructed. In EDA-Alopex, EDA was embedded into Alopex-based evolutionary algorithm (AEA) for the purpose of improving the performance of AEA, owing to a fast convergence and unique evolutionary model owned by EDA. The proposed algorithm integrated the correlation information between different individuals obtained by AEA algorithm with the global probability information extracted by EDA, which can guide the population to evolve toward more promising domain. The results show that the search performance of EDA-Alopex improved by EDA gains a relatively great improvement, particularly its convergence speed has obvious advantages compared with the single AEA algorithm.
Key words: Alopex; estimation of distribution algorithm (EDA); function optimization; parameter estimation
Alopex[1-3](Algorithm of pattern extraction)算法首先于1974年被提出,用于确定视觉感受野形状,后来用来解决一些组合优化和模式匹配问题。该算法具有较强的局部精细搜索能力和较高的精度。将自变量的变化对函数值的影响作为启发信息,同时,利用迭代中的过程参数引入了概率,使算法具有一定的爬坡能力,是一种启发式和随机优化相结合的算法。受到Alopex思想的启发,李绍军[4]提出一种基于Alopex的群智能进化算法(Alopex-based evolutionary algorithm, AEA)。该算法将Alopex算法的启发方式和群体进化相结合,同时改进了原始Alopex算法的退火方式,取而代之的是一种自适应的退火策略,退火的初始温度无需给定,而是根据种群的搜索状况自动调节,提高了算法的搜索效率。该算法每次迭代要产生2个种群进行个体之间的相关性计算,以此作为启发信息来产生新的个体,这2个种群包含的搜索信息在很大程度上决定了算法的收敛速度和获得的最优解的质量。分布估计算法[5-6]于1996年被提出,其实质是扩展的遗传算法和概率统计的结合[7]。由于其具有独特的进化方式,逐渐成为进化计算领域研究的热点。分布估计算法中,没有传统进化算法中对种群个体的操作,而是通过采样概率模型来产生下一代种群。分布估计算法利用的是全局概率信息,通过概率模型来描述种群的进化趋势,从宏观的角度来引导种群进化。分布估计算法有着与传统的进化算法截然不同的进化方式,将传统的进化算法和分布估计算法相结合,种群可以获得更多的进化信息。张智晟等[8]将分布估计算法和遗传算法结合,应用于神经网络故障诊断模型,克服了神经网络训练容易陷入局部最优的缺点,提高了网络的泛化能力。Sun等[9]将分布估计算法和差分进化算法融合,利用EDA改进的差分算法在收敛性能和获得的解的质量方面均有较大提高。EDA与AEA的进化方法不同,EDA不对个体进行遗传、变异、差分之类的操作,而是通过估计优良个体集的统计参数,建立描述整个种群进化趋势的概率模型,是一种从宏观层面引导种群进化的算法[8]。AEA是一种基于Alopex的进化算法,它的操作都是针对种群中每一个个体进行的,在每次迭代中所有变量同时行走一定的步长,然后,评价自变量变化对目标函数值的影响,所以,是一种微观层面的进化。为了进一步改善AEA算法的性能,增加种群的多样性,以获得更多的进化信息,本文作者将变量无关的分布估计算法(UMDAc)引入到AEA算法形成一种混合优化算法EDA-Alopex。在EDA-Alopex中,利用EDA来产生AEA算法执行所需的2个种群,然后执行Alopex操作。这样,种群不仅包含了Alopex的启发信息,同时包含了EDA获得的全局概率进化信息。最终,给出一种概率分布和相关性启发相结合的优化算法。
1 基于Alopex的进化算法(AEA)和分布估计算法(EDA)
AEA采用Alopex的计算方法来实现群体进化,每次迭代,所有个体同时更新,并且利用过程参数实现了温度的自调整。假设有2个种群X1和X2,种群规模均为L,自变量维数为N,从种群X1和种群X2分别随机选取1个个体,分别代表时刻(t-1)和(t-2) 2个状态向量,计算2个向量差?x和对应的函数值差?F的乘积?x??F,然后,通过计算概率p来确定种群X1中个体每一维变量向前或者向后的行走方向,从而使种群X1中个体的每一维变量向能使函数值减小的方向行走。将种群X1中个体的每一维变量增加或者减小一定步长得到新个体,进而构成中间种群 ,将中间种群
,将中间种群 中个体目标函数值和种群X1中对应个体的函数值进行比较,若获得改进,则替换种群X1中原有个体,否则,保留X1中个体,由此得到下一代种群。算法第k次迭代的计算公式如下[4]:
中个体目标函数值和种群X1中对应个体的函数值进行比较,若获得改进,则替换种群X1中原有个体,否则,保留X1中个体,由此得到下一代种群。算法第k次迭代的计算公式如下[4]:

 (1)
(1)
 (2)
(2)
 (3)
(3)
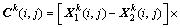
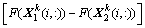 (4)
(4)
 (5)
(5)
式中: 表示第k次迭代种群X1中第i个个体的第j维变量;
表示第k次迭代种群X1中第i个个体的第j维变量; 为得到的中间种群
为得到的中间种群 中第i个个体的第j维变量;rand(0,1)为0到1之间服从均匀分布的随机数;
中第i个个体的第j维变量;rand(0,1)为0到1之间服从均匀分布的随机数; 为第i个个体的第j维变量的行走方向;
为第i个个体的第j维变量的行走方向;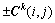 中正负号的选取视函数的优化目的而定,求取函数的最大值时,取负号,求取最小值时取正号;
中正负号的选取视函数的优化目的而定,求取函数的最大值时,取负号,求取最小值时取正号; 表示种群X1中第i个个体对应的函数值;
表示种群X1中第i个个体对应的函数值; 为第k次迭代的退火温度。
为第k次迭代的退火温度。
连续域变量无关的分布估计算法UMDAc (Univariate marginal distribution algorithm for continuous domains)不考虑变量之间的相关性,因此,对于n个相互独立且服从正态分布的变量,它们的联合概率密度为n个独立变量的边缘概率密度的乘 积[9-10]。在UMDAc中,N维独立变量第k代的联合概率密度为:
 (6)
(6)
其中:
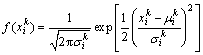 (7)
(7)
在算法每次迭代中,对于每一维变量,有2个参数需要确定:平均值 和标准差
和标准差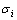 ,第k次迭代对这2个参数的估计公式如下:
,第k次迭代对这2个参数的估计公式如下:
 (8)
(8)
 (9)
(9)
其中:M为算法在第k次迭代选择得到的优良个体数目;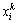 为第k次迭代第i维变量值。
为第k次迭代第i维变量值。
本文中,优秀个体的选择采用截断选择(Truncation selection)[11]。在截断选择中,将种群个体根据目标函数值进行排序,依照函数优化的目的不同,只有一定数目的函数值最大或者最小的个体才作为优良个体被选择,当求函数的最大值时,选取一定数目的函数值较大的个体,当求取函数的最小值时,选取函数值较小的个体。这里,被选择的优良个体数目和整个种群中个体的数量(即种群大小)的比值定义为优良个体选择率w,采样得到的新个体替换原有个体的比例定义为种群更新率v。
2 基于Alopex和EDA融合的新算法EDA-Alopex
将EDA和AEA进行融合。由于这2种算法的进化方式完全不同,融合的算法更能发挥二者的优势,综合EDA算法收敛速度快、AEA算法局部搜索能力强和搜索精度高的优点。在EDA-Alopex中,AEA算法执行所需的2个种群X1和X2由EDA来生成,然后,传递给AEA算法执行Alopex操作。这样种群实质上是以2种方式进化,既使用Alopex的启发方式,又有EDA的进化策略,所以,除了原来AEA获得的个体间自变量的相对大小对函数值影响的一种类似梯度的搜索信息,种群还包含了全局的概率信息,更有利于指导种群的进化。由于变量无关的分布估计算法执行非常简单,所以,在不显著增加AEA算法执行时间的前提下,嵌入EDA的AEA算法与单一的AEA算法相比可以获得更好的解,特别是在收敛速度和算法的效率方面,得到明显的提高。EDA-Alopex的计算步骤如下(以函数F(x1, x2, …, xN)求最小值为例进行说明)。
Step 1 初始化EDA-Alopex算法的参数。设定算法的最大迭代次数或者目标函数的寻优目标值,种群规模优良个体选择率w和种群更新率v,在可行域内初始化种群,计算种群中每个个体对应的目标函数值,设当前迭代次数为k =0。
Step 2 根据当前种群目标函数值从小到大排序,采用截断选择的方法,根据预先给定的优良个体选择率w,建立优良个体集Q。
Step 3 基于优良个体集Q,根据式(8)和(9)计算每一维变量的平均值 和标准差
和标准差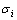 (i=1, 2, …, N),由此建立如式(6)和(7)描述的概率模型。
(i=1, 2, …, N),由此建立如式(6)和(7)描述的概率模型。
Step 4 采样服从正态分布的概率模型得到新种群,即利用式(6)和(7)描述的正态分布产生一个新种群,种群中的每一维变量服从正态分布。判断新种群中个体的每一维变量是否超出可行域,对超出可行域的变量进行修正,然后,将采样得到的新种群按照种群更新比例v更新原有种群,得到种群X1。
Step 5 重新排列种群X1中个体顺序(个体排列次序顺序后移)得到第2个种群X2。根据式(3)计算种群中不同个体之间相关性C,然后,根据相关变量C及退火温度T得到概率p。
Step 6 更新种群X1中个体。根据式(1)更新种群X1得到一个中间种群 。种群
。种群 中个体的函数值F(
中个体的函数值F( )和种群X1中对应个体的函数值F(X1)进行比 较,二者中函数值较小的个体被保留,作为下一代种群个体。
)和种群X1中对应个体的函数值F(X1)进行比 较,二者中函数值较小的个体被保留,作为下一代种群个体。
Step 7 判断是否满足算法的终止条件。若不满足,则令k=k+1,返回step 2。
Step 8 输出最优值及最优个体。
由于种群更新率 的存在,在每一次迭代中,由概率模型采样得到的新种群并不是完全更新原有的种群,而是根据给定的种群更新率进行部分更新,所以,上一代的部分优秀个体得到保留,算法内在的流程包含精英个体保留机制。分析算法的流程可得:从初始种群开始,在种群更新率v<1的情况下,种群部分更新,所以,种群一部分个体始终是以AEA算法的Alopex方式在进化,种群另一部分个体是以EDA-Alopex的方式在进化,在种群规模较大的情况下,保证了EDA-Alopex算法无论在获得的解的质量方面还是收敛速度方面均优于单一的AEA算法。
的存在,在每一次迭代中,由概率模型采样得到的新种群并不是完全更新原有的种群,而是根据给定的种群更新率进行部分更新,所以,上一代的部分优秀个体得到保留,算法内在的流程包含精英个体保留机制。分析算法的流程可得:从初始种群开始,在种群更新率v<1的情况下,种群部分更新,所以,种群一部分个体始终是以AEA算法的Alopex方式在进化,种群另一部分个体是以EDA-Alopex的方式在进化,在种群规模较大的情况下,保证了EDA-Alopex算法无论在获得的解的质量方面还是收敛速度方面均优于单一的AEA算法。
3 算法性能测试
为了检验EDA-Alopex算法的优化性能,将EDA-Alopex与EDA和AEA通过10个常用的典型测试函数[12-13]从不同角度进行了测试对比,这些函数既有单峰的,也有多峰的,每一个函数都有不同的特点,可以综合考查算法的性能。10个测试函数的全局最小值均为0,对于寻优难度较大的函数定为10维,容易的函数定为30维。对于所有的算法,种群大小定为100,算法初始种群都是随机散布在解空间。算法EDA-Alopex经过反复试验,确定优良个体选择率w为0.5,种群更新率v为0.9。测试函数如表1所示。
EDA-Alopex,EDA和AEA算法在每个测试函数上单独连续运行50次,每次迭代1 000代,最大函数评价次数为100 000次。3种算法源代码均以MATLAB编写。对于EDA算法,优良个体同样选择率w定为0.5,种群更新率v为0.9。表2统计了每种算法对每个测试函数在50次运行中得到的平均最优值和标准差,用这2个统计量来表征算法的搜索精度和寻优稳定性。同时,EDA-Alopex所获得的解优于其他2种算法的由黑体标出。各个测试函数的优化结果如表2所示。
由表2可以看出:在10个测试函数中,EDA- Alopex获得的解其中有7个测试函数得到的结果优于其他2种算法获得的结果。在算法的寻优稳定性方面,EDA-Alopex算法中8个测试函数得到的标准差比其他2种算法的小,表明该算法具有更稳定的寻优能力。为了测试算法的收敛速度和效率,对该算法从另外一个角度进行测试,先设定算法的最大迭代次数和目标函数的精度。若算法在最大迭代次数之内达到设定的精度,则认为当次搜索成功,停止迭代,记录迭代次数,否则认为这次搜索失败。每种算法连续反复运行100次,共对4个参数进行统计:100次单独计算中搜索成功的次数R,平均迭代次数G,迭代次数标准差DS以及平均函数调用次数F。算法的最大迭代次数分别设为1 000,2 000和3 000,目标函数对应的精度分别为0.1,0.01和0.001,统计结果如表3~5所示。
表1 测试函数
Table 1 Test functions

表2 1 000次迭代后的优化结果对比
Table 2 Comparison of optimization results over 1 000 generations
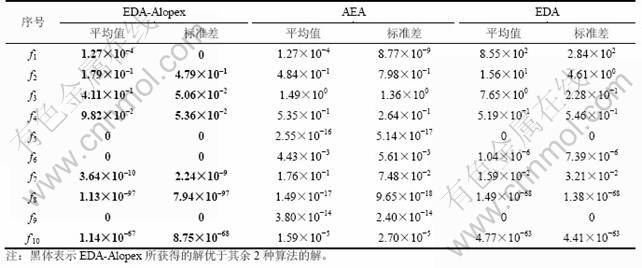
表3 目标函数对应的精度为0.1和最大迭代次数为1 000时运行100次的结果对比
Table 3 Comparison of results of 100 runs when goal accuracy is 0.1 and max generation is 1 000

表4 目标函数对应的精度为0.1和最大迭代次数为2 000时运行100次的结果对比
Table 4 Comparison of results of 100 runs when goal accuracy is 0.01 and max generation is 2 000

表5 目标函数对应的精度为0.01和最大迭代次数为3 000时运行100次的优化结果
Table 5 Comparison of results of 100 runs when goal accuracy is 0.001 and max generation is 3 000

从表3可以看到:EDA-Alopex,AEA和EDA算法在100次连续运行中达到100%收敛的函数个数分别为7,6和5。嵌入了EDA的AEA算法与单一的AEA算法相比,迭代次数和函数调用次数均有大幅度下降,明显提高了AEA算法的效率和收敛速度。EDA算法实现简单,所以,函数调用的次数更少一些,但是,算法的搜索精度不高。
从表3~5可以看到:在3种不同的精度测试中,EDA-Alopex算法在单独运行100次全部到达设定精度的函数个数分别为7,7和7,AEA算法在100次单独计算中100%收敛的函数个数分别为6,6和6,EDA算法100次运行全部收敛到设定精度的函数个数分别为5,4和4。从100次运行算法收敛到设定精度的次数看,EDA-Alopex略好于AEA算法,但EDA-Alopex到达设定精度所需的迭代次数相比AEA算法大幅度减小,算法的效率明显提高。在较为简单的函数寻优中,新算法只需几十次迭代就达到预定的精度,可见收敛速度较快。特别是对于寻优难度较大的Rosenbrock’s Function(即新算法f3),在表3中显示3种算法在 1 000次迭代中均没有收敛到设定值。在表4中,新算法在100次计算中有18次达到了预定精度;表5中,新算法在100次计算中均到达了设定的精度。而对于其他2种算法,即使加大迭代次数也不能达到预定的精度,算法陷入局部最优,改进后的新算法则在加大迭代次数后,搜索能力增强,种群没有过早地陷入局部最优,说明新算法改善了种群多样性,能够有效避免种群过早的陷入局部最优,特别是对复杂函数有较强的寻优能力。
4 EDA-Alopex算法在重油热解模型参数估计中的应用
重油是原油提取汽油、柴油后的剩余的重质油,通过热解,可以生成用途更为广泛的基础化工原料。重油热解过程反应众多,按照反应动力学相似的原则,建立集总反应的动力学模型,可以简化描述复杂反应过程的模型[14]。根据重油热解的三集总反应模型,重油原料热解,首先生成瞬时中间产物M,中间产物M然后生成中间重质馏分W和集总物L,同时,中间重质馏分W也可直接转化为裂解气、轻质馏分和集总物L。
集总模型建立后,对模型中的参数进行准确估计,也有较为重要的实际意义。
本文利用EDA-Alopex算法对重油热解的三集总反应模型进行参数估计,估计数据样本来自文献[14],模型公式如下:

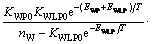
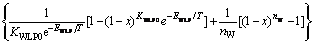 (10)
(10)
式中:x和T为自变量;xL为函数值。根据样本,需要估计的参数有KLP0,ELP,KWP0,KWLP0,EWP,EWLP,nW和nL等8个参数;KLP0为KL0与KP0的比值;ELP为EL和EP之差与R的比值;KWP0为KW0与KP0的比值;KWLP0为KWL0与KP0的比值;EWP为EW与EP之差与R的比值;EWLP为EWL与EP之差与R的比值;nW为瞬时中间物M生成馏分W的反应级数;nL为瞬时中间物M生成集总物L的反应级数。
表6 各种算法给出的重油热解模型参数估计结果
Table 6 Parameter estimation results of heavy oil pyrolysis model given by various algorithms
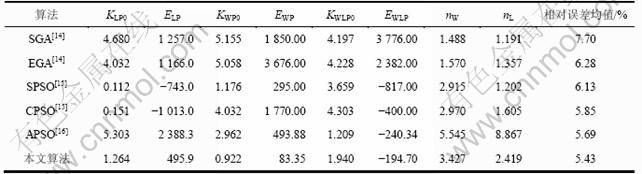
为了与其他文献给出的拟合结果进行对比,同样将种群规模设为50,将56组观测数据全部进行模型的参数估计,得到相对误差均值。本文的计算结果与文献[14]中用简单遗传算法和优进策略改进的遗传算法给出的结果进行比较,与文献[15]中用简单粒子群方法和复合粒子群方法给出的结果进行对比,与文献[16]中采用自适应粒子群算法给出的结果进行了对比。表6所示是各种算法的对比结果。
从表6可以看出:由本文算法所得的相对误差均值为5.43%,相对于改进的粒子群算法CPSO和APSO所得的相对误差更小;与表6中的SPSO,SGA和EGA算法相比,本文算法效果明显优于这3种算法,并且模型参数的拟合误差有较大幅度减小。表明本算法对于复杂非线性函数的寻优能力较强。
5 结论
(1) 本文提出的基于Alopex和分布估计算法融合的进化算法EDA-Alopex,利用EDA算法独特的进化方式来改善AEA算法种群的多样性。这样在EDA-Alopex中,同时获得了EDA提取的整个种群的宏观进化趋势和AEA得到的微观个体之间的一种类似梯度下降的Alopex启发信息,在宏观和微观2个层面同时进化种群,使得算法能够更好地协调全局搜索和局部搜索,与单一算法相比有更高的效率。
(2) EDA-Alopex的收敛速度和获得的解的质量与AEA算法相比都明显提高,表明EDA的引入有效地改善了AEA算法的性能。通过对复杂非线性重油热解三集总模型参数的估计,由本文算法得到的模型参数具有更小的拟合误差,模型参数可以更好地拟合样本数据,表明算法在复杂函数优化问题中有一定的 优势。
参考文献:
[1] Harth E, Tzanakou E. Alopex: A stochastic method for determining visual perceptive fields[J]. Vision Research, 1974, 14(12): 1475-1482.
[2] Bia A. Alopex-B: A new, simpler, but yet faster version of the Alopex training algorithm[J]. International Journal of Neural Systems, 2001, 11(6): 497-507.
[3] Unnikrishnan K P, Venugopal K P. A correlation-based learning algorithm for feed-forward and recurrent neural networks[J]. Neural Computation, 1994, 6(3): 469-490.
[4] 李绍军. 一种基于Alopex的进化优化算法[J]. 模式识别与人工智能, 2009, 22(3): 452-456.
LI Shao-jun. An Alopex based evolutionary optimization algorithm[J]. Pattern Recognition and Artificial Intelligence, 2009, 22(3): 452-456.
[5] Mühlenbein H, Paa? G. From recombination of genes to the estimation of distributions[C]//Mühlenbein H, Bendisch J, Voigt H, et al. The 4th International Conference on Parallel Problem Solving from Nature. Heidelberg: Springer, 1996: 178-187.
[6] 周树德, 孙增圻. 分布估计算法综述[J]. 自动化学报, 2007, 33(2): 113-124.
ZHOU Shu-de, SUN Zeng-qi. A survey on estimation of distribution algorithms[J]. Acta Automatic Sinica, 2007, 33(2): 113-124.
[7] Mühlenbein H, H?ns R. The estimation of distributions and the minimum relative entropy principle[J]. Evolutionary Computation, 2005, 13(1): 1-27.
[8] 张智晟, 时翔, 林涛, 等. 基于分布估计算法和遗传算法融合的神经网络故障诊断模型研究[J]. 电工电能新技术, 2008, 27(3): 18-21.
ZHANG Zhi-sheng, SHI Xiang, LIN Tao, et al. Study of fault diagnosis model based on neural network using estimation of distribution algorithm combined with genetic algorithm[J]. Advanced Technology of Electrical Engineering and Energy, 2008, 27(3): 18-21.
[9] SUN Jian-yong, ZHANG Qing-fu, Edward P K Tsang. DE/EDA: A new evolutionary algorithm for global optimization[J]. Information Sciences, 2005, 169(3/4): 249-262.
[10] Shakya S K. Probabilistic model building genetic algorithm (PMBGA): A Survey[EB/OL]. [2010-06]. http://www.comp. rgu.ac.uk/staff/ss/techReport/Basicsurvey.pdf.
[11] Grahl J, Minner S, Rothlauf F. Behavior of UMDAc with truncation selection on monotonous functions[C]//Proceedings of the 2005 IEEE Congress on Evolutionary Computation (CEC). Scotland: IEEE Press, 2005: 2553-2559.
[12] Pohlhein H. GEA Tbx: Example function (single and multi-objective functions) 1 introduction[EB/OL]. [2010-06]. http://www.geatbx.com/docu/ fcnindex-01.html#P89_3085.
[13] Deep K, Das K N. Quadratic approximation based hybrid genetic algorithm[J]. Applied Mathematics and Computation, 2008, 203(1): 86-98.
[14] 宋晓峰, 陈德钊, 胡上序, 等. 基于优进策略的遗传算法对重油热解模型参数的估计[J]. 高校化学工程学报,2003, 17(4): 411-417.
SONG Xiao-feng, CHEN De-zhao, HU Shang-xu, et al. Eugenic evolution strategy genetic algorithms for estimating parameters of heavy oil thermal cracking model[J]. Journal of Chemical Engineering of Chinese Universities, 2003, 17(4): 411-417.
[15] 俞欢军, 张丽平, 陈德钊, 等. 复合粒子群优化算法在模型参数估计中的应用[J]. 高校化学工程学报, 2005, 19(5): 675-680.
YU Huan-jun, ZHANG Li-ping, CHEN De-zhao, et al. Estimation of model parameters using composite particle swarm optimization[J]. Journal of Chemical Engineering of Chinese Universities, 2005, 19(5): 675-680.
[16] 张项学, 关治洪, 廖锐全. 基于粒子群算法的重油热解模型参数估计[J]. 西安石油大学学报: 自然科学版, 2008, 23(2): 94-98.
ZHANG Xiang-xue, GUAN Zhi-hong, LIAO Rui-quan. Parameter estimation of the thermal cracking model for heavy oil based on particle swarm optimization[J]. Journal of Xi?an Shiyou University: Natural Science Edition, 2008, 23(2): 94-98.
(编辑 陈灿华)
收稿日期:2010-06-05;修回日期:2010-09-09
基金项目:国家自然科学基金资助项目(20976048)
通信作者:李绍军(1970-),男,山东高唐人,博士,研究员,从事化工系统工程、进化计算等研究;电话:021-64253820;E-mail: lishaojun@ecust.edu.cn