DOI: 10.11817/j.issn.1672-7207.2015.03.035
钢筋混凝土氯离子时变扩散及起始锈胀时变可靠度研究
樊玲1,李江腾1,卢文平2,彭述权1,赵军华2
(1. 中南大学 资源与安全工程学院,湖南 长沙,410083;
2. 长江水利委员会 长江科学院,湖北 武汉,430010)
摘要:采用氯离子传感器(MnO2电极为参比电极,Ag/AgCl为工作电极)测量混凝土中氯离子浓度,反演氯离子时变扩散系数幂函数模型,在此基础上研究钢筋混凝土起始锈胀时变可靠度和随机变量敏感性。研究结果表明:所研制的氯离子传感器电位与氯离子浓度有良好线性关系,反演得到的氯离子时变扩散系数随时间增加而减小;采用氯离子时变扩散系数所得的时变失效概率小于氯离子恒定扩散系数所得的时不变失效概率;钢筋保护层厚度对起始锈胀敏感度影响最大,氯离子扩散系数次之;氯离子时变扩散系数速率指数及其收敛值对起始锈胀敏感度影响较大。研究结果对钢筋混凝土起始锈胀时变可靠度预测具有参考作用。
关键词:埋入式氯离子传感器;氯离子时变扩散系数;钢筋混凝土;起始锈胀;时变可靠度;敏感性
中图分类号:TU375 文献标志码:A 文章编号:1672-7207(2015)03-1043-07
Time-dependent chloride diffusion and time-dependent initial corrosion reliability in reinforced concrete
FAN Ling1, LI Jiangteng1, LU Wenping2, PENG Shuquan1, ZHAO Junhua2
(1. School of Resource and Safety Engineering, Central South University, Changsha 410083, China;
2. Changjiang River Scientific Research Institute, Wuhan 430010, China)
Abstract: The embedded chloride sensors with respect to MnO2 reference electrode and Ag/AgCl working electrode were embedded in concrete block soaked in concrete synthetic solution to do the chloride ion diffusion experiment. The powerful function model of time-dependent chloride ion diffusion coefficient in concrete was inversed, and the time-dependent failure probability of initial corrosion of reinforced concrete was predicted and the sensitivity of corresponding variances was analyzed. The results show that the potential of chloride sensor with respect to MnO2 is linear with the chloride concentration, and the time-dependent chloride diffusion coefficient decreases with the increase of time. The probability of initial corrosion by the time-dependent chloride diffusion coefficient is lower than that by the time-independent, the initial corrosion sensitivity of time-dependent chloride diffusion coefficient is less than that of cover, and the effect of the velocity index and convergence value of chloride diffusion coefficient on the initial corrosion sensitivity increases. The results can be referred when the initial corrosion reliability of reinforced concrete is predicted.
Key words: embedded chloride sensors; time-dependent chloride diffusion coefficient; reinforced concrete; initial corrosion; time-dependent reliability; sensitivity
钢筋混凝土起始锈胀是混凝土耐久性研究的一个重要方面,常采用JC法、有限元数值法等[1-2]对其进行时不变可靠度研究[3],采用时间综合法、时间离散法对其进行时变可靠度研究[4-5]。以上方法考虑了氯离子对钢筋腐蚀速率的影响,但计算混凝土中氯离子浓度时,常采用氯离子时不变扩散系数。采用氯离子时不变扩散系数在钢筋混凝土耐久性可靠度分析中存在明显不足。氯离子入侵混凝土是一个非常复杂的过程,受高低温和干湿循环作用、非饱和水毛细水作用、水压力渗透作用、氯离子浓差扩散作用[6]、气候状况[7-8]以及氯离子边界浓度[1]等影响,其中氯离子浓差扩散起主导作用。描述氯离子扩散作用的氯离子扩散系数较难精确测试,是钢筋混凝土起始锈胀可靠度研究的难点。混凝土氯离子扩散系数由混凝土细观结构决定,但混凝土孔隙、微裂缝细观结构复杂,目前无法定量描述,难以通过细观结构分析或试验得到氯离子扩散系数细观表达式[9];同时,随着龄期增加,混凝土细观结构发生改变,混凝土阻碍氯离子扩散能力增强,氯离子扩散系数随时间增加而减小[10],具有时变特征。目前,常采用盐水浸渍稳态或电场非稳态扩散试验[11-12]对混凝土氯离子扩散系数进行测试研究。盐水浸渍稳态试验假定混凝土结构保持不变时氯离子进行自由扩散,测试过程长达1~2 a,在长时间测试过程中没有考虑混凝土细观结构的变化。电场非稳态快速扩散试验加速了氯离子迁移[13, 9],同时也加速了混凝土孔隙溶液中其他离子迁移,因此,测量氯离子扩散系数比实际扩散系数大[13]。以上2种方法均只能测量混凝土中氯离子时不变扩散系数,而不能得到氯离子时变扩散系数。化学传感器技术是测量混凝土中氯离子浓度的一种极具潜力的无损检测方法[14]。在混凝土中埋入电化学传感器,通过实时监测氯离子传感器电化学信息,反演氯离子浓度变化[15-16],在此基础上可获得氯离子时变扩散系数。该测量方法与传感器的电极工作性能密切相关[17]。传感器中参比电极良好的重现性和稳定性有利于减小电极电位测量误差,从而提高氯离子时变扩散系数测量精度[17]。本文作者拟采用自行研发的MnO2参比电极[18],制作埋入式氯离子传感器[19]。通过试验获得氯离子浓度与传感器电极电位的相关关系,运用扩散Fick微分方程反演得到混凝土中氯离子时变扩散系数幂函数模型。在此基础上,采用JC法建立求解钢筋混凝土起始锈胀时变可靠度模型,进而研究氯离子扩散系数、氯离子扩散系数时变模型、极限氯离子浓度、保护层厚度和混凝土表面处氯离子浓度等随机变量对钢筋混凝土起始锈胀可靠度的影响规律。
1 基于埋入式氯离子传感器氯离子时变扩散系数计算方法
由电化学传感器技术可知:在一定氯离子浓度范围内,氯离子传感器电位V与氯离子浓度的对数成正比。依据实测得到的氯离子传感器电位V与氯离子浓度对数lg c(Cl-)间的线性关系(见式(1),运用扩散Fick微分方程(见式(2)),通过堡尔芝曼反演得到混凝土中氯离子时变扩散系数(见式(3))。
 (1)
(1)
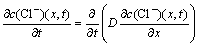 (2)
(2)
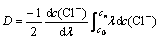 (3)
(3)
式中:系数A和B为试验拟合系数(系数A表征参比电极电位,参比电极不同,电极电位不同;系数B表征氯离子传感器电极电位对氯离子对数浓度的响应系数;在混凝土模拟液和混凝土中,响应系数相同);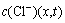 为氯离子浓度;x为计算位置点与混凝土表面之间的距离;t为时间;c0为氯离子初始浓度;cn为t时刻氯离子浓度;D为氯离子扩散系数;λ为反演变换参数,
为氯离子浓度;x为计算位置点与混凝土表面之间的距离;t为时间;c0为氯离子初始浓度;cn为t时刻氯离子浓度;D为氯离子扩散系数;λ为反演变换参数,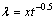 。
。
2 埋入式氯离子传感器氯离子时变扩散试验
2.1 埋入式氯离子传感器
埋入式氯离子传感器为本文作者自行研发的MnO2参比电极[18]与Ag/AgCl工作电极[19]集成,外部用充填硅胶的热塑管密封,端部采用专用透水泥浆布保护,结构图见图1。研发的MnO2参比电极为层状结构,具有良好的重现性和稳定性,在电解质溶液中NaCl浓度为0~2 mol/L时电极电位保持稳定[20]。Ag/AgCl工作电极由纯度为99.99%、直径为0.5 mm、长为10.0 mm的银丝和直径为1.0 mm铜丝锡焊连接而成,采用环氧树脂和树脂套管封装,一端出露部分的银丝在0.1 mol/L盐酸溶液中氯化6 h后形成氯化银包裹层[19]。
在室温下,已知氯离子浓度的混凝土模拟液中,氯离子传感器电极电位(MnO2参比电极与Ag/AgCl工作电极电位差)测试结果见图2。由图2可知:氯离子传感器电极电位受氯离子浓度变化(0~1.0 mol/L)影响较大,受溶液pH变化影响较小。运用matlab得到电极电位拟合式:
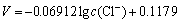 (4)
(4)
其相关性系数为0.997 0,氯离子电极电位响应系数为-0.0692。
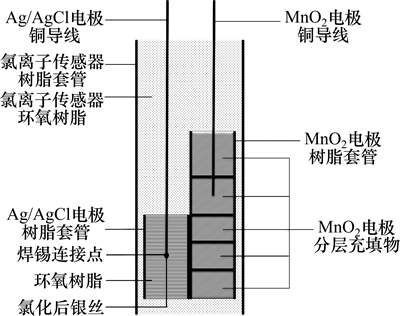
图1 埋入式氯离子传感器结构
Fig. 1 Structure of embedded chloride sensor
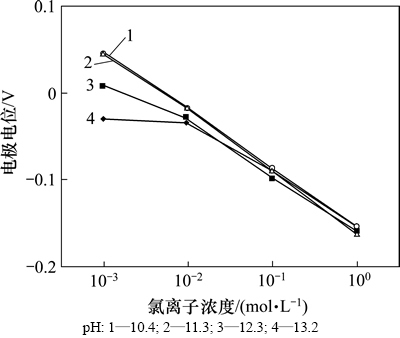
图2 氯离子传感器电位与氯离子浓度的关系
Fig. 2 Relationship between chloride sensor potential and chloride concentration
2.2 混凝土试块中氯离子时变扩散试验方法
将上述埋入式氯离子传感器浸泡在已知氯离子浓度的混凝土模拟液中,测量氯离子传感器电极电位。混凝土模拟液为0.6 mol/L KOH,0.2 mol/L NaOH及饱和Ca(OH)2的混合溶液。调整KOH和NaOH的物质的量比,配制pH为13.5,12.5,11.5和10.5的混凝土模拟液,在以上每一种混凝土模拟液中加入NaCl,配制氯离子浓度分别为2.000,1.000,0.100,0.010和0.001 mol/L的16种混凝土模拟液。制作长×宽×高为100 mm×100 mm×100 mm混凝土试块(配合比水、水泥、砂、石子质量比为0.51:1.00:1.81:3.68)。混凝土试块中氯离子传感器埋设见图3。按图3埋设氯离子传感器。将其浸泡在NaCl浓度为1 mol/L及pH=13的混凝土模拟液中。为控制氯离子只从试块底部扩散进混凝土内部,在试块四周及顶面刷上环氧树脂。
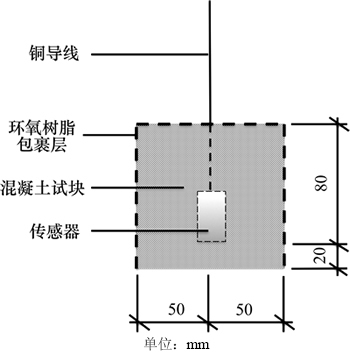
图3 混凝土试块中氯离子传感器埋设图
Fig. 3 Chloride sensor embedded in concrete block
2.3 混凝土试块中氯离子时变扩散试验结果
混凝土试块中氯离子传感器电极电位见图4。由式(4)得到混凝土中氯离子浓度,乘以系数0.035 5得到氯离子质量浓度如图5所示。由式(3)得到混凝土中氯离子时变扩散系数见图6。从图4~6可知:混凝土中氯离子传感器绝对电位随时间增加而增加,相应氯离子质量浓度也随时间增加而增加,反演的混凝土中氯离子扩散系数随时间增加而减小,这与文献[13]中试验结果一致。这是由于混凝土中持续的水化作用导致混凝土细观结构不断发生改变,水泥胶体不断增加,总体上细观孔隙呈减小趋势,从而导致氯离子扩散系数逐渐减小。
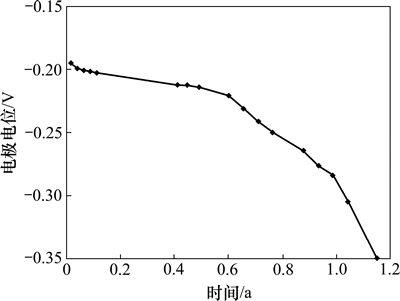
图4 氯离子电极电位与时间的关系
Fig. 4 Relationship between chloride sensor potential and time
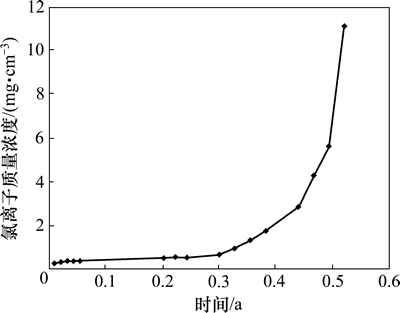
图5 氯离子浓度与时间的关系
Fig. 5 Relationship between chloride ion concentration and time
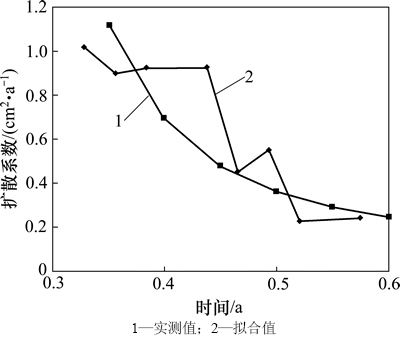
图6 氯离子时变扩散系数与时间的关系
Fig. 6 Relationship between inversed time-dependent chloride diffusion coefficient and time
根据图6中实测氯离子时变扩散系数变化规律,采用以下幂函数进行拟合:
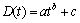 (5)
(5)
式中:D(t)为时变氯离子扩散系数拟合式;a为速率系数;b为速率指数,b小于0;c为收敛值,表征随着时间的增加氯离子扩散系数趋于定值。a和b表征氯离子扩散系数下降速率。拟合结果为
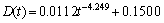 (6)
(6)
对照式(6)与式(5)可知:式(6)中,a=0.011 2,b=-0.424 9,c=0.150 0,相关系数为0.850 0。
3 考虑氯离子时变扩散系数钢筋混凝土起始锈胀时变可靠度
3.1 起始锈胀时变可靠度分析
考虑氯离子时变扩散系数钢筋混凝土起始锈胀时变可靠度控制方程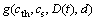 为
为
 (7)
(7)
将式(5)代入式(7)中可得
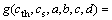
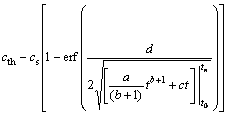 (8)
(8)
式中:erf( )为正态分布函数,即误差函数;cth为临界氯离子浓度;cs为外界电解质氯离子浓度;d为混凝土保护层厚度;tn和t0分别为测试结束时间和起始时间。本文首先考虑cth,cs,D(t)和d组成随机变量向量X,相互独立且服从正态分布,其均值为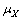 ,标准差为
,标准差为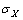 。采用JC法计算时不变可靠度,在“设计验算点”
。采用JC法计算时不变可靠度,在“设计验算点” 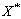 处,极限状态方程g(X)在X*点展开为泰勒级数,取其线性部分。
处,极限状态方程g(X)在X*点展开为泰勒级数,取其线性部分。
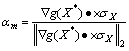 (9)
(9)
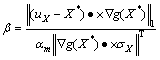 (10)
(10)
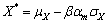 (11)
(11)
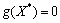 (12)
(12)
式中: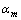 为法线对随机变量的方向余弦,也称敏感度系数;
为法线对随机变量的方向余弦,也称敏感度系数;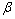 为起始锈胀时不变可靠度;符号“
为起始锈胀时不变可靠度;符号“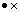 ”表示向量点乘。
”表示向量点乘。
采用迭代法求解可靠度和设计验算点。初始令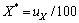 ,计算式(9)和式(11),将式(9)代入式(10)求解得到可靠度,再由式(9)得到迭代后的
,计算式(9)和式(11),将式(9)代入式(10)求解得到可靠度,再由式(9)得到迭代后的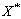 。然后,考虑起始时间点至任意1个时间点ti(i=1, …, n, n为可靠度计算时间,单位为a)区间内可靠度事件相互独立,区间起始锈胀时不变可靠度为
。然后,考虑起始时间点至任意1个时间点ti(i=1, …, n, n为可靠度计算时间,单位为a)区间内可靠度事件相互独立,区间起始锈胀时不变可靠度为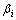 ,相应失效概率为Pi,则该tj(j>i)区间内时变失效概率Pt和时变可靠度
,相应失效概率为Pi,则该tj(j>i)区间内时变失效概率Pt和时变可靠度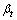 分别为:
分别为:
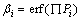 (13)
(13)
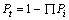 (14)
(14)
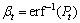 (15)
(15)
3.2 起始锈胀时变失效概率
据文献[2],cth,cs,D(t)和d随机变量取值见表1。采用matlab编写钢筋混凝土起始锈胀时变可靠度分析程序,计算钢筋混凝土起始锈胀时变和时不变失效概率结果,见图7。
表1 随机变量
Table 1 Value of random variable
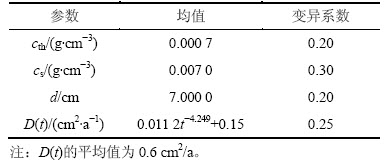
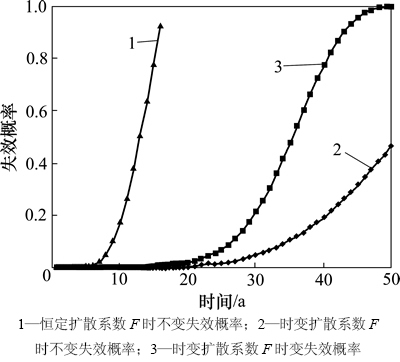
图7 钢筋混凝土起始锈胀失效概率
Fig. 7 Time-dependent failure probability of initial corrosion of reinforced concrete
本文氯离子扩散系数均值为0.600 0 cm2/a。由图7可知:采用氯离子时不变扩散系数计算钢筋混凝土起始锈胀时不变可靠度,可知14 a后起始锈胀失效概率为100%,这一点与文献[2]中计算结果一致;采用氯离子时变扩散系数计算钢筋混凝土时不变可靠度,所得50 a后失效概率仅为43.8%,说明由氯离子时变扩散系数计算得到的钢筋混凝土起始锈胀失效概率减小。采用氯离子时变扩散系数计算钢筋混凝土时变可靠度,所得24 a时起始锈胀失效概率为3.89%,50 a失效概率为99.90%。氯离子时不变扩散钢筋混凝土起始锈胀时不变失效概率最大,氯离子时变扩散钢筋混凝土起始锈胀时变失效概率次之,氯离子时变扩散钢筋混凝土起始锈胀时不变失效概率最小。结合工程结构服役期内氯离子扩散系数时变特征,在工程实践中可采用氯离子时变扩散钢筋混凝土起始锈胀时变失效概率分析模型。
3.3 起始锈胀时变可靠度敏感度
采用式(9)计算氯离子时变扩散系数、临界氯离子浓度、混凝土表面氯离子浓度和保护层厚度等随机变量对起始锈胀可靠度的敏感度,计算结果如图8所示。由图8可知:混凝土保护层厚度对起始锈胀可靠度的敏感度随时间增大而减小,其余随机变量随时间增大而增加。混凝土保护层厚度对起始锈胀可靠度敏感度最大,氯离子时变扩散系数次之,混凝土表面氯离子浓度和临界氯离子浓度最小。因此,分析钢筋混凝土起始锈胀失效概率时,首先要考虑保护层厚度的影响,同时也需要考虑氯离子时变扩散系数的影响。
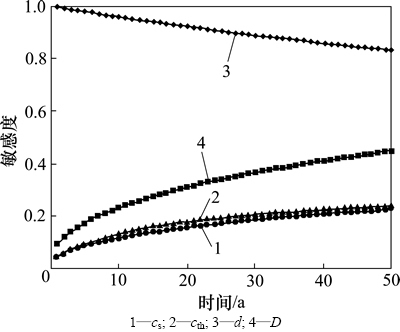
图8 各因素对起始锈胀可靠度的影响
Fig. 8 Effect of random variances on reliability of initial corrosion
式(5)中氯离子时变扩散系数速率系数a、速率指数b和收敛值c对起始锈胀可靠度的敏感度影响如图9所示。由图9可知:起始锈胀可靠度敏感度随a,b和c增加而增加;在初始服役时,b对起始锈胀可靠度敏感度影响最大,a次之,c最小;随服役时间增加, a和b所对应的起始锈胀可靠度敏感度趋于稳定,而c对应的起始锈胀可靠度敏感度趋于发散。因此,在运用电化学传感器技术试验分析氯离子时变扩散系数幂函数参数时,要谨慎确定c和b。

图9 氯离子时变扩散系数模型参数起始锈胀可靠度的敏感度
Fig. 9 Sensitivity of factors of time-dependent chloride diffusion model on reliability of initial corrosion
4 结论
1) 所研发的氯离子传感器电位变化与氯离子浓度变化之间呈良好线性关系。
2) 反演得到的氯离子时变扩散系数随时间增加而减小,考虑氯离子时变扩散,钢筋混凝土起始锈胀时变失效概率小于时不变失效概率。
3) 运用氯离子时变扩散模型进行钢筋混凝土结构起始锈胀可靠度耐久性设计偏于不安全,但运用其进行在役钢筋混凝土结构起始锈胀可靠度分析,所得结果与工程实际结果相吻合。
4) 在起始锈胀时变可靠度敏感度分析中,钢筋保护层厚度敏感度最大,氯离子时变扩散系数敏感度次之。
5) 氯离子时变扩散系数速率指数和收敛值对起始锈胀可靠度敏感度影响较大。采用传感器技术测量氯离子时变扩散系数时,应谨慎确定其速率指数和收敛值。
参考文献:
[1] Ann K Y, Ahn J H, Ryou J S. The importance of chloride content at the concrete surface in assessing the time to corrosion of steel in concrete structures[J]. Construction and Building Materials, 2009, 23(1): 239-245.
[2] Bassem S, Lounis Z. Probabilistic modeling of chloride-induced corrosion in concrete structures using first-and second-order reliability methods[J]. Cement and Concrete Composites, 2012, 34(9): 1082-1093.
[3] Mehta P K. Durability of concrete-fifty years of progress[J]. ACI Special Publication, 1991, 126(1): 1-31.
[4] Akiyama M, Frangopol D M, Yoshida I. Time-dependent reliability analysis of existing RC structures in a marine environment using hazard associated with airborne chlorides[J]. Engineering Structures, 2010, 32(11): 3768-3779.
[5] Guo T, Sause R, Frangopol D M, et al. Time-dependent reliability of PSC box-girder bridge considering creep, shrinkage, and corrosion[J]. Journal of Bridge Engineering, 2010, 16(1): 29-43.
[6] Bastidas-Arteaga E, Chateauneuf A, Sánchez-Silva M, et al. A comprehensive probabilistic model of chloride ingress in unsaturated concrete[J]. Engineering Structures, 2011, 33(3): 720-730.
[7] El Hassan J, Bressolette P, Chateauneuf A, et al. Reliability- based assessment of the effect of climatic conditions on the corrosion of RC structures subject to chloride ingress[J]. Engineering Structures, 2010, 32(10): 3279-3287.
[8] Bastidas-Arteaga E, Chateauneuf A, Sánchez-Silva M, et al. Influence of weather and global warming in chloride ingress into concrete: A stochastic approach[J]. Structural Safety, 2010, 32(4): 238-249.
[9] SUN Guowen, ZHANG Yunsheng, SUN Wei, et al. Multi-scale prediction of the effective chloride diffusion coefficient of concrete[J]. Construction and Building Materials, 2011, 25(10): 3820-3831.
[10] 张宝兰, 卫淑珊. 华南海港钢筋混凝土暴露十年试验[J]. 水运工程, 1999(3): 6-13.
ZHANG Baolan, WEI Shushan. Ten years exposed test of reinforced concrete in south China sea port[J]. Marine Traffic Engineering, 1999(3): 6-13.
[11] Castellote M, Andrade C, Alonso C. Measurement of the steady and non-steady-state chloride diffusion coefficients in a migration test by means of monitoring the conductivity in the anolyte chamber: Comparison with natural diffusion tests[J]. Cement and Concrete Research, 2001, 31(10): 1411-1420.
[12] Pratanu G, Alex H, Paul J T. Prediction of equivalent steady-state chloride diffusion coefficients[J]. ACI Materials Journal, 2011, 108(1): 88-94.
[13] SHI Xianming, XIE Ning, Fortune K, et al. Durability of steel reinforced concrete in chloride environments: An overview[J]. Construction and Building Materials, 2012, 30(5): 125-138.
[14] Bertolini L, Elsener B, Redaelli E, et al. Corrosion of steel in concrete: Prevention, diagnosis, repair[M]. Germany: Wiley-VCH, 2013: 345-373.
[15] Lizarazo-Marriaga J, Claisse P. Determination of the concrete chloride diffusion coefficient based on an electrochemical test and an optimization model[J]. Materials Chemistry and Physics, 2009, 117(2/3): 536-543.
[16] Stanish K, Hooton R D, Thomas M D A. A novel method for describing chloride on transport due to an electrical gradient in concrete: Part 1. Theoretical description[J]. Cement and Concrete Research, 2004, 34(1): 43-49.
[17] FAN Ling, WEI Jun, PENG Shuquan, et al. Performance of manganese oxide reference electrode for concrete monitoring with inner alkaline electrolytes[J]. Applied Mechanics and Materials, 2014, 440: 504-509.
[18] 卫军, 樊玲, 董荣珍. 一种参比传感器: 中国, CN102175734A[P]. 2011-09-07.
WEI Jun, FAN Ling, DONG Rongzhen. A reference sensor: China, CN102175734[P]. 2011-09-07.
[19] 卫军, 刘栋, 樊玲, 等. 一种应用于混凝土内部长期监测钢筋腐蚀状况的传感器装置: 中国, CN102721642A[P]. 2012-10-10.
WEI Jun, LIU Dong, FAN Ling, et al. A kind of long-term monitoring steel corrosion sensor device used in the inside concrete: China, CN102721642A[P]. 2012-10-10.
[20] 樊玲, 卫军, 彭述权, 等. 碱性电解质溶液对埋入式MnO2参比电极性能试验[J]. 武汉理工大学学报, 2013, 35(12): 130-134.
FAN Ling, WEI Jun, PENG Shuquan, et al. Effect of alkaline electrolyte on performance of embedded MnO2 reference electrode[J]. Journal of Wuhan University of Technology, 2013, 35(12): 130-134.
(编辑 陈灿华)
收稿日期:2014-04-10;修回日期:2014-06-22
基金项目(Foundation item):长江科学院开放研究基金资助项目(CKWV2013210/KY);国家自然科学基金资助项目(51374246);长沙市科技计划项目(K1403047-11) (Project(CKWV2013210/KY) supported by the CRSRI Open Research Program; Project(51374246) supported by the National Natural Science Foundation of China; Project(K1403047-11) supported by Planning Project of Science and Technology of Changsha City)
通信作者:彭述权,博士,讲师,从事混凝土耐久性及地下结构混凝土监测、检测研究;E-mail: pqr97linger@csu.edu.cn