Multi-mode process monitoring based on a novel weighted local standardization strategy and support vector data description
来源期刊:中南大学学报(英文版)2016年第11期
论文作者:侍洪波 赵付洲 宋冰
文章页码:2896 - 2905
Key words:multiple operating modes; weighted local standardization; support vector data description; multi-mode monitoring
Abstract: There are multiple operating modes in the real industrial process, and the collected data follow the complex multimodal distribution, so most traditional process monitoring methods are no longer applicable because their presumptions are that sampled-data should obey the single Gaussian distribution or non-Gaussian distribution. In order to solve these problems, a novel weighted local standardization (WLS) strategy is proposed to standardize the multimodal data, which can eliminate the multi-mode characteristics of the collected data, and normalize them into unimodal data distribution. After detailed analysis of the raised data preprocessing strategy, a new algorithm using WLS strategy with support vector data description (SVDD) is put forward to apply for multi-mode monitoring process. Unlike the strategy of building multiple local models, the developed method only contains a model without the prior knowledge of multi-mode process. To demonstrate the proposed method’s validity, it is applied to a numerical example and a Tennessee Eastman (TE) process. Finally, the simulation results show that the WLS strategy is very effective to standardize multimodal data, and the WLS-SVDD monitoring method has great advantages over the traditional SVDD and PCA combined with a local standardization strategy (LNS-PCA) in multi-mode process monitoring.
J. Cent. South Univ. (2016) 23: 2896-2905
DOI: 10.1007/s11771-016-3353-0
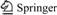
ZHAO Fu-zhou(赵付洲), SONG Bing(宋冰), SHI Hong-bo(侍洪波)
Key Laboratory of Advanced Control and Optimization for Chemical Processes of Ministry of Education
(East China University of Science and Technology), Shanghai 200237, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: There are multiple operating modes in the real industrial process, and the collected data follow the complex multimodal distribution, so most traditional process monitoring methods are no longer applicable because their presumptions are that sampled-data should obey the single Gaussian distribution or non-Gaussian distribution. In order to solve these problems, a novel weighted local standardization (WLS) strategy is proposed to standardize the multimodal data, which can eliminate the multi-mode characteristics of the collected data, and normalize them into unimodal data distribution. After detailed analysis of the raised data preprocessing strategy, a new algorithm using WLS strategy with support vector data description (SVDD) is put forward to apply for multi-mode monitoring process. Unlike the strategy of building multiple local models, the developed method only contains a model without the prior knowledge of multi-mode process. To demonstrate the proposed method’s validity, it is applied to a numerical example and a Tennessee Eastman (TE) process. Finally, the simulation results show that the WLS strategy is very effective to standardize multimodal data, and the WLS-SVDD monitoring method has great advantages over the traditional SVDD and PCA combined with a local standardization strategy (LNS-PCA) in multi-mode process monitoring.
Key words: multiple operating modes; weighted local standardization; support vector data description; multi-mode monitoring
1 Introduction
With the development of market economy, market competition is increasingly stiff. In order to increase the competitive advantage of enterprises, changing product strategies, improving raw materials’ quality etc., are to break away from a single operation mode, resulting in a multi-mode operation condition [1]. The collected data show multi-mode characteristics, and follow multimodal distribution or complex data distribution. Besides, its mean and standard deviation will change when the actual operating mode changes [2]. However, most of the traditional process monitoring methods usually have many data assumptions [3-6], such as only one operating state, sampled data obeying Gaussian or non-Gaussian distribution. The accuracy of process monitoring will decrease if they are unchanged to apply in multi-mode process directly because the sampled data are affected by the outside environment or the system’s internal factors.
To monitor the multi-mode process effectively, ZHAO et al [2] came up with a novel monitoring strategy, which is to build multiple local models. However, it is difficult to obtain the prior knowledge partitioning the training data set effectively in off-line modeling stage. To solve the key problem, more and more clustering methods are designed and applied in the multi-mode process [7-9], which greatly improve the monitoring accuracy. WANG et al [10] developed a new strategy based on transformation probability among different modes to select the most suitable model. SONG et al [11] proposed a clustering method using serial correlations among different variables for multi-mode monitoring. In addition, the optimal criterion, as the core problem, is required to determine for each new sample in online monitoring stage when only a local model is used for multi-mode process. ZHAO et al [2, 12] chose the most optimal local model by the minimum square prediction error (SPE) method. Unlike ZHAO, NATARAJAN et al [13] calculated the minimum distance from a test sample to the training data center for choosing the optimal local PCA model. Nevertheless, if all local models are used for monitoring, an optimal integration strategy will be needed to integrate all local models’ monitoring results [14]. To address this issue, a new integrate strategy combined with Gaussian mixture model, was put forward and applied in multi-mode process monitoring by YU and QIN [15]. At the same time, many more researchers proposed a global modeling method to solve the multi-mode problem. Different from using multiple local models, the fundamental strategy of the global modeling method is to build a suitable model under each operating condition rather than simply acquire the average statistical characteristics of all the data from different modes. For example, according to the hierarchical clustering method, HWANG and HAN [16] proposed a global modeling method based on PCA for multi-mode process monitoring, whereas the global modeling strategy will be effective only when these operating modes are very close, and the nonlinearity of different modes is weak. MA et al [17] built a global monitoring model based on a data standardization method to apply in multimode processes, which obtained the better monitoring results.
Besides, a novel modeling method which is called adaptive modeling is offered and applied in multi-mode process monitoring [18-21]. The core idea is that the mode updates constantly with the changing industrial process. XIE and SHI [22] developed an adaptive monitoring method according to Gaussian mixture model (GMM), which can update model in real-time by tracing the changing process. MA et al [23] developed an updating switch rule, and then proposed an adaptive local modeling scheme based on moving window algorithm. Moreover, the adaptive modeling strategies usually identify the operating conditions by the knowledge of multi-mode process to partition different modes [24]. For example, JIN et al [25] used if-then rules to identify constantly changing modes, which are closely related with actual process knowledge. In addition, KANO et al [26] used external analysis method and process knowledge to identify the operating mode transforms.
Data preprocessing in all monitoring methods is indispensable because the data samples are needed to be standardized before modeling. Up to now, the z-score standardized method has been commonly used in data preprocessing. It can centralize data samples averagely, and standardize all variables to the mean of 0 and the variance of 1, but it cannot change the sampled data distribution. In other words, the multi-mode data standardized by the z-score method still have more than one mode. Support vector data description (SVDD) cannot acquire desirable results on this occasion. In this work, a new weighted local standardization (WLS) strategy is proposed to solve multi-mode problem, then a WLS-SVDD monitoring method is raised to apply in fault detection. Here, the WLS strategy can take out the multi-mode characteristics but does not change the correlation among process variables. So, we can use the standardized training data to build a process monitoring model effectively. In short, some remarkable advantages of the presented method are introduced below. In the stage of data preprocessing, the WLS strategy scales sampled-data into the same distribution, and makes them follow unimodal distribution. Furthermore, in the modeling stage, it just builds a single global model rather than numerous local models. Meanwhile, it does not need to acquire the prior knowledge in advance.
2 Preliminaries
The basic idea of SVDD [27-28] is to construct a minimal hyper-sphere which contains nearly all sampling points. The training data set is assumed to be 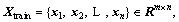 i=1, 2, …, n, which contains n samples and m variables. In order to obtain the minimal hyper-sphere, an SVDD model is built to solve the optimization problem (1).
i=1, 2, …, n, which contains n samples and m variables. In order to obtain the minimal hyper-sphere, an SVDD model is built to solve the optimization problem (1).
 (1)
(1)
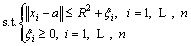
where a and R represent the center and radius of the hyper-sphere, respectively. Furthermore, the slack variable ξi and trade-off parameter C are introduced to improve the accuracy of the algorithm. Subsequently, the above problem is converted into a new Lagrangian form Eq. (2), then we employ the kernel function K(xi·xj) to substitute the computation of inner product (xi·xj). At last, a new dual form Eq. (4) is acquired.

 (2)
(2)
 (3)
(3)
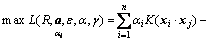
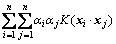 (4)
(4)
The samples xi with αi≥0 computed by Eq. (4) are support vectors. The distance from a to the boundary can be expressed as Eq. (5), where x belongs to support vectors.
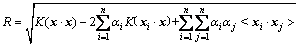 (5)
(5)
3 Multi-mode process monitoring based on WLS-SVDD
3.1 Weighted local standardization strategy
In this section, a novel weighted local standardization (WLS) strategy is proposed to overcome the deficiency of the z-score algorithm in multi-mode process. Different from the z-score algorithm, the proposed WLS strategy utilizes the weighted mean and standard deviation of each sample’s neighbors to standardize the dataset, and make all the variable keep in the same level. Besides, as a univariate normalized method, it does not change the correlation among different variables. For an easier understanding, the reasoning process is introduced in detail as follows.
First, given the training dataset Xtrain={x1, x2, …, xn}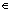 Rm×n, i=1, 2, …, n, then the neighborhood of xi is denoted as N(xi), containing the knn nearest samples from Xtrain, which can be expressed as N(xi)
Rm×n, i=1, 2, …, n, then the neighborhood of xi is denoted as N(xi), containing the knn nearest samples from Xtrain, which can be expressed as N(xi)
 where
where 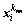 represents the knnth nearest neighbor sample of xi. Meanwhile, the distance mentioned above between xi and
represents the knnth nearest neighbor sample of xi. Meanwhile, the distance mentioned above between xi and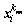 can be represented as
can be represented as  , which is calculated by the Euclidean distance Eq. (6), and then the relationship of all nearest samples’ distance conforms to the inequality (7).
, which is calculated by the Euclidean distance Eq. (6), and then the relationship of all nearest samples’ distance conforms to the inequality (7).
 (6)
(6)
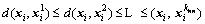 (7)
(7)
The smaller the distance between xi and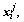 the larger the similarity of
the larger the similarity of  relative to xi. In order to calculate the similarity quantitatively, a weighted vector
relative to xi. In order to calculate the similarity quantitatively, a weighted vector 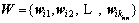 which can be obtained by solving Eqs. (8) and (9) is introduced to express the similarity between different variables.
which can be obtained by solving Eqs. (8) and (9) is introduced to express the similarity between different variables.
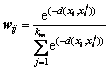 (8)
(8)
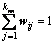 (9)
(9)
For xi (i=1, 2, …, m), the standardized procedure of the WLS strategy is shown below.
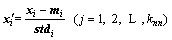 (10)
(10)
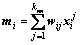 (11)
(11)
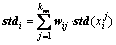 (12)
(12)
where 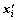 is the normalized sample; mi is the weighted mean; stdi, as the weighted standard deviation, is selected for normalization. In theory, the standard deviation represents the average degree of deviation from the sample centre, and the weighted or un-weighted standard deviation just changes the size of transformed sample, does not change the data position relative to the sample center.
is the normalized sample; mi is the weighted mean; stdi, as the weighted standard deviation, is selected for normalization. In theory, the standard deviation represents the average degree of deviation from the sample centre, and the weighted or un-weighted standard deviation just changes the size of transformed sample, does not change the data position relative to the sample center.
To prove the difference between the z-score method and the WLS strategy, a numerical example is used for analysis and gives a better representation by figures. For simplifying the simulation process, the training dataset is assumed to have three operating modes, which are shown in Eqs. (14), (15) and (16). Moreover, 1500 samples are generated by Eq. (13), so each mode has 500 samples respectively.
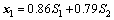 (13)
(13)
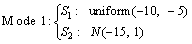 (14)
(14)
 (15)
(15)
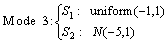 (16)
(16)
As shown in Figs. 1(a) and (b), the original data of x1 have three modes, and follow the multimodal distribution. After scaling by the z-score method, x1 has been scaled to zero mean and unit variance. However, as shown in Figs. 2(a) and (b), the z-score method just changes the data value and probability density of x1, and does not change the multi-mode characteristic and the multimodal distribution. During the data standardization process, the mean value and standard deviation are generated from the whole training dataset by the z-sore method. Figures 1(c) and (d) show that they are fixed global ones, and have different modes. Therefore, the scaled data still obey the multi-mode distribution, which are shown in Figs. 2(a) and (b), and the z-score method won’t get satisfactory results if the training data set has two or more modes.
The WLS strategy is proposed to preprocess the original data, on account of the constantly changing mean and standard variance shown in Figs. 1(c) and (d). The standardization process changes with the mean and the standard deviation of its neighborhood. In the premise of without changing correlations of all the variables, the WLS strategy can be seen as a dynamic standardization method. The data distribution and probability density distribution are shown in Figs. 2(c) and (d). All the data are scaled into the same degree, and follow a unimodal distribution. In a word, the WLS strategy eliminates the multi-mode characteristic successfully.

Fig. 1 Data characteristics of variable 1 and its mean distribution preprocessed by two strategies:
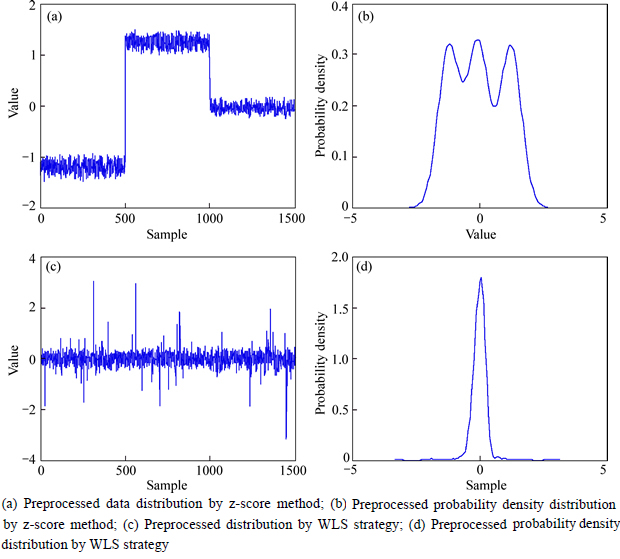
Fig. 2 Data distribution of variable 1 preprocessed by two strategies:
3.2 Process monitoring for multi-mode process based on WLS-SVDD
To solve the multi-mode problem in real industrial process, a novel monitoring method based on WLS- SVDD is proposed. Firstly, the training data are preprocessed by the WLS strategy. Secondly, a SVDD model is built to acquire a hyper-sphere by the normalized data, subsequently calculate the corresponding center and radius, and set the maximum radius as the control limit. Thirdly, the data samples collected online are standardized by the WLS strategy, then the distance from the normalized samples to the hyper-sphere center is calculated to be the new statistics. At last, there will be an alarm if the distance calculated above is greater than the value of radius.
The multi-mode monitoring method is mainly divided into two parts: offline modeling and online monitoring. As shown below, steps 1-4 belong to the offline modeling process, and the rest belong to the online monitoring process.
1) Collect data samples in different operating conditions, and put them into a dataset Xtrain.
2) According to Eq. (6), calculate the distance from xi to each sample in Xtrain to find the knn nearest samples, making up a neighborhood set N(xi).
3) Calculate the weight vector by Eq. (8), then utilize it to acquire the weighted mean and standard deviation of the dataset N(xi) by Eqs. (11) and (12). Finally according to Eq. (10), xi is normalized to  .
.
4) Using the standardized data sample to build the SVDD model for acquiring a hyper-sphere. Then the hyper-sphere’s radius R and the center a are calculated. Meanwhile, R is seen as the control limit.
5) Collect new sample xnew on-line, then find its knn neighbors from Xtrain to constitute a new neighborhood set N(xnew).
6) Use the weighted mean and standard deviation of N(xnew) to normalize xnew, and obtain the normalized sample  .
.
7) Calculate the distance from  to the center of the hyper-sphere, a. Then, set the distance as the new statistic d.
to the center of the hyper-sphere, a. Then, set the distance as the new statistic d.
8) Compare the value of the new statistic d and the control limit R to monitor the process running.
4 Case study
Data preprocessing is essential when SVDD is applied to process monitoring. For different loading in the variances of all variables, only if the variances are normalized to the same scale to make every variables have the same effect in modeling SVDD, which show efficacy in monitoring the industrial process.
In order to verify the validity of WLS strategy, the WLS-SVDD monitoring method is compared with SVDD method and LNS-PCA method in this section. The operating procedures of SVDD method mainly contain two stages. In the modeling stage, the original data are standardized by the z-score method, subsequently used for building the SVDD model. During online monitoring stage, the procedures are as the same as those of WLS-SVDD. The mechanism of LNS-PCA method is similar to the novel proposed monitoring method, and its specific steps can be divided into two parts as follows. Firstly, finding neighborhood of every sample xi is used for normalizing the original data by calculating the neighborhood’s mean and standard deviation, then the model is built based on PCA by using the normalized data, and calculates the corresponding control limit T2. Three methods above are applied to a numerical example and Tennessee Eastman (TE) process both with multi-mode features, and the demonstrated process will be minutely introduced in sections 4.1 and 4.2.
4.1 Numerical example
To demonstrate the validity of the WLS-SVDD monitoring method, a numerical example is chosen and applied in this paper [1]. There are five variables and 800 samples for each variable, which are generated from the following mathematical model (17).
 (17)
(17)
where x1, x2, x3, x4, x5 are the corresponding five variables; s1 and s2 are latent variables; e1, e2, e3, e4 and e5 are white noises whose mean and deviation are 0 and 0.1 respectively. Moreover, two designed modes are shown as follows.
Mode 1:  (18)
(18)
Mode 2: 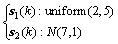 (19)
(19)
Each mode respectively generates 400 samples to constitute the training dataset, so the training dataset contains 800 samples totally. Two test datasets are generated by Eqs. (18) and (19), but introduce with two kinds of faults which will be mentioned below. In the modeling process, the number of neighbor samples is set to 30; the confidence coefficient β and the cumulative percentage P are set to 99% and 85%. Meanwhile, the kernel parameter δ and the parameter C in the SVDD are set as 50 and -0.1.
Fault 1: Firstly, the system runs in Mode 1, then transforms into Mode 2 at the 401th sample. Meanwhile, a step fault of 1 magnitude is loaded to x1 till the end.
Fault 2: In the beginning, the simulation system operates in Mode 1, subsequently changes into Mode 2 at the 401th sample. At the same time, a slope fault of 0.06 magnitude is added to x1 until the last.
As shown in Fig. 3, the data from the numerical simulation have multiple modes and obey the multimodal distribution. Here x1 is preprocessed by the two mentioned preprocessing methods, and Figs. 4 and 5 show the normalized results. It is quite clear that the proposed strategy can eliminate the multi-mode characteristics and the multimodal features of original data, but the z-score method cannot change the data distribution, which proves the presented strategy’s validity.
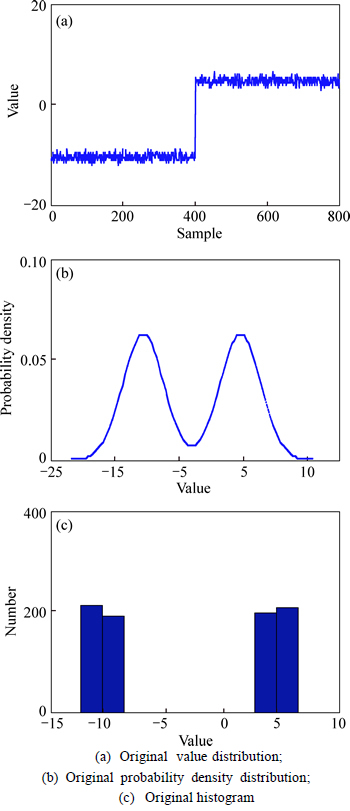
Fig. 3 Original data distribution of x1:

Fig. 4 Normalized distribution of x1 by z-score:
The missed alarm rates (MAR) of two pre-set faults are shown in Table 1. It is easy to see that the MAR of the SVDD monitoring method is too large to suit for multimodal process monitoring. Compared with the SVDD monitoring method, the MAR of LNS-PCA are decreased significantly, but the WLS-SVDD monitoring method gets the best monitoring results. According to the monitoring results of Fault 1, which is shown in Fig. 6, the SVDD method could hardly detect the step fault, causing a large MAR. In contrast to the new raised method, the LNS-PCA method can detect effectively, but it is worse in identifying fault 1. In terms of fault 2, the MAR of T2 in LNS-PCA is 3.25%, obviously lower than that of the SVDD method, but these monitoring results are less than those of the WLS-SVDD method, which is expressed intuitively in Fig. 7.
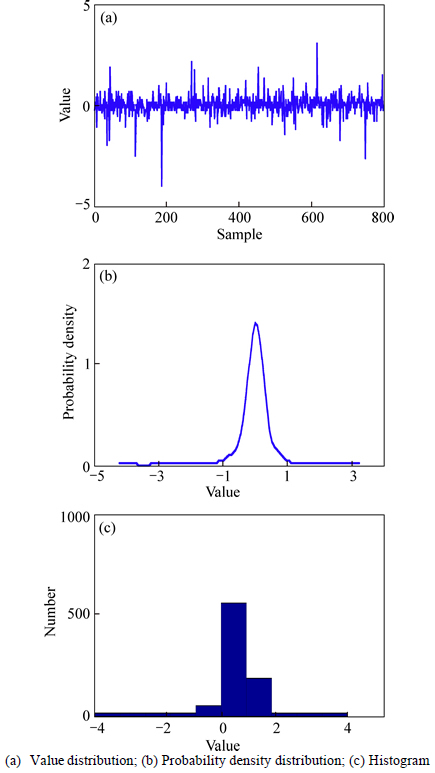
Fig. 5 Normalized distribution of x1 by WLS:
Table 1 MAR of two faults in numerical simulation

In conclusion, according to the comparison between the SVDD method and the WLS-SVDD method, it indicates the effectiveness of the WLS strategy. The comparison of LNS-PCA and the WLS-SVDD illustrates the feasibility of the WLS-SVDD method. In the end, the comparative results on the three methods, show that the monitoring results of the other two methods are not good as those of the proposed method, proving the WLS-SVDD method’s optimality.
4.2 TE process
TE simulation process is widely described and quoted in large number of literatures, and it is mainly composed of five parts, the continuous stirred tank reactor, gas-liquid separator, centrifugal compressor, re-boiler and condenser [29-31]. Meanwhile, the TE process operates in six different modes, and the operating data are generated in different operating conditions, so it has multi-modal characteristics. In addition, the TE process contains 31 monitoring variables, which is constituted by 9 controlled variables and 22 continuous variables.

Fig. 6 MAR for Fault 1 based on three monitoring methods:
In the simulation process, all the data are gathered in Mode 1 and Mode 3. During this period, 20 different faults are imported in the operating process. But the mechanism of faults 16-20 is unknown, and the amplitude of faults 3, 9 and 15 are too small to monitor conveniently. So, there are only remaining 12 faults used for detecting. In the modeling stage, 500 normal data samples are collected in Mode 1 and Mode 3, respectively.

Fig.7 MAR for Fault 2 based on three monitoring methods:
In on-line testing stage, 1000 testing sample are collected in the above two modes separately. Besides, 12 fault points are set at the 1200th test sample point, and the transient process does not take into account between two stable operation modes. In parameter setting process, the value of kernel parameter δ and the parameter C in the SVDD model are set to 50 and -0.1, respectively. knn is set to 50. The cumulative percentage γ in the LNS-PCA monitoring method is 85%, and the control limit β is 99%.
Monitoring results of the three monitoring methods for 12 faults in Mode 3 are shown in Table 2, and the best ones are remarked in boldface. Because these monitoring statistics are built in the primary feature space, so these statistics of T2 and s are only compared in this work. In order to explain the validity of WLS-SVDD method intuitively, some simulation results are represented in a graphical form. It can be seen easily that
Table 2 MAR of fault database in Mode 3
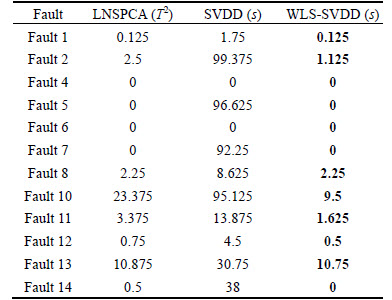
the new presented monitoring method has the optimal monitoring results for almost all faults in Table 2, although LNS- PCA has better monitoring results relative to the SVDD monitoring method. For example, these miss detection rates of Fault 1 and Fault 8 are 0.125% and 2.25%, which are as low as those of WLS-SVDD. In all, as shown in T2 statistics of LNS-PCA, the monitoring performance has been improved. But for all faults, the S statistics show that the WLS-SVDD method has the best performance in comparison to the other two monitoring methods.
Figure 8 shows that in the normal monitoring process, although false alarm rates of LNS-PCA are relatively large, these monitoring results are within permissible range, which proves the feasibility of these three methods. In Fig. 9, the miss alarm rate of SVDD is too large to detect the Fault 10 in Mode 3. The method of LNS-PCA can effectively detect the fault, but compared with the WLS-SVDD method, whose miss alarm rate is still lager, which proves that the new raised method has the best performance for multi-mode process monitoring.
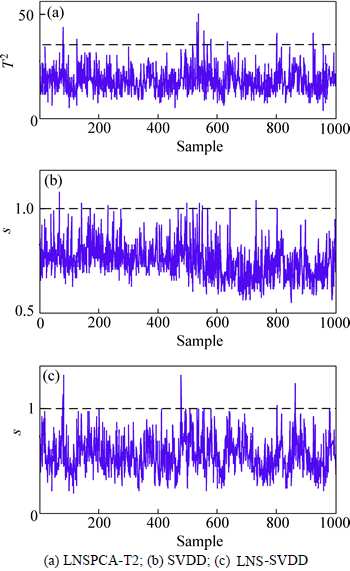
Fig. 8 Monitoring results of normal database:
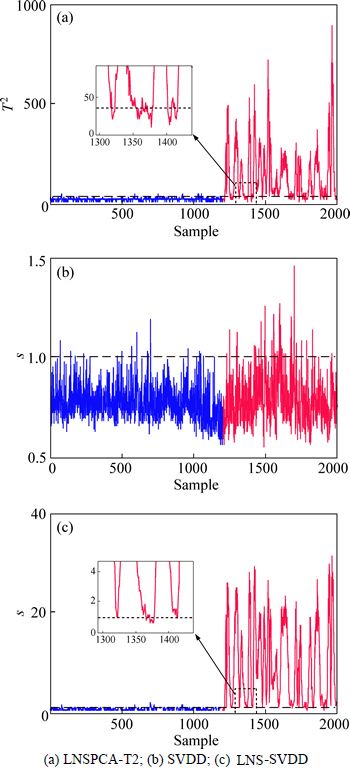
Fig. 9 Monitoring results of Fault 10 in Mode 3:
5 Conclusions
A novel weighted local standardization strategy is proposed to overcome the shortcomings of the traditional z-score preprocess strategy in dealing with multi-mode problems. Subsequently, a new process monitoring method based on WLS-SVDD is put forward to monitor the real industrial processes which are operated in different conditions. Unlike the multiple models for monitoring multi-mode process, the WLS-SVDD monitoring method just has one model, avoiding the defects of the prior knowledge. Firstly, the proposed method is used to normalize the sample data with multi- mode characteristics, then build a SVDD model and calculate monitoring statistics. Finally, a numerical example and TE process are applied to verify the effectiveness of the proposed method. The simulation results indicate that the WLS strategy has obvious advantages in standardizing multi-mode data. Furthermore, compared with the other two monitoring methods, the WLS-SVDD monitoring method has the optimal monitoring performance.
References
[1] GE Zhi-qiang, SONG Zhi-huan. Multimode process monitoring based on Bayesian method [J]. Journal of Chemometrics, 2009, 23(12): 636-650.
[2] ZHAO Shi-jian, ZHANG Jie, XU Yong-mao. Monitoring of processes with multiple operation modes through multiple principle component analysis models [J]. Industrial & Engineering Chemistry Research, 2004, 43(22): 7025-7035.
[3] QIN S J. Statistical process monitoring: Basics and beyond [J]. Journal of Chemometrics, 2003, 17(8): 480-502.
[4] GE Zhi-qiang, SONG Zhi-huan, GAO Fu-rong. Review of recent research on data-based process monitoring [J]. Industrial & Engineering Chemistry Research, 2013, 52(10): 3543-3562.
[5] KRUGER U. Advances in statistical monitoring of complex multivariate processes: With applications in industrial process control [M]. Chichester: Wiley, 2012.
[6] ZHAO Chun-hui, GAO Fu-rong. Fault-relevant principal component analysis (FPCA) method for multivariate statistical modeling and process monitoring [J]. Chemometrics & Intelligent Laboratory Systems, 2014, 133(6): 1-16.
[7] TAN Shuai, WANG Fu-li, PENG Jun, CHANG Yu-qing, WANG Shu. Multimode process monitoring based on mode identification [J]. Industrial & Engineering Chemistry Research, 2012, 51(1): 374-388.
[8] LIU Jia-lin, CHEN Ding-sou. Fault detection and identification using modified Bayesian classification on PCA subspace [J]. Industrial & Engineering Chemistry Research, 2009, 48(6): 3059-3077.
[9] XIE Xiang, SHI Hong-bo. Multimode process monitoring based on fuzzy C-means in locality preserving projection subspace [J]. Chinese Journal of Chemical Engineering, 2012, 20(6): 1174-1179.
[10] WANG Fu-li, TAN Shuai, PENG Jun, CHANG Yu-qing. Process monitoring based on mode identification for multi-mode process with transitions [J]. Chemometrics & Intelligent Laboratory Systems, 2012, 110(1): 144-155.
[11] SONG Bing, SHI Hong-bo, MA Yu-xin. Multi-subspace principal component analysis with local outlier factor for multimode process monitoring [J]. Industrial & Engineering Chemistry Research, 2014, 53(42): 16453-16464.
[12] ZHAO Shi-jian, ZHANG Jie, XU Yong-mao. Performance monitoring of processes with multiple operating modes through multiple PLS models [J]. Journal of Process Control, 2006, 16(7): 763-772.
[13] NATARAJAN S, SRINIVASAN R. Multi-model based process condition monitoring of offshore oil and gas production process [J]. Chemical Engineering Research and Design, 2010, 88(5/6): 572-591.
[14] MA He-he, HU Yi, SHI Hong-bo. Fault detection and identification based on the neighborhood standardized local outlier factor method [J]. Industrial & Engineering Chemistry Research, 2013, 52(6): 2389-2402.
[15] YU Jie, QIN S J. Multimode process monitoring with Bayesian inference-based finite Gaussian mixture models [J]. AIChE Journal, 2008, 54(7): 1811-1829.
[16] HWANG D H, HAN C H. Real-time monitoring for a process with multiple operating modes [J]. Control Engineering Practice, 1999, 7: 891-902.
[17] MA He-he, HU Yi, SHI Hong-bo. A novel local neighborhood standardization strategy and its application in fault detection of multimode processes [J]. Chemometrics & Intelligent Laboratory Systems, 2012, 118(7): 287-300.
[18] TEPPOLA P, MUJUNEN S P, MINKKINEN P. Adaptive fuzzy C-means clustering in process monitoring [J]. Chemometrics and Intelligent Laboratory Systems, 1999, 45(1/2): 23-38.
[19] CHOI S W, MARTIN E B, MORRIS A J, LEE I B. Adaptive multivariate statistical process control for monitoring time-varying processes [J]. Industrial & Engineering Chemistry Research, 2006, 45(9): 3108-3118.
[20] GE Zhi-qiang, SONG Zhi-huan. Online monitoring of nonlinear multiple mode processes based on adaptive local model approach [J]. Control Engineering Practice, 2008, 16(12): 1427-1437.
[21] SONG Bing, MA Yu-xin, SHI Hong-bo. Multimode process monitoring using improved dynamic neighborhood preserving embedding [J]. Chemometrics & Intelligent Laboratory Systems, 2014, 135(14): 17-30.
[22] XIE Xiang, SHI Hong-bo. Dynamic multimode process modeling and monitoring using adaptive Gaussian mixture models [J]. Industrial & Engineering Chemistry Research, 2012, 51(15): 5497- 5505.
[23] MA Yu-xin, SHI Hong-bo, WANG Meng-ling. Adaptive local outlier probability for dynamic process monitoring [J]. Chinese Journal of Chemical Engineering, 2014, 22(7): 820-827.
[24] LEE Y H, JIN H D, HAN C H. On-line process state classification for adaptive monitoring [J]. Industrial & Engineering Chemistry Research, 2006, 45(9): 3095-3107.
[25] JIN H D, LEE Y H, LEE G, HAN C H. Robust recursive principal component analysis modeling for adaptive monitoring [J]. Industrial and Engineering Chemistry Research, 2006, 45(2): 696-703.
[26] KANO M, HASEBE S, HASHIMOTO I, et al. Evolution of multivariate statistical process control: Application of independent component analysis and external analysis [J]. Computers and Chemical Engineering, 2004, 28(6/7): 1157-1166.
[27] TAX D M J., DUIN R P W. Support vector domain description [J]. Pattern Recognition Letters, 1999, 20: 1191-1199.
[28] TAX D M J., DUIN R P W. Support vector data description [J]. Machine Learning, 2004, 54: 45-66.
[29] DOWNS J J, VOGEL E F. A plant-wide industrial process control problem [J]. Computers and Chemical Engineering, 1993, 17(3): 245-255.
[30] RICKER N L. Optimal steady-state operation of the Tennessee Eastman challenge process [J]. Computers & Chemical Engineering, 1995, 19(9): 949-959.
[31] WANG Li, SHI Hong-bo. Multivariate statistical process monitoring using an improved independent component analysis [J]. Chemical Engineering Research & Design, 2010, 88(4): 403-414.
(Edited by YANG Hua)
Foundation item: Project(61374140) supported by the National Natural Science Foundation of China
Received date: 2015-08-08; Accepted date: 2015-11-15
Corresponding author: SHI Hong-bo, Professor; Tel: +86-21-64252189; E-mail:hbshi@ecust.edu.cn

