Numerical study of RC beams under various loading rates with LS-DYNA
来源期刊:中南大学学报(英文版)2018年第5期
论文作者:Leila MAJIDI Nima USEFI Reza ABBASNIA
文章页码:1226 - 1239
Key words:strain rate; dynamic loading; RC beam; impact loading; finite element; LS-DYNA
Abstract: Having an accurate understanding of concrete behavior under effects of high strain rate loading with the aim of reducing incurred damages is of great importance. Due to complexities and high costs of experimental research, numerical studies can be an appropriate alternative for experimental methods. Therefore, in this research capability of the finite element method for predicting concrete behavior at various loading conditions is evaluated by LS-DYNA software. First, the proposed method is presented and then is validated in three stages under different conditions. Results of load–midspan displacement showed good agreement between experimental and finite element results. Capability of finite element method in analyses of beams under various rates of loading was also validated by low error of the results. In addition, the proposed method has reasonable ability to evaluate reinforced concrete beams under various loading rates and different conditions.
Cite this article as: Leila MAJIDI, Nima USEFI, Reza ABBASNIA. Numerical study of RC beams under various loading rates with LS-DYNA [J]. Journal of Central South University, 2018, 25(5): 1226–1239. DOI: https://doi.org/ 10.1007/s11771-018-3820-x.

J. Cent. South Univ. (2018) 25: 1226-1239
DOI: https://doi.org/10.1007/s11771-018-3820-x

Leila MAJIDI1, Nima USEFI2, Reza ABBASNIA1
1. Civil Engineering Department, Iran University of Science and Technology, Tehran 16846-13114, Iran;
2. Centre for Infrastructure Engineering, Western Sydney University, Sydney 2747, Australia
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract: Having an accurate understanding of concrete behavior under effects of high strain rate loading with the aim of reducing incurred damages is of great importance. Due to complexities and high costs of experimental research, numerical studies can be an appropriate alternative for experimental methods. Therefore, in this research capability of the finite element method for predicting concrete behavior at various loading conditions is evaluated by LS-DYNA software. First, the proposed method is presented and then is validated in three stages under different conditions. Results of load–midspan displacement showed good agreement between experimental and finite element results. Capability of finite element method in analyses of beams under various rates of loading was also validated by low error of the results. In addition, the proposed method has reasonable ability to evaluate reinforced concrete beams under various loading rates and different conditions.
Key words: strain rate; dynamic loading; RC beam; impact loading; finite element; LS-DYNA
Cite this article as: Leila MAJIDI, Nima USEFI, Reza ABBASNIA. Numerical study of RC beams under various loading rates with LS-DYNA [J]. Journal of Central South University, 2018, 25(5): 1226–1239. DOI: https://doi.org/ 10.1007/s11771-018-3820-x.
1 Introduction
A wide range of structures such as tall buildings, bridges, tunnels, dams and military shelters are built with reinforced concrete (RC) elements. In the literature, performance of concrete under static loading has been studied extensively. However, during service life of RC structures, they may be subjected to dynamic loads such as earthquake, wind or impact. Hence, studying the behavior of RC members under high strain rate loading is really fundamental. Nowadays, experimental testing and numerical modelling of RC elements at high loading rates are the main attention of many researchers.
Some researchers [1–4] studied the behavior of concrete under high rate loading using Split Hopkinson pressure bar which is employed for impact test. YAN et al [5] carried out several direct dynamic experiments with strain rates of 10–5– 10–0.3 s–1 and investigated the effects of strain rate on tensile strength, elastic modulus, critical strain and energy absorption of concrete. A number of researchers implemented numerous experimental studies on tensile and compressive strength of concrete at various strain rates, in which their results are included in the study of BISCHOFF et al [6] and can be seen in Figure 1.
Many studies have been also conducted in order to evaluate RC elements under high rate loads. KULKARNI et al [7] carried out some experimental tests at various rates of concentrated loading and reported the effects of strain rate on the behavior of RC beams. REMENNIKOV et al [8] tested some scaled RC columns with unique cross section and different rebars under static and impact loads. A series of comprehensive experimental tests on RC beams under impact loading with drop weight were implemented by HUGHES et al [9].
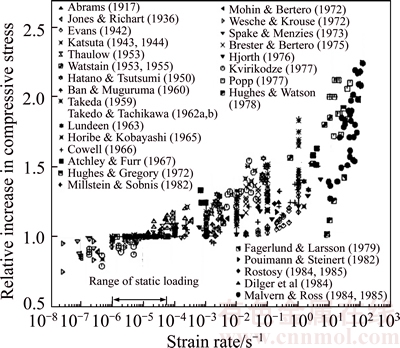
Figure 1 Effect of strain rate on compressive strength [6]
Their results showed that most of the beams experience a flexural failure and crack pattern is distributed along the beam length. WEERHEIJM et al [10] presented the results of dynamic tensile strength and fracture energy at loading rates more than 1000 GPa/s. TACHIBANA et al [11] conducted some impact loading tests on RC beams and presented crack pattern, impact force and mid- span deflection for the beams. SAATCI et al [12] applied impact load with drop weights of 211 and 600 kg on four RC beams and studied the influence of shear mechanism and pattern of crack propagation. Some researchers [13, 14] also utilized both experimental and analytical studies in order to investigate the behavior of RC beams under impact loads. XIAO et al [15] also evaluated the effect of high rate loading on failure mode and mid-span deflection of RC beams using experimental tests. GOLDSTON et al [16] and QASRAWI et al [17] also evaluated the effects of the retrofitting systems on the behavior of concrete beams under impact load.
The past studies on the RC beams under high strain rate loading indicate that most of previous researches have been implemented experimentally and further investigation is required in numerical and analytical approaches. Since experimental testing is time-consuming and expensive, finite element (FE) simulations can be a valuable alternative method for experimental tests. Therefore, proposing a comprehensive FE method which is accurate and simple is the main aim of this study. To reach this goal, a FE method for studying the behavior of RC beam under varying rates of loading (static and high rate loads) is presented and the proposed method is evaluated in three different conditions. 23 beams are analyzed to investigate the influence of stirrup, beam span, loading span and real impact scenario on the result of proposed method. Three-dimensional FE models of RC beams are verified with the experimental data [7, 13, 14] in all three steps. This study is also aimed to propose a simple FE method based on LS-DYNA to predict the dynamic behavior of RC beams under varying rates of loading and to investigate the capability of the proposed model by considering the influence of strain rate.
2 Finite element framework
LS-DYNA is a powerful finite element software which is utilized for simulation of complicated dynamic phenomena [18]. First, the details of modelling such as material properties, mesh details and boundary conditions are presented. Then, the proposed method is validated in three different conditions. A simple FE model of Split Hopkinson bar is also employed for applying the strain rate formulations to the LS-DYNA, and the results are verified with experimental data.
2.1 Material properties
Many models are available for simulation of concrete in FE software [19–24]. In this study, Concrete Damage REL3 (MAT072 RL3), which was proposed by CRAWFORD et al [20], is used for simulation of concrete. This model is a three-invariant model that considers damage and strain rate effects. It uses three surfaces of shear failure, and is developed based on the pseudo- Tensor model. The total stress is divided into isotropic and deviatoric stress in this model. In general, comparing with other models, K&C model is more appropriate for simulation of RC structures exposed to various static, quasi-static, dynamic, seismic and impact loads.
Resistance surfaces: Three stress surfaces for this model are shown in Figure 2(a) [19]. This model is dependent on several parameters and choosing the correct value would cause accurate results. Eight coefficients of a0 to a8 are required to determine resistance surfaces which are obtained from experimental data. In addition, coefficients b 2 and b3 control softening of material and are also obtained from experimental data [25].
Dependence on scale and speed: The K&C model controls shear damage accumulation by the effects of speed. Strain rate increase factor (RF) or dynamic increase factor (DIF) is also used for scaling the stress surfaces when materials are exposed to high rate loads. New increased surfaces in the current pressure are obtained from Eqs. (1) and (2) and are graphically depicted in Figure 2(b) [19].
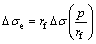 (1)
(1)
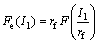 (2)
(2)
where rf is strain rate increase factor; p is pressure and △σe is the increased resistance; 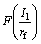 is the unenhanced shear strength; p/rf is the unenhanced pressure.
is the unenhanced shear strength; p/rf is the unenhanced pressure.
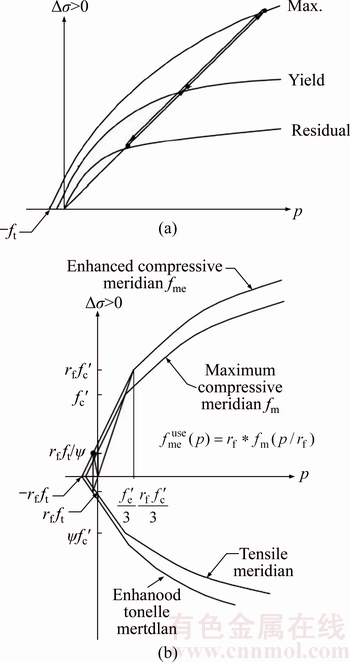
Figure 2 Resistance surfaces [19] (a) and effects of strain rate on resistance surfaces [19] (b) (ft: compressive strength; f′c: tensile strength; ψ: ratio of tensile to compressive meridian radii at a given pressure)
The PIECEWISE_LINEAR_PLASTICITY (MAT_024) material was employed for modelling of rebar. An elasto-plastic material with specified stress–strain data and strain rate dependency can be defined in this model; and failure can be considered based on a plastic strain or a minimum time step size.
2.2 Element type
Solid element was utilized for modelling of concrete. Beam element with both Truss and Hughes-Liu feature can be used for rebar modelling. Hughes-Liu element was used in this study for simulation of rebar.
2.3 Concrete and rebar interaction
The bond-slip effect is an important feature that needs to be considered in developing computational models. If bond-slip is neglected, the model cannot capture the bond failure mode. For interaction between concrete and reinforcing bars, bond-slip behavior was modeled by defining a one-dimensional contract interface between solid elements (representing concrete) and beam elements (representing reinforcing bars). The bond- slip relationship is assumed to be bilinear, and bond stress deterioration after reaching a maximum bond stress is considered through setting a positive value of the exponent in the damage curve. Two groups of points are required for modelling bond-slip. The first group is for concrete points in direction of reinforcing bars and the second group is for the points of reinforcing bars.
2.4 Applying strain rate effects in FE modelling
Many researchers have presented various theoretical and experimental relationships for the influence of strain rate on concrete resistance [26–33]. For considering this effect, Malver relationships are more reliable and applicable than other relations. The relations are presented in the following:
2.4.1 Influence of strain rate on compressive strength of concrete [32]
International Federation for structural concrete has evaluated the effects of strain rate on compressive behavior of concrete. This research which was carried out by MALVER and CRAWFORD [32–36], investigated the effects of strain rate on elastic modulus of concrete and dynamic increase factor. Following equations are presented for concrete in compression:
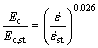 (3)
(3)
 (4)
(4)
where Ec is elastic modulus in strain rate  Ec,st is static elastic modulus; fc is compressive strength of concrete;
Ec,st is static elastic modulus; fc is compressive strength of concrete; 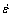 is strain rate;
is strain rate; 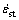 is static strain rate equal to 3×10–5 s–1 and lgγs=6.15αs–2, αs=1/(5+
is static strain rate equal to 3×10–5 s–1 and lgγs=6.15αs–2, αs=1/(5+ 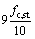 ).
).
2.4.2 Influence of strain rate on tensile strength of concrete [32]
Although tensile strength of concrete has low effect on concrete resistance, this effect was also considered in this study for the accuracy of calculations. The presented equations for concrete in tension under the effect of strain rate are as follows:
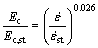 (5)
(5)
 (6)
(6)
where Ec is elastic modulus in strain rate  Ec,st is static elastic modulus; ftis tensile resistance of concrete;
Ec,st is static elastic modulus; ftis tensile resistance of concrete; 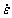 is strain rate;
is strain rate;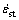 is static strain rate equal to 3×10–6 s–1 and 1gβs=7.11δs–2.33, δ=1/(5+6fc,st/107).
is static strain rate equal to 3×10–6 s–1 and 1gβs=7.11δs–2.33, δ=1/(5+6fc,st/107).
2.4.3 Influence of strain rate on steel strength [33]
Elastic modulus of steel is independent of strain rate and has a constant value; but yield and ultimate strength are dependent on the strain rate. The relations for tension and compression are similar. The effect of strain rate on steel behavior is presented as following equations:
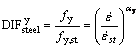 (7)
(7)
 (8)
(8)
where fy is yield resistance of steel in strain rate 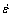 ; fy,st is static yield resistance of steel; fu is final resistance in strain rate
; fy,st is static yield resistance of steel; fu is final resistance in strain rate fu,st is static final resistance of steel;
fu,st is static final resistance of steel; 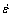 is strain rate;
is strain rate; 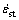 is static strain rate equal to 10–4 s–1,
is static strain rate equal to 10–4 s–1, 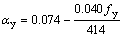 and
and 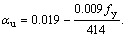
2.4.4 Applying strain rate formulation to LS_DYNA
Considering the results of previous researchers, the CEB relations can be used in the LS-DYNA for modelling of strain rate effects; capability and accuracy of these relations were also evaluated by a separate FE model. Hence, a Hopkinson bar was simulated in LS-DYNA as shown in Figure 3. The material and the boundary condition for this bar are similar to the bar in study of RIISGAARD et al [27]. The bar was exposed to impact load due to the effect of impact bar. Impact rate was increased in each step and the result of strain rate was obtained from the bar.

Figure 3 Three-dimensional FE model of split Hopkinson bar
Figure 4 indicates numerical results obtained from FE model in comparison with experimental data. As good agreement is seen between the numerical and experimental results, the Malver relations were applied to LS_DYNA for consideration of the effects of strain rate on concrete under high rate loading.
Figure 4 Validation of Hopkinson bar results with numerical data
3 Validation of proposed model
Three steps are utilized for validation of proposed FE model, and in each step the capability of model in specific condition is evaluated. In the first step, FE model is evaluated in condition of stirrup change. In the second step, beam length and load span changes are considered for further evaluation of the proposed FE method. In the third step, a real condition of impact load is simulated in order to validate the proposed FE method under high rate loads.
3.1 First step: Validation of FE model with change of stirrup
In this step, the proposed FE method is validated based on different stirrups configurations. Nine RC beams with similar boundary conditions and geometry, but with different numbers of stirrups, were exposed to three different loading rates and the results were verified with experimental data [14]. Table 1 indicates the properties of the beams. Loading was applied in three rates of static, moderate (400 mm/s) and high speed (2000 mm/s). Table 2 shows the geometry, mesh size, FE simulation and boundary conditions of the RC beams.
Load–midspan deflection results of the specimens under three different loading rates are shown in Figures 5–7. As it is seen from experimental data and FE results, load capacity is increased in all three beams by increasing the load rate. This enhance of preliminary resistance in experiment is due to the effects of strain rate on the materials which are applied naturally to the RC members during an experimental test. Since the proposed model considers the effects of strain rate, the increase of resistance in FE results is also justifiable. In general, FE results have reasonable agreement with experimental data. Increase of beam strength by increasing load rate in specimen B1, with no stirrup, is more than specimens B2 and B3. In other words, the effect of load rate on beams with less shear resistance (without stirrup) is more than on high shear resistance beams.
In specimen B1, for all loading rates, the resistance capacity of the beam reached to a maximum strength, and then the resistance decreased. Although the fluctuation of the strength at high loading rate was more than static loading, the general behavior of the curves in all three types of loading was descending after reaching a maximum capacity. In the specimen B2, sudden decrease of strength was less than specimen B1 and the residual resistance was more than specimen B1. Also for static loading on this specimen, results showed a plastic behavior after reaching to a maximum capacity. Area under the force–displacement curve, which represents energy absorption, also indicates that energy absorption in B2 is more than B1. In specimen B3, for all three rates of loading, the specimen reached to a maximum strength and remained approximately stable in that mood. Hence, with increasing the shear resistance of the beams, residual resistance of them is increased. The maximum strength in each specimen also was increased by both adding more stirrups and increasing the loading rate. In general, by increasing the shear resistance of the beams, the shear failure converted to bending failure and better consistency was observed between FE and experimental results.
Table 1 Details of RC beams in first step

Table 2 Geometry details and FE simulation of beams
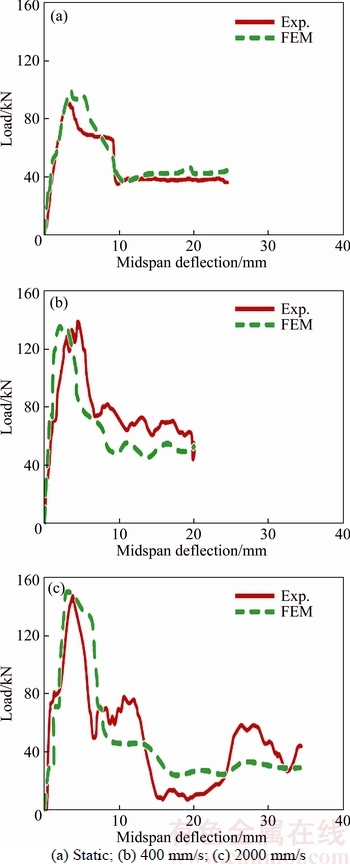
Figure 5 Comparison of load–midspan deflection for specimen B1 under three different loading rates
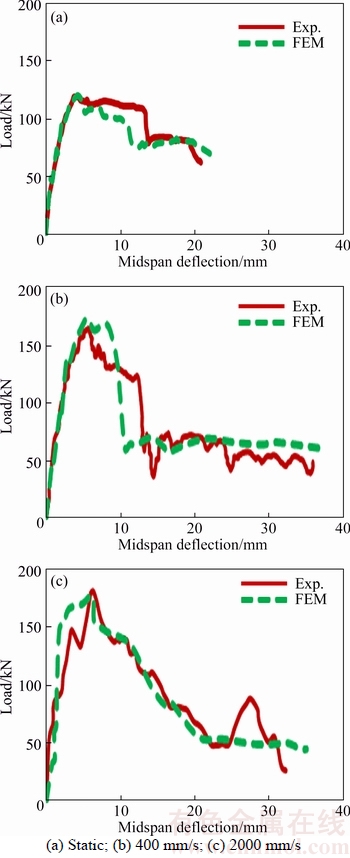
Figure 6 Comparison of load–midspan deflection of specimen B2 under three different loading rates
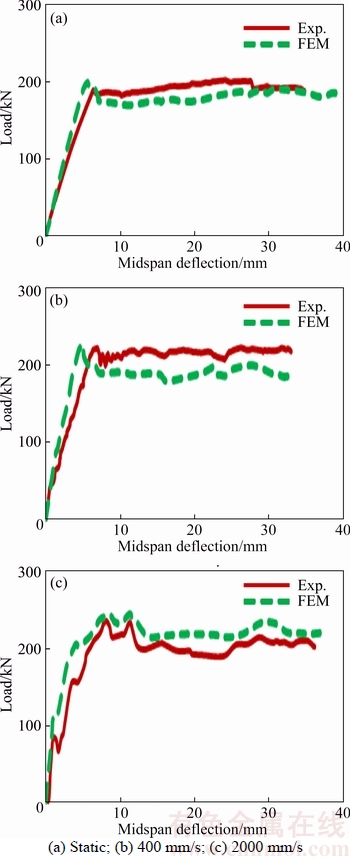
Figure 7 Comparison of load–midspan deflection of specimen B3 under three different loading rates
Error between FE and experimental results of maximum strength was calculated for a better understanding of the accuracy of the proposed method. The error was calculated by Eq.(9) and the results are presented in Table 3.
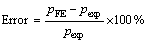 (9)
(9)
Based on the error, results of maximum strength predicted by FE method have less than 12% error compared to experimental data. Since the interaction of rebar and concrete in FE method is not modeled accurately when it is in the experimental test, the discrepancy of the results and the calculated errors are justifiable. In addition, in the FE method, concrete is defined as a homogenous material which has unique resistance in the whole specimen, but this condition cannot happen in experimental tests [35, 36].
Table 3 Error values under three loading rates

3.2 Second step: Validation of FE method with changes of beam and load span:
In this step, the proposed FE method is validated by beams with different lengths and different loading spans at high rate and static loading. Details of the specimens are presented in Table 4 and more details can be found in Ref. [7]. The geometry, boundary conditions and FE simulation with mesh size are also depicted in Figure 8.
Figure 9 shows the FE results of the beams at both static and high rate loading and are compared with experimental data. The peak load and the area under the load–deflection curve (absorbed energy) increased with the increase of the loading rate. In most specimens, FE results at high rate loading were higher than other three curves which indicate that the proposed FE method extracts more resistance for high rate loading compared to experimental condition. As mentioned before, this can be due to the interaction between concrete and rebar and the homogeneity of concrete in FE specimens. In specimens B6, B5 and B9, the behavior of beams at static and high rate loading was similar. With the increase of loading, beam strength reached to its maximum capacity and then remained approximately constant in their plastic behavior. In addition, the bar failure did not occur in these beams and all four curves had a same pattern.
Flexural failure is characterized by crushing of concrete in the compression zone between the load points. After reaching to a maximum strength in flexural failure, the load–midspan deflection curve of beam showed a relatively gradual reduction of strength with increasing deflection. On the other hands, shear failure is characterized by a predominant shear crack in one half of the span. After reaching to a peak strength, the load–midspan deflection curve of beam showed a very sharp decrease in the strength capacity. In specimens B7, B8 and B10, the failure mode occurred earlier at static condition than high rate loading. In fact, in these beams shear failure was dominant at static loading and flexural failure occurred at high strain rate conditions. In specimen B11, due to the very short beam span compared to other specimens, early shear failure was observed at both high strain rate and static conditions. The specimen showed better resistance at high strain rate state which is justifiable based on strain rate effects on concrete. Mode of failure can also change due to the beam span [37] (shear failure for short span and flexural failure for long span) which is seen in some specimens.
Table 4 Details of beams in second step
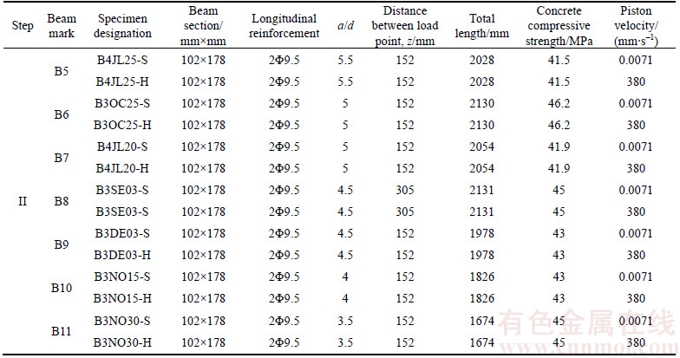
Figure 8 Geometry details [7] (a) and FE simulation of beam (b)
Figure 10 indicates the damage index for B7, B8, B10 and B11 both in experimental [7] and FE models. This damage index shows the propagation of cracks and the amount of failure in beams at static and high rate loads.
Comparison of cracking pattern of the beams in experimental and numerical model shows that proposed FE method has also the ability of showing damage index and crack propagation of the beams. Total number of cracks also decreased significantly with the increase of loading rate. At static condition, the cracks have enough time to spread into the beam and find the weakest part of the concrete such as cement. Nevertheless, large amount of energy is conducted in the beams at the high loading rates, and cracks can also pass through strong parts of the beams such as aggregates in a very short time. In general, development and range of crack propagation were limited at high rate loading compared to the static loading, but the magnitude of failure and crack width at static loading were higher than high rate loading. The number of cracks at static loading was more than those under the number of cracks at high rate loading condition. The red color in the damage index represents the critical parts of the specimen and this red color is seen more often at high rate loading than static loading.
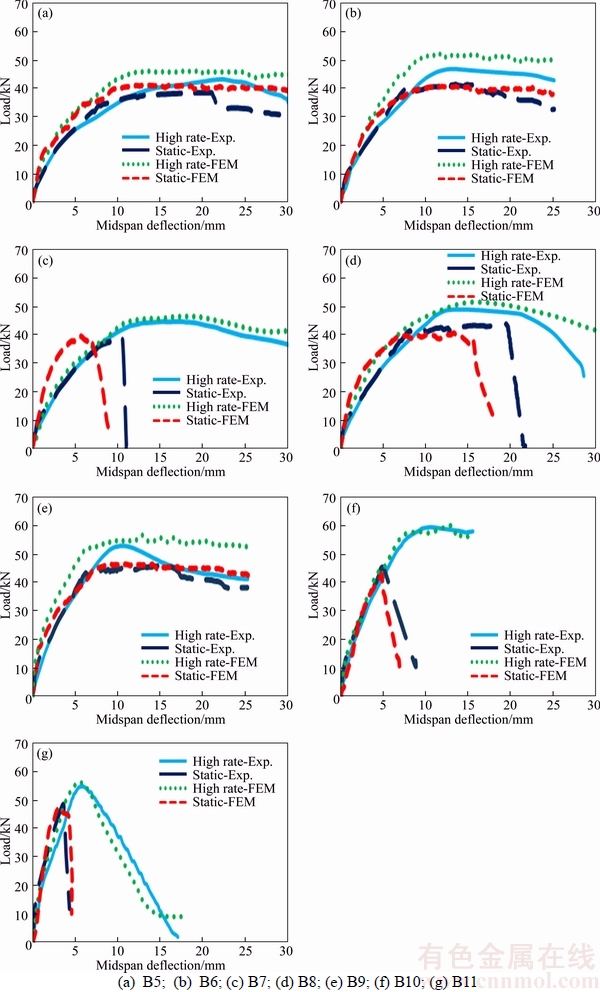
Figure 9 Load–midspan deflection of beams of second step

Figrue 10 Propagation of cracks and amount of failure in beams
3.3 Third step: Validation of FE method with a real impact scenario
Experimental data of the specimen B3 were utilized for studying the capability of the proposed method in a real impact loading [13]. In this test, a drop hammer with mass of 400 kg was dropped freely onto the top surface of the RC beam at mid span from three different heights of 0.3, 0.6 and 1.2 m. For FE modelling, a ball with the same conditions was used instead of hammer. FE simulation and experimental test are shown in Figure 11.
Figure 12 illustrates the results of the maximum impact load, impulse, duration of the impact load, maximum mid span deflection, and the time taken for the maximum deflection obtained at each drop height of the beams. With increasing the drop height, the maximum impact load and the maximum mid span deflection increased. Results showed that with enhancing of drop height, the FE results get closer to the experimental results. For example, at drop height of 0.3 m, results of the impact force had more errors compared to impact force at 1.2 m height. Impact force has straight relationship to the absorbed energy and when impact load is intensive, the absorption energy is also high. Since the proposed FE method considers the inertia effects, energy absorption and strain rate effects, it has high ability in simulation of impact loading. According to the results, it is noticed that FE results have higher errors at low drop height and by increasing the height of impact, the error between experimental and FE results decreases. Crack propagation and crack index for the beam under the impact load of fallen ball from 0.3 m height is indicated in Figure 13.
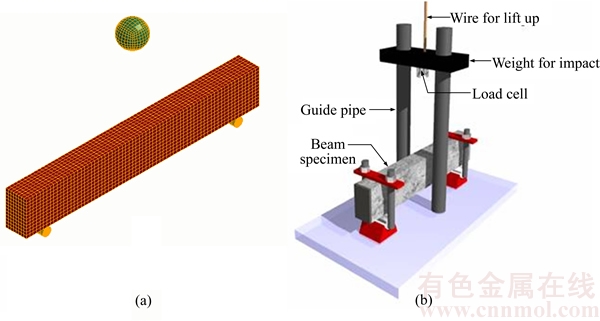
Figure 11 FE (a) and experimental conditions (b) [13] for impact test
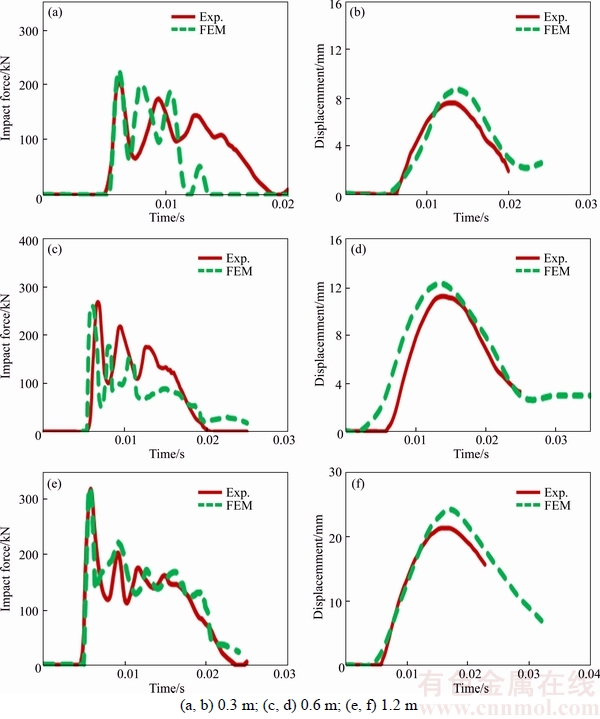
Figure 12 Impact response for specimen B3 at different drop heights
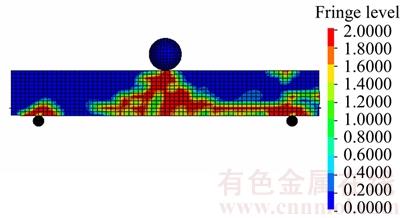
Figure 13 Crack propagation in beam with 0.3 m drop height after impact
4 Conclusions
1) With increase of loading rate, the total number of cracks decreased significantly.
2) The maximum strength and the area under the load–deflection curve also enhanced with the increase of loading rate.
3) Sometimes, the mode of failure changed from shear failure at the static rate to flexure failure at the high rate loads.
4) Standard sectional analysis with rate- dependent material properties does not accurately predict the behavior of beams under high rate loading. The reason is the localized yielding of rebars due to the enhanced bond properties at high rates.
5) The characteristics of impact loading such as the maximum impact load, the impulse, the duration of impact load, the maximum midspan deflection, and the time taken for the maximum mid-span deflection increased as the drop height increased.
6) The duration of impact load, the maximum mid span deflection, and the time taken for the maximum midspan deflection were affected by the flexural rigidity of the RC beams.
7) Overall, FE method had an reasonable ability for predicting the behavior of RC beam under various loading rates with different conditions. However, discrepancies were observed in the results due to homogeneity of the materials in modeling and the type of interaction.
References
[1] ZHAO H, GARY G. On the use of SHPB techniques to determine the dynamic behavior of materials in the range of small strains [J]. International Journal of Solids and Structures, 1996, 33: 3363–3375. DOI: 10.1016/0020- 7683(95)00186-7.
[2] LU Y, LI Q. Appraisal of pulse-shaping technique in Split Hopkinson pressure bar tests for brittle materials [J]. International Journal of Protective Structures, 2010, 23: 363–390. DOI: 10.1260/2041-4196.1.3.363.
[3] LI X, WANG S, WENG L, HUANG L, ZHOU T, ZHOU J. Damage constitutive model of different age concretes under impact load [J]. Journal of Central South University, 2015, 22: 693–700. DOI:10.1007/s11771-015-2572-0.
[4] FREW D J, FORRSTAL M J, CHEN W. Pulse shaping techniques for testing brittle materials with a split hopkinson pressure [J]. Bar Experimental Mechanics, 2002, 42: 93–106. DOI: 10.1007/BF02411056.
[5] YAN D, LIN G. Dynamic properties of concrete in direct tension [J]. Cement and Concrete Research, 2006, 36: 1371–1378. DOI: 10.1016/j.cemconres.2006.03.003.
[6] BISCHOFF P, PERY S. Compressive behaviour of concrete at high strain rates [J] Materials and Structures, 1991, 24: 425–450. DOI: 10.1007/BF02472016.
[7] KULKARNI S M, SHAH S P. Response of RC beams at high strain rates [J]. ACI Structural Journal, 1998, 95: 705– 715. https://www.scholars.northwestern.edu/en/ publications/ response-of-reinforced-concrete-beams-at-high-strain-rates.
[8] REMENNIKOV A, KAEWUNRUEN S. Impact resistance of RC columns: Experimental studies and design considerations [C]// 19th Australasian Conference on the Mechanics of Structures and Materidls. Christchurch, New Zealand: Tailor & Francis, 2007: 817–824.
[9] HUGHES G, SPEIRS D M, CEMENT A. Concrete, an investigation of the beam impact problem [M]. Wexham Springs, Slough: Cement and Concrete Association, 1982.
[10] WEERHEIJM J, VAN DOORMAAL J. Tensile failure of concrete at high loading rates: New test data on strength and fracture energy from instrumented spalling tests [J]. International Journal of Impact Engineering, 2007, 34: 609–626. DOI: 10.1016/j.ijimpeng.2006.01.005.
[11] TACHIBANA S, MASUYA H, NAKAMURA S. Performance based design of RC beams under impact [J]. Natural Hazards and Earth System Science, 2010, 10: 1069–1078. DOI: 10.5194/nhess-10-1069-2010.
[12] SAATCI S, VECCHIO F J. Effects of shear mechanisms on impact behavior of RC beams [J]. ACI Structural Journal, 2009, 106: 78–86. https://search.proquest.com/ openview/ cb6c52d186d6d9bb4700e846d5af20e4/1?pq-origsite=gscholar&cbl=36963.
[13] FUJIKAKE K, LI B, SOEUN S. Impact response of RC beam and its analytical evaluation [J]. Journal of Structural Engineering, 2009, 135: 938–950. https://ascelibrary.org/ doi/abs/10.1061/(ASCE)ST.1943-541X.0000039.
[14] ADHIKARY S D, LI B, FUJIKAKE K. Dynamic behavior of RC beams under varying rates of concentrated loading [J]. International Journal of Impact Engineering, 2012, 47: 24–38. DOI: 10.1016/j.ijimpeng.2012.02.001.
[15] XIAO S, CAO W, PAN H. Experiment of reinforced concrete beams at different loading rates [C]// 15th World Conference on Earthquake Engineering, 2012.
[16] GOLSTON M, REMENNIKOV A, ShEIKH M N. Experimental investigation of the behaviour of concrete beams reinforced with GFRP bars under static and impact loading [J]. Engineering Structures, 2016, 113: 220–232. DOI: 10.1016/j.engstruct.2016.01.044.
[17] QASRAWI Y, HEFFERNAN P J, FAM A. Dynamic behaviour of concrete filled FRP tubes subjected to impact loading [J]. Engineering Structures, 2015, 100: 212–225. DOI: 10.1016/j.engstruct.2015.06.012.
[18] HALLQUIST J O. LS-DYNA keyword user’s manual: Volume II material model [M]. Livermore Software Technology Corporation (LSTC), 2014.
[19] BRANNON R M, LEELAVANICHKUL S. Survey of four damage models for concrete [R]. Prod Sandia Gov, 2009: 1–80. DOI: 10.2172/993922.
[20] CRAWFORD J E, WU Y, CHOI H, MAGALLANES J M, LAN S. Use and validation of the release III K&C concrete material model in LS-DYNA [M]. Glendale: Karagozian Case, 2012.
[21] TU Z, LU Y. Evaluation of typical concrete material models used in hydrocodes for high dynamic response simulations [J]. International Journal of Impact Engineering, 2009, 36: 132–146. DOI: 10.1016/j.ijimpeng.2007.12.010.
[22] WU Y, CRAWFPRD J E, MAGALLANES J M. Performance of LS-DYNA concrete constitutive models [C]// 12th International LS-DYNA Users Conference, 2012.
[23] MALVAR J. Simplified concrete modeling with* Mat- Concrete-Damage-Rel3 [M]. 2005: 49–60. http:// roadsafellc.com/NCHRP22-24/Literature/Papers/SIMPLIFIED%20CONCRETE%20MODELING%20WITH%20MAT_CONCRET_DAMAGE_REL3.pdf.
[24] HANSSON P S H. Simulation of concrete penetration in 2D and 3D with the RHT material model [M]. Swedish Defense Research Agency, 2002.
[25] ZHENGUO T, YONG L. Evaluation of typical concrete material models used in hydrocodes for high dynamic response simulations [J]. International Journal of Impact Engineering, 2009, 36: 132–146. DOI: 10.1016/ j.ijimpeng.2007.12.010.
[26] COTSOVOS D, PAVLOVIC M. Numerical investigation of concrete subjected to high rates of uniaxial tensile loading [J]. International Journal of Impact Engineering, 2008, 35: 319–335. DOI: 10.1016/j.ijimpeng.2007.03.006.
[27] RIISGAARD B, NGO T, MENDIS P, GEORGAKIS C, STANG H. Dynamic increase factors for high performance concrete in compression using split Hopkinson pressure bar [C]// 6th International Conference on Fracture Mechanics of Concrete and Concrete Structures, 2007. https://scholar. google.com/scholar?hl=en&as_sdt=0%2C5&as_vis=1&q=Dynamic+increase+factors+for+high+performance+concrete+in+compression+using+split+hopkinson+pressure+bar&btnG=.
[28] ABBASNIA R, MOHAJERI F, RASHIDIAN O, USEFI N. Theoretical resistance of rc frames under the column removal scenario considering high strain rates [J]. Journal of Performance of Constructed Facilities (ASCE), 2016, 30(5). DOI: 10.1061/(ASCE)CF.1943-5509.0000867.
[29] ASPRONE D, FRASCADORE R, DI LUDOVICO M, PROTA A, MANFREDI G. Influence of strain rate on the seismic response of RC structures [J]. Engineering Structures, 2012, 35: 29–36. DOI: org/10.1016/j.engstruct.2011.10.025.
[30] CARTA G, STOCHINO F. Theoretical models to predict the flexural failure of RC beams under blast loads [J]. Engineering Structures, 2013, 49: 306–315. DOI: 10.1016/ j.engstruct.2012.11.008.
[31] MIN F, YAO Z, JIANG T. Experimental and numerical study on tensile strength of concrete under different strain rates [J]. The Scientific World Journal, 2014, 2014(11): 173531. DOI: 10.1155/2014/ 173531.
[32] MALVAR L J, ROSS C A. Review of strain rate effects for concrete in tension [J]. Materials Journal, 1998, 95: 735– 739. https://www.researchgate.net/publication/280015460_ A_Review_of_Strain_Rate_Effects_for_Concrete_in_TensionJ.
[33] MALVAR L J, CRAWFORD J E. Dynamic increase factors for steel reinforcing bars [M]. https://www.researchgate. net/publication/235099732_Dynamic_Increase_Factors_for_Steel_Reinforcing_Bars
[34] CEB-FIP Code 1990: Design code [M]. Thomas Telford, 1993.
[35] USEFI N, MOHAJERI F, ABBASNIA R. Finite Element analysis of RC elements in progressive collapse scenario [J]. Gradevinar, 2016, 68: 1009–1022. DOI: 10.14256/JCE.1550. 2016.
[36] MOHAJERI F, USEFI N, ABBASNIA R. Analytical investigation of reinforced concrete frames under middle column removal scenario [J]. Advances in Structural Engineering, 2017. https://doi.org/10.1177/1369433217746343.
[37] ABBASNIA R, MOHAJERI NAV F, USEFI N. A new method for progressive collapse analysis of RC frames [J]. Structural Engineering and Mechanics, 2016, 60(1): 31–50. DOI: 10.12989/sem.2016.60.1.031.
(Edited by YANG Hua)
中文导读
不同加载速率下钢筋混凝土梁的LS-DYNA数值研究
摘要:准确认识高应变率荷载作用下混凝土的受力性能以减少损伤的发生具有重要意义。由于实验研究的复杂性和较高的成本,数值研究是适合的方法。因此,本文采用LS-DYNA软件对有限元法在不同荷载作用下预测混凝土性能的能力进行评价。首先,给出该方法;然后,在不同条件下分3个阶段进行验证。荷载–跨中位移的计算结果表明,试验结果与有限元结果吻合较好。利用有限元方法对不同载荷作用下的梁进行分析,验证有限元方法在不同载荷下的受力分析能力。此外,该方法对不同加载速率、不同加载条件下钢筋混凝土梁的性能也具有较好的评价能力。
关键词:应变率;动态载荷;RC梁;冲击载荷;有限元;LS-DYN
Received date: 2017-03-20; Accepted date: 2017-04-13
Corresponding author: Leila MAJIDI, Master Graduate Student; Tel: +98–9127801200; E-mail: leilamajidi@alumni.iust.ac.ir

