基于二维广义Logistic映射和反馈输出的图像加密算法

涂立^{1, 2}，张弛²，张应征³，贾丽媛²

(1. 华中科技大学 计算机科学与技术学院，湖北 武汉，430074；

2. 湖南城市学院 信息科学与工程学院，湖南 益阳，413000；

3. 湖南工程职业技术学院 信息工程系，湖南 长沙，410004)

摘要：提出一个利用广义Logistic映射构造的二维非线性混沌映射，采用相图、分岔图分析方法，研究该混沌映射的非线性动态特性；利用该二维混沌方程生成混沌序列，将混沌序列进行优化改进，生成密钥序列；采用输出反馈的加密方式，改变图像的像素，达到加密的目的。实验仿真结果表明：该加密算法对明文和密文都非常敏感，混沌序列的选择极其敏感地依赖于明文，有效地提高了抵御选择明文攻击的能力；密文图像信息熵为7.974 3，接近理想值8.000 0，因而加密图像像素具有类随机均匀分布特性；加密图像和明文图像之间的相关性非常小，相邻像素具有零相关特性，而且密钥空间达到299 bit，加密方法大大改变了明文图像的像素，使得密文能够抵御统计攻击；本算法有很高的安全性，具有良好的加密效果。

关键词：虫口模型；图像加密；输出反馈

中图分类号：TP309.7          文献标志码：A         文章编号：1672-7207(2014)06-1893-07

A novel image encryption algorithm based on two-dimensional general Logostic mapping and output-feedback

TU Li^{1, 2}, ZHANG Chi², ZHANG Yingzheng³, JIA Liyuan²

(1. School of Computer Science and Technology, Huazhong University of Science and Technology, Wuhan 430074，China;

2. School of Information Science and Engineering, Hunan City University, Yiyang 413000, China;

3. Department of Information and Engineering, Hunan Engineering Polytechnic, Changsha 410004, China)

Abstract: A nonlinear coupled two-dimensional generalized Logistic chaotic mapping was proposed by using phase maps and bifurcation graphics, and the complex nonlinear dynamic activities of two-dimensional formula were studied. By using the coupled two-dimensional generalized Logistic chaotic mapping a chaotic sequence was generated, then the chaotic sequence was optimized into secret key stream, and output-feedback technology was introduced in this encryption algorithm, which changes pixels. The results show that the encryption algorithm is extremely sensitive to the key and the encrypted image, the choice of chaotic sequence sensitively depends on the plaintext that enhances the ability of resisting the chosen plaintext attack, and the information entropy of the cipher image is 7.974 3, which is very close to the ideal value 8.000 0. The encrypted image has random-like distribution behavior of grey values, and the correlation between the encrypted image and the plain image is close to 0. The adjacent pixels have zero co-correlat ion properties, and the encryption method changes the pixel of the original image greatly, which makes the ciphertext resist statistical attack, and the algorithm has the advantages of large space, and the key space reaches 299 bit.

Key words: insect population model; image encryption; output-feedback

随着计算机网络和信息技术的迅猛发展，多媒体通信已经成为人们信息交流的主要方式之一。数字图像具有数据量大、相关度高等特点，是多媒体信息中一种重要的信息表达形式，已经在人们的生活中得到广泛应用^[1-2]。但是，数字图像的传输存在着很多安全隐患，信息安全已成为日益严峻的现实问题，因此，研究图像加密具有重要的现实意义。数字图像安全性特别重视保密性、完整性、鉴别性和不可抵赖性。加密图像最直接的方法是使用经典的加密算法如AES(anvanced encryption standard)对图像文件进行加密。但是，由于图像与文本具有不同特性，这种方法并不能完全保证图像的安全性。由于数字图像的自身特点，用传统的密码学来对图像进行加密却不太合适，效果一般，而且效率不高。混沌和密码学之间有着天然的相似性，混沌系统是高度的非线性系统，具有伪随机性、遍历性且对初值极度敏感，很多混沌系统与密码学常用的Feistel网络结构非常相似，混沌系统本身是非线性确定性系统, 因而方便于保密通信系统的构造与研究。近年来，国内学者对混沌图像加密的研究取得了不少成果。朱从旭等^[3]提出了基于超混沌系统和密文交错扩散的图像加密新算法，周庆等^[4]提出了基于混沌映射并行算法的加密方法等。以往用于图像加密的混沌系统有基于像素位置加密的Arnold变换加密方法^[5]，还有一维的Logistic映射^[6]、二维的Henon 映射^[7-9]、三维的Lorenz 映射^[10]。在这些常用的混沌加密算法中，低维混沌系统存在密钥空间小、安全性不高的缺点^[11]。有的混沌系统甚至还会像低维混沌系统一样出现“稳定窗”^[12]和“空白窗”，大大降低了加密算法的加密效果。尽管以上图像加密方法得到了广泛应用，但在安全性方面还有待进一步提高，为此，本文作者将混沌理论引入到图像加密等信息安全领域。

1  混沌映射

混沌可以看成是一种无周期的有序，是自然界中客观存在的有界的、不规则的、复杂的运动形式。1963年，Lorenz发现了著名的Lorenz吸引子，提出了著名的蝴蝶效应(butterfly effect)^[13]，并由此推断出长期的天气预报不可预测。这是指在一个确定的动力系统中，初始条件的极小偏差将会引起结果的极大差异。这种现象说明系统的结果对初始条件具有极为敏感的依赖性，包括如下特征：

(1) 有界性。系统的运动轨道局限在一个有限的区域之内，系统从整体上来说是稳定的。

(2) 内随机性。混沌貌似噪声，但不同于噪声，由完全确定的方程描述，无需附加任何随机因数，系统都会表现出类似随机性的行为。

(3) 分形性。Lorenz吸引子具有分形的结构。

(4) 遍历性。在混沌吸引域内，混沌运动是各态经历的，在有限的时间内，混沌轨道会经历混沌区间里面的每一个点。

(5) 混沌现象还具有对初始条件的敏感依赖性。只要初始条件稍有偏差或有微小扰动，会使得系统的最终状态出现巨大的差异。因此，混沌系统的长期演化行为是不可预测的。

Matthews 最早将离散混沌动力系统应用于加密算法^[14]；Fridrich提出基于混沌的图像加密思想^[15]。混沌的特点使得它在密码学的应用上具有天然优势。

1.1  Logistic映射

Logistic方程又叫虫口模型。Logistic方程用于分析昆虫种群的个体数量与环境因素的关系，它是一个十分简单但又具有重要意义的一维非线性方程，其表达式为

            (1)

其中：x_k∈(0,1)；k=0，1，2，…，n；μ∈(0,4]，为分支参数。图1所示为Logistic映射的分岔图。

图1  Logistic映射分岔图

Fig. 1  Iterative result diagram for logistic map

从图1可以看出：当μ=3时，单线开始分岔为2个周期；在μ=1+处，开始出现4个周期；在此之后，大量的倍周期分支出现在越来越窄的μ间隔里，经过n次分支，周期长度为2n。这种周期倍化的过程没有限制，但相应的μ有1个极限值：3.569 945 67…；当3.569 945 67＜μ≤4.000 000 00时便进入混沌区间。

1.2  广义Logistic映射

在一维非线性Logistic映射的基础上，提出广义Logistic映射的概念。广义Logistic映射可以描述为

 (2)

首先研究参数μ 的变化范围。因为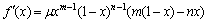，f′(x)在区间[0,1]内仅存在1个零点，故f(x)在该区间内为单峰函数，且峰值为最大值。

令，在迭代过程中，应保证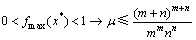，迭代的不动点方程为x^*=f(x^*)→μ(x^*)^m-1(1-x^*)ⁿ，而不动点处临界稳定条件为f ′(x*)=1，联立上式，给出μ 的下限为

；

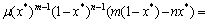
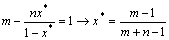从而 。

μ 的取值变化范围为

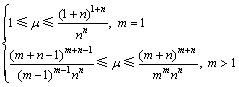    (3)

广义Logistic映射的参数m可以由式(3)确定，但具体的广义Logistic映射的混沌性质还需要具体研究。

2  二维广义Logistic混沌映射

利用广义Logistic映射构建一个有耦合项的二维方程，方程如下：

       (4)

该方程的动力学行为由参数μ₁，μ₂，γ₁，γ₂以及初始值x₀和y₀控制，从映射的形式上看，该映射可看作2个广义Logistic映射在二维情况下的推广，x_i和y_i可以看作2个不同的种群。其中：μ₁和μ₂为种群相应的环境参数；γ₁和γ₂可以看成是2个种群的制约系数。这2个种群既有各自的发展规律，又互相依存，互相制约。

由此可以预测当μ₁和μ₂取适当值时，可能出现周期分岔。为了对系统进行全面分析，有选择性地分析以下几组数据，研究系统的演化过程：取初值x₀=0.4，y₀=0.41和γ=0.1，参数μ₁=μ₂在区间(0,1.8)之间变化，计算x_k和y_k的迭代值，从迭代值可以得出相关的分岔图，见图2。

图2  参数μ控制下的x和y的分岔图

Fig. 2  Iterative results diagram for map x and y

从图2可以看出：x_k和y_k的迭代值都与参数μ有关，在μ∈(0,0.9)区间，它们都会收敛到1个固定值，叫不动点；当μ在区间(1.0,1.2)时，x_k和y_k都变成2个分支；当μ继续增大时，x_k和y_k各自发生倍周期分岔，进入混沌状态，它们在μ₁∈(1.3,1.6)区间，会有一个比较稳定的混沌区间；当μ＞1.6时，x_k和y_k都变得不可控。x_k和y_k都以倍周期分岔的方式走向混沌。

在参数γ不变的情况下，改变迭代值x₀和y₀，从0.1~0.8，迭代产生的分叉图形状不变。保持初值x₁=0.2和y₁=0.21不变，取μ₁=0.9，μ₂=0.7，参数γ₁=γ₂在区间(0，0.7)之间变化，得到图3所示x_k和y_k分岔图像。从图3可见：与图2(a)和图2(b)相比，分岔的形状已经大大改变，并且混沌区间也发生了很大改变；当μ₁＞0.7时，x_k和y_k都变得不可控。

图3  参数γ控制下的x和y的分岔图

Fig. 3  Iterative results diagram for map x and map y

从图2和图3可以看出：取不同的参数值进行迭代计算，系统将获得不同的混沌区间。

3  加密和解密方法

3.1  加密过程

先利用二维方程生成混沌序列，由于原始的混沌序列是实数型序列，与图像的整数型像素不匹配，因此，在对图像加密之前，必须对混沌序列进行优化，生成密钥序列，具体加密算法步骤如下。

Step 1：利用二维方程进行迭代计算。为了保证计算结果的混沌特性，将前N₀次的迭代计算结果弃用，从第N₀+1次迭代结果开始取值，生成2个一维序列x和y，序列的长度都是m×n，对应原始图像的像素点个数。

Step 2：将x序列进行归一化处理：分别求出x序列的最大值x_max和最小值x_min，利用(x_i-x_min)/(x_max-x_min)进行计算，使x序列转换成值域为(0,1)之间的混沌序列；对y序列也进行同样处理，使y序列归一化。

Step 3：将x序列小数点后的第3，7和6位取出，组成1个3位数，然后将该3位数对256进行求余运算，这样实数序列x被改造成整数序列；

Step 4：将改造成整数后的x序列转换成二维数组x₁(m，n)，按照同样的方法，将y序列归一、取整处理后，转换成二维数组y₁(m，n)，生成的x₁(m，n)和y₁(m，n)系列既是加密的密钥，也是待用的解密密钥。

Step 5：原始图像的像素值矩阵是A(m，n)，对明文图像进行行加密，行加密分2步进行。

(a) 对明文图像的第1行采用以下方式加密：

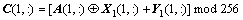
(b) 对于明文图像的其他行i(i＞1)的像素，加密的效果与明文A(i,:)、密钥序列元素X₁(i,:)和Y₁(i,:)以及密文序列元素C(i,:)有关，即采用加密反馈方法对明文图像进行加密，加密公式如下：

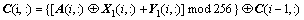
Step 6：对已经行加密后的序列进行第2轮加密，即列加密，列加密也分2步进行。

(a) 对明文图像的第1列采用以下方式加密：

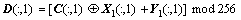
(b) 对明文图像的第1行采用以下方式加密：

Step 7：D(m，n)即为加密后的密文图像的像素矩阵。

3.2  解密过程

解密过程是加密的逆操作过程。在解密过程中需要注意的是：先进行列解密，再进行行解密，而且每一轮行(列)的解密顺序应该是从末行(末列)开始。具体解密方法如下。

Step 1：先利用下列公式进行列解密。

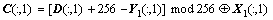
Step 2：再利用下列公式进行列解密。

B(m，n)就是解密后的图像。

4  仿真实验效果

在实验中使用256×256 的8位Elaine灰度图像，在Matlab7.1下进行仿真实验。系统参数采用：x₁=0.4，y₁=0.41，r₁=0.1，r₂=0.11，μ₁=1.5，μ₂=1.500 1。系统迭代计算的前1 000次结果弃用，即N₀=1 000，用http://sipi.usc.edu/database/提供的经典测试图像进行仿真，得到的原始图像和加密图像如图4所示。

图4  原始图像和加密图像

Fig. 4  Original image and encrypted image

5  算法分析

5.1  直方图分析

直方图代表灰度图像中像素的分布特性。图5所示为原始图像和密文图像所对应的像素分布直方图。从图5(a)可见：原始图像的像素分布是不均匀的，低像素的分布概率远远大于高像素的分布概率，而加密图像的像素在[0，255]范围内出现的概率几乎相等，即加密方法大大改变了原始图像的像素，使得密文能够抵御统计攻击。

5.2  相邻像素相关性分析

原始图像相邻像素之间具有很强的相关性, 加密的结果改变了原来相邻像素间的联系，即破坏了像素之间的相关性。若密图相邻像素之间的相关性变小,则说明密图安全性增强。原始图像和加密图像实际上都是离散的二维像素矩阵，这2个矩阵之间的二维相关系数C_AB定义为

    (5)

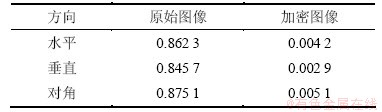
其中：A_ij和B_ij为明文、密文图像的像素矩阵中坐标(i，j)处的像素；A为明文图像的像素平均值；B为密文图像的像素平均值。采用前述初始参数对原始图像和加密图像进行测试，分别得到它们的密文图像和明文图像之间的相关性，结果如表1所示。

图5  原始图像的直方图和加密图像的直方图

Fig. 5  Histogram of original image and histogram of encrypted image

从表1可见：本文算法所得的加密图像和明文图像之间的相关性C_AB非常小，接近于0。

5.3  密钥敏感性分析

密钥敏感性是指在原来的解密密钥Key1基础上进行微小变化，得到Key2。若用Key2 也可以对加密图像进行解密，则说明加密算法对密钥的变化不敏感；反之，若无法解密，则说明加密算法对密钥的变化敏感，该算法是安全的。对图像进行加密和解密时，关键是产生相同的混沌序列。下面分别使用相同初值和不同初值产生混沌序列，对加密图像进行解密。

表1  原图和密图的相邻像素的相关性

Table 1  Correlation of adjacent pixels for original image and encrypted image

采用密钥x₁=0.4，y₁=0.41，γ₁=0.1，γ₂=0.11，μ₁=1.5，μ₂=1.500 1，N₀=1 000进行解密，可以得到如图6(a)所示的正确解密图像。然后，每次仅使解密密钥中的1个初始变量改变10^-10，即将参数x₁改变成x₁=0.4+10^-10，或者将参数γ₁改变成γ₁=0.1+10^-10等，用这些错误密钥进行解密，将得到如图6所示的错误解密图像。

为了度量解密图像和原始图像的差别，引入均方误差E_MS ，通过计算图像灰度值的均方误差来进一步分析初值的敏感性。灰度的均方误差E_MS为

      (6)

其中：P＝{P(i, j)}和D＝{D(i, j)}分别为原始图像及其解密图像的像素。

图6  解密图像

Fig. 6  Decrypted images

通过MATLAB计算图像灰度的均方误差可得表2。结合图6和表2可知：只有使用原加密时的混沌序列即用正确密钥对图像进行解密，才能对图像正确解密，还原图像，E_MS=0；而解密所使用的混沌序列初值与加密时混沌序列初值即使只相差10^-10，得到的E_MS更接近加密图的E_MS，也根本不能复原图像，无法进行解密。以上分析说明利用本算法生成的混沌序列对初值敏感，加密的图像具有很好的保密性。

表2  灰度均方差

Table 2  Mean square error of gray

5.4  密钥空间分析

密钥空间大是加密算法安全的前提条件，本文加密方法采用混沌方程的6个状态变量初值作为原始密钥，密钥为K=(x₀，y₀，μ₁，μ₂，γ₁，γ₂)。这些参数的初始值都用15位小数的双精度实数表示，因此，密钥空间可以达到(10¹⁵)⁶≈2²⁹⁹，相当于299 bit的密钥长度。若将预迭代次数N₀也作为原始密钥，则密钥空间更大。最基本、最流行攻击密图的方法是对密钥进行穷尽搜索，若采用穷举法，则对于16×16的图像运算次数为156!≈8.6×10⁵⁰⁶；对于256×256 的图像，运算次数为65 536!≈5.2×10^{287 193}。由于混沌系统具有较高的安全保密性能，密钥空间为实数，由此可见本算法的密钥空间非常大，能够有效地抵御对密钥的穷举攻击。

5.5  信息熵分析

信息熵是反映信息随机性的重要度量指标。设s代表一种信息源，则s的信息熵H(s)可以用下式进行计算：

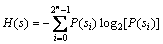         (7)

其中：P(s_i)表示像素s_i 出现的概率；2ⁿ为原始图像s像素的灰度等级。对1个能发出2ⁿ个符号的真随机信源，其信息熵就是n。以1幅 256 级灰度图像作为信息源为例，其像素有2⁸种可能值，因此，1幅256级灰度图像的理想信息熵应该是8。若1幅256级灰度图像的加密图像具有接近8 的信息熵，则表明该密文图像接近随机分布。对原始图像用本文算法加密，得到其密文图像信息熵为7.974 3，接近理想值8.000 0。这也说明加密图像具有良好的加密效果。

6  结论

(1) 首先提出广义Logistic映射，然后将广义Logistic映射该进程中带有耦合项的二维混沌方程，控制参数从2个增加到6个。该二维混沌方程的分岔和混沌区间受控制参数的控制，只要其中1个控制参数发生变化，系统的混沌区间也会随之发生变化，进而影响以后对图像加密的效果。

(2) 对该二维方程进行迭代计算生成混沌序列，这些混沌序列的随机性和分布均匀性比普通Logistic方程有显著提高。

(3) 本文提出的算法引进了输出反馈机制，进行行(列)加密时，第i行(列)的加密结果作为加密密钥应用到第i+1行(列)的加密过程中，第i+1行(列)的加密结果又被作为加密密钥应用到第i+2行(列)的加密过程中，因而第i行(列)的加密结果被直接或者间接地应用到后面的行(列)加密中，这样就使得前面的行(列)的加密效果扩散，进而影响了其余像素点的加密效果。该算法的特点是密钥空间大，可以抵抗差分攻击，也足够阻止各种穷举分析，加密效率高，相邻像素之间的相关性接近于0，而且密钥的敏感性非常高。本加密算法在图像加密和网络通信中有潜在的应用价值。

(4) 将本算法扩充，可以用于对彩色图片(RGB格式)进行加密。本加密算法还可以进一步改进，以便对像素位置和像素进行双重加密，进一步提高加密效率和算法复杂性。

参考文献：

[1] 张雪锋, 范九伦. 一种基于混沌系统的数字图像隐藏技[J]. 计算机工程, 2007, 33(4): 134-136.

ZHANG Xuefeng, FAN Jiulun. Digital image hiding technology based on chaos system[J]. Computer Engineering, 2007, 33(4): 134-136.

[2] FU Chong, CHEN Junjie, ZOU Hao, et al. A chaos-based digital image encryption scheme with an improved diffusion strategy[J]. Optics Express, 2012, 20(3): 2363-2378.

[3] 朱从旭, 胡玉平, 孙克辉. 基于超混沌系统和密文交错扩散的图像加密新算法[J]. 电子与信息学报, 2012, 34(7): 1735-1744.

ZHU Congxu, HU Yuping, SUN Kehui. New image encryption algorithm based on hyperchaotic system and ciphertext diffusion in crisscross pattern[J]. Journal of Electronics & Information Technology, 2012, 34(7): 1735-1744.

[4] 周庆, 胡月, 廖晓峰. 一个基于混沌映射的图像加密并行算法[J]. 计算机工程与应用, 2007, 43(22): 47-49, 66.

ZHOU Qing, HU Yue, LIAO Xiaofeng. Parallel image encryption algorithm based on chaos map[J]. Computer Engineering and Applications, 2007, 43(22): 47-49, 66.

[5] 孙克辉, 包善琴. 小波变换和子采样在彩色图像水印中的应用[J]. 中南大学学报(自然科学版), 2011, 42(2): 404-408.

SUN Kehui, BAO Shanqin. Application of wavelet transform and subsampling in color image watermark[J]. Journal of Central South University (Science and Technology), 2011, 42(2): 404-408.

[6] 邓绍江, 张岱固, 濮忠良. 一种基于复合混沌系统的数字图像加密算法[J]. 计算机应用研究, 2008, 25(10): 3097-3099.

DENG Shaojiang, ZHANG Daigu, PU Zhongliang. Digital image encryption algorithm based on composited discrete chaotic system[J]. Application Research of Computers, 2008, 25(10): 3097-3099.

[7] 郑凡, 田小建, 范文华, 等. 基于Henon映射的数字图像加密[J]. 北京邮电大学学报, 2008, 31(1): 66-70.

ZHENG Fan, TIAN Xiaojian, FAN Wenhua, et al. Image encryption based on henon map[J]. Journal of Beijing University of Posts and Telecommunications, 2008, 31(1): 66-70.

[8] 段文文, 李碧. 基于混沌的数字图像置乱算法及参数优化[J]. 计算机应用研究, 2011, 28(1): 329-331.

DUAN Wenwen, LI Bi. New digital image scrambling algorithm based on chaos and its parameters optimization[J]. Application Research of Computers, 2011, 28(1): 329-331.

[9] WU Yue, YANG Gelan, JIN Huixia, et al. Image encryption using the two-dimensional logistic chaotic map[J]. Journal of Electronic Imaging, 2012, 21(1): 013014-1.

[10] 卢辉斌, 刘海莺. 基于耦合混沌系统的彩色图像加密算法[J]. 计算机应用, 2010, 30(7): 1812-1817.

LU Huibin, LIU Haiying. Encryption algorithm of colour image based on coupling chaotic systems[J]. Journal of Computer Applications, 2010, 30(7): 1812-1817.

[11] ZHANG Huaguang, MA Tiedong, HUANG Guangbin, et al. Robust global exponential synchronization of uncertain chaotic delayed neural networks via dual-stage impulsive control[J]. IEEE Trans Syst Man Cybern B Cybern, 2010, 40(3): 831-844.

[12] 杨钒, 薛模根. 复合混沌二级置乱图像加密算法研究[J]. 合肥工业大学学报, 2009, 32(8): 1128-1131.

YANG Fan, XUE Mogen. Research on digital image encryption algorithm based on compound chaotic image second- scrambling[J]. Journal of Heifei University of Technology, 2009, 32(8): 1128-1131.

[13] LIU Hongjun, WANG Xingyuan. Color image encryption using spatial bit-level permutation and high-dimension chaotic system[J]. Opt Communications, 2011, 284(16/17): 3895-3903.

[14] May R M. Simple mathematical models with very complicated dynamics[J]. Nature, 1976, 261: 459-467.

[15] YANG Gelan, JIN Huixia, BAI Na. Image encryption using the chaotic Josephus Matrix[J]. Mathematical Problems in Engineering, 2014(3): 632060-632072.

(编辑  陈灿华)

收稿日期：2013-07-03；修回日期：2013-09-21

基金项目：国家自然科学基金资助项目(61374086)；湖南省科技计划项目(2013FJ3087，2012FJ4329)

通信作者：涂立(1974-)，男，湖南益阳人，副教授，从事混沌理论及数字图像处理研究；电话：0737-6353128；E-mail：tulip1903@163.com