J. Cent. South Univ. (2016) 23: 2917-2925
DOI: 10.1007/s11771-016-3355-y
Decentralized adaptive neural network sliding mode position/force control of constrained reconfigurable manipulators
LI Yuan-chun(李元春)1, 2, DING Gui-bin(丁贵彬)2, ZHAO Bo(赵博)3
1. Department of Control Science and Engineering, Changchun University of Technology, Changchun 130012, China;
2. Department of Control Science and Engineering, Jilin University, Changchun 130012, China;
3. State Key Laboratory of Management and Control for Complex Systems, Institute of Automation,Chinese Academy of Sciences, Beijing 100190, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: A decentralized adaptive neural network sliding mode position/force control scheme is proposed for constrained reconfigurable manipulators. Different from the decentralized control strategy in multi-manipulator cooperation, the proposed decentralized position/force control scheme can be applied to series constrained reconfigurable manipulators. By multiplying each row of Jacobian matrix in the dynamics by contact force vector, the converted joint torque is obtained. Furthermore, using desired information of other joints instead of their actual values, the dynamics can be represented as a set of interconnected subsystems by model decomposition technique. An adaptive neural network controller is introduced to approximate the unknown dynamics of subsystem. The interconnection and the whole error term are removed by employing an adaptive sliding mode term. And then, the Lyapunov stability theory guarantees the stability of the closed-loop system. Finally, two reconfigurable manipulators with different configurations are employed to show the effectiveness of the proposed decentralized position/force control scheme.
Key words: constrained reconfigurable manipulators; position/force control; model decomposition; decentralized control; neural network
1 Introduction
A reconfigurable manipulator consists of interchangeable links and joint modules in standard size and interfaces. These components can be easily assembled into various configurations to meet the requirements of diverse environments [1]. Therefore, compared with traditional manipulators with fixed structures, reconfigurable manipulators are more flexible, reliable and potential to be applied to many occasions, such as assembly industries, medical treatments, space explorations, home security or nuclear manipulations [2-8].
During the past several decades, the trajectory tracking problem of reconfigurable manipulators has attracted considerable attention worldwide. In Ref. [9], the authors have presented a motion planning method for the modular manipulator equipped with elementary motion primitives. The utilization of primitives significantly reduced the complexity of motion planning. Considering the model uncertainties caused by reconfiguration and uncompensated joint friction, the authors in Ref. [10] presented modular distributed control architecture for modular and reconfigurable manipulators (MRR) that can instantly adapt to different configurations. The parametric and non-parametric uncertainties were compensated by joint torque sensor measurement and robust controller, respectively. In Ref. [11], a novel design methodology of interval type-2 Takagi-Sugeno-Kang fuzzy logic controllers was proposed for reconfigurable manipulators with uncertain dynamic parameters. In Ref. [12], hierarchical search algorithm was designed for motion planning of multiple cooperating reconfigurable manipulators.
The strategies in above literatures are classified into centralized control and distributed one. However, decentralized control strategy is more suitable for reconfigurable manipulators which can change their configurations by adding or reducing modules to adapt different tasks. In Ref. [13], the authors presented a decentralized robust control algorithm for MRR based on Lyapunov stability analysis and backsteppping technique. In Ref. [14], the unknown dynamics and interconnection term were approximated by Takagi-Sugeno fuzzy logic system and adaptive sliding mode controller, respectively.To satisfy the current market demand, a multi-agent system based on decentralized control was proposed [15].
All the literatures mentioned above analyzed the case of free motion, i.e., reconfigurable manipulators without contacting with external environments. Actually, in many practical applications, such as polishing, grinding, deburring and assembling, the end-point of reconfigurable manipulator interacted with the environment inevitably. For these tasks, neither pure force control nor pure position control is sufficient and effective. Unfortunately, only a few efforts have been made on the decentralized position/force control of constrained reconfigurable manipulators at present. Moreover, in most of the previous literatures, the decentralized control strategies are used in multi- manipulator cooperation [16-21]. In these cases, each manipulator rather than a module is treated as a subsystem, which is not appropriate for application to decentralized position/ force control of series constrained reconfigurable manipulators. Different from traditional manipulators, to design decentralized position/force controller for constrained reconfigurable manipulators has two difficulties. One is model decomposition, namely how to use only local joint information to map the end-point contact force to each joint. Another is that the proposed controller should be used in different configurations without modifying any control parameters.
In this work, the decentralized position/force control problem of constrained reconfigurable manipulators is solved. In contrast to the previous decentralized position/ force controllers, the proposed control approach based on nonlinear feedback control strategy can achieve decentralized position/force control in series reconfigurable manipulators. The contact force is mapped to joint space via Jacobian matrix which includes the i-th joint’s real-time information and other joints’ desired information. Based on model decomposition technique, the dynamics can be represented as a set of interconnected subsystems. Owing to the excellent approximation capability for arbitrary linear or nonlinear functions through online learning, neither the precise dynamic model nor the dynamic linear parameterization is required to design the controller of each joint module. For each joint subsystem, only local information is used to approximate subsystem dynamic model through a neural network controller. Meanwhile, the related errors are compensated by a sliding mode controller.
2 Problem formulation
The dynamic model of n-DOF reconfigurable manipulator in joint space is expressed by
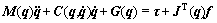 (1)
(1)
where 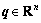 is the vector of joint displacements, M(q) is the symmetric and positive definite inertia matrix,
is the vector of joint displacements, M(q) is the symmetric and positive definite inertia matrix, 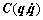 is the matrix of centripetal Coriolis matrix, G(q) is the gravity vector,
is the matrix of centripetal Coriolis matrix, G(q) is the gravity vector, 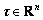 is the vector of generalized torque vector applied to each joint,
is the vector of generalized torque vector applied to each joint, 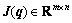 is the Jacobian matrix, and
is the Jacobian matrix, and 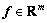 is the contact force vector in workspace coordinate. By considering each joint module as a subsystem, the dynamics of module i can be expressed as
is the contact force vector in workspace coordinate. By considering each joint module as a subsystem, the dynamics of module i can be expressed as
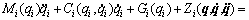
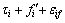 (2)
(2)
where
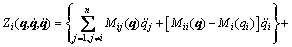
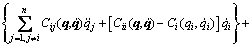
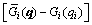 (3)
(3)
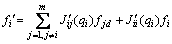 (4)
(4)
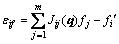 (5)
(5)
where 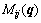 ,
, 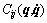 and
and 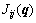 are the ij-th element of M(q),
are the ij-th element of M(q), 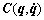 and JT(q), respectively; qi, fi,
and JT(q), respectively; qi, fi, 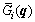 and τi are the i-th element of q, f, G(q) and τ, respectively; qid is the desired trajectory of i-th joint module;
and τi are the i-th element of q, f, G(q) and τ, respectively; qid is the desired trajectory of i-th joint module; 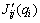 is the ij-th element of JT(q) which only contains the i-th joint module’s real-time value and other joint modules’ desired information, i.e.,
is the ij-th element of JT(q) which only contains the i-th joint module’s real-time value and other joint modules’ desired information, i.e., 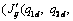
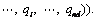
Some properties of the system model are addressed.
Property 1: Mi(qi) is an uniformly and bounded symmetric positive-definite scalar function, i.e.,
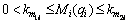 (6)
(6)
where m1i and m2i are unknown positive constants.
Property 2: 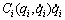 , Gi(qi) are all bounded as
, Gi(qi) are all bounded as 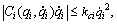
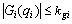 for kci>0, kgi>0, respectively.
for kci>0, kgi>0, respectively.
Property 3: Mi(qi) and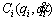 are scalar functions such that the following equation holds:
are scalar functions such that the following equation holds:
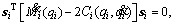
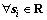 (7)
(7)
The control objective is to design a decentralized position/force control scheme for Eq. (2) to make the actual position q and force f of the reconfigurable manipulator follow their desired trajectories.
3 Controller design and stability analysis
3.1 Decentralized adaptive neural network sliding mode position/force controller design
Define the joint tracking error ei, the converted desired torque 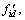 the converted torque error eif and the sliding mode surface si as
the converted torque error eif and the sliding mode surface si as
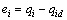 (8)
(8)
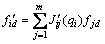 (9)
(9)
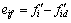 (10)
(10)
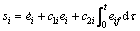 (11)
(11)
where c1i and c2i are positive constants, 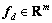 is the desired force of the end-point, and fjd is the j-th element of fd.
is the desired force of the end-point, and fjd is the j-th element of fd.
Assumption 1: Desired trajectories qid, 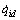 and
and 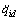 are bounded [22].
are bounded [22].
Assumption 2: The derivative of converted torque error 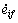 is uniformly continuous [23].
is uniformly continuous [23].
Combined by Eq. (8), Eq. (11) becomes
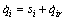 (12)
(12)
where 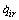 is defined as
is defined as
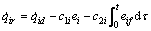 (13)
(13)
Combined with Eq. (8), the derivative of si can be expressed as
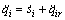 (14)
(14)
where 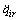 is defined as
is defined as
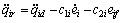 (15)
(15)
By substituting Eqs. (12) and (14) into Eq. (2), the dynamic equation of reconfigurable manipulator can be written as

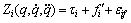 (16)
(16)
Then, Eq. (16) can be expressed as
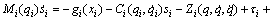
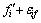 (17)
(17)
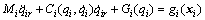 (18)
(18)
where 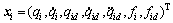 .
.
Assumption 3: The interconnection term 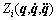 is bounded by [24]
is bounded by [24]
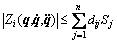 (19)
(19)
where 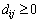 and
and 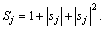
Actually, it is impractical to obtain the precise dynamic model of reconfigurable manipulator, that is to say, the nonlinear function gi(xi) and constant dij are all unknown. Meanwhile, reconfigurable manipulator usually configures various configurations to adapt to environments and task. In this case, to establish each dynamic model is not reasonable. In the following, an adaptive neural network sliding mode controller will be presented for each subsystem, which does not require the precise dynamic model. Figure 1 shows the block diagram of the controller. The proposed controller consists of two parts: a neural network controller and a sliding mode controller. The neural network controller represents the subsystem dynamics expressed in terms of the sliding variable. In the second part, the sliding mode controller is designed to compensate the interconnection and error which includes neural network approximation error, the converted torque error and error caused by the replacement in Jacobian matrix.
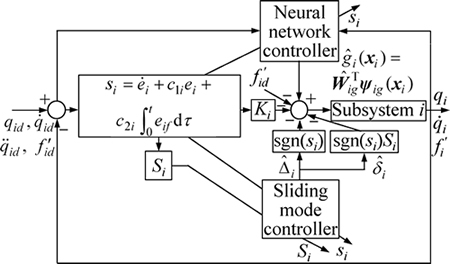
Fig. 1 Block diagram of subsystem i
According to the Properties 1-2 and Assumption 1, it is easy to draw the conclusion that the nonlinear term gi(xi) in Eq. (18) is bounded. Because of the ability to approximate the nonlinear function, the nonlinear term can be approximated by the neural network with appropriate dimension as
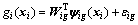 (20)
(20)
where Wig is the optimal parameter vector as Eq. (21), 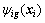 is the radial basis function and
is the radial basis function and 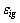 stands for the approximation error.
stands for the approximation error.
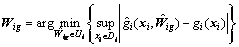 (21)
(21)
In Eq. (21), Ui and 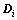 denote the sets of suitable bounds on
denote the sets of suitable bounds on 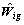 and xi, respectively.
and xi, respectively. 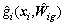 is the estimation of gi(xi), which can be represented as
is the estimation of gi(xi), which can be represented as
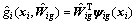 (22)
(22)
where 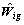 is an adjustable weight parameter vector. The estimate error
is an adjustable weight parameter vector. The estimate error 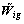 can be defined as
can be defined as
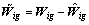 (23)
(23)
Define ωi as the sum of norm of the converted torque error eif, neural network approximate error εig and replacement error εif, thus
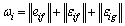 (24)
(24)
Assumption 4: The whole error ωi is bounded, i.e. ωi≤△i, where △i is an unknown positive constant.
The decentralized position/force control law is designed as
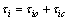 (25)
(25)
where
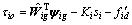 (26)
(26)
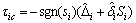 (27)
(27)
where Ki is a positive constant and δi is determined by interconnection term of each subsystem which can be expressed as
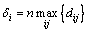 (28)
(28)
And define 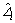 and
and 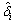 are estimations of Δi and δi.
are estimations of Δi and δi.
The estimation errors 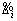 and
and 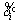 is defined as
is defined as
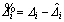 (29)
(29)
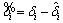 (30)
(30)
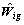 ,
, 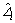 and
and 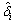 are updated by the following adaptive laws:
are updated by the following adaptive laws:
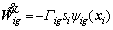 (31)
(31)
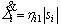 (32)
(32)
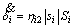 (33)
(33)
where 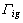 ,
, 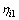 and
and 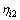 are positive constants.
are positive constants.
3.2 Stability analysis
Theorem: Consider subsystem dynamic model of constrained reconfigurable manipulators as Eqs. (2)-(5) with Assumptions 1-4. If the decentralized position/force controller is designed as Eqs. (25)-(27) with the adaptive laws Eqs. (31)-(33), the system position tracking error and force tracking error will converge to zero asymptotically.
Proof: Consider the Lyapunov function candidate
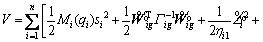
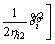 (34)
(34)
Differentiating V with respect to time, and substituting (17) into it, it yields
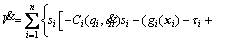
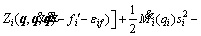
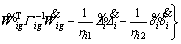 (35)
(35)
According to the Property 3, substituting Eq. (20) into Eq. (35) yields
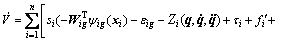
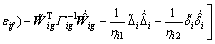 (36)
(36)
Substituting Eq. (26) into Eq. (36) yields
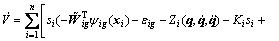
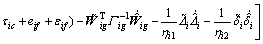 (37)
(37)
From Assumption 3 and Eq. (24), Eq. (37) can be expressed as
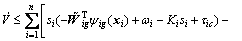
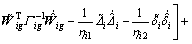
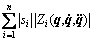 (38)
(38)
Using Chebyshev inequality, Eq. (38) can be computed as
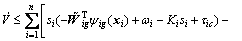
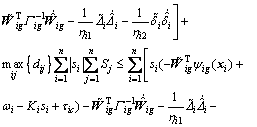
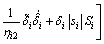 (39)
(39)
According to the Assumption 4, then Eq. (39) can be rewritten as
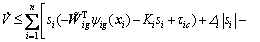
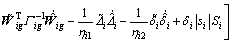 (40)
(40)
Substituting Eq. (27) into Eq. (40) yields
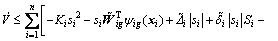
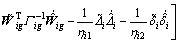 (41)
(41)
Then substituting Eqs. (31)-(33) into Eq. (41) yields
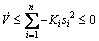 (42)
(42)
So, the solutions si, 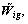
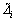 and
and 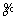 are all bounded. Using Eq. (17) and Eqs. (25)-(27), it is obviously known that
are all bounded. Using Eq. (17) and Eqs. (25)-(27), it is obviously known that 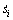 is bounded. Since the Lyapunov function candidate V is positive definite, and integral
is bounded. Since the Lyapunov function candidate V is positive definite, and integral 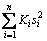 from 0 to t:
from 0 to t:
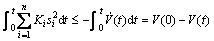 (43)
(43)
Because V(0) is bounded, V(t) is bounded and non-increasing, i.e.,
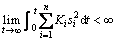 (44)
(44)
This implies that 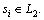 So, according to Barbalat Lemma, it is concluded that
So, according to Barbalat Lemma, it is concluded that 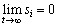 . Furthermore,
. Furthermore,
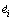 ,
, 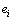 and eif are linearly independent, so the position tracking error ei and converted torque tracking error eif will also converge to zero asymptotically. On the other hand, using Assumption 2, if
and eif are linearly independent, so the position tracking error ei and converted torque tracking error eif will also converge to zero asymptotically. On the other hand, using Assumption 2, if 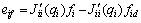 approaches zero, the force tracking error (f-fd) will also approach to zero [23, 25].
approaches zero, the force tracking error (f-fd) will also approach to zero [23, 25].
4 Simulations
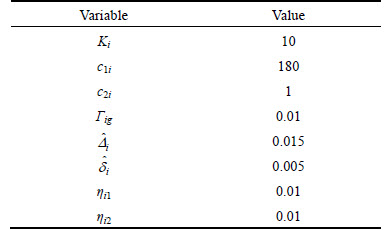
In order to verify the effectiveness of proposed decentralized control scheme, two 2-DOF (degree of freedom) reconfigurable manipulators with different configurations, whose dynamic models are same as those in Ref. [14], are employed for simulation. Suppose that the end-point is perpendicular to the contact surface and there is no Coulomb friction between them. Some related control parameters are listed in Table 1.
A three-layer neural network with seven neurons in
Table 1 Controller parameters
the hidden layer is created. Gaussian basis function is selected as
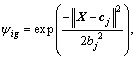 j=1, 2, …, m (45)
j=1, 2, …, m (45)
where cj and bj are the neural network center and width, respectively. Meanwhile, the initial values of weight vectors are chosen as 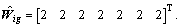
For configuration a, the desired trajectories are q1d=0.5cost+0.2sin(3t) and q2d=-0.5sint+0.6cos(3t). The initial positions are ones, and initial velocities are zeros.
The position and velocity tracking trajectories are illustrated in Fig. 2, where we can see that the tracking errors appear at the beginning of the simulation due to the lack of the knowledge about the dynamic model of subsystem. Then, the actual and the desired trajectories are almost coincident a few seconds later, and the position error curves are intuitively shown in Fig. 3.
The performance of the end-point actual force following the reference force is depicted in Fig. 4. The desired force is set to be fd=10N. Note that the dotted line tracks the solid line in a short time and the force tracking is generally satisfied.
The converted torque tracking errors of two joints are shown in Fig. 5. This means that the converted torque tracking errors can also converge to zero by mapping the end-point contact force to joint space. All these figures manifest that the control laws ensure the tracking performance of the position and contact force of configuration a.
To further test the effectiveness of the proposed control scheme under different configurations, the control laws are also applied to configuration b, whose desired trajectories are q1d=0.2sin(3t)+0.1cos(4t) and q2d=0.3sin(2t)+0.2cos(t).
The initial positions of joints are ones, and initial velocities are zeros. The parameters of the decentralized position/force controller are all chosen the same as those in configuration a. The trajectory tracking, force tracking and converted torque tracking errors of configuration b are shown in Figs. 6-9, respectively.
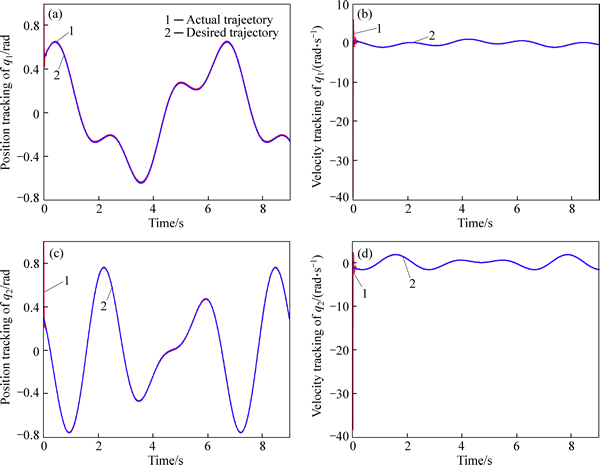
Fig. 2 Tracking performance of configuration a
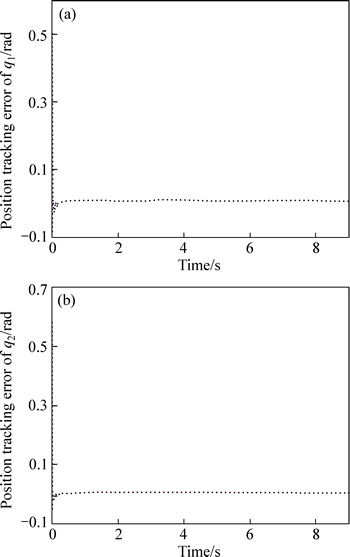
Fig. 3 Position tracking error of configuration a
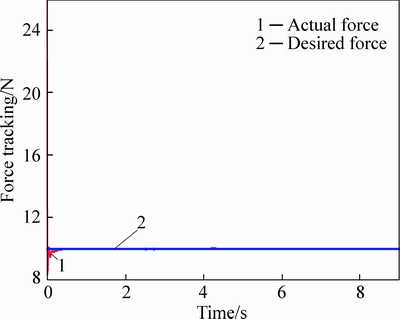
Fig. 4 Force tracking performance of configuration a
The simulation results demonstrate that the proposed decentralized position/force control strategy is applicable to different configurations without changing any control parameter. This is a solution for the difficulty of transforming the configuration to others to fulfill the variety of tasks in different environments. It is worth mentioning that the control strategy can also be applied to reconfigurable manipulators with more DOFs [26].
Fig. 5 Converted torque tracking error of configuration a
Fig. 6 Tracking performance of configuration b
Fig. 7 Position tracking error of configuration b
Fig. 8 Force tracking performance of configuration b
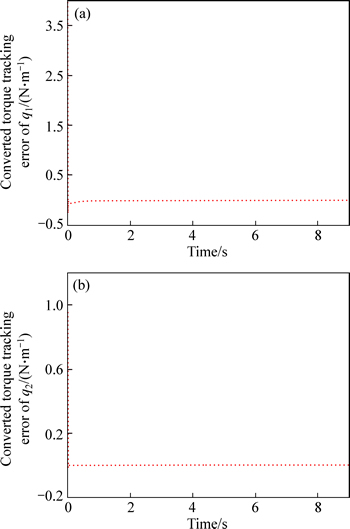
Fig. 9 Converted torque tracking error of configuration b
5 Conclusions
1) Because of the modularity property of constrained reconfigurable manipulators, the decentralized control scheme suits its control better. Conventional methods could not be directly used to be combined with decentralized position/force control strategy. Based on previous work, a novel model decomposition method has been introduced.
2) A decentralized adaptive neural network sliding mode position/force control scheme is presented for constrained reconfigurable manipulators. Theoretical analysis based on Lyapunov stability theory shows that the decentralized position/force controller can guarantee that both the position tracking error and the force tracking error converge to zero asymptotically.
3) Two 2-DOF reconfigurable manipulators are presented to show the effectiveness of the proposed control scheme. Simulation results show that the control strategy is feasible for different configurations of reconfigurable manipulators without modifying controller parameters.
References
[1] CHEN I M, YEO S H, CHEN G. Kernal for modular robot applications-automatic modeling techniques [J]. International Journal of Robotics Research, 1999, 18(2): 225-242.
[2] YOO S S, RAMA S, SZEWCZYK B, PUI J W Y, LEE W, KIM L. Endoscopic capsule robots using reconfigurable modular assembly: A pilot study [J]. International Journal of Imaging System and Technology, 2014, 24(4): 359-365.
[3] YIM M, SHEN W M, SALEMI B, RUS D, MOLL M, LIPSON H, KLAVINS E, CHIRIKJIAN G S. Modular self-reconfigurable robot systems: challenges and opportunities for the future [J]. IEEE Robotic Automation Magazine, 2007, 14(1): 43-52.
[4] HARADA K, OETOMO D, SUSILO E, MENCIASSI A, DANEY D, MERLET J P, DARIO P. A reconfigurable modular robotic endoluminal surgical system: vision and preliminary results [J]. Robotica, 2010, 28(2): 171-183.
[5] QIAO Gui-fang, SONG Guang-ming, WANG Ya-li, ZHANG Jun, WANG Wei-guo. Autonomous network repairing of a home security system using modular self-reconfigurable robots [J]. IEEE Transactions on Consumer Electronics, 2013, 59(3): 562-570.
[6] RUSSO S, HARADA K, RANZANI T, MANFREDI L, STEFANINI C, MENCIASSI A, DARIO P. Design of a robotic module for autonomous exploration and multimode locomotion [J]. IEEE/ASME Transactions on Mechatronics, 2013, 18(6): 1757-1766.
[7] ROEHR T M, CORDES F, KIRCHNER F. Reconfigurable integrated multi-robot exploration system: Heterogeneous modular reconfigurable robots for space exploration [J]. Journal of Field Robotics, 2014, 31(1): 3-34.
[8] DAS A N, MURTHY R, POPA D O, STEPHANOU H E. A multiscale assembly and packing system for manufacturing of complex micro-nano devices [J]. IEEE Transactions on Automation Science and Engineering, 2012, 9(1): 160-170.
[9] VONASEK V, SASKA M, WINKLER L, PREUCIL L. High-level motion planning for CPG-driven modular robots [J]. Robotics and Autonomous Systems, 2015, 68(10): 116-128.
[10] LIU Guang-jun, ABDUL S, GOLDENBERG A A. Distributed control of modular and reconfigurable robot with torque sensing [J]. Robotica, 2008, 26(1): 75-84.
[11] BIGLARBEGIAN M, MELEK WW, MENDEL J M. Design of novel interval type-2 fuzzy controllers for modular and reconfigurable robots: theory and experiments [J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1371-1384.
[12] KASPRZAK W, SZYNKIEWICZ W, ZLATANOV D, ZIELINSKA T. A hierarchical CSP search for path planning of cooperating self-reconfigurable mobile fixtures [J]. Engineering Applications of Artificial Intelligence, 2014, 34(9): 85-98.
[13] LI Z, MELEK W W, CLARK C. Decentralized robust control of robot manipulators with harmonic drive transmission and application to modular and reconfigurable serial arms [J]. Robotica, 2009, 27(2): 291-302.
[14] ZHU Ming-chao, LI Yuan-chun. Decentralized adaptive fuzzy sliding mode control for reconfigurable modular manipulators [J]. International Journal of Robust and Nonlinear Control, 2010, 20(4): 472-488.
[15] LEITAO P, BARBOSA J, TRENTESAUX D. Bio-inspired multi- agent systems for reconfigurable manufacturing systems [J]. Engineering Applications of Artificial Intelligence, 2012, 25(5): 934- 944.
[16] GARCIA-RODRIGUEZ R, PARRA-VEGA V. Decentralized sliding force/position PD control of cooperative robots in operational space under Jacobian uncertainty [C]// IEEE/RSJ International Conference on Intelligent Robots and Systems. Edmonton, Canada, 2005: 3200-3206.
[17] GUEAIEB W, KARRAY F, AL-SHARHAN S. A robust hybrid intelligent position/force control scheme for cooperative manipulators [J]. IEEE/ASME Transactions on Mechatronics, 2007, 12(2): 109-125.
[18] SADATI N, GHAFFARKHAH A. Decentralized position and force control of nonredundant multi-manipulator systems [C]// International Conference on Control, Automation and Systems. Seoul, Korea, 2007: 2223-2229.
[19] HARUHISA K, SATOSHI U, SATOSHI I. Decentralized adaptive coordinated control of multiple robot arms without using a force sensor [J]. Automatica, 2006, 42(3): 481-488.
[20] REZAEE H, ABDOLLAHI F. A decentralized cooperative control scheme with obstacle avoidance for a team of mobile robots [J]. IEEE Transactions on Industrial Electronics, 2014, 61(1): 347-354.
[21] WAIL G, FAKHREDDINE K, SALAH A. A robust hybrid intelligent position/force control scheme for cooperative manipulators [J]. IEEE/ASME Transactions on Mechatronics, 2007, 12(2): 109-125.
[22] ZHAO Bo, LI Yuan-chun. Local joint information based active fault tolerant control for reconfigurable manipulator [J]. Nonlinear Dynamics, 2014, 77(3): 859-876.
[23] GRABBE M T, BRIDGES M M. Comments on “force/motion control of constrained robots using sliding mode” [J]. IEEE Transactions on Automatic Control, 1994, 39(1): 179.
[24] ZHAO Bo, LI Yuan-chun. Signal reconstruction based active decentralized fault tolerant control for reconfigurable manipulators [J]. Acta Automatica Sinica, 2014, 40(9): 1942-1950. (in Chinese)
[25] SU Chun-yi, LEUNG T P, ZHOU Qi-jie. Force/motion control of constrained robots using sliding mode [J]. IEEE Transactions on Automation Control, 1992, 37(5): 668-672.
[26] DU Yan-li, LI Yuan-chun. Decentralized active fault-tolerant control for reconfigurable manipulator with simultaneous faults [J]. Journal of Central South University (Science and Technology), 2014, 45(3): 727-733. (in Chinese)
(Edited by YANG Bing)
Foundation item: Project(61374051, 61603387) supported by the National Natural Science Foundation of China; Projects(20150520112JH, 20160414033GH) supported by the Scientific and Technological Development Plan in Jilin Province of China; Project(20150102) supported by Opening Funding of State Key Laboratory of Management and Control for Complex Systems, China
Received date: 2015-09-09; Accepted date: 2015-12-30
Corresponding author: ZHAO Bo, PhD; Tel: +86-13843022689; E-mail: zhaobo@ia.ac.cn