文章编号:1004-0609(2012)1-0239-12
隐伏矿体立体预测的体元模型及其磁法正演模型
樊俊昌1, 2, 3,毛先成1, 2,赵 莹1, 2, 4,唐艳华1, 2,单文法1, 2,陈 进1, 2
(1. 中南大学 有色金属成矿预测教育部重点实验室,长沙 410083;
2. 中南大学 地球科学与信息物理学院,长沙 410083;
3. 山金西部地质矿产勘查有限公司,西宁 810016;
4. 湖南科技大学,湘潭 411201)
摘 要:针对隐伏矿体立体定量预测结果的可靠性问题,以及磁法正反演模型一直存在的地质依据不足和多解性问题,提出隐伏矿体立体预测体元模型与磁法正演模型在定量层面上相结合的新方法。利用体元模型的特点,结合磁荷面积分公式,推导出基于隐伏矿体立体预测体元模型的总磁场异常的数学模型,并进行算法设计和软件开发。以福建省尤溪县丁家山铅锌矿床为实例,计算得到研究区域的总磁场异常,绘制基于已知矿化体、预测矿化体及已知矿化体总体的理论总磁场异常等值线图,分别与实测等值线图进行比较分析。研究结果表明:以体元模型为纽带,可实现隐伏矿体立体定量预测结果与磁性体正演结果的耦合与互补,检验隐伏矿体立体定量预测结果的正确性,有效地降低隐伏矿体立体定量预测的风险。
关键词:隐伏矿体立体预测;体元模型;磁法正演模型
中图分类号:P612 文献标志码:A
Voxel model and its magnetic forward model of stereoscopic prediction of concealed ore body
FAN Jun-chang1, 2, 3, MAO Xian-cheng1, 2, ZHAO Ying1, 2, 4, TANG Yan-hua1, 2, SHAN Wen-fa1, 2, CHEN Jin1, 2
(1. Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Ministry of Education,
Central South University, Changsha 410083, China;
2. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;
3. Shanjin Western Geological and Mineral Exploration Co., Ltd., Xining 810016, China;
4. Hunan University of Science and Technology, Xiangtan 411201, China)
Abstract: Aiming at the problem of reliability in stereoscopic quantitative prediction of concealed ore body, and the problem of geological basis shortage and multi-solutions in magnetic forward and inverse models, a new method combining the voxel model of stereoscopic prediction of concealed ore body with magnetic forward model at the quantitative level was put forward. By use of the voxel model and the formula for magnetic charge surface integral, the mathematical model of the total magnetic field anomalies based on the voxel model of stereoscopic prediction of concealed ore bodies was deduced, the algorithm and software for solving the model were designed and developed. A case study was performed in Dingjiashan lead-zinc deposit in Youxi County, Fujian Province, China. The total magnetic field anomalies of the study area were achieved, the contour maps about theoretical total magnetic field anomalies were drawn on the basis of the known mineralization bodies, the amalgam of the predictive mineralization bodies and the known mineralization bodies, and the comparison analysis between the theoretical contour maps and the actual contour maps was made. The results show that this method, taking the voxel model as the link bridge, can achieve the coupling and complementarities of the stereoscopic quantitative prediction results of concealed ore bodies with the magnetic body forward results, and test the accuracy of the prediction results, and effectively lower the risk of the prediction of concealed ore bodies.
Key words: stereoscopic prediction of concealed ore body; voxel model; magnetic forward model
17世纪40年代,瑞典人使用罗盘寻找磁铁矿揭开了人类磁法找矿的序幕[1]。磁法勘探是通过观测和分析由岩石和矿物或其它探测对象磁性差异所引起的磁异常,进而研究地质构造和矿产资源或其它探测对象分布规律的一种地球物理方法[2-5]。磁法勘探具有轻便易行、效率高、成本低、工作领域广、地域限制小、应用范围广等优点,因此是发展最早、应用广泛的一种地球物理勘探方法[6-8]。磁法勘探在隐伏矿体预测中主要有三方面作用:划分岩体、划分构造单元及构造位置、直接(间接)找矿[9-10]。针对实际工作中的需要,我国研究人员相继开展了磁异常解释理论的研究,为我国不同纬度区磁异常特征分析与定性解释做出了很大贡献[11]。作为磁异常解释的两种定量方法:磁法正演和磁法反演,其研究对于磁法的发展具有重要推动作用。其中磁法正演反映场源与场分布特征之间的联系,是反演与解释的基础。目前,均匀的形体的正演算法研究日趋成熟[12-14],但模型简单且规则,地质依据不足,局限性很大。对于自然界中占大多数的任意复杂和物性分布并不均匀的形体,有些学者采用基于三角形多面体模型的橡皮膜技术来成功模拟并推导出正演公式[15],但在实际应用中模型难以修改、实际操作较困难,且无法满足真三维的要求。磁法反演本身存在多解性(非唯一性)问题,在非线性和三维反演中,反演对象数目往往巨大,受限于当今的计算机技术与计算方法,在超大规模方程组的求解时存在极大的困难[16-17]。而且磁法仅是从一个物性侧面来认识地质体,这就要求其解释工作必须走磁法与地质等其他方法综合研究的道路,使定性与定量结合,并对解释结果进行反复验证[18-22]。
随着国民经济对矿产资源需求的不断增大以及地表矿、浅部矿及易识别矿的日益减少, 地质找矿难度日益增大,找矿效果日益降低,危机矿山问题亟待解决,寻找隐伏矿床已经成为当前矿产预测工作的重要任务[23-24]。而传统的矿产资源定量评价的理论和方法主要是针对区域矿产资源远景预测评价工作发展起来的,尚不能完全适应危机矿山和老矿山可接替资源找矿向深边部三度空间发展的要求,迫切需要建立适应于危机矿山深边部及外围找矿的找矿创新体系与评价新理论、新技术和新方法。随着三维地质建模(3DGM)技术的发展成熟,将3DGM技术引入矿产资源定量评价,实现成矿信息三维定量提取,已逐步形成了一套适应于危机矿山深边部隐伏矿找矿特点的预测评价新技术—隐伏矿体三维可视化预测[23],在该技术中,地质体模型、成矿信息和预测成果的建立、分析和表达均是基于三维体元模型的。然而因隐伏矿的埋深大,缺乏直接的找矿标志,所以隐伏矿体预测的风险大、探索性强[24]。另外,由于地质资料收集不全和勘测误差,三维地质建模、控矿因素识别和提取都依赖于地质经验,以及在预测计算中采用了统计或非线性方法等因素的影响,使得预测成果的可靠性也有待进一步 验证。
因此,本文作者针对磁法找矿和隐伏矿体立体预测中存在的问题,以福建尤溪县丁家山铅锌矿床隐伏矿体预测为例,将三维体元模型作为磁性体正演计算与立体定量预测结合的纽带,开展了基于磁性体体元模型的磁场正演模型推导、软件开发、已知和预测的理论磁异常计算及实测磁异常对比,首次将磁性体正演计算与隐伏矿体立体定量预测结合起来,实现了地质预测与物探方法在定量层面上的有机结合,可有效地降低隐伏矿体立体定量预测的风险。
1 隐伏矿体三维可视化预测的体元模型
隐伏矿体预测的核心任务是在一定的成矿预测理论指导下,运用有效的预测方法和技术,预测工业矿化地段或矿体赋存空间位置、矿体形态以及矿化强度等特征,为勘查工程验证提供依据[25],其结合三维地质建模等技术的运用,便发展成为隐伏矿体三维可视化预测。
1.1 隐伏矿体三维可视化预测
隐伏矿体三维可视化预测的核心流程为“地质数据集成+成矿系统分析→地质信息三维建模+成矿信息定量提取→立体定量预测”,该方法属于经验模型(数据驱动)与概念模型(知识驱动)相结合的定量评价方法,它强调预测评价的三维化、定位化、定量化和精细化,以数据驱动的三维、定量、非线性建模为核心技术,追求矿化定位机制内在客观规律的探寻和三维空间中精细的定量预测评价[23]。
为达到隐伏矿体预测的立体化、定量化、数字化、和精细化的要求,必须在技术上解决矿床数字化表达、三维地质体重建、控矿地质条件定量空间分析三大关键性基础问题[26]。
三维矿床具有真三维空间特征,建立的矿床空间数据模型应当满足矿床的真三维空间特征要求和隐伏矿体立体定量预测的数字化要求,所以,空间数据模型的选择应着重考虑模型的真三维表示支持能力、模型的空间分析支持能力、模型的空间预测能力。地质对象三维建模对与矿床形成和分布相关的各种地质对象(地质体和地质场)的几何形态和空间分布进行三维几何模型与场模型的定量描述和数字化的计算机表达,不仅是建立数字矿床的基础,还是开展控矿地质条件定量分析和实现地质控矿作用定量化的前提。
因此,是否选择了合适的3D空间数据模型是地质对象的建模和表达能否实现的关键,也是统一、有效的方式解决隐伏矿体立体定量预测三大关键性问题的突破点。
从模型的角度来看,体元模型基于3D空间的体元分割和真3D实体表达,模型构造简单,体元的属性可以独立描述和存储,因而易于进行3D空间操作,现代计算机技术发展迅速,其数据存储空间大和计算速度慢的缺点都可以克服。从地质对象的角度来看,地质场具有连续变化的特性,无明确的形态边界,适于用体元模型来表达;地质体具有明确的几何表面形态或形态边界,用体元模型能表达地质对象内部的变化。
综合上述两方面考虑,尤其考虑到品位等矿体内部结构特征在三维空间分布的表达需要,本文作者采用体元模型来表达组成矿床的各种地质对象。
1.2 隐伏矿体三维可视化预测的体元模型
体元模型按体元的形状是否规则可分为规则体元模型和非规则体元模型两类。通过对模型的简洁性、实现的可能性与应用实效性对比分析,在模拟中进一步采用立方体体元模型来描述单个的地质对象。
因此,在隐伏矿体立体定量预测的不同阶段产生了相应的体元模型:矿床空间体元模型、地质体的体元模型、控矿地质因素场的体元模型、找矿信息指标的体元模型、预测成果的体元模型。
隐伏矿体预测是在一定的空间范围内进行的,当将该空间范围赋予地质意义时,称为地质空间。地质信息建模和成矿信息提取在地质空间中进行,矿化分布分析和隐伏矿体预测均限定在矿化空间范围内。因此,在三维建模前期,采用巨大的长方体包裹矿化空间、以三维栅格对矿床地质空间进行离散化,得到了矿床空间体元模型(见图1)。矿床空间体元模型具有体元定位坐标以及索引值,在空间上是所有体元模型的总和。
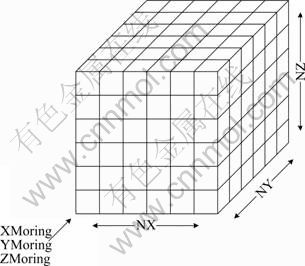
图1 矿床空间体元模型示意图
Fig. 1 Voxel model of mineralization space
根据地质建模基础数据,在单项工程及勘探线剖面三维显示的基础上,人机交互圈定地质界线并连接建立地质体的线框模型,然后利用建模软件的三维栅格化功能,对线框模型描述的地质体实体进行体元分割,赋予相应的属性值,即可得到地质体的体元模型(见图2和表1)。
表1 丁家山矿区矿体体元的属性表
Table 1 Voxel attribute table of ore bodies in Dingjiashan deposit

采用连续性的成矿物理化学方程推导的方法难以直接导出可用于隐伏矿体预测的矿化分布的定量模型,于是直接从地质条件控矿作用角度出发,以地质场来宏观地描述成矿物理化学作用在地质空间中的综合分布与控矿作用效果,通过场的离散化,可以用统计分析方法分析地质控矿作用分布与矿化分布的关联关系,从而揭示出地质条件对矿化分布控制的定量关系。此过程可以得到控矿地质因素场的体元模型(见图3)和找矿信息指标的体元模型(见表2)。
根据地质控矿作用指标变量到矿化分布指标变量映射关系的矿化泛函模型,可对未知单元的矿化指标进行估计或预测,得到预测成果的体元模型(见图4)。
表2 丁家山矿区找矿信息指标体元的属性表
Table 2 Voxel attribute table of prospecting information indexes in Dingjiashan deposit
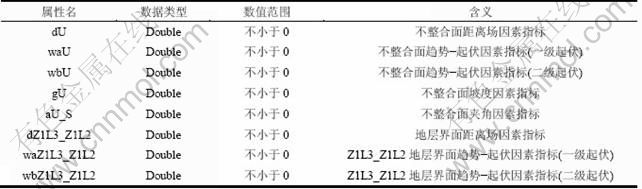

图2 丁家山铅锌矿床地质体的体元模型(矿体)
Fig. 2 Voxel models of geological bodies in Dingjiashan lead-zinc deposit (ore bodies)
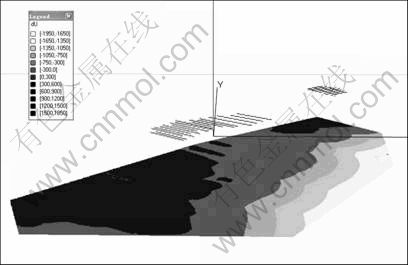
图3 控矿地质因素场的体元模型(不整合面距离场因素dU,-150 m至-200 m标高范围)
Fig. 3 Voxel model of ore-controlling geological factor fields (uncomformity surface distance field dU, from -150 m to -200 m elevation)

图4 丁家山铅锌矿床单元铅品位Pb预测结果体元模型
Fig. 4 Voxel model of prediction results for lead grade (Pb) in Dingjiashan lead-zinc deposit
2 基于三维体元模型的磁性体正演模型与实现
随着计算机的发展,正演模型已发展到利用不同的角度(二维、2.5维、三维)表达构造实体[27-28]。比如采用三维体元模型,利用其携带必要的属性信息(比如铅品位、锌品位等),可以计算出模型所产生的理论地球物理效应的数值,与实际地球物理勘探资料相比较,进而检验隐伏矿体立体定量预测成果的正确性。
2.1 基于体元模型的磁性体正演模型的公式推导
为了便于表达三维体元模型(V,见图5),不妨规定沿X坐标轴正向且垂直于X坐标轴的两个表面的代号依次为BF、FF,相应地,沿Y坐标轴、Z坐标轴正向且分别垂直于Y坐标轴、Z坐标轴的表面的代号依次为LF、RF、DF和UF。
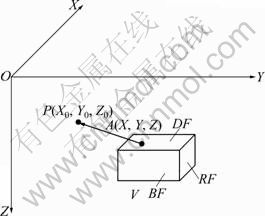
图5 三维体元模型
Fig. 5 3D voxel model
三维体元模型对空间已知P点产生的磁场强度沿3个坐标轴上的分量分别如下:
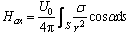 (1)
(1)
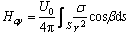 (2)
(2)
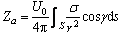 (3)
(3)
式中:Za、Hax、Hay计算的结果分别为三维体元的6个面对空间已知P点在X、Y、Z轴方向上的影响之 和,其推导结果具体如下。
1) 在求Za值中,当三维体元UF、DF投影到坐标平面XOY时:
设磁体UF或DF上有任意一点为A(X, Y, Z),空间有已知点为P(X0, Y0, Z0),在Z轴上取点C(0, 0, 1),X轴上积分区间为(a, b),Y轴上积分区间为(c, d),
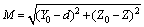 ,K=Z0-Z,
,K=Z0-Z,
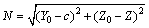 ,
,
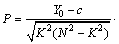
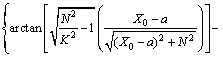
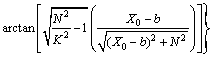 ,
,
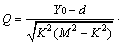
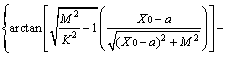
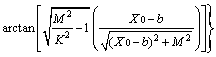 。
。
则当三维体元投影到坐标平面XOY时,Za通式为
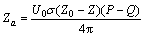 (4)
(4)
2) 在求Za值中,当三维体元LF、RF投影到坐标平面XOZ时:
设磁体LF或RF上有任意一点为A(X, Y, Z),空间有已知点为P (X0, Y0, Z0),在Z轴上取点C(0, 0, 1),X轴上积分区间为(a, b),Z轴上积分区间为(c, d),
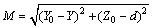 ,
,
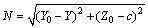 。
。
则当三维体元投影到坐标平面XOZ时,Za通式为
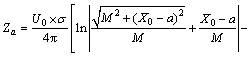
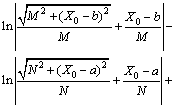
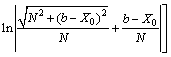 (5)
(5)
3) 在求Za值中,当三维体元FF、BF投影到坐标平面YOZ时:
设磁体FF或BF上有任意一点为A(X, Y, Z),空间有已知点为P (X0, Y0, Z0),在Z轴上取点C(0, 0, 1),Y轴上积分区间为(a, b),Z轴上积分区间为(c, d),
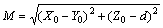 ,
,
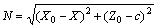 。
。
则当三维体元投影到坐标平面YOZ时,Za通式为
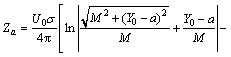
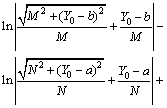
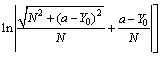 (6)
(6)
由于Hax、Hay的求法与Za类似,限于篇幅,就不再进行描述。
2.2 基于三维体元模型的磁性体正演模型计算软件设计与开发
基于三维体元模型的磁性体正演模型计算流程如下(见图6)。
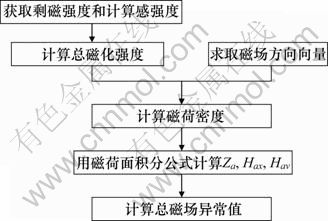
图6 基于三维体元模型的磁性体正演模型计算流程
Fig. 6 Flow for calculating magnetic body forward model based on 3D voxel model
1) 获取剩余磁化强度(Jr):根据岩矿石标本物性参数测定结果,对矿石进行定性分类,进而保证不同矿石能够得到合理的剩余磁化强度。
2) 计算总磁场异常值:利用公式?T=ZasinI+Hax· cosIcosA′+HaycosIsinA′(I为地磁倾角,A′为X轴与磁北的夹角)对研究区进行总磁场强度的计算。
在总磁场异常值求取的过程中,需要输入的参数包括:磁场的平均倾角、磁场的平均偏角、三维体元精度、真空磁导率、地磁场大小等(见图7)。
基于三维体元模型的磁性体正演模型计算所需的原始数据(预测体元、已知体元、数字高程数据)和计算结果均存储在Access 2007数据库中。
3 应用实例
丁家山铅锌矿床是属于梅仙铅锌矿田的一个大型矿床, 地处福建省尤溪县, 位于晋宁期近南北向浦城—尤溪大陆裂谷构造带南段。该区矿石品位稳定、易采选、规模大[28],通过对该矿床地质及地球化学特征研究发现,该区的铅锌矿石与磁黄铁矿、磁铁矿有较密切的共(伴)生关系,因而磁性较强,能引起中、高强度磁异常,而其围岩(绿片岩、大理岩等)基本不具磁性或弱磁性,因此磁异常可作为铅锌矿体的找矿 标志。
丁家山铅锌矿床矿体立体定量预测成果数据库中存放了大于边界品位的已知和大于边界品位的未知预测单元的矿化指标、含矿性指标的计算结果和预测结果,共有立体单元18 441个,包括已知单元5 404个、预测单元13 037个(见图8)。
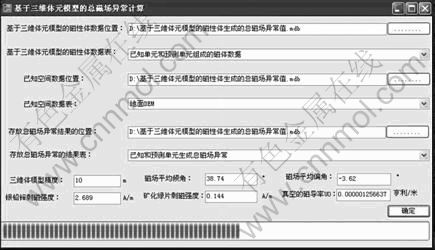
图7 基于三维体元模型的总磁场异常计算软件界面
Fig. 7 Software interface for calculating total magnetic field anomalies based on 3D voxel model
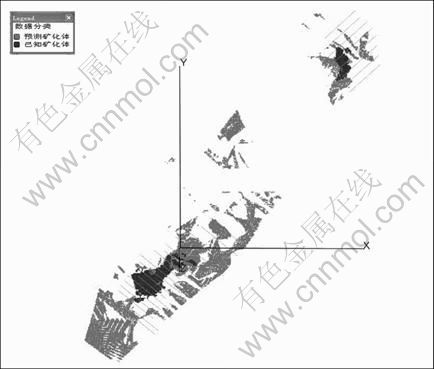
图8 已知矿化体和预测矿化体分布示意图
Fig. 8 Distribution map of known mineralization bodies and predictive mineralization bodies
3.1 基于三维体元模型的磁性体正演模型的理论 结果
在本研究中,已知磁性三维体元模型是由勘探工程穿过的三维体元、有实测样品位置落入其内的三维体元和矿体块体模型包含的磁性三维体元构成,主要分布在丁家山矿区和关兜矿区,丁家山矿区稍多。
预测磁性矿化体的在地质空间上分布广、厚度小、深度大等特性,决定了对总磁场异常影响范围比较广、数值变化不大。
依据报告中岩矿石标本磁性测定结果,将磁性矿化体进行分类:①满足w(Pb)≥0.5%或w(Zn)≥1%且(PbMet+ZnMet)>0的可视为银铅锌矿,磁导率K值的几何平均值为4 490×10-6 CGSM,Jr的几何平均值为2.689 A/m;②满足w(Pb)>0或w(Zn)>0的可视为矿化绿片岩,磁导率K值的几何平均为248×10-6 CGSM,Jr的几何平均值为0.144 A/m。除此之外,还有一些其他必要信息(见图7):1)磁场的平均倾角(38.74°);2)磁场的平均偏角(-3.62°);3)三维体元精度(10 m);4)真空磁导率(0.000 001 256 637 H/m);5)地磁场大小(46 380 nT);6)预测体元、已知体元、数字高程数据表的选择。
结合上述软件,分别计算出已知磁性三维体元、预测磁性三维体元及已知磁性三维体元数据总磁场异常,由此分别作出等值线(见图9和10)进行对比分析。
3.2 正演计算总磁异常和地面实测总磁异常结果对比分析与解释
从地面磁测获得的磁力异常图(见图11)(华东地质勘查局八一四队所测)可以看出,地面磁测表现为条带状分布,绝大部分变化幅度很小,局部变化较大,异常中心存在高值,一般都大于200 nT,对比由正演计算已知磁性矿化体的磁异常效应(见图9),两异常高值中心基本吻合,但异常高值有一定的差异,其它部分磁场方向差异更大。从正演结果可知,已知磁性矿化体引起的磁异常与地面磁测获得的目标场存在较大差异。
从图10可以看出,由正演计算已知磁性矿化体和预测磁性矿化体的总磁异常效应,其磁异场分布总体呈现由已知磁性矿化体为中心向四周降低的趋势,异常零等值线位于已知磁性矿化体和预测磁性矿化体附近,变化值为5~10 nT左右,逐步向已知磁性矿化体方向增大;负异常分布范围比较广,变化的幅度值不大,逐渐向正磁场异常中心附近减小。对比由正演计算已知矿化体的磁异常效应(见图11),正异常范围增大,局部变化增多,磁异常值有所增大。对比图11,由正演计算已知矿化体和预测矿化体的总磁异常效应在异常值变化总体趋势上和地面磁测在矿化区域比较相似。图12所示为几个相关图层的综合比较图。

图9 已知磁性矿化体产生的理论总磁场异常等值线图
Fig. 9 Contour map of theoretical total magnetic field anomalies generated from known magnetic mineralization bodies
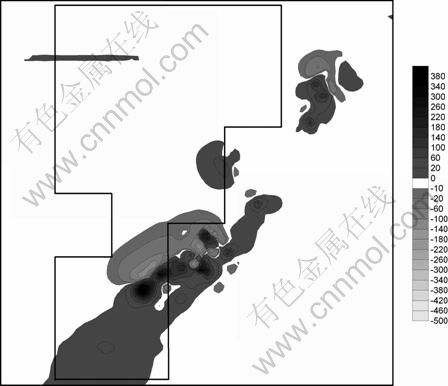
图10 已知和预测磁性矿化体产生的理论总磁场异常等值线图
Fig. 10 Contour map of theoretical total magnetic field anomaly generated from known and predictive mineralization bodies
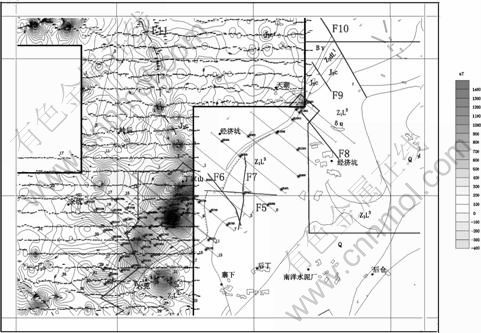
图11 丁家山矿区磁力(?T)异常平面图
Fig. 11 Map of magnetic anomalies (?T) in Dingjiashan mineral field
对比结果表明,由正演计算已知磁性矿化体和预测磁性矿化体的总磁异常,在正负异常范围和局部变化分布特征等方面,比由正演计算已知磁性矿化体的磁异常效应更接近地面磁测成果,证实了具有正负异常伴生的局部磁异常对成矿较有利,矿化体一般位于负异常与正异常之间,从而进一步确定了预测磁性矿化体的正确性。

图12 基于三维体元模型的矿化体磁异常场分布比较图
Fig. 12 Comparison of magnetic anomaly field distributions of mineralization bodies based on 3D voxel model: (a) Rendering map of terrain DEM; (b) Digital plane graph of ground magnetic point data; (c) Forward contour map of known and predicted magnetic mineralized bodies; (d) Location map of known and predicted magnetic mineralized bodies
尽管由正演计算已知矿化体和预测矿化体的总磁异常效应在异常值变化总体趋势上和地面磁测在矿化区域比较相似,但正演计算总磁异常值和实际测取的总异常值仍存在一定差异,原因如下。
1) 由于实际组成平面图的范围很大,而实际布置测量磁力点位的地点相对较少,所以一定范围地面磁测点位数据平面图本身准确度不够。
2) 充当磁性体的矿化体分布不均匀,而正演计算时假设磁性体的矿化分布均匀。
3) 磁性体附近的部分非矿化体物质已有磁性,导致总磁场异常值在一定程度上有所改变,而正演计算时没有考虑,因此正演计算结果与实测结果有所差距。
4) 感磁在矿区因时间和地点的不同而存在差异,然而,由于数据的缺失,正演计算时只能采用研究区中一点的感磁作为均值参与计算,使得正演计算结果精度不够。
5) 由于条件限制,磁导率采用真空值,这与实际地层中的磁导率存在差异,从而影响到计算结果的精度。
6) 由于实测的磁力异常是地下由浅至深各类地质体的综合叠加效应,而部分非矿区域缺失数据,因此该区域正演计算结果和实际测取总磁场异常值的差异稍大。
4 结论
1) 结合三维体元模型的特点,提出将磁法正演引入到隐伏矿化体立体定量预测中,并进行了已知磁性矿化体产生的理论总磁场异常、已知和预测磁性矿化体产生的理论总磁场异常分别与地面实地磁测对比分析,为增加隐伏矿化体立体定量预测的结果可靠性提供了全新的方法与实现途径。
2) 将提出的方法应用于福建尤溪县丁家山铅锌矿床预测结果中,得到了理论磁力异常平面图,并与实地磁力异常平面图进行对比分析,有效地检验了丁家山铅锌矿床预测结果的正确性。
3) 将三维体元模型作为磁性体正演计算与立体定量预测结合的纽带,计算了研究区的理论总磁场强度,构建了理论磁场强度和实测磁场强度的对比关系,增强了隐伏矿体立体定量预测结果可靠性,实现了体元模型的正演和隐伏矿体预测在定量层面上的有机结合,对隐伏矿体立体定量预测具有重要意义。
REFERENCES
[1] 管志宁. 地磁场与磁力勘探[M]. 北京: 地质出版社, 2005.
GUAN Zhi-ning. Geomagnetic field and magnetic exploration [M]. Beijing: Geological Publishing House, 2005.
[2] 娄德波, 宋国玺, 李 楠, 丁建华, 阴江宁, 邹 伟. 磁法在我国矿产预测中的应用[J]. 地球物理学进展, 2008, 23(1): 249-256.
LOU De-bo, SONG Guo-xi, LI Nan, DING Jian-hua, YIN Jiang-ning, ZOU Wei. The application of magnetic method in national mineral prediction[J]. Progress in Geophysics, 2008, 23(1): 249-256.
[3] 张胜业, 潘玉玲. 应用地球物理学原理[M]. 武汉: 中国地质大学出版社, 2004.
ZHANG Sheng-ye, PAN Yu-ling. Principles of applied geophysics[M]. Wuhan: China University of Geosciences Press, 2004.
[4] 王 涛, 徐鸣洁, 王良书, 刘绍文, 胡旭芝. 鄂尔多斯及邻区航磁异常特征及其大地构造意义[J]. 地球物理学报, 2007, 50(1): 163-170.
WANG Tao, XU Ming-jie, WANG Liang-shu, LIU Shao-wen, HU Xu-zhi. Aeromagnetic anomaly analysis of ordos and adjacent regions and its tectonic implications[J]. Chinese Journal of Geophysics, 2007, 50(1): 163-170.
[5] 涂广红, 江为为, 朱东英, 周立宏, 肖敦清, 高嘉瑞, 袁淑琴. 中国东北地区剩余重磁异常特征与地质构造及成矿带的关系[J]. 地球物理学进展, 2006, 21(3): 746-755.
TU Guang-hong, JIANG Wei-wei, ZHU Dong-ying, ZHOU Li-hong, XIAO Dun-qing, GAO Jia-rui, YUAN Shu-qin. The relationships between the characteristics of Northeast China residual gravity and magnetic anomalies and geological tectonic and metallogenic belt[J]. Progress in Geophysics, 2006, 21(3): 746-755.
[6] 卢 焱, 李 健, 白雪山, 李永占. 地面磁法在隐伏铁矿勘查中的应用—以河北滦平号铁矿为例[J]. 吉林大学学报: 地球科学版, 2008, 38(4): 698-702.
LU Yan, LI Jian, BAI Xue-shan, LI Yong-zhan. Application of magnetic survey on hidden iron deposit prospecting—Case study on luanping iron deposit in Hebei province, China[J]. Journal of Jilin University: Earth Science Edition, 2008, 38(4): 698-702.
[7] 邓月红, 黄 甫. 高精度磁法在滁州黄道山寻找隐伏岩体的应用[J]. 矿业快报, 2007, (5): 78-79.
DENG Yue-hong, HUANG Pu. The application of searching hidden-rock based on high-precision magnetic method in Chuzhou, China[J]. Express Information of Mining Industry, 2007, (5): 78-79.
[8] 王聿军, 仲卫国, 张善法. 金伯利岩的物化探特征及勘探方法[J]. 地球物理学进展, 2005, 20(1): 108-111.
WU Yu-jun, ZHONG Wei-guo, ZHANG Shan-fa. The geophysical and geochemical abnormal features and prospection methods of Kimberlite[J]. Progress in Geophysics, 2005, 20(1): 108-111.
[9] 于长春, 范正国, 王乃东, 熊盛青, 万建华, 张洪瑞. 高分辨率航磁方法及在大冶铁矿区的应用[J]. 地球物理学进展, 2007, 22(3): 979-983.
YU Chang-chun, FAN Zheng-guo, WANG Nai-dong, XIONG Sheng-qing, WAN Jian-hua, ZHANG Hong-rui. High-resolution aeromagnetic exploration methods and their application in Daye Iron Mines[J]. Progress in Geophysics, 2007, 22(2): 979-983.
[10] 严加永, 滕吉文, 吕庆田. 深部金属矿产资源地球物理勘查与应用[J]. 地球物理学进展, 2008, 23(3): 871-891.
YAN Jia-yong, TENG Ji-wen, LU Qing-tian. Geophysical exploration and application of deep metallic ore resources[J]. Progress in Geophysics, 2008, 23(3): 871-891.
[11] 肖敦辉, 董方灵. 三维重磁人机交互解释的剖面成体建模方法[J]. 地理与地理信息科学, 2009, 25(5): 26-29.
XIAO Dun-hui, DONG Fang-ling. Method of building 3D geological model from sections during gravity & magnetic interactive interpretation[J]. Geography and Geo-Information Science, 2009, 25(5): 26-29.
[12] BARNETT C T. Theoretical modeling of the magnetic and gravitational fields of an arbitrarily shaped three dimensional body[J]. Geophysics, 1976, 41(6): 1353-1364.
[13] OKABE M. Analytical expressions for gravity anomalies due to homogeneous polyhedral bodies and translations into magnetic anomalies[J]. Geophysics, 1979, 44(4): 730-741.
[14] 何昌礼, 钟本善. 复杂形体的高精度重力异常正演方法[J]. 物探化探计算技术, 1988, 10(2): 121-128.
HE Chang-li, ZHONG Ben-shan. A high accuracy forward method for gravity anomaly of complex body[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1988, 10(2): 121-128.
[15] XIA Heng-ren, HANSEN R, HARTHILL N, TRAYNIN P. Interactive modeling of potential fields in three dimensions[C]// Proceedings of SEG 63 Annual International Meeting: Expanded Abstracts. Washington, 1993: 403-404.
[16] 管志宁, 侯俊胜, 黄临平, 姚长利. 重磁异常反演的拟BP神经网络方法及其应用[J]. 地球物理学报, 1998, 41(2): 242-251.
GUAN Zhi-ning, HOU Jun-sheng, HUANG Lin-ping, YAO Chang-li. Inversion of gravity and magnetic anomalies using pseudo-BP neural network method and its application[J]. Chinese Journal of Geophysics, 1998, 41(2): 242-251.
[17] FEDI M, RAPOLLA A. 3-D inversion of gravity and magnetic data with depth resolution. Geophysics, 1999, 64: 452-460.
[18] 姚长利, 郝天珧, 管志宁, 张聿文. 重磁遗传算法三维反演中高速计算及有效存储方法技术[J]. 地球物理学报, 2003, 46(2): 254-258.
YAO Chang-li, HAO Tian-yao, GUAN Zhi-ning, ZHANG Yu-wen. High speed computation and efficient storage in 3-D gravity and magnetic inversion based on genetic algorithms[J]. Chinese Journal of Geophysics, 2003, 46(2): 254-258.
[19] 李 军. 基于Marquardt算法重磁复杂形体三维全局反演研究[D]. 成都: 成都理工大学, 2005: 1-55.
LI Jun. The study of 3D-visualization inversion for gravity and magnetism complex bodies based on Marquardt algorithms[D]. Chengdu: Chengdu University of Technology, 2005: 1-55.
[20] 刘光鼎, 郝天珧. 应用地球物理方法寻找隐伏矿床[J]. 地球物理学报, 1995, 38(6): 850-854.
LIU Guang-ding, HAO Tian-yao. Searching of hidden mineral deposits by geophysical methods[J]. Chinese Journal of Geophysics, 1995, 38(6): 850-854.
[21] 贾进斗, 何展翔, 孔繁恕. 非地震综合物化探技术应用及效果[J]. 石油地球物理勘探, 1998, 33(5): 625-631.
JIA Jin-dou, HE ZHan-xiang, KONG Fan-shu. The applications and effects of comprehensive non-seismic geophysical and geochemical exploration techniques[J]. OGP, 1998, 33(5): 625-631.
[22] 敬荣中. 地球物理非线性联合反演方法研究[D]. 长沙: 中南大学, 2002: 1-98.
JING Rong-zhong. The study of non-linear geophysical integration inversion methods[D]. Changsha: Central South University, 2002: 1-98.
[23] 毛先成, 邹艳红, 陈 进, 赖健清, 彭省临, 邵拥军, 疏志明, 吕俊武, 吕才玉. 危机矿山深部、边部隐伏矿体的三维可视化预测—以安徽铜陵凤凰山矿田为例[J]. 地质通报, 2010, 29(2/3): 401-413.
MAO Xian-cheng, ZOU Yan-hong, CHEN Jin, LAI Jian-qing, PENG Sheng-lin, SHAO Yong-jun, SHU Zhi-ming, L? Jun-wu, L? Cai-yu. Three-dimensional visual prediction of concealed ore bodies in the deep and marginal parts of crisis mines: A case study of the Fenghuangshan ore field in Tongling, Anhui, China [J]. Geological Bulletin of China, 2010, 29(2/3): 401-413.
[24] 赵鹏大, 李紫金, 胡光道. 重点成矿区三维立体矿床统计预测—以安徽月山地区为例[M]. 武汉: 中国地质大学出版社, 1992: 107-108.
ZHAO Peng-da, LI Zi-jin, HU Guang-dao. Three dimensional statistical prediction of deposit in key metallogenic region: An example from Yueshan area in Anhui Province[M]. Wuhan: China University of Geosciences Press, 1992: 107-108.
[25] 滕吉文, 杨立强, 姚敬全, 刘宏臣, 刘 财, 韩立国, 张雪梅. 金属矿产资源的深部找矿、勘探与成矿的深层动力过程[J]. 地球物理学进展, 2007, 22(2): 317-334.
TENG Ji-wen, YANG Li-qiang, YAO Jing-quan, LIU Hong-chen, LIU Cai, HAN Li-guo, ZHANG Xue-mei. Deep discover ore exploration and exploitation for metal mineral resources and its deep dynamical process of formation[J]. Progress in Geophysics, 2007, 22(2): 317-334.
[26] 毛先成, 戴塔根. 隐伏矿体立体定量预测[M]. 北京: 地质出版社, 2010: 10-12.
MAO Xian-cheng, DAI Ta-gen. Research on stereoscopic quantitative prediction of concealed ore bodies[M]. Beijing: Geological Publishing House, 2010: 10-12.
[27] 朱海龙. 电磁模拟与反演研究组简介[J]. 勘探地球物理进展, 2006, 29(2): 149-150.
ZHU Hai-long. Electromagnetic simulation and inversion study group introduction[J]. Progress in Exploration Geophysis, 2006, 29(2): 149-150.
[28] 高 铁, 吴燕冈, 郭 华, 马淑颜. 二维重磁资料联合正演模拟[J]. 吉林大学学报: 地球科学版, 2006, 36(1): 20-22.
GAO Tie, WU Yan-gang, GUO Hua, MA Shu-yan. Joint direct modeling 2D gravimetric and magnetic data[J]. Journal of Jilin University: Earth Science Edition, 2006, 36(1): 20-22.
(编辑 何学锋)
基金项目:国家“十二五”科技支撑计划资助项目(2011BAB04B10);国家自然科学基金资助项目(41172297)
收稿日期:2011-11-14;修订日期:2012-01-02
通信作者:毛先成,教授,博士;电话:0731-88877571; E-mail: xcmao@126.com