J. Cent. South Univ. Technol. (2010) 17: 129-135
DOI: 10.1007/s11771-010-0021-7 
Wheel slip-sinkage and its prediction model of lunar rover
DING Liang(丁亮)1, 2, GAO Hai-bo(高海波)1, 2, DENG Zong-quan(邓宗全)1, 2, TAO Jian-guo(陶建国)1, 2
1. Aerospace Mechanism and Control Key Laboratory of Fundamental Science for National Defense,
Harbin Institute of Technology, Harbin 150001, China;
2. State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150001, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2010
Abstract: In order to investigate wheel slip-sinkage problem, which is important for the design, control and simulation of lunar rovers, experiments were carried out with a wheel-soil interaction test system to measure the sinkage of three types of wheels in dimension with wheel lugs of different heights and numbers under a series of slip ratios (0-0.6). The curves of wheel sinkage versus slip ratio were obtained and it was found that the sinkage with slip ratio of 0.6 is 3-7 times of the static sinkage. Based on the experimental results, the slip-sinkage principle of lunar’s rover lugged wheels (including the sinkage caused by longitudinal flow and side flow of soil, and soil digging of wheel lugs) was analyzed, and corresponding calculation equations were derived. All the factors that can cause slip sinkage were considered to improve the conventional wheel-soil interaction model, and a formula of changing the sinkage exponent with the slip ratio was established. Mathematical model for calculating the sinkage of wheel according to vertical load and slip ratio was developed. Calculation results show that this model can predict the slip-sinkage of wheel with high precision, making up the deficiency of Wong-Reece model that mainly reflects longitudinal slip-sinkage.
Key words: lunar rover; slip-sinkage; loose lunar soil; stress distribution; slip ratio
1 Introduction
In the 1990s, the second lunar exploration upsurge was set off in the world. Lunar rovers are important instruments that are expected to perform advanced scientific tasks during the upcoming missions. The “Chang’e-1” lunar orbiter of China was launched up successfully in 2007 and a rover is planned to launch up for exploring the moon before 2013. Researchers of the world have been devoting their attention to the related technologies of lunar rovers and its landers for several years [1-3].
The surface of the moon is very rough, covered with a thick soft regolith layer composed of dust and rock clast. While moving on such a challenging terrain, severe slip-sinkage will occur for rover’s wheels, making the vehicle decrease tractive performance, deviate from scheduled path, and even get stuck in the soil. Slip- sinkage is an important failure form for the planetary rovers moving on deformable terrain. YOSHIDA and HIROSHI [2] described the process observed in experiments. In 2005, it took 5 weeks for the “Opportunity” Mars Rover to escape from the Purgatory Dune after getting stuck.
Terramechanics, with which the slip-sinkage problem of planetary rover can be analyzed, is currently a hot subject of research. Terramechanics theory is widely used for the research of rovers, including mechanical design [3-4], performance evaluation [4-5], simulation [6-7], soil parameter identification [8-9], mobility control [10-11], and path planning [12]. The Mars Base Technology Program (MBTP) of National Aeronautics and Space Administration in USA is now supporting Carnegie Mellon University (CMU) and Massachusetts Institute of Technology (MIT) to research on the related technologies for Mars rover based on terramechanics.
Researching on the slip-sinkage problem is of great importance for design, control and high-fidelity simulation of lunar rover. At present, conventional terramechanics models such as Bekker model [13] and Wong-Reece model [14-15] developed for terrestrial vehicles are usually directly used for analyzing the wheel-soil interaction mechanics of planetary rovers. However, the former model can only calculate the static sinkage of a wheel, without considering the dynamic sinkage caused by wheel slip; the latter can reflect the slip-sinkage caused by longitudinal motion of soil to some extent, but it does not consider that resulting from lateral flow of soil and soil digging by the lugs. Due to the remarkable differences between terrestrial vehicles and planetary rovers in running environment, physical dimension, load, velocity, and control mode, the applicability of the conventional theory should be examined and some new problems are brought forward. YOSHIDA and ISHIGAMI [16], SHIBLY et al [17], BROOKS et al [18], BAUER et al [19], and TAO et al [20] did theoretical and experimental investigation of terramechanics for planetary rovers. However, the slip- sinkage of rover wheel is still less considered.
Wheel-soil interaction experiment is the basis of terramechanics research. With the wheel-soil interaction test system developed for planetary rovers, experiments were carried out to measure the sinkage of three types of wheels with different dimensions and wheel lugs under a series of slip ratios. The factors that can lead to slip sinkage were analyzed based on the experimental results. Finally, a model for calculating the entire sinkage of wheel, including slip-sinkage, was derived and verified.
2 Experimental
2.1 Equipment
The wheel-soil interaction test system developed in our laboratory (as shown in Fig.1) was used to perform the experiments. The system consists of three motors (driving motor, carriage motor and steering motor) and related sensors (linear potentiometer displacement sensor, six-axis F/T sensor, torque sensor, current sensors and optical encoders). The driving motor can drive the wheel to move forward; the carriage motor is used together with a conveyance belt to imitate the influence of vehicle body on the wheel and create various slip ratios; while the steering motor is used for steering performance research. The wheel sinkage is measured by the high precision sliding resistance displacement sensor. The output voltage of which is 0-10 V, corresponding to a displacement of 0-150 mm with high linearity precision.

Fig.1 Wheel-soil interaction test system
2.2 Wheel and planetary soil simulant
The experimental wheels were designed referring to the current planetary rovers and technical specification of China’s lunar rover. Three types of cylindrical metal wheels with different dimensions (radius r by width b) of 135.0 mm×165.0 mm (Wh1), 135.0 mm×110.0 mm (Wh2), and 157.4 mm×165.0 mm (Wh3) were used. Lugs of different heights (h=5, 10 and 15 mm) can be installed to the smooth wheels with various numbers (nL=30, 24, 15, 8, …).
The volcanic ash has similar physical and chemical properties with the lunar soil and can be used to make lunar soil simulant. But the producing procedure is complex and the expense is high. Literatures show that the mechanical properties of dry loose sand are similar to those of planetary soil. So it was usually used as planetary soil stimulant [17]. The lunar soil simulant used in this work was made from soft sand after removing impurities, sieving, ventilating and drying.
2.3 Conditions
Three groups of experiments were designed to investigate the influence on sinkage of wheel dimension, lug height h and lug number nL (as shown in Table 1). The maximum velocity of China’s lunar rover under development is approximately 55 mm/s (200 m/h), which is comparable to that of the current Mars rovers. Experiments show that the variance of velocity that is lower than 55 mm/s has little impact on wheel-soil interaction mechanics. So the moving velocity of wheel is set to 10 mm/s. In order to avoid serious slip-sinkage, the slip ratio of exploring rovers should be measured and controlled, for instance, the maximum slip ratio of Mars rovers of USA is restricted to be less than 0.4. The experimental slip ratios were 0, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5 and 0.6. The vertical wheel load of lunar rover is several dozens of Newton, for example, if the mass of a six-wheel rover is 120 kg, the average vertical load is about 33 N. The wheel lugs make the vertical load fluctuate with an altitude of approximately ±20 N. In order to reduce the relative error, the vertical load is set to 80 N. The vertical load has little influence on the experimental conclusions.
Table 1 Test and corresponding wheels
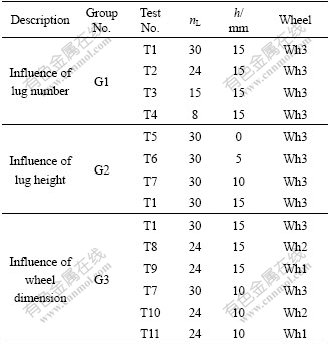
2.4 Results
Fig.2 shows Wh1 wheel installed with lugs of 10 mm in height and slip ratios of 0.2 and 0.6, respectively. It can be seen from Fig.2 that the wheel sinkage increases significantly and the stripes of wheel traces become more intensive with the increment of slip ratio (s). During the process of wheel-soil interaction, the wheel sinkage fluctuates periodically accompanying with the entrance and leaving of wheel lugs. Experimental data acquisition period was 0.15 s, as a result, hundreds of raw data could be obtained for a test.

Fig.2 Slip-sinkage of wheel Wh1: (a) s=0.2; (b) s=0.6
Let v and ω denote linear velocity and angular velocity of wheel, respectively. The slip ratio is defined as:
 (1)
(1)
The fluctuating frequency of wheel sinkage increases with the increment of slip ratio and the cycle T can be calculated as follows:
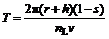 (2)
(2)
The reference of measuring the sinkage is the lowest point on cylindrical surface of wheel, that is to say, the height of lugs is not considered. The wheel interacts with the soil to achieve a steady state after running for several seconds. The steady data were used to calculate the mean value of sinkage after filtering. In order to verify the repeatability of experiment, some of the experiments were carried out three times. Experimental results show that the mean values of sinkage several times are almost the same despite of the fluctuation of data, proving the repeatability and consistency of experiments. Processing the original data obtained by experiments of more than 100 times, the curves of sinkage versus slip ratio were drawn, as shown in Figs.3-5.
Seen from Fig.3, which illustrates the wheel sinkage varying with the slip ratio for Wh3 with different numbers of lugs, it can be concluded that the wheel sinkage increases from 5 to 30 mm if the slip ratio increases from 0 to 0.6, and the wheel lug has little influence on it.
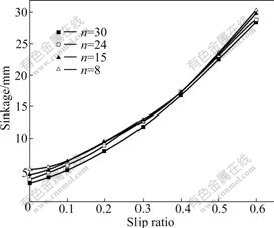
Fig.3 Influence of wheel’s lug number on slip-sinkage
Fig.4 shows the slip-sinkage curves of Wh3 with lugs of different heights. The slip-sinkage phenomenon is obvious for all the wheels. If the slip ratio is less than 0.4, the higher the lugs are, the smaller the sinkage will be. This shows that the lugs play a certain role in sustaining the wheel, and the effect is more obvious for wheel with higher lugs. Or else, if the slip ratio is greater than 0.4, the wheel sinkage will be larger for the wheels with higher lugs because the digging soil effect of lugs plays more important roles. For wheels with lugs of 10 and 15 mm in height, the slip-sinkage phenomenon is more evident. If the wheel lugs are low, the slip of soil mainly occurs at the surface between wheel surface and soil; but it occurs between the steady soil and movable soil adhering to the wheel if the wheel lugs are high enough to form steady shearing loop. The friction angle of metal and soil is smaller than the internal friction angle of soil. The larger friction causes larger slip-sinkage.

Fig.4 Influence of wheel’s lug height on slip-sinkage
Fig.5 shows the slip-sinkage of wheels with different dimensions. The wheel sinkage is increased with decreasing the width or radius of wheels. The increasing gradient of sinkage with the slip ratio is less influenced by the dimensions, which is mainly affected by the height of wheel lugs. The higher the wheel lugs are, the larger the gradient of sinkage is.
All the wheels exhibit severe slip-sinkage phenomena. The sinkage at the slip ratio of 0.6 is 3-7 times of the sinkage at the slip ratio of 0, which greatly increases the soil resistance and the probability of wheel stuck. Controlling the slip ratio under 0.4 can restrict the wheel sinkage effectively, as well as avoid the slip-sinkage caused by soil digging of lugs.
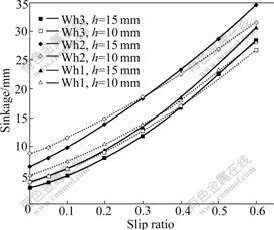
Fig.5 Influence of wheel’s dimension on slip-sinkage
3 Wheel slip-sinkage process analysis
3.1 Slip-sinkage of smooth wheel
3.1.1 Longitudinal slip-sinkage
All the wheels of lunar rover are driven wheels to exert maximum tractive performance. The wheel interacts with soil and two shear flow failure regions, i.e., ABC and ADE form, as illustrated in Fig.6 [21], where θ1.is the entrance angle, θ2 is the leaving angle, θm is the angle corresponding to point A, as well as the maximum stress angle. The instantaneous center I is situated above bottom-dead-center O of wheel. Soil of region ABC has a movement in the same direction of wheel motion and moves the soil forward to form a bow wave. Soil of region ADE has an opposite moving direction. The soil is bulldozed backward so that slip-sinkage is caused. The envelope of the two regions can be expressed with logarithmic spiral curves and straight lines. AF is spiral curve with the function of:
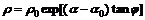 (3)
(3)
DF is a straight line with an angle of Xc to the horizontal plane; Xc equals π/4-φ/2, where φ is the internal friction angle of soil; and σ1 is the maximum principal stress of point A. According to theory of plasticity mechanics, the characteristic lines i and j intersect with the line of σ1 at Xc angle. The movement direction of point A on the wheel rim is the sliding direction of soil, the same as the characteristic line j. Parameters of Eq.(3) are:
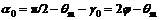 (4)
(4)
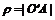 (5)
(5)
where ρ0 is determined by the coordinates of point A and O′. (xA, yA)=(rsin θm, r(1-cos θm)), (xE, yE)=(rsin θ2, r(1-cos θ2)), then the coordinates of point O′ is derived as follows:
 (6)
(6)
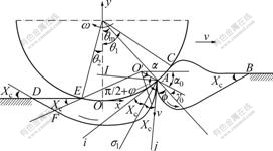
Fig.6 Diagram of soil’s shear flow failure
Considering that the soil of sliding shearing region ADE sticks to the wheel to become a part of it, the wheel will get additional sinkage while rotating with adhered soil. Fig.7 illustrates the process.
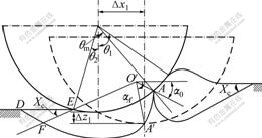
Fig.7 Diagram of slip-sinkage of lunar rover’s wheel
The slip-sinkage caused by longitudinal flow of soil can be calculated with the following equation:
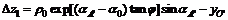 (7)
(7)
where the angle of 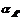 can be solved by the following equation:
can be solved by the following equation:
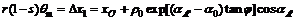
(8)
The maximum stress angle θm=(c1+c2s)θ1 increases with the increment of slip ratio s, where c1 and c2 are parameters related to the properties of lunar soil, then the envelope region of line AFD will be larger, making the slip sinkage become larger.
3.1.2 Slip-sinkage caused by lateral flow of soil
As the flow of soil particles is three-dimensional, besides the slip-sinkage resulting from longitudinal flow of soil, the lateral flow of it can also cause slip-sinkage, which is denoted by Δz2. Literature shows that the soil beneath wheels with large vertical load or large sinkage is easier to flow laterally [20]. Lateral slip-sinkage is more severe for the narrow lunar rover wheels. As the theory of soil lateral flow is lacking, the slip-sinkage caused by lateral flow of soil can be studied with experimental methods.
3.2 Influence of wheel lugs on slip-sinkage
3.2.1 Slip-sinkage caused by soil digging of lugs
Fig.8 shows the slip-sinkage caused by wheel lugs. Let θc (θc=θ2-θ1) denote the wheel-soil interaction angle, tc denote the time for the wheel to rotate for such an angle, Δx3 denote the travelling distance corresponding to the angle of θa without slip. Then, we have
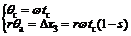 (9)
(9)
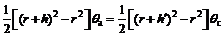 (10)
(10)
According to Eqs.(9) and (10), one can obtain:
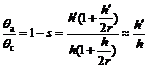 (11)
(11)
The slip-sinkage caused by soil digging of lugs is:
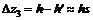 (12)
(12)
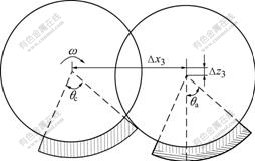
Fig.8 Diagram of slip-sinkage caused by wheel lugs
3.2.2 Supporting effect of lugs
The soil acts at the top end of the lugs and the wheel is somewhat supported by the resulted supporting force, thus the wheel sinkage can be reduced to some extent. At the same time, the end parts of higher lugs can enter the soil to support the wheel more easily. For the lunar rover wheels, the thickness of lugs is usually quite small so that the vertical load is primarily balanced with the force acted on the cylindrical surface of wheel, rather than the lugs. As a result, the sinkage decreased by the lugs is relatively small. By analyzing the experimental results, one can conclude that a constant value Δz4 can be used to describe the decrement of sinkage caused by supporting effect of wheel lugs approximately.
4 Wheel slip-sinkage prediction model
In order to calculate the longitudinal slip-sinkage with Eq.(7), the leaving angle and maximum stress angle should be calculated firstly. However, it is also difficult to determine the angles; at the same time, the unknown static sinkage and slip-sinkage caused by lateral flow of sand are also necessary for calculating the entire wheel sinkage. Different sinkages correspond to different normal stresses and shear stresses, by which the vertical load is balanced. The wheel sinkage relates to the vertical load and stress distribution, and the slip ratio primarily influences the stress distribution to cause slip-sinkage. Therefore, the wheel sinkage can be solved by force balancing according to analysis of stress distribution.
4.1 Wheel-soil interaction mechanics
Fig.9 shows the diagram of wheel-soil interaction mechanics, where z is the slip-sinkage, W is vertical load of wheel, FDP is the resistance of moving forward (W and FDP are forces acted on the wheel by the vehicle body through axle), and T is the driving torque of motor. The soil interacts with the wheel in the form of continuous normal stress σ and shear stress τ. Improving the Wong-Reece normal stress model [14] and Janosi shear stress model [22] for the lugged wheel of lunar rover with high slip-sinkage, Eqs.(13)-(19) for calculating the stress distribution and concentrated force were obtained. Eq.(13) is used to change the constant sinkage exponent with the slip ratio for predicting the slip-sinkage caused by lateral flow of soil. Eq.(14) can reflect the influence on soil displacement of wheel lugs. Eq.(15) is used to calculate the leaving angle of wheel. n0, n1 and c are parameters related to wheel-soil interaction. Eq.(16) can calculate the equivalent radius, and λ is 0.5 in this study. The stresses and vertical load are calculated by Eqs.(17)- (19), which are also improved corresponding to Eqs.(13)-(16).
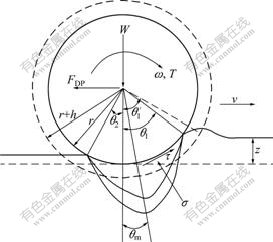
Fig.9 Wheel-soil interaction mechanics diagram
N=n0+n1s (13)
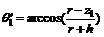 (14)
(14)
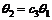 (15)
(15)
Req=r+λh, 0≤λ≤1 (16)
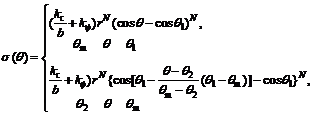 (17)
(17)
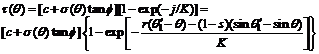 (18)
(18)

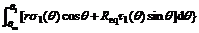 (19)
(19)
4.2 Wheel sinkage prediction model and verification
Equation for calculating wheel sinkage is:
z=z0+Δz1+Δz2+hs-Δz4 (20)
Substituting the given wheel load W and slip ratio s into Eq.(19), the entrance angle θ1 could be solved. According to the entrance angle, the summation of the former three terms in Eq.(20), i.e., the static sinkage z0 and the two slip-sinkages caused by soil flow, can be obtained as follows.
z0+Δz1+Δz2=r(1-cos θ1) (21)
Then the entire wheel sinkage of the given slip ratio can be calculated with the following equation:
z=r(1-cos θ1)+hs-Δz4 (22)
Given a vertical load of 80 N, changing the slip ratio to calculate the wheel sinkage, the theoretical and experimental curves are compared in Fig.10. Wong-Reece model can reflect the longitudinal slip- sinkage, which is smaller than 5 mm. By changing the sinkage exponent with slip ratio, the slip-sinkage caused by lateral flow of soil can also be predicted, which is a primary part of the slip-sinkage. For the wheel of Wh2, n0=0.93, n1=0.54;and for Wh3, n0=0.84, n1=0.72. For the wheel with lugs of 10 mm in height, Δz4 is 1.5 mm; while Δz4 is 3 mm for the wheel with lugs of 15 mm in height. It can be concluded that if continuous shearing loop is formed, the height of wheel lugs has little influence on the flow of soil, and the difference of wheel sinkage, which is relatively small, is mainly caused by supporting and soil digging of lugs.
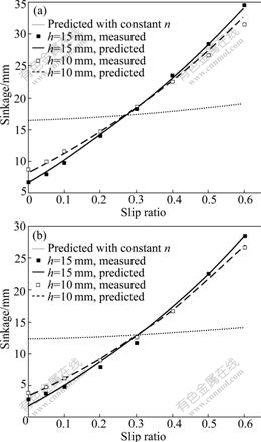
Fig.10 Comparison of predicted and experimental results of sinkage: (a) Wh2; (b) Wh3
5 Conclusions
(1) The number of wheel lug has little influence on the wheel sinkage, while the lug height has obvious influence on it. However, if continuous shearing loop is formed, the height of wheel lugs has little influence on the flow of soil, and the difference of wheel sinkage, which is relatively small, is mainly caused by supporting and soil digging of lugs.
(2) All the wheels exhibit severe slip-sinkage. The sinkage at the slip ratio of 0.6 is 3-7 times of the sinkage at the slip ratio of 0, which greatly increases the resistance and the probability of wheel stuck. Controlling the slip ratio under 0.4 can restrict the wheel sinkage effectively, as well as avoid the slip-sinkage caused by soil digging of lugs.
(3) The slip-sinkage of lunar rover’s wheel is caused by the longitudinal/lateral flow of soil, soil digging of wheel lugs, etc. Changing the sinkage exponent with slip ratio, a mathematic model for predicting wheel sinkage given vertical load and slip ratio is derived. Calculation results show that this model can predict the slip-sinkage of wheel with high precision, making up the deficiency of Wong-Reece model that mainly concerns longitudinal slip-sinkage.
(4) The results of theoretical analysis and experimental research on wheel slip-sinkage can be applied to the design, control and high-fidelity dynamics simulation of lunar rover, as well as for the terrestrial vehicles and other mobile robots such as Mars rovers in similar environment.
References
[1] WANG Shao-chun, DENG Zong-quan, HU Ming, GAO Hai-bo. Dynamic model building and simulation for mechanical main body of lunar lander [J]. Journal of Central South University of Technology, 2005, 12(3): 329-334.
[2] YOSHIDA K, HIROSHI H. Motion dynamics of a rover with slip-based traction model [C]// Proceedings of IEEE International Conference on Robotics and Automation. Piscataway: IEEE Robotics and Automation Society, 2002: 3155-3160.
[3] APOSTOLOPOULOS D S. Analytical configuration of wheeled robotics locomotion [R]. Pittsburghers: Robotics Institute of Carnegie Mellon University, 2001.
[4] MICHAUD S, RICHTER L, THUER T, GIBBESCH A, HUELSING T. Rover chassis evaluation and design optimization using the RCET [C]// Proceedings of the 9th ESA Workshop on ASTRA. Noordwijk: European Space Agency, 2006: 1-8.
[5] PATEL N, ELLERY A, ALLOUIS E, SWEETING M, RICHTER L. Rover mobility performance evaluation tool (RMPET): A systematic tool for rover chassis evaluation via application of Bekker theory [C]// Proceedings of the 8th ESA Workshop on ASTRA. Noordwijk: European Space Agency, 2004: 251-258.
[6] SOHL G, JAIN A. Wheel-terrain contact modeling in the ROAMS planetary rover simulation [C]// Proceedings of IDETC’05 ASME International Design Engineering Technical Conference and Computers and Information in Engineering Conference. New York: American Society of Mechanical Engineers, 2005: 1-9.
[7] PIERRE L, ROLAND S. Wheel torque control in rough terrain: Modeling and simulation [C]// Proceedings of IEEE International Conference on Robotics and Automation. Piscataway: IEEE Robotics and Automation Society, 2005: 867-872.
[8] HUTANGKABODEE S, ZWEIRI Y H, SENEVIRATNE L D, ALTHOEFER K. Performance prediction of a wheeled vehicle on unknown terrain using identified soil parameters [C]// Proceedings of IEEE International Conference on Robotics and Automation. Piscataway: IEEE Robotics and Automation Society, 2006: 3356- 3361.
[9] IAGNEMMA K, KANG S, SHIBLY H, DUBOWSKY S. Online terrain parameter estimation for wheeled mobile robots with application to planetary rovers [J]. IEEE Transactions on Robotics, 2004, 20(5): 921-927.
[10] ISHIGAMI G, MIWA A, NAGATANI K, YOSHIDA K. Terramechanics-based model for steering maneuver of planetary exploration rovers on loose soil [J]. Journal of Field Robotics, 2007, 24(3): 233-250.
[11] IAGNEMMA K, DUBOWSKY S. Traction control of wheeled robotic vehicles with application to planetary rovers [J]. International Journal of Robotics Research, 2004, 23(10): 1029-1040.
[12] ISHIGAMI G, NAGATANI K, YOSHIDA K. Path planning for planetary exploration rovers and its evaluation based on wheel slip dynamics [C]// Proceedings of IEEE International Conference on Robotics and Automation. Piscataway: IEEE Robotics and Automation Society, 2007: 2361-2366.
[13] BEKKER M G. Introduction to terrain-vehicle [M]. Michigan: The University of Michigan Press, 1969.
[14] WONG J Y, REECE A R. Prediction of rigid wheel performance based on analysis of soil-wheel stresses, part I: Performance of driven rigid wheels [J]. Journal of Terramechanics, 1967, 4(1): 81-98.
[15] WONG J Y. Theory of ground vehicles [M]. 3rd ed. New York: John Wiley & Sons, 2001.
[16] YOSHIDA K, ISHIGAMI G. Steering characteristics of a rigid wheel for exploration on loose soil [C]// Proceedings of IEEE International Conference on Intelligent Robots and Systems, Piscataway: IEEE Robotics and Automation Society, 2004: 3995-4000.
[17] SHIBLY H, IAGNEMMA K, DUBOWSKY S. An equivalent soil mechanics formulation for rigid wheels in deformable terrain, with application to planetary exploration rovers [J]. Journal of Terramechanics, 2005, 42: 1-13.
[18] BROOKS C A, IAGNEMMA K, DUBOWSKY S. Visual wheel sinkage measurement for planetary rover mobility characterization [J]. Autonomous Robotics, 2006, 21: 55-64.
[19] BAUER R, LEUNG W, BARFOOT T. Experimental and simulation results of wheel-soil interaction for planetary rovers [C]// Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway: IEEE Robotics and Automation Society, 2005: 586-591.
[20] TAO Jian-guo, QUAN Qi-quan, DENG Zong-quan, WANG Lin. Analysis of wheel-soil interaction of rolling wheels with different diameters on a lunar rover [J]. Journal of Harbin Engineering University, 2007, 28(10): 1144-1149. (in Chinese)
[21] ZHUAN Ji-de. Computational vehicle terramechanics [M]. Beijing: China Machine Press, 2002. (in Chinese)
[22] JANOSI Z, HANAMOTO B. Analytical determination of drawbar pull as a function of slip for tracked vehicle in deformable soils [C]// Proceeding of the 1st International Conference of ISTVES. Torino: International Society for Terrain-Vehicle Systems, 1961: 707-726.
Foundation item: Project(50975059) supported by the National Natural Science Foundation of China; Project(2006AA04Z231) supported by the National High-Tech Research and Development Program of China; Project(ZJG0709) supported by Key Natural Science Foundation of Heilongjiang Province of China; Project(B07018) supported by the Program of Introducing Talents of Discipline to University; Project (SKLRS200801A02) supported by Chinese State Key Laboratory of Robotics and System Foundation
Received date: 2009-03-10; Accepted date: 2009-06-07
Corresponding author: DING Liang, PhD; Tel: +86-451-86402037; E-mail: liang.ding@hotmail.com
(Edited by YANG You-ping)