不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用
柳建新,蒋鹏飞,童孝忠,徐凌华,谢 维,王 浩
(中南大学 信息物理工程学院,湖南 长沙,410083)
摘 要:基于双二次插值的有限单元法求解大地电磁二维正演问题,以不均匀网格剖分为基础,推导出大地电磁响应的计算公式。针对有限单元法最后形成一个线性方程组,系数矩阵是大型稀疏的带状对称正定复系数矩阵,并且其条件数远大于1,为严重病态矩阵,求解其对应方程组会遇到很多困难等问题,采用不完全LU分解(即上三角与下三角分解)处理的稳定双共轭梯度算法(BICGSTAB算法)求解该线性方程组,通过对层状介质和二维模型电磁响应进行计算,获得二维大地电磁的视电阻率曲线和阻抗相位曲线。研究结果表明,BICGSTAB算法具有速度快、精度高和稳定性好等优点。
关键词:大地电磁;有限单元法;二维正演;不完全LU分解;BICGSTAB算法
中图分类号:P631.3 文献标识码:A 文章编号:1672-7207(2009)02-0484-08
Application of BICGSTAB algorithm with incomplete LU decomposition preconditioning to two-dimensional magnetotelluric forward modeling
LIU Jian-xin, JIANG Peng-fei, TONG Xiao-zhong, XU Ling-hua, XIE Wei, WANG Hao
(School of Info-physics and Geomatics Engineering, Central South University, Changsha 410083, China)
Abstract: Based on the finite element method of quadratic interpolation in a rectangular element to solve the two-dimensional magnetotelluric forward problem, no-uniform mesh based magnetotelluric responses calculation formula was derived. Based on the fact that the finite element method was used to form a linear equation, and the coefficient matrix was a large sparse, banded, symmetric, conditioned and complex matrix, its condition number is far larger than 1, and it was an ill-conditioned matrix, solving large scale ill-conditioned linear equation was very difficult, and so the BICGSTAB (Bi-conjugate gradient stabilized method) algorithm with incomplete LU decomposition for preconditioning was used to solve this system linear equation. This approach was verified through the calculations of layered earth model and two-dimensional earth model. The results show that the BICGSTAB algorithm has high speed, high precision and stability. The apparent resistivity curves and the impedance phase curves are very accurate to synthetic magnetotelluric responses.
Key words: magnetotelluric; finite element method; two-dimensional forward modeling; incomplete LU decomposition; BICGSTAB algorithm
大地电磁测深法(MT)从20世纪50年代被提出以来,经过50多年的发展,在理论方法研究、数据处理和资料解释与应用等方面都取得了很大发展。与其他地球物理勘探方法一样,正演问题是大地电磁测深法数据处理的关键所在。国外很早就开始了大地电磁场的数值模拟研究,如Coggon[1]提出用有限单元数值模拟方法计算大地电磁场,有限单元模拟大地电磁场,从能量最小原理推导出亥姆霍兹方程的有限元格 式;Wannamaker等[2]提出一个高准确性的有限单元算法,研究了二维带地形正演问题,主要是通过提高所求辅助场的精度,来提高算法的整体精度;Pridmore等[3]也有限单元法正演方面进行了研究。国内陈乐寿 等[4-10]也对大地电磁的二维有限元正演方面进行了研究。本文作者在前人研究的基础上,采用双二次插值的有限单元法,对求解区域采用非均匀网格剖分,最后形成1个大型稀疏对称正定线性方程组。直接求逆计算该线性方程组需要的运算量和存储需求将超出系统承受能力,迭代算法成为求解这类问题的首要问题。不同的迭代算法需要的存储容量和计算的复杂度也不同,收敛速度不同,为此,人们提出了许多低计算复杂度和低存储容量的方法[11-14]。BICGSTAB算法(Bi-conjugate gradient stabilized method)是Van和Vorst等[14-15]在CGS(Conjugate gradient squared),BICG (Bi-conjugate gradient)和GMRES(General minimalized residual)上发展起来的,它具有CG(Conjugate gradient)的优点,也可以与预处理技术(Precondition technology)以及多网格方法结合使用,而且算法非常有效和 稳定。
1 大地电磁二维正演
1.1 边值问题
假定地下电性结构是二维的,取走向为x轴正向,y轴与x轴垂直,保持水平,z轴垂直向下(见图1)。当平面电磁波以任何角度入射地面时,地下介质的电磁波总以平面波形式,几乎垂直向下传播。根据Maxwell方程,并考虑到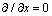 ,得2个独立的方程组,并以x分量为准,分别命名为电场平行(TE)和磁场平行(TM)极化模式。
,得2个独立的方程组,并以x分量为准,分别命名为电场平行(TE)和磁场平行(TM)极化模式。

图1 大地电磁二维正演研究区域
Fig.1 Studied area of two-dimensional forward modeling in magnetotelluric
TE极化模式:

TM极化模式:

由式(1)和(2)可知,Ex和Hx满足的偏微分方程为:
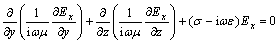 ;
;
(3)
 。
。
(4)
于是,式(3)和(4)可统一表示成:
 。 (5)
。 (5)
对于TE极化模式,有:
 ;
; ;
; 。 (6)
。 (6)
对于TM极化模式,有:
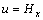 ;
;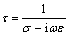 ;
;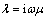 。 (7)
。 (7)
边界问题归纳为[7]:
 (8)
(8)
1.2 变分问题
边值问题式(8)与下列变分问题等价[7]:
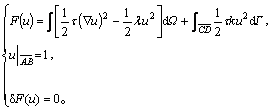
(9)
2 有限单元法
2.1 矩形单元双二次插值
采用矩形单元将整个区域剖分(见图2),矩形单元双二次插值是在每个单元上取8个点:4个顶点和4条边的中点,编号及坐标见图2(a)所示的母单元,图2(b)所示为子单元,两者的坐标关系为:
 ,
,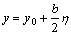 。 (10)
。 (10)
其中:x0和y0为子单元的中点;a和b为子单元的2个边长。2个单元的微分关系为:
 ,
,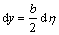 ,
,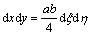 。 (11)
。 (11)
构造形函数,双二次插值的形函数为:
 (12)
(12)

(a) 母单元;(b) 子单元
图2 双二次插值矩形单元
Fig.2 Rectangular element of quadratic interpolation
单元积分为:
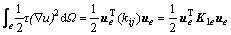 。 (13)
。 (13)
其中: ;
; ;
;
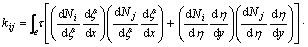
 。 (14)
。 (14)
于是,可得:
 ?
?

 。
。
单元积分为:
 。 (15)
。 (15)
其中: ;
; ;
;
 。 (16)
。 (16)
于是可得:
 。
。
单元积分为:
 。 (17)
。 (17)
其中:
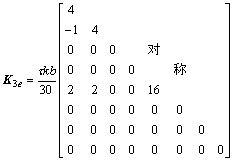 。
。
将K1e,K2e和K3e扩展成全体节点组成的矩阵,由全部单元相加得:

 。 (18)
。 (18)
其中: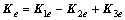 ,
, 。
。
对式(18)求变分并令其等于0,得线性方程组:
 。 (19)
。 (19)
加入上边界条件,解方程组即可得各节点得u。
当计算出各节点的u值后,再利用数值方法求出场值沿垂向的偏导数 ,代入以下2式便可计算视电阻率和阻抗相位。
,代入以下2式便可计算视电阻率和阻抗相位。
对TE极化方式:
 (20)
(20)
对TM极化方式:
 (21)
(21)
2.2 不均匀网格剖分
用有限单元法求解大地电磁测深二维正演问题。首先,对研究区域进行剖分,节点与单元遍及整个研究区域,将连续函数的求解化为节点上离散函数值的求解。因此,网格及疏密对函数值的计算产生重要的影响。对无穷远边界条件的近似处理方式,加大了边界对计算结果的影响,测量点距离边界越近,边界的影响就会越大,误差也越大。这就要求边界应尽可能远,以便得到比较满意的结果,但这必须增加网格的数量,相应地也就增加了计算机内存的需求量和计算时间。为了解决这一矛盾,将整个区域划分为2个区域:目标区域和网格外延区域,如图3所示。目标区域为地质体赋存区域,也是数据的采集区域。以均匀网格剖分,网格外延区域的网格步长按大于1的倍数递增,在保证计算精度的情况下,减少网格剖分数,减少计算时间。
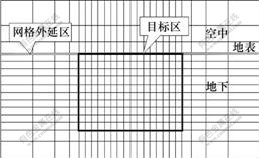
图3 不均匀网格剖分
Fig.3 Non-uniform grid
3 线性方程组求解
3.1 BICGSTAB算法
BICGSTAB算法的主要思想是基于双边Lanczos算法和基于残差正交子空间的迭代方法。对于n阶线性方程组Ax=b,假设初始近似解为x0,第k次近似解为xk,相应的第k次残差rk=b-Axk, 有关的k阶Krylov子空间,并且
有关的k阶Krylov子空间,并且 ,
,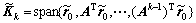 。单边Lanczos算法在残差子空间Kk中通过特定的规则迭代,使得残差趋于0,从而得到方程的解,而且这种迭代是有限次的。BICGSTAB算法则在Krylov子空间Kk中选取序列pk,通过选择合适的参数
。单边Lanczos算法在残差子空间Kk中通过特定的规则迭代,使得残差趋于0,从而得到方程的解,而且这种迭代是有限次的。BICGSTAB算法则在Krylov子空间Kk中选取序列pk,通过选择合适的参数 和
和 ,使得按式(1)产生序列的xk和rk,满足
,使得按式(1)产生序列的xk和rk,满足 且
且 ,同时,计算的残差rk总是取最小范数。
,同时,计算的残差rk总是取最小范数。
 ;
; ;
;
 。 (22)
。 (22)
这种基于Krylov残差子空间的迭代方法收敛速度快,精度高,而且稳定性好。BICGSTAB算法常常与预优技术结合处理方程求解问题,一般流程如下:
a. 给定系数矩阵A,向量b,初始值x0最大迭代次数kmax,最大容许误差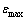 以及预优矩阵M,计算
以及预优矩阵M,计算 ,并令k=1,
,并令k=1,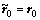 。
。
b. 若k≤kmax且ε≥εmax,则转3),否则,停止,输出xk。
c.  。若
。若 或者
或者 ,则算法终止,输出失败信息,否则转4)。
,则算法终止,输出失败信息,否则转4)。
d. 若k=1,则 ,否则,计算
,否则,计算
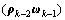 ,
, 。
。
e. 求解方程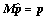 ,计算
,计算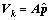 ,
,
 ,
, 。
。
f. 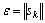 ,若
,若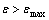 ,则
,则 ,否则,停止输出
,否则,停止输出 。
。
g. 求解 ,
, ,
, ,
,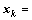
 ,
,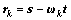 ,
, ,令k=k+1,转2)。
,令k=k+1,转2)。
3.2 不完全LU分解预处理
预处理矩阵M采用不完全LU分解。若系数矩阵A的顺序主子式矩阵都是非奇异的,则矩阵A一定能进行LU分解。若A是一个大型稀疏矩阵,则它的因子L和U的下、上三角部分一般来说都是满的矩阵。若取预处理矩阵M=LU,则理论上最好(不需考虑),但实际上这完全行不通。一种不完全LU分解是指把A分解为 和
和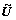 ,它们对应的元素与L和U对应的元素相同,但2个因子分别与A的下、上三角部分有完全相同的非零结构。这种分解就是无填充的不完全LU分解,记为ILU(0)。其中,“0”代表因子分解是产生的非零元素的个数为0。
,它们对应的元素与L和U对应的元素相同,但2个因子分别与A的下、上三角部分有完全相同的非零结构。这种分解就是无填充的不完全LU分解,记为ILU(0)。其中,“0”代表因子分解是产生的非零元素的个数为0。
3.3 算例
在大地电磁二维正演问题中,由有限元单元法离散化导出的线性代数方程组(其系数矩阵记为K)主要有以下基本特征:
a. K是稀疏的。网格节点一般是很多的,但每一个节点上的离散化方程只联系几个相邻节点,除与这些节点对应的未知解的系数非零外,其余系数都是0,所以,系数矩阵的元素大量是0,这就是系数矩阵的稀疏性。
b. K是对称并且是正定的。
c. K一般都是病态的。若K的条件数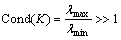 (
( 和
和 分别为矩阵K的
分别为矩阵K的
绝对值最大特征值与最小特征值)时,称K是病态矩阵。当K是病态矩阵时,求解其对应方程组会遇到很多困难。
图4(a)所示为大地电磁二维正演计算中双二次插值有限单元法形成的总体刚度矩阵的非零元素分布,其非零元素有9 641个;图4(b)和图4(c)所示为采用不完全LU分解后的上、下三角矩阵非零元素分布图,其非零元素均有5 151个。该图的横坐标表示矩阵的行,纵坐标表示矩阵的列。采用不完全LU分解预处理的BICGSTAB算法求解该线性复系数方程组,给出一定的容许相对误差,迭代适当的次数即得到方程组的解,如图5所示。

(a) 双二次插值形成的刚度矩阵;(b) L矩阵;(c) U矩阵
图4 不完全LU分解
Fig.4 Incomplete LU decomposition
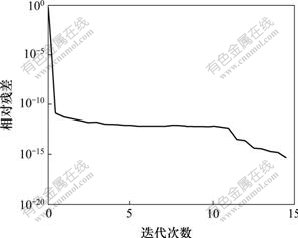
图5 BICGSTAB算法迭代误差
Fig.5 Iteration error in BICGSTAB algorithm
4 正演模拟
4.1 层状介质
模型为2层G型地电模型,模型参数为ρ1=100 ??m,ρ2=600 ??m,h1=1.8 km。用有限单元法双二次插值法对TE极化模式和TM极化模式分别采用20×26 (4个空气层)和20×22的剖分单元进行计算,延伸的空气层厚度为3 km,并将计算结果与理论解析结果进行对比(图6)。从图6可以看出,在10-3~104 s周期范围内,2种极化模式的视电阻率和阻抗相位曲线与理论值曲线较吻合。双线性插值法视电阻率和阻抗相位曲线的首枝出现突变异常,误差较大;而双二次插值法视电阻率和阻抗相位曲线与理论值曲线较吻合,首枝变化也不大,误差较小。这说明在网格剖分相同的条件下,双二次插值的精度远高于双线性插值的精度。

(a) TE视电阻率;(b) TE阻抗相位;(c) TM视电阻率;(d) TM阻抗相位
图6 双二次插值和双线性插值计算结果与理论值对比
Fig.6 Comparison of computing results with synthetic results
4.2 二维模型
该模型为包含异常体的3层层状介质模型。表层的电阻率为50 ??m,厚度约为200 m;第2层的电阻率为100 ??m,厚度约为750 m,在这层的中间位置,有1个低阻异常,宽度为4 km,深度约为500 m,电阻率为10 ??m;最下层的电阻率为1 k??m,如图7所示。

图7 复杂二维模型
Fig.7 Complicated two-dimensional model
正演模拟中,TE极化模式和TM极化模式分别采用90×29 (6个空气层)和90×23的剖分单元进行正演模拟,延伸的空气层厚度为6.3 km。图8(a)所示是频率为100 Hz时模拟所得的视电阻率曲线,图8(b)所示是频率100 Hz时模拟所得的阻抗相位曲线,二者均真实反映了模型的地电参数,说明本文的算法对二维大地电磁正演模拟是有效的。

(a) 视电阻率; (b) 阻抗相位
1—TE极化模式;2—TM极化模式
图8 复杂二维模型正演模拟结果
Fig.8 Results of forward modeling for a two-dimensional model
5 结 论
a. 采用双二次插值有限单元法在大地电磁二维正演计算中形成的总体刚度矩阵为大型稀疏对称正定复系数矩阵,其条件数远大于1,为严重病态矩阵,求解其对应方程组会遇到很多困难。
b. BICGSTAB迭代方法是求解病态线性方程组的一种稳定方法,为了节省计算机内存,采用不完全LU分解作为预处理矩阵。不完全LU分解处理的BICGSTAB算法具有速度快、精度高和稳定性好等优点。
c. 通过对层状介质和二维模型大地电磁响应的计算,获得了二维大地电磁的视电阻率曲线和阻抗相位曲线,验证了算法的正确性,也为大地电磁的资料处理和解释工作提供经验。
参考文献:
[1] Coggon J H. Electromagnetic and electrical modeling by the finite element method[J]. Geophysics, 1971, 36(1): 132-155.
[2] Wannamaker P E, Stodt A, Rijo L. Two-dimensional topographic responses in magnetotelluric modeled using finite elements[J]. Geophysics, 1971, 36(7): 2131-2144.
[3] Pridmore D F, Hohmann G W, Sill W. An investigation of finite element modeling for electrical and electromagnetic data in three dimensions[J]. Geophysics, 1981, 46(5): 1009-1024.
[4] 陈乐寿, 刘 任, 王天生. 大地电磁测深资料处理与解释[M]. 北京: 石油工业出版社, 1989: 224-240.
CHEN Le-shou, LIU Ren, WANG Tian-sheng. The magnetotelluric sounding data processing and interpretation methods[M]. Beijing: Petroleum Industry Press, 1989: 224-240.
[5] 刘小军, 王家林, 于 鹏. 基于二次场的二维大地电磁有限元数值模拟[J]. 同济大学学报, 2007, 35(8): 1113-1117.
LIU Xiao-jun, WANG Jia-lin, YU Peng. Secondary field-based two-dimensional magnetotelluric numerical modeling by finite element method[J]. Journal of Tongji University, 2007, 35(8): 1113-1117.
[6] 徐世浙, 刘 斌. 电导率分层连续变化的水平层的大地电磁正演[J]. 地球物理学报, 1995, 38(2): 262-268.
XU Shi-zhe, LIU Bin. A numerical method for calculating MT field on a layered model with continuous change of conductivity in each layer[J]. Chinese Journal of Geophysics, 1995, 38(2): 262-268.
[7] 徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994: 255-259.
XU Shi-zhe. Finite element method for geophysics[M]. Beijing: Science Press, 1994: 255-259.
[8] 陈小斌, 张 翔, 胡文宝, 等. 有限元直接迭代算法在MT二维正演计算中的应用[J]. 石油地球物理勘探, 2000, 135(4): 487-496.
CHEN Xiao-bin, ZHANG Xiang, HU Wen-bao, et al. Application for direct iterative finite element in MT 2D forward computation[J]. Oil Geophysical Prospecting, 2000, 135(4): 487-496.
[9] 黄临平, 戴世坤. 复杂条件下3D电磁场有限元计算方法[J]. 中国地质大学学报, 2002, 27(6): 775-779.
HUANG Lin-ping, DAI Shi-kun. Finite element calculation method of 3D electromagnetic field under complex condition[J]. Journal of China University of Geosciences, 2002, 27(6): 775-779.
[10] 王 若, 王妙月, 卢元林. 三维三分量CSAMT法有限元正演模拟研究初探[J]. 地球物理学进展, 2007, 22(2): 579-585.
WANG Ruo, WANG Miao-yue, LU Yuan-lin. Preliminary study on 3D 3C CSAMT method modeling using finite element method[J]. Progress in Geophysics, 2007, 22(2): 579-585.
[11] 刘万勋, 刘长学, 华波浩. 大型稀疏线性方程组的解法[M]. 北京: 国防工业出版社, 1981: 85-120.
LIU Wan-xun, LIU Chang-xue, HUA Bo-hao. The solution for the large-scale sparse linear equations[M]. Beijing: National Defense Industry Press, 1981: 85-120.
[12] 徐树方. 矩阵计算的理论和方法[M]. 北京: 北京大学出版社, 1991: 154-168.
XU Shu-fang. Theory and methods for matrix computation[M]. Beijing: Peking University Press, 1991: 154-168.
[13] Vogel G L. Multigrid reconditioned conjugate gradient method for large-scale wave-front reconstruction[J]. Journal of the Optical Society of America, 2002, 19(9): 1817-1822.
[14] Van D, Vorst H. Iterative solution methods for certain sparse linear systems with a nonsymmetric matrix arising from PDE-problems[J]. Journal of Computational Physics, 1981, 44(1): 1-19.
[15] Van D, Vorst H. Bi-CGSTAB: A fast and smoothly converging variant of BI-CG for the solution of nonsymmetric linear systems[J]. SIAM Journal on Computing, 1992, 13(2): 631-644.
收稿日期:2008-05-10;修回日期:2008-08-06
基金项目:国家自然科学基金资助项目(60672042);教育部博士点基金资助项目(20070533102)
通信作者:柳建新(1962-),男,湖南岳阳人,博士,教授,博士生导师,从事大地电磁理论研究;电话:13807486248;E-mail: ljx6666@126.com