J. Cent. South Univ. Technol. (2007)04-0575-05

DOI: 10.1007/s11771-007-0110-4

Analytical method of load-transfer of single pile under expansive soil swelling

FAN Zhen-hui(范臻辉)¹, WANG Yong-he(王永和)¹, XIAO Hong-bin(肖宏彬) ^1,2, ZHANG Chun-shun(张春顺) ¹

(1. School of Civil and Architectural Engineering, Central South University, Changsha 410075, China;

2. Institute of Geotechnical Engineering, Hunan University of Technology, Zhuzhou 412008, China)

__________________________________________________________________________________________

Abstract: The elastic differential equations of load-transfer of single pile either with applied loads on pile-top or only under the soil swelling were established, respectively, based on the theory of pile-soil interaction and the shear-deformation method. The derivation of analytic solution to load-transfer for single pile in expansive soil could hereby be obtained by means of superposition principle under expansive soils swelling. The comparison of two engineering examples was made to prove the credibility of the suggested method. The analyzed results show that this analytic solution can achieve high precision with few parameters required, indicating its’ simplicity and practicability in engineering application. The employed method can contribute to determining the greatest tension along pile shaft resulting from expansive soils swelling and provide reliable bases for engineering design. The method can be employed to obtain various distributive curves of axial force, settlements and skin friction along the pile shaft with the changes of active depth, vertical movements of the surface and loads of pile-top.

Key words: expansive soil; pile; shear-deformation method; load transfer

__________________________________________________________________________________________

1 Introduction

The expansive soil is a kind of particular clay that is mainly composed of hydrophilic mineral montmorillonite and illite, which has apparent swelling- shrinkage behavior with changes of water content^[1]. It is widely distributed around the world^[2], such as the half regions of the USA, Sudan and Algeria in Africa, Israel and central regions of India in Asia, Spain in Europe, Argentina in South America, and China is no exception with many provinces, such as Yunan, Guangxi, Hunan, Hebei, Henan, Hubei, Anhui, and Sichuan, being reported on expansive soils problems sometimes. The deformation of structures above the expansive soils is caused by apparent swelling-shrinkage behavior of the soils with changes of water content, which is different from the common foundation systems whose settlements are controlled by soil compressibility and strength. To the engineering constructions in the area of expansive soils, piles are commonly used to be digged into deep soil layer with no apparent change of water content, which may greatly decrease the upward movements of the structures. Since pile is inserted into expansive soils, it must be pulled by upward shear force transmitted from the soil to the pile. If the upward shear force is great enough, the pile may even be broken by such great tension.

COLLINS suggested an expression to calculate tensile stress of the pile based on the assumption that slippage occurs between pile and expansive soils at the interface^[3]. Thus, the shear stress is equal to cohesive stress at the pile-soil interface. However, the expression could only obtain the stress of the pile but not reflect the pile displacement. Afterward, many scholars suggested different methods to analyze pile behaviors in expansive soils, among which the FEM (finite element method), with no doubt, is a good method^[4-8]. Nevertheless, so many parameters are required in using FEM, which limits its application in engineering. In this paper, an analytical solution to the load-transfer law of single pile in expansive soils was derived, which is based on both the interactive rules of the pile-soil and the swelling effect of expansive soil.

2 Basic assumptions of pile-soil analysis

The following assumptions are adopted in deriving the analytical solution:

1) The cross-section is constant along the pile, without considering the non-linear compressive behavior, and the pile can bear compressive and tensile stress.

2) The expansive soils behavior is described by elastic constitutive relationships and principles of continuum mechanics, with no change after the addition of water.

3) The heave varies linearly along the depth from the maximum value s₀ on the ground surface, to zero at the active depth:

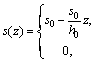
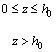          (1)

where  s(z) are heaves at different depths within the active zone; h₀ is the active depth; s₀ is the heave of the ground surface.

4) Downward direction is regulated to be positive.

3 Theoretical analysis and derivation

The complexity of studying the pile-expansive soils behavior is mainly referred to two aspects. On the one hand, the pile with applied load will move downwards, which results in downward movement of the soil around; on the other hand, the soil around may be counteracted by the pile when soil swelling. Under the two kinds of loads, the relative difference in movement between the soil and pile will result in complex distribution of the pile axial stress as well as the skin friction.

To be convenient, the problem can be divided into two parts: the pile only with applied loads; the pile only with expansive soil swelling in the foundation.

3.1 Load-transfer law for single pile under applied load

Many tests in-room and in-situ show that vertical downward displacement of the soil around the pile w_s1(r, z) relates not only with the soil depth z but also with the distance r away from pile axes when pile is loaded. Moreover, with the increase of r, w_s1(r, z) will decrease logarithmically ^[9]. Thus, assumption below is available:

w_s1(z, r)=f₁(z)ln(r_m/r)          (2)

where  f₁(z) is the vertical displacement function related to the depth; r_m is the maximum effective radius of pile on the soil around, generally r_m=2.5L(1-ν_S); L is pile length; ν_S is Poisson ratio of the pile lateral soil.

According to the displacement compatible condition at interface of pile-soil, we obtain:

f₁(z)=w_p1(z)/ξ               (3)

where  w_p1(z) is the axial displacement of pile when loaded on the pile top; ξ is the effective parameter of the pile radius, ξ=ln(r_m/r₀); r₀ is the radius of the pile.

Inserting Eqn.(3) into Eqn.(2), we have

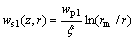         (4)

If the effect of radial movements is ignored, shear stress (τ_s1) of any point in the soil can be obtained in terms of elastic theory:

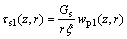        (5)

Assume r=r₀ in Eqn.(5), and then the pile’s skin friction can be obtained:

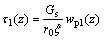         (6)

where  G_s is the lateral soil’s shear modulus of the pile.

The vertical displacement of the sub-layer under the pile end can be calculated by Boussinesq theory when loaded with P_b1:

w_b1=n_bP_b1             （7）

where  n_b=η(1-ν_b)/(4r_bG_b); η is an effective parameter of pile-end displacement, generally η=0.5-1.0^[9-10]; ν_b is Poisson ratio of the pile-end soil; r_b is the radius of the pile-end, in this paper, r_b=r₀; G_b is the shear modulus of the pile-end soil; w_b1 is the displacement of pile-end.

The relation between the skin friction and the axial force of pile is like below when loaded:

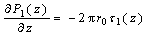         (8)

where  P₁(z) is the axial force at the depth of under loads on the pile-top; r₀ is the radius of the cross-section of the pile; τ₁(z) is the pile’s skin friction at the depth of z.

The relation between axial force of pile and pile displacement is

         (9)

where  E_p is the elastic modulus of the pile; A_p is the area of the cross-section of the pile.

Inserting Eqn.(6) into Eqn.(8)，and then solving the simultaneous equations composed of Eqns.(8) and (9), we obtain

       (10)

where  μ²=2/(ξλ_pr²₀), λ_p=E_p/G_s.

Solving Eqn.(10), we get

w_p1(z)=C₁sinh(μz)+C₂cosh(μz)         (11)

where  C₁ and C₂ are integral constants, which may be obtained by the following boundary conditions:

      (12)

After obtaining the integral constants C₁ and C₂, place them back into Eqn.(11)，then we obtain

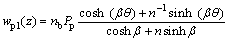 (13)

where  β=μL；n=E_pA_pμn_b；θ=1-z/L。

Placing Eqn.(13) into Eqn.(9), we obtain

     (14)

3.2 Load-transfer law of single pile only with expansive soils swelling

The expansive soils swelling may affect the pile-soil behavior in two aspects. On the one hand, the pile will be pulled upwards by the lateral swelling soil, and if the upward shear force is large enough, the pile-end resistance would even be zero; on the other hand, the pile’s skin friction may counteract the soil swelling around the pile, and the nearer the distance away from the pile axes, the more the counteraction. Assume the displacement function of the pile side soil is like below in terms of the interactive rules of the pile-soil^[11-12]:

w_s2(z, r)=-s(z)+f₂(z)ln (r_m/r)      (15)

According to compatible condition of the vertical displacements^[13], the vertical displacement function related to depth can be obtained:

          (16)

Placing (16) into (15), we get

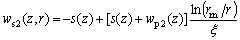  (17)

where  w_p2(z) is the pile’s axial displacement induced by expansive soil swelling. Ignoring the effect of radius displacement, shear stress of any point in soil can be calculated in terms of elastic theory:

        (18)

Putting r=r₀ to Eqn.(8), the skin friction at the interface between the pile and the soil under expansive soil swelling can be obtained:

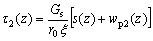          (19)

Similarly, elastic differential equation of pile can be obtained considering both the relation of pile’s skin friction to pile axial force and the that of pile axial force to pile displacement:

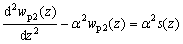      (20)

where  α²=2π/(λ_pA_pξ). Placing Eqn.(1) into Eqn.(20), we have

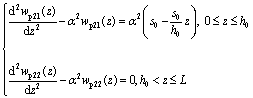     (21)

The boundary conditions for Eqn.(21) are as follows:

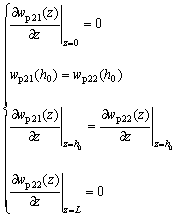    (22)

So Eqn.(21) can be solved and the result is as follows:

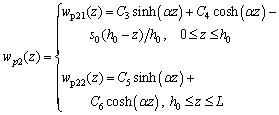  (23)

where  ，

,

 ，

.

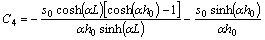In terms of the relation of pile axial force to pile displacement, we obtain

 (24)

3.3 Load-transfer law under both applied loads on pile-top and effect of expansive soil swelling

When pile bears the applied loads as well as the effect of soil swelling, the expressions as follows by means of superposition principle can be obtained:

w_p(z)=w_p1(z)+w_p2(z)             (25)

P(z)=P₁(z)+P₂(z)               (26)

τ(z)=τ₁(z)+τ₂(z)                (27)

4 Examples and analysis

Example 1 DONALDSON inserted a concrete pile with the diameter of 22.86 cm and the length of 10.36 m in expansive soil. A steel pipe was placed in the center of the pile in order to fix facilities to keep observing for a long time^[3]. POULOS et al^[3] used FEM to make analysis of the pile. To make comparison, the author employed the suggested method to calculate the pile and parameters used in Poulos’s calculation were adopted in this study. The parameters required for calculation are as follows: pile diameter d=22.86 cm，pile length L=10.36 m，pile’s elastic modulus E_p=20 GPa，the compression modulus of soil E_s=12 MPa, Poisson ratio ν_s=0.3, movement of the top of the expansive soil s₀=10 mm, active depth h₀＝5.18 m. The relation between shear modulus and modulus of compressibility is 

          (28)

Fig.1 shows the result of pile axial force along the pile shaft obtained by the suggested method in this study. Because it is a free pile with no applied load, axial forces are tensile along the entire pile shaft. From Fig.1, good agreement among the calculated results, test results and Poulos’s results could be found. It is noted that the axial forces obtained by the suggested method above the middle of pile are a little bit greater. This is mainly because the G_s in this study is assumed constant, which does not fully agree with the reality. Soil’s G_s near the surface of the soil is smaller than that of soil deeply beneath the surface. Actually, G_s increases nonlinearly from the top of soil to the end. So the suggested method shows closer agreement under the middle of the pile.

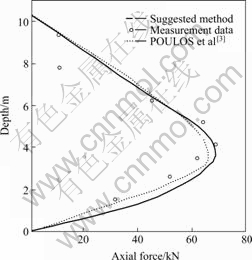
Fig.1 Relation between axial forces and depths only under soil swelling

Example 2 Model test study: The test was carried out in a jerrican with the diameter of 50 cm and the height of 90 cm. Cobbles were placed from the bottom to the height of 10 cm, fine sands of 12 cm were filled on the cobbles layer, and the Nanning expansive soil (middle swelling grade) with the height of 58 cm was filled on the sands layer. The model pile was a PVC pipe with the diameter of 5 cm and the length of 65 cm. In the jerrican, the model pile was put into the depth of 58 cm before the soil was filled. 10 pieces of strain-gauges were sticked on the pile outer surface symmetrically, and the distance of each one from the pile-top was 8, 22, 36, 50, 64 cm, respectively(see Fig.2). The responding axial force of each cross-section could be calculated by means of Hooke rules since the strain could be measured by the electrical measurement. In the test, the soil’s modulus of compressibility E_s=7 MPa, elastic modulus of pile E_p=1.82 GPa, the max vertical movement of the soil’s surface was 4.2 cm，and pile’s vertical movement was 1.98 cm. In this study, Poisson’s ratio was 0.3，active depth was 0.58 m, and the vertical movements were assumed to vary linearly from the soil surface to the active depth. The pile axial stresses along the shaft and the pile vertical upward displacements are shown in Figs.3 and 4, respectively, obtained by the suggested method. Close agreement can be found in Fig.3, showing the feasibility of the employed method.

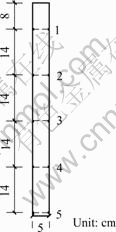
Fig.2 Scheme of model pile and strain-gauges’ position

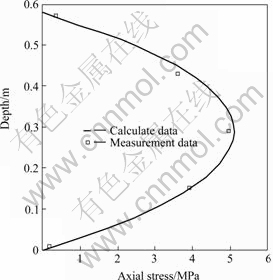
Fig.3 Relation between axial stress and depths

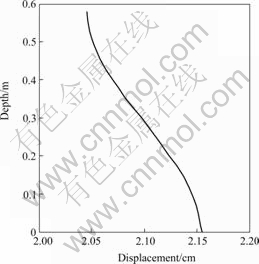
Fig.4 Relation between axial displacement and depth

From the two examples above, the suggested method performs very high accuracy and needs less parameters. It is credible and simple to be used in engineering practice.

5 Conclusions

1) The load-transfer law for single pile considering the expansive soil swelling behavior was analyzed. An engineering practice and a model test were given to compare the test results with those obtained by the suggested method, and very close agreement was found to ensure the credibility of the suggested method. What’s more, the suggested method is simple, practical and of high accuracy.

2) The suggested method can directly calculate the maximum tensile force induced by swelling for engineering design. Moreover, it can also obtain the distribution of axial force, pile displacement and pile’s skin friction along the pile shaft, with different active depths, different heaves of the surface and different applied loads on the pile-top.

3) The key point in the suggested method is to identify the shear modulus when it is employed to analyze the load-transfer law for single pile in expansive soils. In this study, the ground is assumed isotropic while actually, ground is composed of different soil layers with different soil behaviors. So the weighted average of each elastic modulus could be adopted as the required elastic modulus to ground with different layers.

References

[1] RAO S M, REDDY B V V, MUTTHARAM M. The impact of cyclic wetting and drying on the swelling behaviour of stabilized expansive soils[J]. Engineering Geology, 2001, 60: 223-233.

[2] Al-RAWAS A A, QAMARUDDIN M. Construction problems of engineering structures founded on expansive soils and rocks in northern Oman[J]. Building and Environment, 1998, 33: 159-171.

[3] POULOS H G, DAVIS E H. Pile Foundation Analysis and Design[M]. New York: John Wiley & Sons, 1980.

[4] XIAO Hong-bin, ZHANG Chun-an, HE Jie, et al. Experimental study on expansive soil-structure interaction and its sensitive analysis[J]. Journal of Central South University of Technology, 2007, 14(3): 425-430.

[5] POULOS H G. Piled rafts in swelling or consolidating soils[J]. J Geotech Engrg, 1993, 119: 374-380.

[6] MOHAMEDZEIN Y E-A, MOHAMED M G, ELSHARIEF A M. Finite element analysis of short piles in expansive soils[J]. Computers and Geotechnics, 1999, 24: 231-243.

[7] XU K J, POULOS H G. 3-D elastic analysis of vertical piles subjected to “passive” loadings[J]. Computers and Geotechnics, 2001, 28: 349-375.

[8] GAO Zhong, XIONG Zhong-ming. Study on the swelling shear of the calculation of piles in swelling soil[J]. Journal Xi’an University of Archstecture and Technology: Natural Science, 2003, 35(4): 412-415. (in Chinese)

[9] XIAO Hong-bin, ZHONG Hui-hong, WANG Yong-he. Analysis of pile’s load transfer in layered soils[J]. Journal of Central South University of Technology: Natural Science, 2003, 34(6): 687-690. (in Chinese)

[10] XIAO Hong-bin. Theoretical and application research on load transfer of vertically loading large diameter piles[D]. Changsha: School of Civil and Architectural Engineering, Central South University, 2005. (in Chinese)

[11] POOROOSHASB H B, ALAMGIR M, MIURA N. Negative skin friction on rigid and deformable piles[J]. Computers and Geotechnics, 1996, 18(2): 109-126.

[12] TU Yu-min, YU Hong-liang. Nonlinear analysis of negative pile[J]. China Journal of Highway and Transport, 2001, 14(1): 31-34. (in Chinese)

[13] XIAO Hong-bin, ZHONG Hui-hong, ZHANG Yi-jing, et al. Numerical iteration method for determining load-settlement relationship of a single pile[J]. Rock and Soil Mechanics, 2002, 23(10): 592-596. (in Chinese)

_____________________________

Foundation item: Projects(50378097, 50678177) supported by the National Natural Science Foundation of China

Received date: 2006-12-24; Accepted date: 2007-03-27

Corresponding author: FAN Zhen-hui, Doctoral candidate; Tel: +86-731-2654339; E-mail: fanzhenhui@126.com

(Edited by YANG Hua)