基于构造型神经网络的分类算法

刘 承 水

(北京城市学院 城市信息应用研究所，北京，100083)

摘  要：提出一种基于构造型神经网络的最大密度覆盖分类算法，以便更加有效地解决模式识别的问题。首先，引入一个密度估计函数，用该函数对样本数据进行聚类分析，找出同类样本中具有最大密度的样本数据点，然后，在特征空间里作超平面与球面相交，得到1个球面覆盖领域，从而将神经网络训练问题转化为点集覆盖问题。该算法的特点是直接对样本数据进行处理，有效地克服了传统神经网络训练时间长、学习复杂的问题，同时也考虑了神经网络规模的优化问题。计算机仿真实验结果证实了该算法的有效性。

关键词：模式识别；神经网络；覆盖；神经元；分类算法

中图分类号：TP18          文献标识码：A         文章编号：1672-7207(2009)03-0737-05

Classification algorithm based on constructive neural networks

LIU Cheng-shui

(Digital City Institute, Beijing City University, Beijing 100083, China)

Abstract: A new maximum density covering classification algorithm based on constructive neural networks was proposed, which can be used to resolve the problem of pattern recognition more effectively. Firstly, a density estimating function was proposed, which was used for clustering analysis of sample data, and a sample data point with the maximum density was found. Then, a super-plane was made to intersect a sphere in the characteristics of the space, and a spherical covering area was obtained, by which the training problem of neural networks can be transformed into the covering problem of a point set. The characteristic of the algorithm is that the sample data can be handled directly. This new algorithm can reduce the long training time and learning complexity of traditional neural networks. The optimization of the neural network is also considered. The simulation results show that the proposed neural network is quite efficient.

Keywords: pattern recognition; neural networks; covering; neuron; classification algorithm

模式识别自被提出以来，随着计算机的发展和人工智能技术的兴起，其理论和方法在很多科学和技术领域中得到了广泛的应用，并推动了人工智能系统的发展。模式识别使用的方法包括贝叶斯决策、统计方法、前馈神经网络等。前馈神经网络在求解模式识别问题时，其训练方法是基于预先给定的评价函数的极小化，用形式和数目预先确定的多个函数(即隐层单元的输出函数)的组合去逼近这一映射。这些方法都是从已知形式和数目函数的组合入手来分析。在现有的前馈神经网络算法基础上，宋宜斌等^[1]提出一种速率适应因子方法用于对多层前馈神经网络中BP算法进行改进；张海燕等^[2]提出了一种改进算法，该算法通过对权值调节量的修改，提高了网络训练过程效率。这些研究都是对网络算法进行一些调整和改进，但都没有从研究样本数据本身的角度来提出改进的方法。张铃等^[3-6]从样本数据本身出发，提出了一种新的M-P神经元的几何意义解释模型即“球领域”模型，从而，将神经网络的训练问题转化为求解“球领域”模型的最小几何覆盖问题。而求解球领域模型的最小几何覆盖问题是一个典型的NPC问题，目前，尚无有效的最优的求解方法。张铃等^[4]给出了一种求解该问题的次优方法即多层前向网络交叉覆盖设计算法，该算法通过反复迭代求取最优的“球领域”覆盖中心，使得球领域覆盖数最少。但是，该算法还存在以下不足：最终覆盖的质量受先验知识和初始种子样本的选择以及样本分布的影响较大；交叉覆盖算法虽然在某种意义上可以使得神经网络规模最小，但该算法相对复杂，实现比较困难。为此，本文作者从研究数据样本的角度出发，首先研究神经元的几何意义，以“球领域”模型为基础，提出一种新的基于最大密度“球领域”覆盖的多层神经网络训练算法。这个训练算法引入一个密度估计函数来确定未被覆盖样本的最大密度，依次得到一系列具有不同优先级别的“球领域”覆盖，在此基础上，进而通过神经网络的算法求出结果。

1  神经网络最大密度覆盖算法原理

1.1  神经元模型的几何意义

广义地，可将1个神经元理解为1个如下的基本运算^[7]：

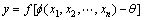。        (1)

如对于BP网络的神经元，其基本运算规则为：

因而，可以把一个神经元看成多维空间中的一个超平面，其表达式为：

而神经元输出函数f(?)的基可以看作是输入空间的输入点偏离该超平面的程度。

显然，超平面的几何概念有助于人们认识和分析神经网络行为。在基于神经网络的模式识别中，把每个神经元看作是在多维空间中的一个超平面，依次来划分输入空间的样本点。而若把先分离的某些样本点挖掉不再参加后面的划分，就像1只苹果中有许多不同颜色的污点一样，先靠边切1刀把若干个同一颜色的污点切掉，并把这切下的1片苹果拿走，依次一刀刀地切，总能把所有的各色污点分离在许多片被切下的苹果中。每切1片至少能切去1个或几个同色的污点。若每切1片都尽量切下最多的同颜色的污点，则可以实现以最少的切片把所有的污点去除。而对于较先切下去的切片，则赋予它较高的优先级别。

正是基于这一几何常识，本文作者提出一种基于空间最大密度覆盖的前向神经网络算法。该算法首先把样本点投影到一个超球面上，然后，在球面上找到同类样本密度最大的样本点，并以该样本点为中心作一超平面P与球面相交。这时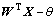，＞0就表示落在P的正半空间的部分，该部分恰好是球面上的某个“球形领域”，且它的中心就是W，并且把落入该“球形领域”的样本点去掉，不参加以后的运算。如此重复，每次在剩余的样本中寻找同类样本的密度最大的样本点，得到“球形领域”，并去掉落入其中的样本点，直到所有的样本点被覆盖为止，同时，把先得到的“球形领域”赋予较高的优先级别。因此，对球面上的点分类，只要构造若干球形领域，将它们都覆盖，在判断某一样本的类别时，只要看它被哪个优先权较高的球领域覆盖即可。

1.2  神经网络最大密度覆盖学习算法及其性能分析

给定一个训练样本集K={(X_{i, j}, y_i), 1≤i≤c, 1≤j≤N_i}(其中：c表示训练样本的类别数，N_i表示第i类样本的样本个数，X_{i, j}表示属于第i类第j个样本向量)，同时，y_i表示其输出的类别标志。首先，把所有的输入样本向量都投影到1个n维的球面上，即让模式空间中的所有点构成1个半球面，然后，根据这些点在球面上的位置进行聚类和识别。

定义1个变换T:D→Sⁿ, X∈D, T(X)=(X, 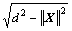)。其中D为n维模式空间，Sⁿ为n+1维空间的n维球面^[7]，d为一实数，且大于模式空间中所有向量的模的上界。这样，就把所有的训练样本都投影到1个超球面的正半球面上，训练样本仍然用集合K表示。

对于任一训练样本X_{i, j}，给出它在超球面上同类样本中的密度估计函数的定义：

这样，在半径r_{i, j}以外的样本向量对X_{i, j}的密度D_{i, j}几乎没有影响。显然，若1个训练样本有较大的密度，则其周围一定有较多的相同类别的样本点。

定义

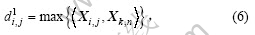
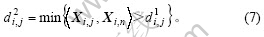
其中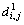：表示X_{i, j}与异类样本内积的最大值，即与异类样本的最近距离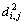；表示X_{i, j}与同类样本内积的最小值，即与同类样本的最远距离。它们都表示了训练样本间的相似度。

下面给出神经网络分类器的训练算法步骤。

a. 计算所有未被覆盖的样本数据点的密度D_{i, j}，求其最大值，得到具有最大密度的样本数据点X′。

b. 计算该样本数据点X′处的d¹和d²，求得d=    a×d¹+b×d²，其中，a和b为参数，且满足a+b=1。

c. 以样本点X′作为法向量W，d作为阈值θ作超平面：W^TX-θ=0，与球面相交。

d. 求出满足W^TX-θ＞0的样本点，把它们从训练样本中去掉，同时设置该“球形领域”的优先级别，原则是越先得到的“球形领域”对应的优先级别越高；返回至步骤a继续重复执行，直到所有的样本都被去掉为止。

因此，可以把神经网络分类器的设计问题转化为训练样本的覆盖问题，即用一组球领域去覆盖具有相同类别的训练样本，而不同类别的样本点被不同组的球领域覆盖。也就是1个神经元(W, θ)在几何意义上对应1个球领域。当1个样本落在球领域中，则神经元的输出为1；否则，输出为-1。1个神经元就充当    1个类别的鉴别器。球领域覆盖的个数就是神经网络分类器第1层所需神经元的个数。所有输入数据被第1层神经元分成不同的类别，而第2层神经元则给出输入数据的特定输出。

传统的神经网络具有以下2个缺点：首先，并没有理论来保证它一定收敛，而且学习复杂度也很高。其次，能否选择恰当的隐层节点数也是1个难题。使用神经网络覆盖算法能够克服传统神经网络的这2个不足。原因在于：首先，该算法是一种全新的算法，使用的是构造的方法，学习时间完全由覆盖时间决定，因此，不存在是否收敛的问题；其次，使用该算法，由于神经网络的隐层节点数完全由训练样本的球领域覆盖数决定，也就是说，隐层节点数的个数是可以控制的，若得到的覆盖数最少，则神经网络就具有最少的隐层节点数。

2  实验及结果

这里给出2个实验来证明所提出的最大密度覆盖学习算法的有效性。第1个实验采用与文献[8]中相同的实验数据，以便将本文提出的算法与文献[4]中的方法进行比较；在第2个实验中，对高维物体进行识别，以说明本文算法同样适用于高维模式的识别。

2.1  双螺旋线识别问题的实验

考虑平面上双螺旋线的识别问题。双螺旋线是由极坐标系统下方程r=θ和r=-θ (π/2≤θ≤6π)，这2条曲线互相缠绕而成，分别取78个点作为训练样本数据，θ=iπ/2, i=1, 2, …, 12，以及在区间π/2~π取二等分点，在π~3π/2取三等分点，一般在iπ/2~(i+1)π/2区间取(i+1)个等分点。Baum等^[8]试图利用BP算法求解双螺旋问题，但是没有成功；Chen等^[9]提出“生成-收缩”法，经过3 000次迭代运算，正确率只有89.6%；Fahlman等^[10-13]提出级联神经网络，使用超过10层神经网络来处理同一问题，但结果也不甚理想。可见，解决此问题的难度较大^[14-17]。

Clerc等^[14]在双螺旋线上随机各取10 000个点作为测试样本，输入所得到的网络进行识别，识别的正确率为98.245%，采用与文献[4]中同样的数据，并采用本文算法，正确率也达到98.2%。文献[4]中，当把训练样本随机增加到400个时，正确率最高为99.995%，而采用同样的检测样本，使用本文算法所得正确率达100%，见表1。

表1  不同算法的实验结果比较

Table 1  Comparison of experimental results using different algorithms

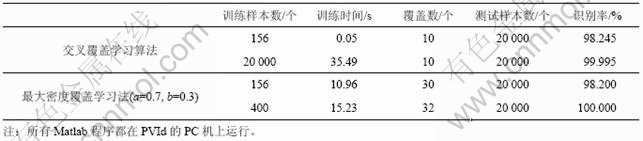
由表1可见，采用文献[4]中的算法所得的球领域覆盖数为10，即神经网络输入层神经元个数为10，而采用本文中的算法得到的覆盖数为30和32，大大多于文献[4]中所得的覆盖数。采用文献[4]中的算法得到的结果较好，因为它的算法是从中心样本点开始进行，所得到覆盖数较低。但若初始点选择不当，则采用文献[4]的算法就可能大大降低识别率。而采用本文的算法不受初始种子样本的影响，与初始点的选择无关，可以说本文算法的鲁棒性较好。所以，使用本文算法，可以通过增加训练样本数来提高样本识别的正确率。

2.2  图像识别实验

实验采用的是图像数据库COIL(Columbia object image library)，该数据库由100个物体以及每个物体水平旋转1周所采集的72幅图像(每幅图像水平角度相差5?)组成，每幅图像分辨率为128×128。

任意选取其中20个物体进行5次实验。每次实验时，随机选取每个物体的36幅图像作为训练样本，其余的图像作为检测样本。在图像空间中，每幅图像就是128×128维向量。为了减少运算量，首先采用主元分析对高维样本进行维数压缩，然后，利用本文算法进行识别。随着特征维数的增加，图像识别的平均错误率如图1所示。

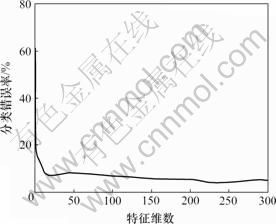
图1　分类错误率与特征维数的关系

Fig.1  Relationship between classification error rate and characteristics dimension

从图1可以看出，随着特征维数的增加，平均分类错误率迅速下降。当特征维数大于250时，分类结果趋于稳定，错误率最低可达3%。而且在每次实验中，神经网络的平均训练时间(即样本点覆盖时间)为56 s，这在传统神经网络训练中是不可能实现的，而且本文中构造的神经网络的识别正确率也较高。因此，本文算法也适用于高维模式识别问题。

3  结　论

a. 利用M-P神经元模型的几何意义提出1个基于构造型神经网络的最大密度覆盖学习算法，避免了传统BP神经网络存在的问题。通过分析神经网络规模的优化问题，构造“球形领域”来覆盖训练样本，从而将神经网络的训练问题转化为点集的覆盖问题，从数据本身出发逼近其分布的几何轮廓，表现出良好的分类性能。使用该算法分别对低维双螺旋曲线进行识别实验，与其他算法相比，表现了较好的鲁棒性。使用该算法对高维图像进行识别实验，逼近速度较快，识别率可达100%。

b. 该算法与传统的神经网络相比，具有训练时间短、正确率高等优点，有利于模式识别中基于构造型神经网络的改进。

参考文献：

[1] 宋宜斌, 王培进. 多层前馈神经网络改进算法及其应用[J]. 计算机工程, 2003, 29(14): 12-15.
SONG Yi-bin, WANG Pei-jin. An improved BP algorithm for FNN and its application[J]. Computer Engineering, 2003, 29(14): 12-15.

[2] 张海燕, 胡光锐, 张东红. 多层前向神经网络的一种改进BP算法[J]. 通信技术, 2003(11): 23-25.
ZHANG Hai-yan, HU Guang-rui, ZHANG Dong-hong. A new BP algorithm of multiplayer neural network[J]. Communications Technology, 2003(11): 23-25.

[3] 张 铃, 张 钹. M-P神经元模型的几何意义及其应用[J]. 软件学报, 1998, 9(5): 334-338.
ZHANG Ling, ZHANG Bo. A geometrical representation of M-Pneural model and its applications[J]. Journal of Software, 1998, 9(5): 334-338.

[4] 张 铃, 张 钹, 殷海风. 多层前向网络的交叉覆盖算法[J]. 软件学报, 1999, 10(7): 737-742.
ZHANG Ling, ZHANG Bo, Yin Hai-feng. An alternative covering design algorithm of multi-layer neural networks[J]. Journal of Software, 1999, 10(7): 737-742.

[5] 吴鸣锐, 张 钹. 一种用于大规模模式识别问题的神经网络算法[J]. 软件学报, 2001, 12(6): 851-855.
WU Ming-rui, ZHANG Bo. A neural network algorithm for large scale pattern recognition problems[J]. Journal of Software, 2001, 12(6): 851-855.

[6] 陶 品, 张 钹, 叶 榛. 构造型神经网络双交叉覆盖增量学习算法[J]. 软件学报, 2003, 14(2): 194-201.
TAO Pin, ZHANG Bo, YE Zhen. An incremental bicovering learning algorithm for constructive neural network[J]. Journal of Software, 2003, 14(2): 194-201.

[7] 王守觉, 王柏南.人工神经网络的多维空间几何分析及其理论[J]. 电子学报, 2002, 30(1): 1-4.
WANG Shou-jue, WANG Bai-nan. Analysis and theory of high-dimension space geometry for artificial neural networks[J]. Acta Electronic Sinica, 2002, 30(1): 1-4.

[8] Baum E B, Lang K J. Constructing hidden units using examples and queries[C]//Neural Information Processing. Lippman R P, et al, ed. San Mateo, CA: Morgan Kaufmann, 2003: 904-910.

[9] Chen Q C. Generating-shrinking algorithm for learning arbitrary classification[J]. Neural Networks, 2004, 5(7): 1477-1489.

[10] Fahlman S E, Lebiere C. The cascade-correlation learning architecture[J]. Advances in Neural Information Processing Systems, 2000, 2: 524-532.

[11] van Den B F, Engelbrecht A P. A cooperative approach to particle swarm optimization evolutionary computation[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 225-239.

[12] Gen M, Yun Y S. Soft computing approach for reliability optimization: State-of-the-art survey[J]. Reliability Engineering & System Safety, 2006, 91(9): 1008-1026.

[13] HE Qie, WANG Ling. An effective co-evolutionary particle swarm optimization for constrained engineering design problems[J]. Engineering Applications of Artificial Intelligence, 2007, 20(1): 89-99.

[14] Clerc M, Kennedy J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(1): 58-73.

[15] Ha C H, Kuo W. Reliability redundancy allocation: An improved realization for nonconvex nonlinear programming problems[J]. European Journal of Operational Research, 2006, 171(1): 24-38.

[16] 王英健, 戎丽霞. 基于遗传BP算法的神经网络及其在模式识别中的应用[J]. 长沙交通学院学报, 2005(1): 19-23.
WANG Ying-jian, RONG　Li-xia. Neural network based on GA-BP algorithm and its application in the pattern recognition[J]. Journal of Changsha Communications University, 2005(1): 19-23.

[17] 许延伟, 刘希玉. 神经网络用于模式识别的几种主要方法及比较[J]. 信息技术与信息化, 2005(4): 24-28.
XU Yan-wei, LIU Xi-yu. Several main methods and their comparison of neural network in pattern-recognition[J]. Information Technology & Informatization, 2005(4): 24-28.

收稿日期：2008-08-15；修回日期：2008-11-12

基金项目：国家自然科学基金资助项目(70671040)

通信作者：刘承水(1964-)，男，山东曲阜人，博士，副教授，从事城市管理、客户管理等研究；电话：010-62320646；E-mail: stream@bcu.edu.cn, stream168@163.com