DOI: 10.11817/j.issn.1672-7207.2018.01.012
考虑包辛格效应的辊式矫直截面反弯特性
马晓彬1，张杰1，李洪波1，周一中2，胡伟东2，张中伟2
(1. 北京科技大学 机械工程学院，北京，100083；
2. 宝钢股份武汉钢铁有限公司，湖北 武汉，430083)
摘要：基于弹塑性弯曲基本原理，以板材进入矫直机后经历的第2次弯曲为例，建立考虑包辛格效应影响程度(KBa)的辊式矫直复杂弯曲力学模型。采用该模型计算KBa对第2次弯曲时M-C关系和ξ-C关系及残余应力的影响，证明辊式矫直过程中经历多次弹塑性弯曲的截面反弯特性受材料包辛格效应的影响，而且随着材料强化系数的增大，截面弯曲特性所受影响越显著。最后计算相同矫直工况下，KBa不同的材料的残余曲率，得到材料KBa对于残余曲率的影响。研究结果表明：强化系数较大(η＞0.01)的材料进行矫直仿真时应考虑包辛格效应，在实际生产中确定工艺参数时需要首先确定材料的KBa。
关键词：包辛格效应；辊式矫直；强化系数；弯矩-曲率；残余应力
中图分类号：TG333.2 文献标志码：A 文章编号：1672-7207(2018)01-0087-08
Reverse bending behavior of section during roller leveling process considering Bauschinger effect
MA Xiaobin1, ZHANG Jie1, LI Hongbo1, ZHOU Yizhong2, HU Weidong2, ZHANG Zhongwei2
(1. School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China;
2. Baosteel Wuhan Iron & Steel Co. Ltd., Wuhan 430083, China)
Abstract: Based on the basic theory of elastic-plastic bending, a mechanical model of complicated bending process of the section under different degrees of Bauschinger effect (KBa) was built by taking the second bend of the plate bears after bited into the leveler as an example. The effect of KBa on the M-C and ξ-C relation and residual stress distribution could be gotten through the model calculation, which could prove that the reverse bending behavior of the elastic-plastic bending section, after experiencing several times of deformation during roller leveling process, was affected by the Bauschinger effect of the material. And more pronounced was gotten with the increase of the strength coefficient of the material. Finally, the residual curvatures of materials with different KBa under the same process conditions were calculated and the effect of KBa on it were gotten. The results show that the Bauschinger effect should be considered when roller leveling with the coefficient of the material is big(η＞0.01) and KBa of the material needs to be firstly determined when process parameters in actual production are determined.
Key words: Bauschinger effect; roller leveling; strength coefficient; moment-curvature; residual stress
辊式矫直是消除板材的弯曲或扭转变形，保证其几何精度的主要手段[1]，整个矫直过程是一个典型的多次连续弯曲的复杂弹塑性弯曲过程。板材在弯曲-反向弯曲变形过程中会受到包辛格效应的影响，其截面的后继屈服应力不断改变，导致弯曲后截面的应力分布发生变化[2]，影响反复弯曲过程中某次弯曲加载的弯曲力矩与弯曲量之间的关系(M-C关系)。针对辊式矫直过程，由于之前所矫直板材多为大韧性的普通钢种，屈服平台且矫直时最大塑性变形率较小(5εs左右，其中，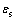
为屈服应变)，加载时可不考虑应变强化，故也无需考虑包辛格效应对材料后继屈服应力的影响，因此，国内外的研究大多基于理想弹塑性材料建立矫直分析模型[3-7]。但高强度钢板因其具有小韧性材料无屈服平台，材料强化特性明显，之前基于理想弹塑性材料的分析不能准确描述其矫直过程。针对强化材料，目前有学者在没有考虑包辛格效应的情况下分析强化材料截面在复杂弯曲过程中的弯曲特性[8]；也有学者只考虑材料某一极限情况下的包辛格效应，基于随动强化模型，建立了一组交变弯曲下压力和挠度曲线的拟合方程，确定复杂弯曲过程中的弯曲特性[9-10]。由于包辛格效应对材料的影响程度各不相同[11-12]，未考虑包辛格效应或只考虑单一影响程度下的包辛格效应并不能准确仿真分析不同品种钢板的矫直过程，不能通过计算得到不同品种强化材料板材矫直时所需的正确工艺参数，导致目前强化材料产品的矫直合格率较低。热轧横切线中矫直设备需要处理的高强钢品种多样，各品种所受的包辛格效应影响程度也不相同，为了更加准确地分析不同品种高强钢的辊式矫直过程，提高矫直仿真模型的精度，基于弹塑性基本原理，以板材进入矫直机后经历的第2次弯曲为研究对象，本文作者建立考虑包辛格效应影响程度(KBa)的辊式矫直复杂弯曲力学模型，重点分析矫直过程中复杂弹塑性弯曲过程中截面应力演变及M-C关系。根据分析结果得到包辛格效应影响程度不同带来的强化材料弯曲特性的改变，并讨论弯曲加载历史以及材料强化系数对包辛格效应的影响。最后整个矫直过程可以简化为板材连续通过数个弯曲单元，以该模型为基础，计算KBa不同的板材经过工艺参数相同的矫直，最终的出口残余曲率，得到最终的矫直分析结果。
1 材料性质与参数设定
1.1 包辛格效应及其强化模型
当强化材料正向加载到一定程度的塑性应变后，此时的应力称为正向后继屈服应力，它是材料卸载并重新正向加载时新的屈服应力；但是在卸载并按反向施加载荷后，其反向后继屈服应力的绝对值要比正向屈服应力下降，这种现象称为包辛格效应。描述材料在塑性加载—卸载—再加载过程中的应力应变关系的强化模型主要分为3类：各向同性强化、随动强化和混合强化。当强化材料的应力应变关系采用如式(1)所示的双线性强化模型描述，3种强化模型所描述的材料单向循环拉压时的单轴应力应变关系存在较大差别，如图1所示。
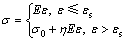
式中：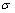
为应力；E为材料的弹性模量；
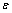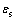为应变；为屈服应变；
为截距应力，等于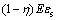
；η为材料的强化系数，
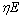等于塑性段直线斜率。
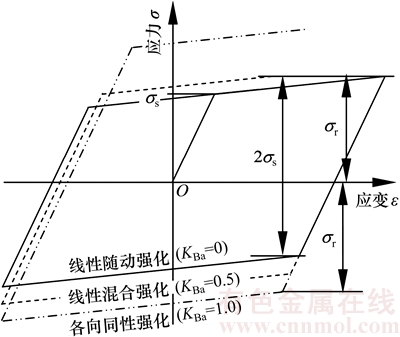
图1 3种强化模型的应力-应变关系
Fig. 1 Stress-strain relationship of three material hardening rule
从图1可以看出：各向同性强化不能体现包辛格效应，随动强化模型只能描述一种包辛格效应影响程度，而一般材料在复杂加载路径下不单纯表现为各向同性强化和随动强化，而是介于2种强化模型之间，是两者的结合，称为混合强化模型。
线性混合强化模型结合了各向同性强化和线性随动强化模型[13]，结构简单且能考虑不同影响程度的包辛格效应对强化材料弹塑性弯曲过程中后继屈服应力的影响，适用于考虑加载历史的强化材料的弹塑性弯曲研究。该模型将塑性应变增量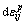
分为2部分：
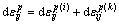
式中：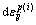
为与各向同性强化相关联的塑性应变增量，与屈服面的膨胀有关，
；
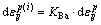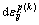与线性随动强化相关联的塑性应变增量，与屈服面的平移有关，
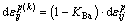；KBa为材料参数，表征包辛格效应影响程度，称为包辛格效应系数，取值范围为[0，1]。
由此可以得到正向加载后，反向后继屈服应力为
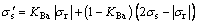
式中：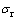
为加载方向变化时的应力；
为初始屈服应力；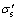
为后继屈服应力，其正负根据实际情况确定。
1.2 弯曲参数设定
利用弹塑性弯曲理论[14]对辊式矫直过程进行分析，为了简化分析过程，对弯曲过程中相关参数进行量纲一化。设矩形截面高度为H，弹性极限弯矩为Mt，弹性极限曲率角为At。弯曲时，截面弹性区高度为Ht，截面弯矩为M，弯曲曲率角为A。以这些参数为基础，进行如下定义：
1) 弯矩比为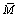
=M/Mt，反映截面弯矩；
2) 弹区比为ξ=Ht/H，反映截面塑性变形程度；
3) 曲率比为C=A/At=1/ξ，即弯曲过程中各种曲率角对弹性极限曲率角的比值，反映截面弯曲程度；
4) 相对高度为z=h/H，取值范围是[-1，1]，反映研究点的相对位置。
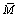，ξ和C是截面不同参数相对于其弹性极限状态的比值，由相对高度z描述的量纲一化矩形截面推导出的各种关系适用于任何矩形截面的强化金属材料。
2 考虑包辛格效应的反复弯曲分析
金属板带材在辊式矫直过程中经历的连续多次弹塑性弯曲可以分为简单弹塑性弯曲和复杂弹塑性弯曲。当完全不考虑(或不存在)弯曲截面的残余应力时，即为简单弹塑性弯曲，例如辊式矫直的第1次弯曲过程；在简单弹塑性弯曲基础上，再经过1次或多次弹塑性弯曲，即为复杂弹塑性弯曲，辊式矫直第2次及之后的弯曲就属于此列。以受包辛格效应影响的强化材料的辊式矫直过程中前2次弯曲为例，分析这2类弯曲过程中的截面应力分布、弯曲力矩、卸载后的应力分布和后继屈服应力分布等参数，确定2种情况下包辛格效应对截面弯曲特性的影响。
2.1 强化材料的简单弹塑性弯曲
崔甫等[1, 8]研究了强化材料简单弹塑性弯曲过程中的应力演化过程。设材料屈服应力为σs，强化系数为η，截面弯曲曲率比为C，则弯曲过程中沿高度z方向加载应力分布方程为
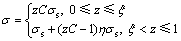
弯矩与曲率比的关系(即M-C关系)为
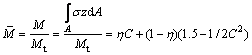
卸载后截面残余应力分布方程为
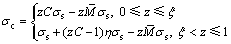
强化材料在简单弹塑性弯曲过程中截面应力演变过程如图2(a)和2(b)所示。由图2可知：截面应力分布的对称关系，因此，式(4)和式(6)中只列出了[0，1]区间的应力分布，[-1，0]区间的应力分布可由对称关系求得，文后列举的公式依照此方法。
强化材料截面在简单弹塑性弯曲过程中截面表层部分进入后继屈服过程，材料的包辛格效应导致板材截面表层在弯曲加载过程中后继屈服应力改变。板材截面加载方向的后继屈服应力由弯曲加载的最大应力确定；反方向的后继屈服应力则随KBa不同而变动，如图2(c)所示。图2(c)中阴影区即为由KBa决定的反方向后继屈服应力范围。
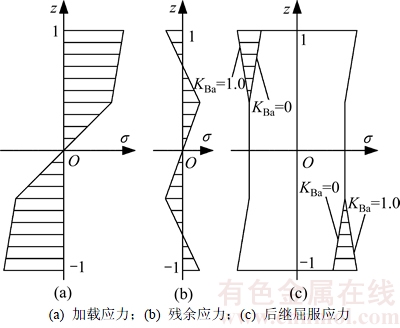
图2 截面应力演变与后继屈服应力
Fig. 2 Evolution of section stress and subsequent yield stress
板材截面后继屈服应力的改变，导致强化材料截面在后续弯曲加载过程中，截面不同高度处的进入屈服所需的应力发生改变，从而影响后一次弯曲过程中的M-C关系。
2.2 强化材料的第2次弹塑性弯曲
强化材料第2次弹塑性弯曲是复杂弹塑性弯曲中力学模型最简单的一种，通过对第2次弹塑性弯曲的推导，可以得到分析更高次复杂弹塑性弯曲的截面弯曲特性的基本原理与方法。设截面第1次正方向弯曲曲率比为C1，第2次反向弯曲曲率比为C2，分析强化材料的第2次弹塑性弯曲过程。
2.2.1 应力分布与弯矩
强化材料板材在第2次弯曲加载时，受前次弯曲残余应力和后继屈服应力的影响，截面应力分布形式比简单弹塑性弯曲时更为复杂，且不能通过简单的应力叠加获得。设第1次弯曲截面残余应力为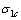
，根据平截面假设，第2次弯曲时各高度处的总应变
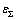为
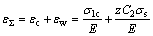
式中：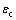
为上次弯曲的残余应变；
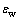为二次加载时弯曲应变，由于第2次弯曲曲率比按材料初始状态的材料参数计算，因此计算时采用初始屈服应力。
结合第1次弯曲卸载后截面不同高度的后继屈服应力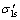
，判断该高度处是否屈服，进而计算屈服后的加载应力，确定第2次弯曲加载后的加载应力分布 
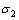为
结合式(7)和式(8)可知：第2次弯曲加载的应力分布可以根据C2的大小分成3种不同的形式，如图3所示。
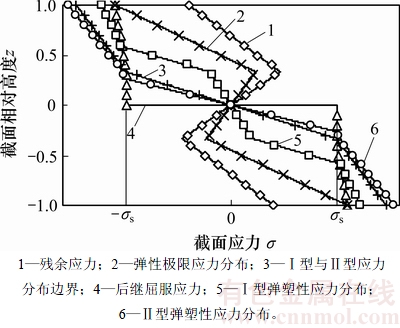
图3 第2次弯曲加载前后的应力分布
Fig. 3 Distribution of section stress before and after loading step of the second bending process
3种不同的应力分布方程及该情况下弯曲加载的弯矩方程如下。
1) 弹性应力分布。此时矩形板材截面各高度处尚未进入塑性变形阶段，将式(6)和式(7)代入式(8)可得该情况下的加载应力分布方程为
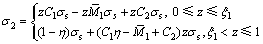
此时的弯矩比
为
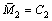
2) Ⅰ型弹塑性应力分布。该情况属于辊式矫直中后一道次压下量小，弯曲程度低，后一次弯曲加载时弯曲应力不能完全消除前一次弯曲加载留下的残余应力的影响。其加载应力被前后2次弯曲的弹区比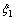
和
分割为5段。
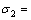
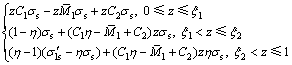
将截面应力对截面形心取矩，得到Ⅰ型应力分布时的弯矩比：
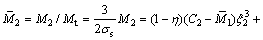
式中：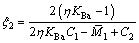
。
3) Ⅱ型弹塑性应力分布。该情况属于辊式矫直中后一道次压下量大，弯曲程度高，后一次弯曲加载的塑性应变范围超过前一次弯曲。其加载应力分布方程由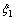和分割为5段，其中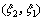
和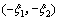
2区间内由于前一次弯曲时处于弹性范围内，其屈服应力仍然为初始屈服应力。
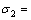
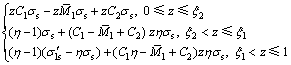
此时的弯矩比为
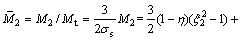
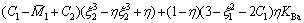
式中：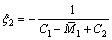
。
2.2.2 应力分布边界
由前面的推导可以看出：第2次弯曲加载后的应力分布形式以及对应的弯矩比、弹区比等均与第1次弯曲时不同，明晰第2次弯曲加载后3种应力分布的边界，确定第2次弯曲加载时的M-C关系，是分析包辛格效应对第2次弯曲加载影响的前提。
1) 弹性极限边界。由图3可知：当加载至弹性极限状态时，表层加载应力与表层的后继屈服应力相等，即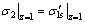
。联立式(3)和式(4)，可得z=1时的表层后继屈服应力为
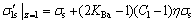
联立式(9)和式(15)，整理可得弹性极限边界方程为
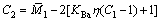
2) Ⅰ型与Ⅱ型应力分布边界。由图3可知：当加载至Ⅰ型与Ⅱ型应力分布分界时，弯曲加载的弹区比相等，即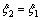
。在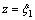
处，第1次弯曲时加载应力恰好等于，因此该点的后继屈服应力等于。根据式(11)可得Ⅰ型与Ⅱ型应力分布边界方程为
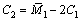
式(16)和式(17)所描述的边界将空间分割为3个区域，分别是弹性弯曲区、Ⅰ型应力分布区与Ⅱ型应力分布区，两边界如图4所示。
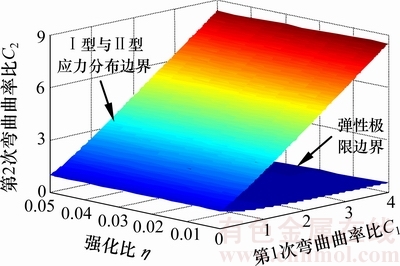
图4 第2次弯曲时的应力分布边界
Fig. 4 Boundary of section stress distribution during the second bending process
2.2.3 残余应力与后继屈服应力
根据弹塑性弯曲的弹性回复理论，弹性卸载的力矩与弯曲力矩相等，方向相反，则最终的残余应力分布为
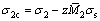
由于弹性加载阶段的加载应力与弹复应力相等，因此，第2次弹性加载的残余应力分布与未加载前的应力分布相同。对于Ⅰ型与Ⅱ型加载，结合式(11)~(14)和式(18)，就可以计算出2种情况下的残余应力分布函数，得到残余应力分布曲线，如图5所示。第2次弯曲卸载后的截面后继屈服应力可由加载应力分布和式(3)共同确定。
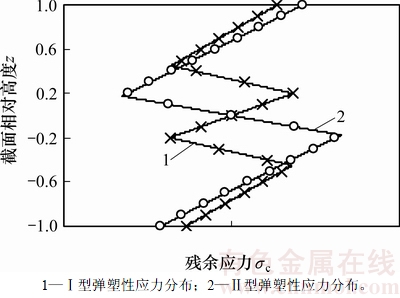
图5 第2次弯曲卸载后的残余应力
Fig. 5 Distribution of section residual stress after unloading step of the second bending process
3 包辛格效应对2次弯曲的影响
通过之前的推导，得到了第2次弯曲的加载应力分布形式，卸载后残余应力和后继屈服应力以及加载所需的弯矩。现通过上述方程分析第2次弯曲时KBa对截面弯曲特性的影响，以及η，C1和C2等参数的变化引起KBa的改变。
3.1 加载过程
弯曲加载时截面弹区比与弯曲曲率比的关系(ξ-C关系)和弯矩比方程(M-C关系)反映了该截面的弯曲特性。在矫直仿真计算中，ξ-C关系、M-C关系是否准确，决定了计算出的矫直机压下参数在实际生产应用中的效果。根据前面对第2次弯曲过程分析，由式(12)和式(16)得到KBa对弹区比和弹性极限曲率的影响，如图6所示。
从图6(a)可以看出：相同条件下，KBa不同时弹区比也不相同，而且在高强化系数、低弯曲曲率比的情况下，KBa不同引起的弹区比差别更大，如C2=1且强化系数较大(η=0.05)时ξ2相差17.03%，而强化系数较小(η=0.01)时仅相差2.87%。同样从图6(b)也可以看到：强化系数越高，KBa引起的弹性极限曲率比差值越显著，当η增加到0.05时，不同KBa下的弹性极限曲率比差值可达43.08%，即使η=0.01，差值也有16.50%。由以上分析可以看出：材料的包辛格效应影响程度不同，第2次弯曲时ξ-C关系和弹性极限曲率也会随之改变，当材料强化系数较高且第2次弯曲曲率比较小时，KBa对ξ-C关系和弹性极限曲率的影响越大。
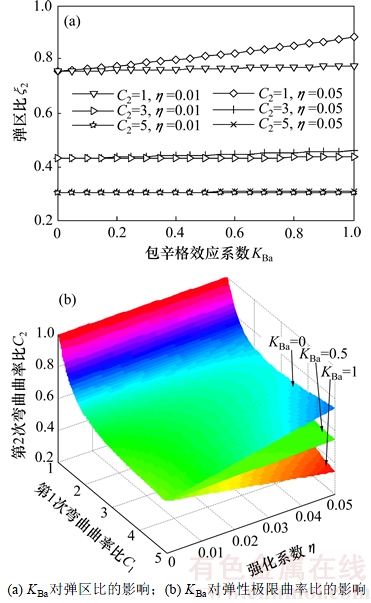
图6 KBa对弹区比和弹性极限曲率比的影响
Fig. 6 Effect of KBa on elastic region ratio and elastic limit curvature ratio
由式(12)和式(14)可以得到不同情况下KBa对第2次弯曲过程中M-C关系的影响，如图7所示。
由图7可知：C1和η越大，KBa的变化引起的第2次弯曲过程中M-C关系的变化越显著，如C1=5，η=0.05时，C2在(1，5)区间内的第2次弯曲弯矩比平均差值达到24.92%，最大差值达到26.52%。
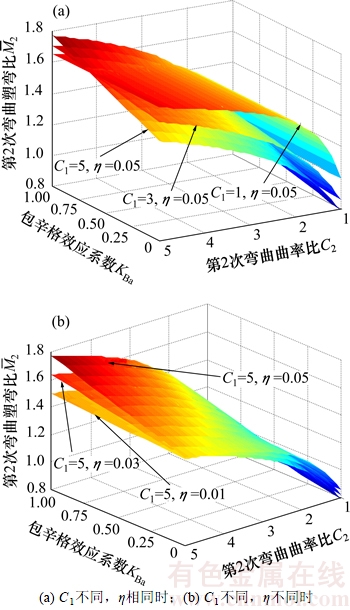
图7 KBa对第2次弯曲M-C关系的影响
Fig. 7 Effect of KBa on M-C relationship during the second bending process
由以上分析可以看出：在材料属性和弯曲参数确定的情况下，第2次弯曲的截面更易于进入塑性变形；在大强化系数、小弯曲曲率比的情况下，KBa变化引起ξ2的变化量更大，由于矫直机出口段矫直辊压下量小，对板材施加的弯曲曲率比小，KBa不同的材料经过矫直后的残余应力分布会发生显著改变。第2次弯曲时相同的曲率比所需要的弯矩相对简单弯曲时更小，这意味着第2次弯曲的弹复应力更小，因此，在实际辊式矫直过程中，不能只根据经典矫直理论设定矫直参数，要充分考虑2次及更高次弯曲时M-C关系的改变以及其对弹复后残余曲率的影响，即要达到同样的残余曲率要求，相较于经典理论应减小弯矩，即在实际生产中适当减小压下量。
3.2 卸载过程
弯曲卸载时主要关注截面内剩余的残余应力的分布情况及其大小，根据2.2.3节所述的第2次弯曲卸载残余应力计算方法，设σs=500 MPa，η=0.05，C1=3，C2和KBa分别取不同的值，计算第2次弯曲的残余应力。
图8所示为Ⅰ型与Ⅱ型2种应力分布的情况下卸载后的残余应力。从图8可知：在相同条件下，KBa变化引起的残余应力分布形式和峰值的变化很小，最大峰值应力差仅为12.33%(C2=3时)；而最大表层应力差出现在C2=1时，相对差值为158.02%，表明C2较小时KBa的影响更大。在C2逐渐增加的过程中，残余应力峰值有一个先减小后增加的过程，这要求在辊式过程中需要合适的压弯量以实现较小的残余应力。
当其他弯曲参数相同，η=0.01的材料第2次弯曲的残余应力峰值对于KBa的变化更加不敏感，最大峰值应力差仅为2.12%(C2=3时)；而最大表层应力差为21.66%(C2=1时)。
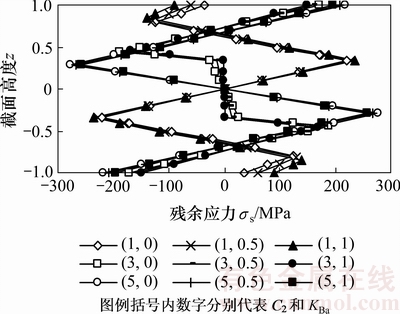
图8 KBa对第2次弯曲残余应力的影响
Fig. 8 Effect of KBa on distribution of section residual stress after unloading step of the second bending process
4 包辛格效应对高次弯曲的影响
在实际的辊式矫直过程中，金属板材各截面最终要经历3次以上的弹塑性连续弯曲过程。参考以上对2次反弯的弹塑性解析可知：随着截面上弯曲次数的增加，截面应力分布方程和后继屈服应力愈加复杂。采用解析的方法求解较为困难，根据上述第2次反弯过程的分析流程，采用合理的数值计算方法可以更加简单、快捷地解决问题。
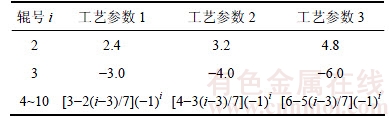
板材的截面反弯特性在经历弹塑性弯曲之后，由于包辛格效应的影响而产生改变，为了分析截面反弯特性的改变对板材矫直过程的影响，总结不同KBa的板材经历相同的弯曲历史后的残余曲率，以某11辊矫直机为例，根据前述弹塑性弯曲分析过程，以数值计算的方法进行分析。设矩形金属板材最大截面初始曲率C0max=±3.0(使钢板凹向下的弯曲为正)，各截面初始曲率在该板材上随机连续分布；σ0.2=724.09 MPa，E=194.7 GPa，η=0.013 4。设定3组基于大应变原则的整体倾斜压下弯曲工艺参数Cw如表1所示。矫直机入口和出口处的第1辊和第11辊处的弯曲曲率均为0。
表1 第i辊处的设定弯曲曲率Cwi
Table 1 Bending curvature of set value (Cwi) on the ith roller
卸载后的截面残余应力、残余曲率和后继屈服应力作为初始状态，结合该次弯曲曲率Cwi就可以计算该次弯曲后的截面应力分布，从而得到弯曲力矩，进而计算出残余曲率、残余应力和后继屈服应力等参数。依照该流程，逐道次计算，即可得到材料KBa对于矫直出口残余曲率的影响，如图9所示。
图9所示为在不同的压下方案中，材料KBa不同时对其矫直出口残余应力的影响。从图9可知：增加矫直过程中的Cw可以有效降低板材的出口残余曲率，但是，随着Cw增大，增加Cw产生的出口残余曲率减小的效果逐渐下降；在KBa由0增加到1的过程中，出口残余曲率有一个先减小而后平稳最后减小的过程，KBa处于[0,0.2]和[0.9,1]这2个区间时，板材的出口残余曲率受到KBa的很大影响，因此，在矫直生产中，需要首先确定板材受到的包辛格效应，并据此设定合理的矫直工艺参数，以获得板形质量合格的板材。
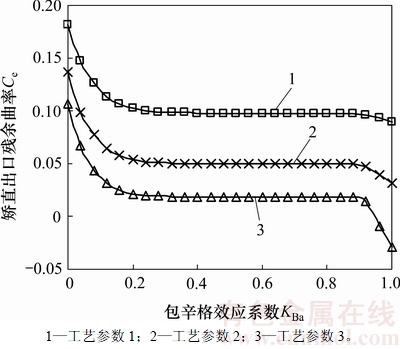
图9 KBa对矫直出口残余曲率的影响
Fig. 9 Effect of KBa on residual curvature at leveling exit
5 结论
1) 考虑材料的包辛格效应，重点分析了强化材料板材在矫直过程中的第2次弯曲过程，得到了弯曲过程中截面加载应力分布、残余应力分布、后继屈服应力分布、M-C关系和ξ-C关系等关于KBa的方程。
2) KBa不同的强化材料在弯曲过程中的ξ-C关系和M-C关系也不相同，材料的强化系数以及弯曲加载历史都会改变KBa变化所产生的影响。
3) 第2次弯曲产生的残余应力的峰值受KBa影响较小，表层残余应力在第2次弯曲曲率比较小时受KBa改变的影响较大，较大的强化系数会增强KBa改变时对残余应力的影响。
4) 强化系数较大(η＞0.01)的强化材料采用辊式矫直方式矫直时，材料的KBa不同导致最终矫直出口残余曲率不同，因此，对多次连续反弯的辊式矫直过程进行仿真分析时需要考虑材料的包辛格效应，并采用相应的KBa进行计算。
参考文献：
[1] 崔甫. 矫直原理与矫直机械[M]. 北京: 冶金工业出版社, 2005: 1-60.
CUI Fu. Straightening and straightening machine[M]. Beijing：Metallurgical Industry Press, 2005: 1-60.
[2] HAN K, TYNE C J V, LEVY B S. Effect of strain and strain rate on the Bauschinger effect response of three different steels[J]. Metallurgical and Materials Transactions A, 2005, 36(9): 2379-2384.
[3] CHEN Min, JIANG Xiaomin, ZHAO Zuxin. Innovation in the computing system of straightening force[J]. Chinese Journal of Mechanical Engineering, 2010, 23(1): 115-121.
[4] SCHLEINZER G, FISCHER F D. Residual stress formation during the roller straightening of railway rails[J]. International Journal of Mechanical Science, 2001, 43(10): 2281-2295.
[5] CHEN Weihua, LIU Juan, Cui Zhenshan, et al. A 2.5-dimensional analytical model of cold leveling for plates with transverse wave defects[J]. Journal of Iron and Steel Research, International, 2015, 22(8): 664-671.
[6] LIU Zhifang, LUO Yuanxin, YAN Xingchun, et al. Boundary determination of leveling capacity for plate roller leveler based on curvature integration method[J]. Journal of Central South University, 2015, 22(12): 4608-4615.
[7] 管奔, 臧勇, 逄晓男, 等. 矫直过程截面复杂反弯的应力分布与反弯特性解析[J]. 中南大学学报(自然科学版), 2012, 43(5): 1739-1745.
GUAN Ben, ZANG Yong, PANG Xiaonan, et al. Stress distribution and reverse bending behavior of section during roller leveling process [J]. Journal of Central South University(Science and Technology), 2012, 43(5): 1739-1745.
[8] 刘东冶, 何安瑞, 王海滨, 等. 塑性强化材料矫直反弯特性研究[J]. 机械工程学报, 2015, 51(8): 76-83.
LIU Dongye, HE Anrui, WANG Haibin, et al. Reverse bending research of leveling on plastic hardening material[J]. Journal of Mechanical Engineering, 2015, 51(8): 76-83.
[9] SEO J H, TYNE C J V, MOON Y H. Effect of roll configuration on the leveling effectiveness of tail-up bent plate using finite-element analysis[J]. Journal of Manufacturing Science and Engineering, 2016, 138(7): 071004.1-071004.7.
[10] 杨海波, 汪家才, 王卫平. 重轨矫直过程应力应变模型的确定与分析[J]. 北京科技大学学报, 1997, 19(增刊): 104-108.
YANG Haibo, WANG Jiacai, WANG Werping. Determination of relationship between stress and strain and analysis of mechanical property in rail straightening[J]. Journal of University of Science and Technology Beijing, 1997, 19(Suppl): 104-108.
[11] SILVESTRE E, MENDIGUREN J, GALDOS L, et al. Comparison of the hardening behavior of different steel families: from mild and stainless steel to advanced high strength steels[J]. International Journal of Mechanical Science, 2015, 101/102(4): 10-20.
[12] 庄京彪, 刘迪辉, 李光耀. 基于包辛格效应的回弹仿真分析[J]. 机械工程学报, 2013, 49(22): 84-90.
ZHUANG Jingbiao, LIU Dihui, LI Guangyao. Analysis of springback simulation based on Bauschinger effect[J]. Journal of Mechanical Engineering, 2013, 49(22): 84-90.
[13] HODGE P G. Discussion of the Prager hardening law[J]. ASME J. Appl. Mech., 1957, 24: 482-484.
[14] 赵军, 殷璟, 马瑞, 等. 小曲率平面弯曲弹复方程[J]. 中国科学：技术科学, 2011, 41(10): 1342-1352.
ZHAO Jun, YIN Jing, MA Rui, et al. Springback equation of small curvature plane bending[J]. Science China Technological Sciences, 2011, 41(10): 1342-1352.
(编辑 杨幼平)
收稿日期：2016-12-27；修回日期：2017-02-29
基金项目(Foundation item)：国家“十二五”科技支撑计划项目(2015BAF30B01) (Project(2015BAF30B01) supported by the National Key Technology R&D Program of the 12th Five-Year Plan of China)
通信作者：张杰，博士，教授，从事板带轧制技术与装备研究；E-mail: zhangjie@ustb.edu.cn
