Constitutive model of rock under static-dynamic coupling loading and experimental investigation

LI Xi-bing(李夕兵), ZUO Yu-jun(左宇军), WANG Wei-hua(王卫华),

MA Chun-de(马春德), ZHOU Zi-long(周子龙)

School of Resources and Safety Engineering, Central South University, Changsha 410083, China

Received 20 April 2005; accepted 8 September 2005

Abstract: The importance of study on constitutive model of statically loaded rock experiencing dynamic load is set forth, and the studying methods on dynamic constitutive model are classified according to the current studying status. By way of combining statistic damage model and viscoelastic model, uni-axial and multi-axial constitutive models of statically loaded rock experiencing dynamic load (static-dynamic coupling constitutive model) under intermediate strain rate are established. The verification experiment on 2D constitutive model under different static stress and dynamic stress with different frequencies is designed and performed. It is found that there is a good agreement between the experimental stress-strain curves and the theoretical stress-strain curves.

Key words：dynamic load; static-dynamical coupling loading; intermediate strain rate; constitutive model; damage; viscoelasticity

1 Introduction

Rock fragmentation, boring, explosive, rockburst etc in engineering domain of mineral are almost concerned with cracking of rock experiencing dynamic loading, and a plenty of results have been obtained[1]. But the related studies are almost limited to the case that rock undergoes dynamic load completely. In fact, a quite number of rocks in engineering practice, for example in excavating of mineral, have been on the state of bearing static stress or ground stress before rocks undergo dynamic load. However, the study on influence of static stress on the properties of deformation and fragmentation of rock experiencing dynamic load is deficient. So the study on the constitutive properties and fragmentation rule of rock undergoing coupled static-dynamic load should be attached importance to.

At present in the domain of rock mechanics, the studies on rock experiencing either static load only or dynamic load only have made great progress[2-16]. But there is very few studies on rock experiencing static-dynamic load until now[17-20], and in special, there is little literature[21-25] concerning rock under static-dynamic coupling loading at the same direction, and the same taking different confining pressure into account under static-dynamic coupling loading at the same direction. The literature is mostly about studies on failure and fracture of rock under static-dynamic coupling loading and the study on 1D and 3D constitutive model of rock under static-dynamic coupling loading.

Meanwhile there are many experiments and theoretic analyses on static constitutive relation of rock at low strain rate  (＜10^-4/s) and constitutive equation for rock at high strain rate (＞10²/s), but few between both rates above because of limitation of experimental conditions and technique[19].

The studies in the past indicate that the dynamic constitutive model of rock is the basic parameter to analyze the response of rock mass to dynamic loading[26-31]. The deformation of material such as rock is not only related with the state of stress, but also related with loading rate[32-37].

The studies on constitutive equations considering the effect of strain rate may be sorted into four kinds.

1) Experience and half-experience model[38-40]. Those based upon the rule deduced from experiment or combination of experiment and some theoretic analysis belong to this sort. Because of the complexity of rock properties and the brevity of dynamic loading, only a few of them are recognized as theoretic analysis results.

2) Mechanical model[41-42]. Properties of rock material undergoing uniaxial dynamic load are quite similar to that of model composing of elastic components and viscoelastic components according to certain regulation, so it is possible to establish differential dynamic constitutive equation of rock material undergoing dynamic load and whose coefficients are determined by test. The representative model should be excessive-stress model. Although this kind of model is able to represent the effect of strain rate, it is impossible to explain the effect of strain rate to strength, furthermore it is impossible to express the relation between stress and strain after peak value of stress.

3) Damage model. Damage model includes describing relation of stress and strain by way of macro theory and meso theory[43]. The macro theory model based on continuum damage mechanics defines damage variable using a vector, scalar quantity or tensor, then establishes macro constitutive model of material by way of damage variable. Although the model based on macro theory is able to express complete stress-strain curve, the effect of strain rate of rock deformation can’t be expressed, and it isn’t still solved that how many parameters should be used to describe the damage state of certain point, furthermore, it is questionable that how to determine the evolution law of damage variable. Meso theory describes forming core, propagation and converging of micro crack using related theory such as damage fracture mechanics, meso theory and fractal and expresses the change of macro mechanical properties by the same way mentioned just now[44].

4) Combination model[32,37, 45-47]. According to the deformation properties of rock, the above methods are combined to describe the deformation rule of rock. This sort of model is able to express the true deformation properties of rock, so it is often used.

There is a good agreement between the experimental data and the theoretical constitutive curve in literature[35] adopting the combination model, but the theoretical constitutive curve isn’t able to represent the influence of the primitive rock’s stress state, that is, it can’t describe the deformation properties of rock under static-dynamic coupling loading. So, the combination model established by Ref.[35] is also used in this study to discuss the deformation rule of two-dimensional statically loaded rock experiencing dynamic loading of

medium strain rate.

2 Constitutive model of statically and dyna- mically coupling loaded rock

2.1 Basic hypothesis

1) Inertia effect is neglectable under medium rate[1].

2) Rock occupies the characteristics of both statistical damage and visco-liquid, and may be regarded as a combination of damage mass D_a and visco-piston η_b, illustrated as Fig.1.

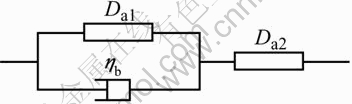
Fig.1 Rock unit model

3) Damage mass D_a characterizes isotropy of damage, linear elasticity before damage, whose average elastic module is E, whose strength is obedient to the statistical distribution with parameters (m, α). The damage variable D may be expressed as the following two types according to the stress state of rock:

For 1D loading[32, 48]:

 (ε_a≥0)    (1a)

For 2D and 3D loading[37, 49]:

 (ε_a≥0)               (1b)

Constitutive relation σ—ε may be expressed as

 (ε_a≥0)                     (2)

4) Visco-piston is without properties of damage, which is obedient to the constitutive relation:

                               (3)

5) Element mass is viscoelastic mass before damage.

6) The relation between stress σ and strain ε is obedient to linear differential equation, and the superposition principle of strain is available[41,42].

7) The constitutive equation may be obtained according to equivalent principle of strain.

2.2 Constitutive model of uniaxial statically loaded rock subjected dynamic load

The relation between stress and strain of combination mass is obedient to

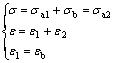                          (4)

Put the constitutive relation of damage mass and visco-piston into Eqn.(4), get the constitutive relation of combination:

                     (5)

It is found from Eqn.(5) that the damage constitutive relation may be gotten from viscoelastic constitutive relation by substituting the elastic module E of damage mass before damage with available elastic module E(1-D).

In order to evaluate Eqn.(5), don’t consider the properties of damage first. According to Eqn.(5), get the viscoelastic constitutive equation of combination mass as

                (6)

Suppose that at the beginning of dynamic load t=0, because rock undergoes static load, the state of stress isn’t naught, viz when t=0, ε(0)= ε₀, σ(0)=S. Considering the first state, by LAPLACE transformation get

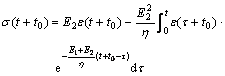     (7)

where  t₀ is time at which the stress state of rock is naught, and the static stress begins to load, here ( is the time tending towards t₀ in direction of less t₀).

If ε(t+t₀)=ε₀+ε_r(t)=ε₀+ct(c is the rate of strain, that is constant), according to Eqn.(7) get

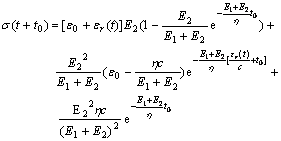        (8)

Substitute E₁ and E₂ in Eqn.(8) with E₁[1-D(t+t₀)] and E₂[1-D(t+t₀)], according to Eqn.(1a), D(t+t₀) is

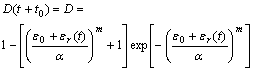       (9)

Then get uniaxial constitutive equation of isotropy damage mass undergoing static-dynamic coupling load:

(10)

In the above equations, according to analysis of experimental data and operation of theoretical constitutive model, it is found that the value of E₁ may be replaced by elastic module E_q of rock experiencing static load because E₁ is approximately equal to E_q; the value of E₂ may be replaced by linear elastic module E_qd of rock experiencing static-dynamic coupling loading at different strain rates because E₂ is approximately equal to E_qd; m is the form coefficient of the distribution curve of probability which is about 4-6;  is the complete strain corresponding to peak stress; η ranges from 0 to  1 000 GPa?s, furthermore, it hasn’t influence on the stress-strain curve choosing any value of η above; t₀ is the tested time duration of static loading; ε_r(t) is the strain caused by static-dynamic coupling loading; ε₀ is the initial strain caused by imaginational value S of the static-dynamic coupling load, if σ(t+t₀)=σ₀+σ_t, according to the initial condition, from Eqn.(8) get

σ(0)=σ₀=S=ε₀E₂                                             (11)

ε₀=S/E_qd                                    (12)

There are two purposes using the initial strain caused by imaginational static-dynamic coupling load S to substitute the true strain: 1) make the beginning point of stress-strain curve and static load S be superposition; 2) reduce the effect of elastic strain on damage during calculation. To do it in this way makes the fitting stress-strain curve to be more alike to experimental curve.

In a word, carrying through the numerical operation of the model above, five parameters , E₁, E₂, m, α, η are needed to be determined, by analyzing the tested data, and even by trial calculation. The tested data of strain ε_r(t), strain rate c and initial t₀ should be used.

When ε₀=t, t₀=0, Eqn.(10) may represent the constitutive relation of rock undergoing uniaxial dynamic load, here

          (13)

2.3 Constitutive model of rock subjected to triaxial static-dynamic coupling loading

1) Constitutive relation of unit mass before damage

According to hypothesis (5), the stress-strain relation of a 3D rock mass may be expressed as[42, 50]:

S_ij=2Ge_ij                                   (14)

σ_m=3Kε_m                                   (15)

where  S_ij is partial tensor of stress, the relation between S_ij, stress tensor σ_ij and spherical stress tensor σ_m is

σ_ij=S_ij+δ_ijσ_m                                 (16)

where  e_ij is partial tensor of strain, the relation between e_ij, strain tensor ε_ij and spherical strain tensor ε_m is

ε_ij=e_ij+δ_ijε_m                                 (17)

where  δ_ij is the sign of DIRAC; G is shear module; K is volume module.

According to hypothesis (6), the constitutive relation of viscoelastic mass may be expressed as the common format as follows[42]:

                             (18)

where  f(d) and g(d) are the multinomials of d and d is the differential coefficient of time.

The extending of Eqn.(18) to tri-axis is to substitute Eqn.(14) and Eqn.(15) as follows

　                       (19)

　                      (20)

where  f(d) and g(d) are related with aberration; f₁(d), and g₁(d) are related with hydrostatic stress.

Eqn.(19) and Eqn.(20) are the linear constant differential coefficient equations that must be solved coupling with stress balance equations and boundary conditions.

According to the above principle, the 3D constitutive equation of viscoelastic mass undergoing static-dynamic coupling loading is derived as follows[25]:

     (21)

Thereinto

　                   (22)

　　                (23)

                         (24)

When S_x0=0 or S_y0=0, the 3D constitutive equation above may be expressed as the constitutive relation of two dimension statically loaded rock undergoing dynamic load.

When S_x0=S_y0=S_z0, the 3D constitutive equation above may be expressed as the constitutive relation of triaxial dynamically loaded rock during confining pressure is loaded by triaxial experimental machine.

2) Constitutive relation of unit mass after damage

The fragmentation format of rock behaves commonly shear yield under condition of triaxial stress. According to Ref.[51], suppose that the fragmentation of unit mass complies to COULOMB criterion. On the basis of it, according to Eqns.(1) and (2) the damage variable of rock under 3D static-dynamic coupling loading may be expressed as follows referring to the damage variable determined by Ref.[49]:

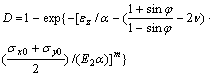      (25)

where φ, υ is interior friction angle and POSSION’s ratio respectively, the meaning of other signs are the same as before.

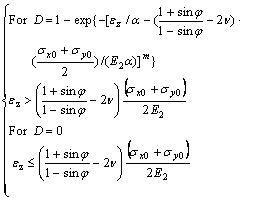  (26)

According to hypothesis (7), Lemaitre principle of strain equivalent is applicable. Applying Eqn.(26) to Eqns.(21)-(24) in which E₁, E₂ and K are substituted by E₁[1-D(t+t₀)], E₂[1-D(t+t₀)] and K[1-D(t+t₀)] respec- tively, isotropy 3D damage constitutive equation of viscoelastic material under static-dynamic coupling loading. Hereinto, D(t+t₀) is

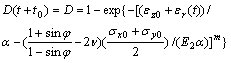      (27)

Determining the constitutive relation of two dimension statically loaded rock under dynamic load, Eqns.(25)-(27) are applicable.

In the above equations, E₁ is the elastic module of rock experiencing static load, E₂ is the linear elastic module of stress-strain curve of rock experiencing static-dynamic coupling load at average strain rate c; it is found by referring to Refs.[32,37] and trial calculation that m is the form coefficient of the distribution curve of probability which is about 5-20 for 2D, about 0.5-1 for 3D; α is the complete strain corresponding to peak stress; η is the visco-coefficient which about 1000 for 2D, ranging from 0-1 000 GPa?s for 3D, furthermore, it increases with increase of the average strain rate c; t₀ is the tested value of static loading duration; ε_r(t) is the strain caused by static-dynamic coupling loading; ε_z0 is the initial strain caused by imaginational value S_x0, S_y0, S_z0 that are static-dynamic coupling loads; σ_z(t+t₀) is the static-dynamic coupling stress when t≠0; interior friction angle φ and POSSION’s ratio υ are determined by test, volume module K is obtained according to equation K=E₂/3(1-2υ).

In a word, compared with the uniaxial constitutive equation, besides 5 parameters , E₁, E₂, m, α and η, 3 parameters , interior friction angle φ and POSSION’s ratio υ and volume module K need to be determined if the 2D and 3D constitutive equations need to be determined. The determination method of other parameters is the same as the uniaxial constitutive equation.

3 Experimental verification

The verification experiment of rock under 2D static-dynamic coupling load was done by way of low cycle fatigue loading. Red sandstone is used as specimen material, whose elastic module E₁=3.34 GPa, interior friction angle φ=60?, visco-coefficient η=1 000 GPa?s. The experimental equipment is made up of Instron 1342 electro-servo controlled testing system and horizontal static pressure loading device made by ourselves and shown as Fig.2. The constitutive relation of red sandstone experiencing 2D static-dynamic coupling load was studied under different horizontal static pressures and different vertical static pressures and dynamic loads of different frequencies. The results are shown in Figs.3-5 respectively(the 0 point of strain is that of static load and dynamic load to couple, the deformation of static load is not recorded).

Fig.2 Horizontal static pressure loading device: 1 Sample;    2 Vertical loading device of Instron 1342; 3 Hydraulic system of device; 4 Horizontal loading box; 5 Vertical loading device of Instron 1342

Fig.3 shows the experimental and theoretical stress—strain curves of red sandstone under 2D static-dynamic coupling loading with invariable vertical static stresses of 12 MPa, and different horizontal static stresses of 0, 2, 4, 6, 8 MPa respectively. It is found from Fig.3 that there is disturbance near the peak value of stress of tested stress—strain curves, which is caused by shearing and sliding of rock and isn’t able to be expressed using theoretical stress—strain curves; the value of elastic module of theoretical stress—strain curves are commonly little more than that of experimental stress—strain curves; with the increase of static stress, the theoretical stress—strain curves after peak values of stress move commonly to left because of shearing and sliding; after peak values of stress of curves, tested curves change largely, theoretical curves are more smooth.

Fig.4 shows the experimental and theoretical stress-strain curves of red sandstone under 2D static-dynamic coupling loading with invariable horizontal static stress of 8 MPa and vertical static stress of 12 MPa, and different dynamic load frequencies of 0.1, 0.5, 1.0, 1.5, 2.0 Hz respectively. It is found from Fig.5 that there is disturbance near the peak value of stress of tested stress—strain curves, and isn’t able to be expressed using theoretical stress-strain curves; also, the value of elastic module of theoretical stress—strain curves are commonly little more than that of experimental stress-strain curves; the peak values of stress of the experimental and theoretical stress—strain curves are approximately equal; after peak values of stress of curves, tested curves change largely, theoretical curves are more smooth.

Fig.5 shows the experimental and theoretical stress-strain curves of red sandstone under 2D static-dynamic coupling loading with invariable horizontal static stress of 8 MPa, and different vertical static stresses of 6, 12, 18, 24 MPa respectively. It is found from Fig.5 that there is larger disturbance near the peak value of stress of tested stress—strain curves, which is caused by shearing and sliding of rock and isn’t able to be expressed using theoretical stress—strain curves; because of shearing and sliding, the theoretical stress-strain curves move commonly to left, in order to decrease error, the average values of strain corresponding to that of shearing and sliding should be used as the fitting parameter α of theoretical constitutive curves; also, the value of elastic module of theoretical stress-strain curves are commonly little more than that of experimental stress—strain curves; the peak values of the stress of the experimental and theoretical stress-strain curves are approximately equal; after peak values of stress of curves, tested curves change largely, theoretical curves are more smooth.

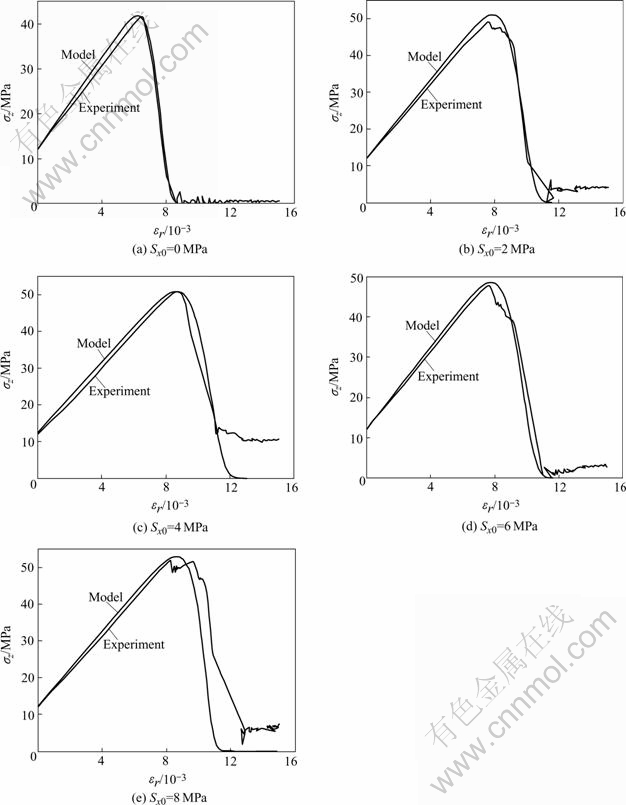
Fig.3 Experimental and theoretical 2D stress-strain curves of red sandstone experiencing different horizontal static stresses

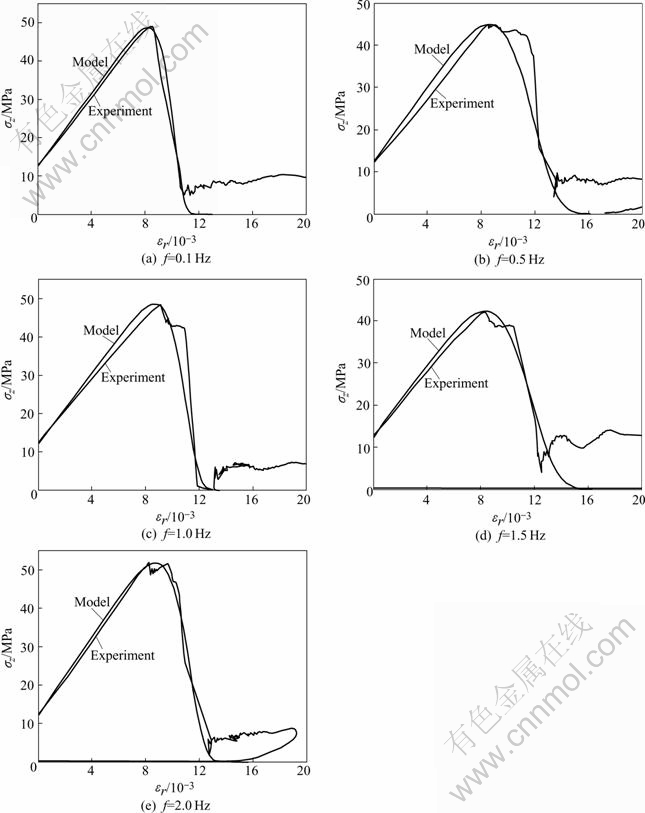
Fig.4 Experimental and theoretical 2D stress-strain curves of red sandstone experiencing different frequency of dynamic stress

Fig.5 Experimental and theoretical 2D stress—strain curves of red sandstone experiencing different vertical static stresses

4 Conclusions

By way of combining statistic damage model and viscoelastic model, 1D and 2D and 3D constitutive models of rock experiencing static-dynamic coupling loading are established. The verification experiment on 2D constitutive model under different static stresses and dynamic stresses with different frequencies are designed and performed. It is found that there is a good coherence between experimental stress—strain curves and theoretical stress—strain curves. Because of limitation of current technique, the systematic experimental verification for 3D constitutive models of rock waits to be performed, and it is significative to do such experiment.

References

[1] LI Xi-bing, GU De-sheng. Rock Impact Dynamics [M]. Shangsha: Central South University of Technology Press, 1994.(in Chinese)

[2] Grady D E,　Kioo M E. Dynamic Rock Fragmentation. in: Fracture Mechanics of Rock [M]. London: Academic Press, 1987. 429-475.

[3] Reinehart J S. Dynamic fracture strengths of rocks [A]. Proc Seventh Symp Mech [C]. Pensylvania State University, 1965.

[4] Zukas J A, Nicholas T, Swift H F, et al. Impact Dynamics [M]. New Youk: John Wiley & Sons,1982.

[5] Jaroslav B. Behaviour of rocks under high rates of strain [J]. Int J Acta Technica Csav, 1981, 18(5): 616-625.

[6] ZHANG Geng-de. The brittle fracture under dynamic load [J]. Chinese Journal of Geotechnical Engineering, 1981, 3(2): 43-49.(in Chinese)

[7] ZHANG Geng-de. Dynamic response of rock to impact load [J]. Explosion and Shock Waves, 1990, 10(3): 266-271.(in Chinese)

[8] LI Xi-bing, GU De-sheng. Energy dissipation of rock under impulsive loading [J]. Explosion and Shock Waves, 1994, 14(2): 129-139.(in Chinese)

[9] LI X B, et al. Stress and energy reflection from impact on rocks using different indenters [J]. Geotechnical and Geological Engineering, 2001, 19(2): 119-136.

[10] LI X B, et al. Oscillation elimination in the Hopkinson bar apparatus and resultant complete dynamic stress-strain curves for rocks [J]. Int J Rock Mech & Min Sci, 2000, 37(7): 1055-1068.

[11] Green J S, Perkins R D. Uniaxial Compression Tests at Varying Strain Rates on Three Geologic Materials, Basic and Applied Rock Mechanics [M]. Univ Texas, 1970.

[12] Olsson W A. The compressive strength of tuff as a function of strain rate from 10^-6 to 10³/sec [J]. Int J Rock Mech Min Sci & Geomech Abstr, 1991, 28(1): 115-118.

[13] Grady D E, Hollenbach R E, Schuler K W. Strain rate dependence in dolomite inferred from impact and static compression studies [J]. Int J Journal of Geophysical Research, 1982, 82(8): 1325-1333.

[14] CHEN Jing-xi. Similarities and differences of crack expanding under dynamic and static load [J]. Rock and Soil Mechanics, 1990, 11(2): 73-77.(in Chinese)

[15] Yale d p, Mobil R&D Corp, Jamieson w h Jr, Mobil E&P U.S. Inc. Static and dynamic rock mechanical properties in the Hugoton and panoma fields, Kansas [A]. Proceedings of the Mid-continent Gas Symposium [C]. Amarillo, TX, USA, 1994. 209-219.

[16] van HEERDEN W L. General relations between static and dynamic moduli of rocks [J]. Int J Rock Mech Min Sci & Geomech Abstr, 1987, 24(6): 381-385.

[17] Blanton T L. Effect of strain rates from 10^-2 to 10 sec^{-1 in triaxial compression tests on three rocks [J]. Int J Rock Mech Sci & Geomech Abstr, 1981, 18(1): 47-62.}

[18] WANG Wu-lin. Development on RDT-1000 high pressure dynamic triaxial instrument [J]. Rock and Soil Mechanics, 1989, 10(2): 69-82.(in Chinese)

[19] JU Qing-hai, WU Mian-ba. Experimental studies of dynamic characteristic of rocks under triaxial compression [J]. Chinese Journal of Geotechnical Engineering, 1993, 15(3): 73-80.(in Chinese)

[20] Logan J M, Handin J. Triaxial compression testing at intermediate strain rates [A]. George B C. Dynamic Rock Mechanics [M]. Port City Press, 1970. 167-194.

[21] Dyskin a v. On the role of stress fluctuations in brittle fracture [J]. Int J of Fracture, 1999, 100: 29-53.

[22] MA Chun-de. Experimental Study on Mechanics Properties of Rock Under Uniaxial Coupled Static-Dynamic Loading [D]. Changsha: Central South University, 2004.(in Chinese)

[23] ZUO Yu-jun, Li Xi-bing, ZHAO Guo-yan. A catastrophe model for dynamic fracture of static loaded rock [J]. Journal of China Coal Society, 2004, 29(6): 654-658.(in Chinese)

[24] ZUO Yu-jun, LI Xi-bing,　MA Chun-de, et al. Catastrophic model and testing study on failure of static loading rock system under dynamic loading [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(5): 741-746.(in Chinese)

[25] LI Xi-bing, ZUO Yu-jun, MA Chun-de. Constitutive model of rock subjected to static-dynamic coupling loading under intermediate strain rate [J]. Chinese Journal of Rock Mechanics and Engineering(adopted). (in Chinese)

[26] YU Ya-lun. Study on dynamic characteristic of rock with triaxial SHPB equipment [J]. Chinese Journal of Geotechnical Engineering, 1992, 14(3): 76-79.(in Chinese)

[27] LIU L Q, Katsabanis P D. Development of a continuum damage for blasting analysis [J]. Int J Rock Mech and Min Sci, 1997, 34(2): 217-231.

[28] QIN Yue-ping. Discussion on damage mechanics model and constitutive equation of rock [J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(4): 560-562. (in Chinese)

[29] SHANG Jia-lan, SHEN Le-tian, ZHAO Yu-hui, ZHAO Jian. Dynamic constitutive equation of the Bukit Timah granite [J]. Chinese Journal of Rock Mechanics and Engineering, 1998, 17(6): 634-641.(in Chinese)

[30] QIAO He, CAI Hua-you. Experimental study on dynamic constitutive equation of granite under explosive [J]. Chinese Journal of Rock Mechanics and Engineering, 1996, 15: 446-451.(in Chinese)

[31] LI Hai-bo, ZHAO Jian, LI Jun-ru, ZHOU Qing-chun, LIU Ya-qan. Study on constitutive relation of rock under dynamic compression based on energy balance during crack growth [J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(10): 1683-1688.(in Chinese)

[32] ZHEN Yong-lai, ZHOU Chen, XIA Song-you. Discussion on viscoelastic continuum damage constitutive model of rock and soil [J]. Journal of Hohai University, 1997, 25(2): 114-116.(in Chinese)

[33] SANO T O. Influence of strain rate on dilistion and strength of oshima granite under uniaxial compression[J]. Journal of Geophyscial Research, 1981, 86(B10): 9299-9311.

[34] Blanton T L. Effect of strain rates from 10^-2 to 10/s in triaxial compression tests on three rocks [J]. Int J Rock Mech and Min Sci, 1981, 18(1): 47-62.

[35] XIN Li-tian. The mechanical properties of rock under strong impact loading [J]. Chinese Journal of Geotechnical Engineering, 1996, 18(6): 61-68.(in Chinese)

[36] QI Cheng-zhi, QIAN Qi-hu. Physical mechanism of dependence of material strength on strain rate for rock-like material [J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(2): 177-181.(in Chinese)

[37] SHAN Ren-liang, XUE You-song, ZHANG Qian. Time dependent damage model of rock under dynamic loading [J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(11): 1771-1776.(in Chinese)

[38] LOU Wei-tao. A dynamic constitutive relation for calculating stress waves propagating in granite [J]. Explosion and Shock Waves, 1989, 9(3): 220-227.(in Chinese)

[39] LI Qing-bin, DENG Zong-cai, ZHANG Li-xiang. Dynamic damage constitutive model for concrete accounting for the difference of the initial elastic modulus [J]. J Tsginghua Univ (Sci & Tech), 2003, 43(8): 1088-1091.(in Chinese)

[40] Lindholm U S, Yeakley L M, Nagy A. The dynamic strength and fracture properties of dresser basalt [J]. Int J Rock Mech Min Sci & Geomech Abstr, 1974, 11(2): 181-191.

[41] ZHOU Guang-quan, LIU Xiao-ming. Viscoelascity Theory [M]. Hefei: Chinese Science Technology University Press, 1996.(in Chinese)

[42] JAEGER J C, COOK N G W. Fundamentals of Rock Mechanics [M]. London: Third Edition Chapman and Hall, 1979.

[43] CHEN Shi-hai, CUI Xin-zhuang. Dynamic damage constitution relation of rock with initial damage [J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21: 1955-1957.(in Chinese)

[44] ZHOU Xiao-ping, ZHANG Yong-xing, ZHU Ke-shan. Study on the complete stress-strain relation for mesoscopic heterogenous rock under treaxial compression with moderate or low lateral compressive stress [J]. Chinese Journal of Geotechnical Engineering, 2003, 25(5): 606-610.(in Chinese)

[45] LU Xiao-xia, ZHANG Pei-yuan. Rock damage viscoplastic constitutive relation with compressive [J]. Journal of Chongqing University(Natural Science Edition), 2002, 25(1): 6-9.(in Chinese)

[46] ZHOU Feng-hua, WANG Li-li, HU Shi-sheng. A damage-modified nonlinear visco-elastic constitutive relation and failure criterion of PMMA at high strain-rates [J]. Explosion and Shock Waves, 1992, 12(4): 333-342. (in Chinese)

[47] Grady D E, Kipp M E. Continuum modeling of explosive fracture in oil shale [J]. Int J Rock Mech Min Sci & Geomech Abstr, 1980, 17(2): 147-157.

[48] TANG Chun-an. Catastrophe in Rock Unstable Failure [M]. Beijing: The Coal Industry Press, 1993.(in Chinese)

[49] CHEN Dong-hui, LIN Zhong-ming, XIE He-ping, WANG Hong-wei. Damage study on brittle rock failure under complicated stress [J]. Journal of China Coal Society, 2004, 29(1): 31-35.(in Chinese)

[50] YANG Gui-tong, SHU Xue-feng. Plasticity Mechanics [M]. Beijing: Chinese Architectural Material Industry Press, 2000.(in Chiness)

[51] ZHAO J. Applicability of Mohr-Coulomb and Hoek-Brown strength criteria to the dynamic strength of brittle rock [J]. Int J Rock Mech & Min Sci, 2000, 37: 1115-1121.

Foundation item: Projects(10472134; 50490274; 50174056) supported by the National Natural Science Foundation of China; Project(2005038250) supported by China Postdoctoral Science Foundation

Corresponding author: LI Xi-bing; Tel: +86-731-8836628; E-mail: xbli@mail.csu.edu.cn

(Edited by PENG Chao-qun)