Trans. Nonferrous Met. Soc. China 29(2019) 123-131

Tribological properties and thermal-stress analysis of C/C-SiC composites during braking

Guan-yi CHEN¹, Zhuan LI¹, Peng XIAO¹, Xi OUYANG², Wen-jie MA³, Peng-tao LI², Jin-wei LI², Yang LI²

1. National Key Laboratory of Science and Technology for National Defence on High-strength Structure Materials, Central South University, Changsha 410083, China;

2. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China;

3. Institute of Science, Inner Mongolia First Machinery Group Co., Ltd., Baotou 014030, China

Received 28 December 2017; accepted 19 June 2018

Abstract: The tribological properties and thermal-stress behaviors of C/C-SiC composites during braking were investigated aiming to simulate braking tests of high-speed trains. The temperature and structural fields of C/C-SiC composites during braking were fully coupled and simulated with ANSYS software. The results of tribological tests indicated that the C/C-SiC composites showed excellent static friction coefficient (0.68) and dynamic friction coefficient (average value of 0.36). The highest temperature on friction surface was 445 °C. The simulated temperature field showed that the highest temperature which appeared on the friction surface during braking was about 463 °C. Analysis regarding thermal-stress field showed that the highest thermal-stress on friction surface was 11.5 MPa. The temperature and thermal-stress distributions on friction surface during braking showed the same tendency.

Key words: C/C-SiC composites; brake; tribological behavior; temperature field; thermal-stress field

1 Introduction

C/C-SiC composites, the carbon fibers reinforced carbon and silicon carbide dual matrices composites, are a new kind of high performance brake materials developed after carbon fibers reinforced carbon matrix (C/C) composites. C/C-SiC composites not only retain the advantages of C/C composites, but also overcome most of the disadvantages and possess some other excellent properties, such as higher thermal shock resistance, longer service life, especially lower sensibility to surroundings for a silicon carbide share of at least 20% in mass [1-3]. Due to their low coefficient of thermal expansion, high thermal conductivity and moderate modulus, C/C-SiC composites show excellent thermal shock stability. Among materials with low densities and high damage tolerance behavior, C/C-SiC composites show superior tribological properties indicating these materials to be one of the best candidates for advanced brake systems [4].

Up to now, the researches related to C/C-SiC composites are mainly concentrated on preparation methods, physical properties, tribological properties and their design of structure or properties. For instance, it was investigated by LI et al [5] that situ-grown carbon nanofibers can improve the tribological properties of C/C-SiC composites. LI et al [6] found that C/C-SiC composites showed excellent fatigue performance with high damage-tolerance. And KRENKEL and RERNDT [4] revealed that the C/C-SiC composites could be suitable materials for their applications in friction systems. However, the researches concerning the thermal field and thermal-stress fields of C/C-SiC composites during braking are rarely reported.

As for the applications in a brake system, the distributions of temperature and thermal-stress during braking are very significant because kinetic energy during braking is mainly absorbed as heat energy by braking systems and is dissipated into the surrounding atmosphere. Due to the generation of frictional heat on the interface of the disc and pad, there is rapid rise in temperature. When temperature of frictional surface exceeds the critical value of the given materials, it may lead to thermal cracks, excessive wearing or even braking failure [7-10].

With increasing the speed of high-speed trains, brake energy is correspondingly increasing. Huge heat load leads to cracks generation and propagation on the brake disc. So, it is important to determine the temperature and thermal-stress fields of the brake disc with precision when analyzing their failure mechanism and designing a new type of discs [10,11]. However, both the temperature and the thermal-stress during braking process are extremely difficult to measure. The temperature is usually measured by thermocouples at several measuring points of discs, but the analysis of thermal-stress magnitude would be quite difficult without analysis or design tools. Therefore, the system should be analyzed by simulation method in ANSYS software. In this way, the temperature and thermal-stress fields during braking could be simulated  precisely [12,13].

In this study, C/C-SiC brake composites were fabricated by chemical vapor infiltration (CVI) combined with liquid silicon infiltration (LSI). The tribological performance of C/C-SiC composites mated with self counterparts which simulated the braking conditions of high-speed trains was investigated. The temperature and thermal-stress fields of C/C-SiC composites under the same conditions were simulated and analyzed by finite element method (FEM) in ANSYS software.

2 Experimental

2.1 Preparation

The C/C-SiC composites were prepared by 2.5D needled carbon felt preform densified with CVI and  LSI. The preparation process including three major steps is described as follows [14]. The first step was the preparation of fabric preforms by the needling technique which started with repeatedly overlapping the layers of non-woven fiber cloth and short-cut fiber web with needle-punching step by step. The second step involved the production of C/C materials and densification in an isothermal furnace with CVI. The final step was a subsequent densification with LSI. After the preparation of materials, the ring samples were prepared for tribological tests. The detailed fabrication process of C/C-SiC samples was described in Ref. [2].

2.2 Test methods

The microstructures and morphologies of C/C-SiC composites were observed with scanning electron microscope (SEM, FEI Nova Nano SEM-230) equipped with energy dispersive X-ray spectroscope (EDX), three-dimensional digital video microscope (HIROXKH-7700) and optical microscope (OM, REUCHERT MeF3A).

The tribological properties were tested on an MM-3000 disc-on-disc type laboratory scale dynamo-meter. Both the stator and rotor were C/C-SiC composites. The parameters used in the tests are recapitulated in Table 1. Ten times pre-tests were conducted before formal tests to run in characteristic. A thermocouple was embedded within the stator to measure the temperature. It was located on the average friction radius and 1 mm beneath the friction surface. The formal test was repeated 20 times.

Table 1 Preselected parameters used in braking tests

The static friction coefficient was also tested on an MM-3000 dynamometer, which was after pre-tests and before formal tests. The dynamic friction coefficient was measured when the inertia disc was rotated slowly with the pressure loading on. The magnitudes of pressure and moment of inertia were the same as those of the formal tests.

3 Numerical modeling

3.1 Finite element method

It is a numerical technique for finding the approximate solutions to boundary value problems for partial differential equations. It uses subdivision of a whole problem domain into simpler part, called finite element and solves the problem by minimizing an associated error function. The subdivision of the whole domain has several advantages [15]: accurate represent-tation of the complex geometry; inclusion of dissimilar of the solution; easy representation of the solution; capture of the local effects and so on.

It divides the domain into a group of sub-domains; every sub-domain is represented by a set of element equations of the original domain.

To simplify the analysis, several assumptions have also been made as follows [12].

(1) All kinetic energy is converted into frictional heat or heat flux.

(2) The heat transfer for this analysis only involves heat conduction and convection. The heat radiation can be neglected in this analysis because of small amount (about 5%). The heat transfer efficiency is about 90%.

(3) In this study, the ambient temperature and initial temperature are set to be 20 °C.

(4) The C/C-SiC composites are considered to be orthotropic in this study, because the properties parallel and perpendicular to the fiber cloth are different.

According to heat transfer theory, the transient heat conduction equation of the material with an axisymmetric structure and without inner heat source in the cylindrical coordinates is [16]

        (1)

with the boundary and initial conditions shown as follows:

(1) q_n=h(T-T_∞) on Γ₁

(2) q_n=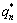 on Γ₂

(3) T=25 °C when t=0

where ρ, c, k_r and k_z are the density, specific heat  capacity, thermal conductivities in r and z directions of the material, respectively. Also, h is the heat convection coefficient, 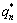 is the heat flux at each contact interface due to friction, T_∞ is the ambient temperature, T₀ is the initial temperature, and Γ₁ and Γ₂ are the boundaries on which temperature, convection and heat flux are imposed, respectively.

3.2 Modeling and meshing

The 3D model of C/C-SiC composite sample was established in SOLIDWORKS software (as shown in Fig. 1(a)). The elements used for meshing of the sample are 3D elements with 10 nodes (Fig. 1(b)).

Fig. 1 3D model of C/C-SiC composites sample in SOLIDWORKS software (a) and meshing of C/C-SiC composites sample in ANSYS software (b)

3.3 Heat flux

The heat flux entering the sample surface was calculated by the following formula [17]:

q(r, t)=ημp(r, t)v(r, t)=ημp(r, t)ω(t)r              (2)

where q is heat flux entering the friction surface; η is the distribution rate of the heat flux on each surface (in this study, the brake test was conducted under self-ring condition, so the value of η is 0.5); μ is friction coefficient; p(=P/S) is the pressure per unit area; ν is the linear velocity; and ω is the angular velocity.

To simplify the analysis, it is assumed that the density contribution of C/C-SiC composites is homo- geneous during braking; the braking pressure is distributed uniformly on the surface. Thus, the heat flux is related to time and radius.

3.4 Determination of convection coefficient

The thermal analysis of the braking system requires a precise determination of the quantity of heat flux as well as the distribution of this energy between the rotor and stator. During braking, some of the frictional heat unavoidably escapes in the air ambient by convection. Consequently, the determination of the convection coefficient is essential. Their exact calculation is rather difficult, because these coefficients depend on the structure of the braking system, the speed of the vehicle and consequently of the air circulation [18].

In this study, the heat convection coefficient (h)  on each surface was calculated by the following  method [19]:

The h depends on the state of the air movement, the physical properties of air, the shape of the sample and the temperature gradient between the sample surface and ambient. The computational formula is:

h=Nuλ/l₀                                    (3)

where λ is the heat conductivity of the air (W/(m·K)); l₀ is the size of solid surface (m), Nu is Nusselt number and it can be determined by following items.

(1) The outside surfaces of sample

During braking, the heat convection between outside surface and air belongs to forced convection heat transfer, so for the vortex of a bare cylinder, Nu can be calculated by the empirical formula:

     (4)

where Re is the rotating Reynolds number and Pr is the Prandtl number.

At the end of braking, the heat convection between outside surface and air belongs to free convection heat transfer in infinite space, so Nu can be calculated by the empirical formula:

(5)

where Gr is the Grashof number.

(2) Internal surfaces of sample

For the whole braking process, the heat convection between internal surface and air belongs to free convection heat transfer in confined space, so Nu can be calculated by the empirical formula:

          (6)

where Gr_δ is the Grashof number in the area with feacture size of δ.

4 Results and discussion

4.1 Microstructure

After the sample preparation, the morphologies of C/C-SiC composites were observed by SEM (as shown in Fig. 2). With the help of the energy dispersive spectrometer (EDS), it was known that the black regions in the Fig. 2(a) were carbon fiber reinforced pyrolytic carbon (PyC) matrix, known as C/C material, and the gray or white regions were SiC matrix or residual Si. Figure 3 showed the morphologies of the cross section and surface of C/C-SiC composites. The layered structure can be seen obviously in Fig. 3(a), and SiC was formed among the fiber bundles in the non-woven web, inside the short-cut fabric and around the needing fibers. During LSI process, the molten silicon can only infiltrate into the macroscopic pores of the inter-bundle zone because of capillarity and react with carbon matrix to form SiC. Although there are pores in the fiber bundles, silicon can only infiltrate part of them and the other pores are so small that the formed SiC prevents the molten Si from further diffusion.

Fig. 2 SEM image of C/C-SiC composites (a) and distributions of silicon (b) and carbon (c) analyzed by EDS

Fig. 3 Microstructures of C/C-SiC composites

4.2 Tribological properties

The results of tribological tests were presented in Figs. 4 and 5. The brake curve (Fig. 4) showed that the braking process lasted for about 10 s, and the whole process could be divided into three stages. In the early stage, the friction coefficient was high; in the middle stage, the friction coefficient decreased and became steady; in the later stage, the friction coefficient increased and approached to maximum value at the end of braking process. The results of tribological tests indicated that the C/C-SiC composites showed excellent character with high static friction coefficient (0.68) and average dynamic friction coefficient (0.36).

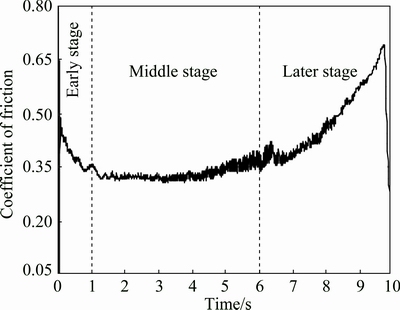
Fig. 4 Typical braking curve of C/C-SiC composites

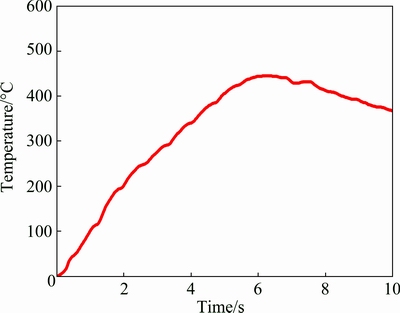
Fig. 5 Experimental temperature curve of C/C-SiC composites during braking

The temperature variation on friction surface measured by thermocouple during braking was shown in Fig. 5. The highest temperature of the surface was 445 °C at t= 6.2 s.

Fig. 6 3D morphologies of friction surface before (a) and after (b) tribological tests

Fig. 7 Morphologies of friction surface before (a) and after (b) tribological tests

Braking is a mutual interaction process between two relative motional worn surfaces, so the tribological characteristics are usually determined by microstructure and worn surface. The optical micrographs of the friction surface of C/C-SiC composites were shown in Figs. 6 and 7. It can be seen that there were asperities on the friction surface (shown in Fig. 6(a)) before tribological tests. After tests, continuous friction films appeared on the friction surface (shown in Fig. 7(b)). These films played a lubricated role during braking. And it was noticed that cracks were generated, propagated, and converged during the braking process compared with the surface before tests shown in Fig. 7(a).

In the early stage, the asperities on the friction surface made the surface very rough, so the friction coefficient was high. Then, under the action of pressure, shear stress and high rotational speed, the asperities fractured and some of asperities were extruded and deformed into friction films which lubricated the contact surface. The continuous films formed in the middle stage which led to low and steady friction coefficient. In the later stage, the rotational speed and shear stress decreased sharply. As a result, some of friction films fell off while new films were increasingly difficult to be formed, leading to an increased friction coefficient at the end of braking process.

4.3 Temperature field simulation results

Temperature determines the thermo-mechanical behavior of the structure. During braking, temperature and thermal gradient levels are very high. This generates stress and deformation manifested by the appearance and the accentuation of cracks. It is then important to precisely determine the temperature field of the brake disc. During braking, temperature is not stabilized on the disc, so a transient analysis is required [11,20].

In this work, brake conditions in simulation were listed in Table 2, and some general properties of C/C-SiC composites were listed in Table 3 [21,22].

Table 2 Brake conditions in simulation

Table 3 General properties of brake sample of C/C-SiC composites

Figure 8 showed the variation of the maximum temperature versus time during raking for the C/C-SiC composites. It was noticed that the temperature increased rapidly until T_max= 463.4 °C at t=4.7 s. Then, it began to decrease over time. Indeed, huge heat generated on friction surface during braking leads to the increase of the surface temperature. As the rotational speed decreases, the heat flux also declines. This heat on one aspect will be conducted into bodies because of heat conduction, and on the other aspect will be dissipated in air due to heat convection. The processes of heat transfer will be intensified as the thermal gradient around surfaces increases. When the heat generation on the friction surface is less than the heat loss, temperature will decrease. Compared with the experimental temperature curve of C/C-SiC composites, it can be observed that the temperatures in simulation are pretty close to the experimental ones, which proves the validity of the finite element method.

Fig. 8 Maximum temperature variation of whole sample during braking

However, there were still some deviations between the simulation and experiment for the temperature on friction surface. As a whole, the simulation temperature was higher than the experimental temperature, because in experiment, heat radiation was also a way of thermal dissipation beside the heat convection. The wear debris ejected from the friction surface was also a form of thermal dissipation. These were ignored in the simulation, thus the experimental temperature increased more slowly compared with the simulation results.

Figure 9 showed the instantaneous temperature distribution of the whole body (Fig. 9(a)) and friction surface (Fig. 9(b)) at the moment when the temperature reached the maximum value. It was shown that the maximum temperature (463.4 °C at t=4.7 s) appeared on the friction surface due to the heat generation. The temperature gradient in the axial direction was greater than that in the radial direction because the conductivity parallel to the carbon fiber was larger than that perpendicular to carbon fiber. Temperature on the friction surface was variable with radius and increased firstly from the center to surrounding and then decreased. It was because the heat flux grew with radius and there was huge heat convection when the radius got to the maximum.

Fig. 9 Temperature distributions of C/C-SiC composites for whole body (a) and friction surface (b) during braking

4.4 Thermal-stress field simulation results

During braking, the dissipation of the frictional heat generated is important. Temperature changes of the brake cause axial and radial deformation, and then in turn, the change in shape affects the contact between the rotating ring and stationary ring. In this study, the structural and thermal results were coupled to analyze the thermal-stress field.

Figure 10 showed the variation of maximum thermal-stress versus time for the whole body and friction surface during braking. It was shown that there were three peaks on the thermal-stress curve for the whole body, and the first peak occurred when the thermal-stress on friction surface got to the maximum (about 11.5 MPa at t=0.45 s). In the early braking stage, the heat flux at the beginning was high and the heat conduction firstly happened on the friction surface. This led to the great thermal gradient on friction surface, which caused high thermal-stress. The second peak was when the thermal-stress approached to 11.8 MPa at t=1.56 s. Another peak appeared at t=2.28 s and the thermal-stress got to 11.9 MPa.

Fig. 10 Maximum thermal-stress variation of whole sample and friction surface during braking

Figure 11 presented the distributions of the thermal-stress for the whole body and friction surface when the thermal-stress reached the first peak value in Fig. 10. It was also proved that the first peak appeared on the friction surface (as shown in Fig. 11(a)). For the friction surface, the thermal-stress distribution (Fig. 11(b)) showed the same tendency as that of the temperature distribution.

Fig. 11 Thermal-stress distributions of whole sample (a) and friction surface (b) during braking at t=0.45 s

According to the braking curve (Fig. 4) and thermal-stress curve (Fig. 10), it is predicted that cracks on the friction surface are generated and propagate mainly in the early braking stage. Because in this stage, rotational speed and friction coefficient are high and unstable, which cause high level shear stress and mechanical vibration besides the high thermal-stress. Then, in the middle stage, the thermal-stress decreases sharply and the friction coefficient is low and steady. Finally, in the later stage, the thermal-stress is very low and the rotational speed approaches to zero even though the friction coefficient increases to the maximum value.

5 Conclusions

(1) The average dynamic friction coefficient C/C- SiC composites during braking was 0.36. And the temperature curve showed that the highest temperature on the friction surface was 445 °C.

(2) The friction films formed during braking, which led to decreasing of friction coefficient in the middle braking stage. And the cracks propagated and converged on the friction surface during braking, thus life and performance of the brake were affected.

(3) The simulated temperature field on the friction surface showed that the highest temperature was 463.4 °C, which agreed well with the experimental result. The axial thermal gradient was greater than radial gradient because the axial thermal conductivity was less than the radial thermal conductivity. The maximum thermal-stress value on the friction surface was 11.5 MPa. The thermal-stress distributions on the friction surface were symmetric with the temperature distributions.

(4) It was predicted that, the cracks were generated and propagated mainly in the early stage of the braking process because of the high rotational speed, high and unstable friction coefficient and high thermal-stress in this period.

References

[1] KRENKEL W, HENKE T. Design of high performance CMC brake disks [J]. Key Engineering Materials, 1998, 164: 421-424.

[2] XIAO Peng, LI Zhuan, XIONG Xiang. Microstructure and tribological properties of 3D needle-pinched C/C-SiC brake composites [J]. Solid State Sciences, 2010, 12(4): 617-623.

[3] LI Zhuan, XIAO Peng, XIONG Xiang, ZHU Su-hua. Tribological characteristics of C/C-SiC braking composites under dry and wet conditions [J]. Transactions of Nonferrous Metals Society of China, 2008, 18(5): 1071-1075.

[4] KRENKEL W, BERNDT F. C/C-SiC composites for space applications and advanced friction systems [J]. Materials Science and Engineering A, 2005, 412(1-2): 177-181.

[5] LI Zhuan, XIAO Peng, ZHANG Ben-gu, LI Yang, LU Yu-hai. Preparation and tribological properties of C/C-SiC brake composites modified by in situ grown carbon nanofibers [J]. Ceramics International, 2015, 41(9): 11733-11740.

[6] LI Yang, XIAO Peng, LUO Heng, ALMEIDA R S M, LI Zhuan, ZHOU Wei, BRüCKNER A, REICHERT F, LANGHOF N, KRENKEL W. Fatigue behavior and residual strength evolution of 2.5D C/C-SiC composites [J]. Journal of the European Ceramic Society, 2016, 36(16): 3977-3985.

[7] JIANG Lan, JIANG Yan-li, YU Liang, SU Nan, DING You-dong. Thermal analysis for brake disks of SiC/6061 Al alloy co-continuous composite for CRH3 during emergency braking considering airflow cooling [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(11): 2783-2791.

[8] HUSSAIN H, KHANDWAWALA A I. Application of transient thermal analysis for three feeder design optimization for sand casting [J]. International Journal of Mechanical Engineering and Technology, 2013, 4(6): 241-248.

[9] DUFRENOY P, WEICHERT D. A thermomechanical model for the analysis of disc brake fracture mechanisms [J]. Journal of Thermal- stresses, 2003, 26(8): 815-528.

[10] COLIN F, FLOQUET A, PLAY D. Thermal contact simulation in 2-D and 3-D mechanisms [J]. ASME Journal of Tribology, 1988, 110(2): 247-252.

[11] BELHOCINE A, BOUCHETARA M. Thermal analysis of a solid brake disc [J]. Applied Thermal Engineering, 2012, 32(1): 59-67.

[12] BELHOCINE A, BOUCHETARA M. Structural and thermal analysis of automotive disc brake rotor [J]. Archive of Mechanical Engineering, 2014, 61(1): 89-113.

[13] XIA Ming. Thermo-mechanical coupled particle model for rock [J]. Transactions of Nonferrous Metals Society of China, 2015, 25(7): 2367-2379.

[14] LI Zhuan, XIAO Peng, ZHANG Ben-gu, LI Yang, LU Yu-hai, ZHU Su-hua. Preparation and dynamometer tests of 3D needle-punched C/C-SiC brake composites for high-speed and heavy-duty brake systems [J]. International Journal of Applied Ceramic Technology, 2016, 13(3): 423-433.

[15] JAISWAL R, JHA A R, KARKI A, DAS D, JAISWAL P, RAJHADIA S, BASNET A. Structural and thermal analysis of disc brake using Solidworks and ANSYS [J]. International Journal of Mechanical Engineering and Technology, 2016, 7(1): 67-77.

[16] CHOI J H, LEE I. Finite element analysis of transient thermoelastic behavior in disk brakes [J]. Wear, 2004, 257(1-2): 47-58.

[17] LEI Bao-ling, YI Mao-zhong, XU Hui-juan. Simulation of temperature field of carbon/carbon composite during braking [J]. The Chinese Journal of Nonferrous Metals, 2008, 18(3): 377-382. (in Chinese)

[18] ZHANG Jian, XIA Chang-gao. Research of the transient temperature field and friction properties on disc brakes [J]. Advanced Materials Research, 2013, 756-759: 4331-4335.

[19] WANG Bu-xuan. Engineering heat and mass transfer [M]. Beijing: Science Press, 1998: 139-226. (in Chinese)

[20] KIM D J, LEE Y M, PARK J S, SEOK C S. thermal-stress analysis for a disk brake of railway vehicles with consideration of the pressure distribution on a friction surface [J]. Materials Science and Engineering A, 2008, 483(1): 456-459.

[21] FAN Shang-wu, ZHANG Li-tong, XU Yong-dong, CHENG Lai-fei, LOU Jian-jun, ZHANG Jun-zhan, YU Lin. Microstructure and properties of 3D needle-punched carbide brake materials [J]. Composites Science & Technology, 2007, 67(11-12): 2390-2398.

[22] KRENKEL W. Handbook of ceramic composites [M]. Heidelberg: Springer, 2004: 117-148.

C/C-SiC复合材料在制动过程中的摩擦磨损性能及热应力仿真分析

陈冠一¹，李 专¹，肖 鹏¹，欧阳曦²，马文杰³，李鹏涛²，李金伟²，李 杨²

1. 中南大学 轻质高强结构材料国防科技重点实验室，长沙 410083；

2. 中南大学 粉末冶金国家重点实验室，长沙 410083；

3. 内蒙古第一机械制造(集团)有限公司 科研所，包头 014030

摘  要：为了研究C/C-SiC复合材料的摩擦磨损性能及制动过程中的热应力行为，对C/C-SiC复合材料进行模拟高铁制动条件下的自对偶摩擦磨损测试，同时在ANSYS有限元模拟软件中对制动过程的温度及结构场进行耦合。结果显示，C/C-SiC复合材料在制动过程中表现出优异的静摩擦因数(0.68)以及动摩擦因数(平均值为0.36)；摩擦面的最高温度为445 °C。模拟的温度场结果显示，摩擦面的最高温度为463 °C。模拟热应力场结果显示，制动过程中摩擦面上的最大热应力为11.5 MPa。摩擦面上的温度与热应力分布呈相似趋势。

关键词：C/C-SiC复合材料；制动；摩擦磨损行为；温度场；热应力场

(Edited by Wei-ping CHEN)

Foundation item: Project (51575536) supported by the National Natural Science Foundation of China; Project (2016YFB0301403) supported by the National Key Research and Development Program of China; Project (2017zzts435) supported by Graduate Degree Thesis Innovation Foundation of Central South University, China

Corresponding author: Zhuan LI; Tel: +86-13574842740; E-mail: lizhuan@csu.edu.cn

DOI: 10.1016/S1003-6326(18)64921-0