J. Cent. South Univ. (2018) 25: 1976-1986

DOI: https://doi.org/10.1007/s11771-018-3888-3

Conventional triaxial compression on hollow cylinders of sandstone with various fillings: Relationship of surrounding rock with support

WU Qiu-hong(吴秋红)^{1, 2, 3}, LI Xi-bing(李夕兵)¹, TAO Ming(陶明)¹,ZHAO Fu-jun(赵伏军)⁴, WENG Lei(翁磊)⁵, DONG Long-jun(董陇军)¹

1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;

2. Work Safety Key Laboratory on Prevention and Control of Gas and Roof Disasters for Southern Coal Mines, Hunan University of Science and Technology, Xiangtan 411201, China;

3. Hunan Provincial Key Laboratory of Safe Mining Techniques of Coal Mines, Hunan University of Science and Technology, Xiangtan 411201, China;

4. School of Resources, Environment and Safety Engineering, Hunan University of Science and Technology, Xiangtan 411201, China;

5. School of Civil Engineering, Wuhan University, Wuhan 430072, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: The interaction of surrounding rock with a support system in deep underground tunnels has attracted extensive interest from researchers. However, the effect of high axial stress on tunnel stability has not been fully considered. In this study, compression tests with and without confining pressure were conducted on solid specimens and hollow cylinder specimens filled with aluminium, lead, and polymethyl methacrylate (PMMA) to investigate the strength, deformation and failure characteristics of circular roadways subjected to high axial stress. The influence of the three-dimensional stress on the surrounding rock supported with different stiffness was studied. The results indicate that the strength and peak strain of hollow cylinders filled with PMMA are higher than those of hollow cylinders filled with aluminium or lead, indicating that flexible retaining is beneficial for roadway stability. The results obtained in this paper can contribute to better understanding the support failure of a buried roadway subjected to high axial stress and thus to analyzing and evaluating roadway stability.

Key words: mechanical properties; hollow cylinder; flexible retaining; axial stress; support stiffness

Cite this article as: WU Qiu-hong, LI Xi-bing, TAO Ming, ZHAO Fu-jun, WENG Lei, DONG Long-jun. Conventional triaxial compression on hollow cylinders of sandstone with various fillings: Relationship of surrounding rock with support [J]. Journal of Central South University, 2018, 25(8): 1976–1986. DOI: https://doi.org/10.1007/ s11771-018-3888-3.

1 Introduction

As underground mining goes deeper, roadways are subjected to complicated mining-induced stresses, producing many unconventional rock failures [1–4], such as zonal disintegration phenomenon, rock ejection and spalling. One serious problem is that conventional supporting systems become invalid frequently [5–7]. Therefore, there is an urgent need to study the interaction between the surrounding rock and the support system to provide a safe underground mining space.

Extensive research has studied roadway support in recent years. So far, the support strategy tends to make full use of the rock's self-support capacity. For example, NATM considers the surrounding rocks as part of the entire support system. The support types developed are multi-support or combined support systems, such as anchor cables, bolt-mesh-anchors and pre-stressed anchor ropes [8, 9]. The supporting material changes from being a wooden support to an energy absorption support, highly resistant to high stress and large deformations [10–12]. The loading condition for the support system used in the experiment can meet the requirements of a wider range of loading rates, by using developed dynamic testing equipment [13, 14], including the drop hammer impact machine, SHPB.

Numerical simulations and field investigations are conducted to study the support in underground engineering [15, 16]. In addition, physical model experiments in the laboratory are also available and direct methods, making it easier to understand the mechanism of rock instability [17–19]. WANG [20] conducted similar simulation experiments on a roadway in soft rock, to study the effect of support strength on the deformation of the surrounding rock. MENG et al [21] analyzed the causes of repeated failures and repairs of Xinshanghai No. 1 coal mine ingate and obtained the appropriate support resistance through physical model testing.

The gravitational stress of the rock mass increases gradually with the increasing of mining depth. For example, the gravitational stresses of the roadways in a coal mine at a burial depth of 1200 m, the water-conveyance tunnels at a burial depth of 2500 m and the roadways in a metal mine at a burial depth of 3900 m reach 30, 60, 100 MPa, respectively, and the horizontal stresses along the axial direction may be greater. Due to complex geological conditions underground, it is common to find that the strike layout of roadway is parallel to the direction of the in situ stress [22, 23]. A significant factor influencing the stability of surrounding rock is abnormally high geo-stress along the roadway’s axis [24–27]. However, previous analyses on the stress state of the surrounding rock are mostly based on the assumption of the plane strain problem [28–30]. Alternatively, the axial stress is assumed to be the intermediate principal stress along the roadway axis, ignoring the sensitivity of the high axial stress on the roadway. With an increased knowledge of deep rock mechanics, it has been found that the stability of the surrounding rock is closely related to axial stress [31–33]. JIA et al [33] found that the circular failure pattern of zonal disintegration is more likely to be formed when the horizontal stress in the direction of the tunnel axis is the maximum principal stress. However, few studies presented consider the effect of the supporting rock on the stability of the roadway subjected to high axial stress. The roadway is in a three-dimensional stress state when it is subjected to high axial stress. The stress analysis and supporting design for the roadway, with plane strain considerations, is not conducive for controlling the stability of the surrounding rock.

To study the effect of the supports on the stability of the circular roadway subjected to high axial stress, this work tests hollow cylinders with aluminium, lead and polymethyl methacrylate (PMMA) using uniaxial and conventional triaxial tests. This provides a new way to interpret the interaction between the roadway, its supports and their surrounding rock, taking into consideration the three-dimensional stress effect of the surrounding rock.

2 Laboratory model

The main function of roadway support is to provide a radial force to help the surrounding rock to achieve a state of stress equilibrium and stability of deformation. The radial force is commonly described as support intensity, and the real supporting conditions of a roadway are shown in Figure 1(a).

The solid rock specimen in the laboratory test serves as the rock mass, and the hollow cylinder specimen serves as the simplified underground openings. The use of hollow cylinders in experiments for studies dates back to the early 20th century [34, 35]. Many researchers have used hollow cylinder specimens to study the deformation and fracture characteristics of underground openings [36–41]. SANTARELLI et al [42] examined the possibility of predicting the behaviour of rocks around model underground excavations from the results of hollow cylinder compression tests. LABIOUSE et al [43] investigated the effect of excavation on nuclear waste disposal, by using hollow cylinders of clay, and confirmed the need to appropriately consider the mechanical anisotropy of clay bedding.

However, these hollow cylinder test studies mainly focused on the hole’s effect on the rock’s mechanical properties. Their results did not show the relationship between the deformation and strength characteristics of the surrounding rock and supporting materials. To provide a new way to interpret the interaction among the roadway, supports and their surrounding rock, this work tests very specific samples by uniaxial and conventional triaxial tests. These tests simulate the real-life interaction among the roadway, support and its surrounding rock in an underground mine.

The purpose-built test sample consists of two parts: one is a hollow cylinder sandstone rock with 100 mm in length, 16 mm in hole diameter and 50 mm in external diameter; the other is a solid column with a diameter of 15 mm, filled in the hollow part of the hollow cylinder rock. Three types of solid columns are used here, aluminium, lead, and polymethyl methacrylate (PMMA), which simulate the different support strengths in the roadway. The interface between the solid column and rock specimen was bonded using marble glue, and the elastic modulus of the binder was 2–5 GPa. The end of the solid column was processed to be approximately 2.5 mm shorter than the rock specimens. When the coupled hollow cylinders were prepared, the uniaxial and triaxial compression tests are conducted, as shown in Figure 1(b). As the filling is not subjected to axial stress during the testing process, a radial force between the rock and filling will, inevitably, be generated when the loading lasts for a certain amount of time, resisting the lateral deformation of the inner wall, and preventing failure of the rock. Clearly, the mechanism of the filling is the same as that of the real support system, which provides a radial force to make the stress state of the inner wall recover to a 3D state, as shown in Figure 1(c).

Previous studies use the inner hole pressure to simulate the support intensity [20]. In this work, we use different filling materials to study the effect support intensity on the surrounding rock and the parameters of the fillings, which are presented in Table 1.

3 Experimental methods and preparation

3.1 Specimen preparation

The sandstone for the experiments was obtained from Changlong, Sichuan Province, and consisted of quartz and feldspar with no visible defects. First, solid specimens with a diameter of 50 mm and a height of 100 mm were drilled, of which some specimens were processed into hollow cylinders with an inner diameter of 16 mm. Then, the hollow cylinders were filled with different materials, including aluminium, lead and PMMA, as shown in Figure 2.

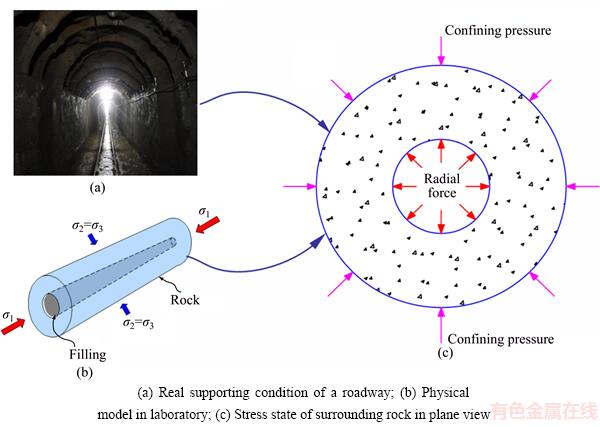
Figure 1 Relation between surrounding rock and support:

Table 1 Mechanical parameters of fillings

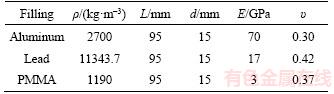
Figure 2 Photo of some specimens

All specimens were divided into five groups, labelled SS, HC, FA, FL and FP to represent the solid specimen, hollow cylinder and hollow cylinder filled with aluminium, lead, and polymethyl methacrylate (PMMA), respectively. The density of each specimen ranged from 2185.3 kg/m³ to 2405.7 kg/m³; the P-wave velocity ranged from 2152.9 m/s to 2648.4 m/s, indicating that the specimens were homogeneous. The specimens were polished at their ends to limit unevenness to less than 0.05 mm, and stayed naturally dry indoors for 7 d.

3.2 Testing methods

The electro-hydraulic servo control system SAW-2000 was employed to conduct the experiments. The rock specimens were loaded by displacement control, with loading rates of 0.01 mm/s for uniaxial compression, and 0.005 mm/s for conventional triaxial compression. Confining pressures levels were set to 5, 20, 30 and 45 MPa with a loading rate of 0.5 MPa/s via pressure control.

4 Experimental results

4.1 Uniaxial compression experiments

The parameters of the specimens from these experiments are listed in Table 2. The elastic modulus equals the slope of the straight line phase of the stress–strain curve. The typical stress–strain curves obtained from the uniaxial compression experiments are plotted in Figure 3, showing that the specimens experienced four stages of compaction, elasticity, yielding and failure. The deformation in the compaction stage for the solid specimen was much larger, indicating that a large number of microcracks exist within the specimen. The drop in stress in the pre-peak stage shown in the curve is attributed to the final outcome of the microcrack propagation in the rock. The rock shows clear brittle behaviour, presenting a quick stress drop at the post-peak stage.

Table 2 Mechanical parameters of specimens under uniaxial compression

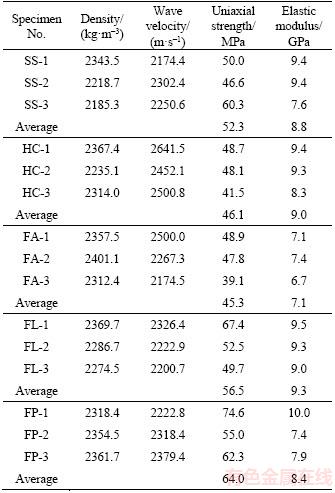
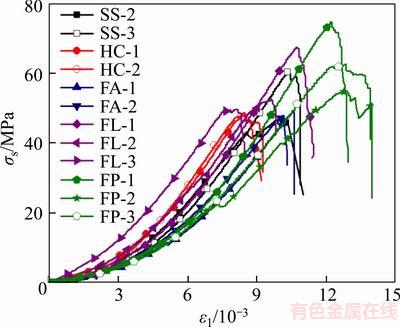
Figure 3 Uniaxial compression stress–strain curves of sandstone specimens

The strength of the hollow cylinder (46.1 MPa) is 12% lower than that of the solid specimen(52.3 MPa). This is because the inner free surface of the hollow cylinder contributes to local deformation, reducing the overall strength of the specimen. However, the elastic modulus of the solid specimen (8.8 GPa) has no obvious discrepancy from that of the hollow specimen(9.0 GPa), indicating that there is almost no effect of the hole on the elastic modulus of the hollow cylinder.

The strength of group FA is lower than that of the other four groups. Since the elastic modulus of aluminium is eight times that of sandstone, the lateral deformation of the hole wall is fully restricted by the aluminium bar. The strength in group FL (56.5 MPa) is 24.7% greater than that of group FA (45.3 MPa) because the lead is soft and ductile, and the elastic modulus of lead is 1.93 times that of sandstone. This permits lateral deformation to some extent and restricts rocks falling from the inner wall. The strength of group FP (64.0 MPa) is 13.3% greater than that of group FL (56.5 MPa). PMMA is a transparent high-molecular compound with only 0.18 times the elastic modulus of lead. Under the same axial loading, PMMA has a lower radial stress, permitting the rock to have larger compatible deformations than groups FA and FL, as seen in Figure 3.

4.2 Triaxial compression experiments

The differences in the principal stress–strain curves for the five groups of specimens under triaxial compression are plotted in Figure 4. The experimental results obtained from the triaxial compressions are presented in Table 3. Strength increases as confining pressure increases in the solid specimen, as shown in Figure 4. The curve shows an obvious compaction stage when the confining pressure is 5 MPa. When the confining pressure reaches 20 MPa, the initial phase of the principal stress–strain curve clearly shows linear deformation. The peak strength appears as a yield plateau, meaning that the plastic deformation of the specimen continues to increase. However, the bearing capacity remains constant, and it mainly relies on the crack friction in the yielding deformation process. The bearing capacity and plastic deformation of the sample increases as the confining pressure increases.

Compared to the solid specimen, when the confining pressure is 5 MPa, the stress–strain curve of the hollow specimen shows a clear stress-drop phenomenon, showing obvious brittle characteristics, as seen in Figure 4. There is no yield plateau in the curve for the hollow specimen, which is the main difference between the solid specimen and the hollow specimen because the inner hole induces a non-uniform stress distribution around the hole wall. The minimum principal stress in the hole wall is lower, so the hollow specimen does not enter the ductile stage. The inner wall first loses bearing capacity with increasing deformation, and the failure area gradually increases.

The stress–strain curves of the three types of filled specimens are similar to that of the hollow cylinder specimen, which also shows a clear stress-drop phenomenon under lower confining pressure. The strengths of group FA, group FL and group FP increase with increasing confining pressure. The peak strain of group FP is much larger than that of the other groups, as seen in Figure 4. The peak strain for group FP is approximately twice that of group FA at a confining pressure of 5 MPa.

As shown in Figure 4, when the confining pressure reaches 45 MPa, the curves of the five groups present yield plateaus, while no drop in stress occurs. The specimens experience strain softening phases and residual deformation stages. The residual strength of group FP (261 MPa) is the highest compared with other groups. The residual strengths of group SS (199 MPa), group FA(192 MPa) and group FL (207 MPa) are all greater than that of group HC (118 MPa). Although the rock has macroscopic fracture planes when the filled specimen reaches its peak strength, rock fragments are tightly stuck to the filling materials, and the filled specimen does not experience macroscopic shear sliding. This result indicates that the bearing capacity of the filled specimens is a combination of both friction between the rock and the filling material and the internal fissure friction of rock, enhancing the residual strengths of the filled specimens.

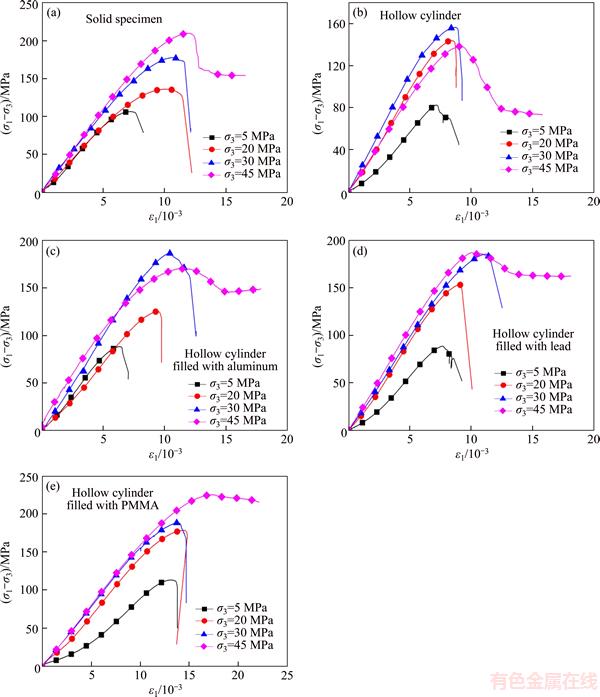
Figure 4 Triaxial compression stress–strain curves of five groups specimens

5 Mechanical properties of specimens

5.1 Strength and deformation of specimens

The relationship between strength and confining pressure is plotted in Figure 5(a). Under the confining pressure of 5 MPa, the strengths of the specimens in group SS and group FP show no obvious discrepancy; both are larger than those of the other three groups. The triaxial strengths, for the five groups of specimens under 5 MPa confining pressure, are much greater than the uniaxial compression strengths. This result occurs because a large number of microcracks exist inside the rock [44–47], resulting in lower uniaxial strength. In addition, the failure type is different under different stress conditions [3]. The rock is often split along the axis under uniaxial compression, while the rock often fails in shear under triaxial compression.

The strength of the solid specimens increases with increasing confining pressure. The strengths of the hollow cylinders increase slowly and are less than that of the other types of specimens when the confining pressure is 30 MPa and 40 MPa, as seen in Figure 5(a). For group FP, the strengths under different confining pressures are greater than those of the other four groups, and increase with increasing confining pressure. However, the strengths of the group FA and FL also increase slowly under higher confining pressure; the strengths of specimens FA-7 and FL-7 are 25.8% and 16.4%, respectively, which are both lower than that of specimen FP-7.

Table 3 Mechanical parameters of specimens under triaxial compression

The elastic modulus of the specimens under the confining pressure is higher than that under uniaxial compression, indicating the confining pressure significantly influences the elastic modulus because the confining pressure is beneficial for closing microcracks, as seen in Figure 5(b). The elastic modulus of solid specimens increases with increasing confining pressure. The elastic modulus values of group HC and group FA change greatly with confining pressure. However, there is no obvious change in the elastic modulus for groups FL and FP under different confining pressures. The elastic modulus of group FP is the lowest, while that of group FL is the highest, with the difference approximately 28.7% under the confining pressure of 45 MPa.

The peak strain of the hollow cylinder specimen is remarkably, lower than that in the other four groups, with the peak strain of group FP being highest, as seen in Figure 5(c). Under a confining pressure of 45 MPa, the peak strain of group FP is 47.4% higher than that of group FA and is 72.3% higher than that of group FL.

Figure 5 Comparison among five types of sandstones:

When the confining pressure is loaded, the stress distribution around the hole wall is non-uniform. The total axial strain of the outer and inner wall is the same, but the locations adjacent to the hole wall fail first due to minor principal stress, so the strength and peak strain of the hollow cylinder are less than those of the other groups. The filling material will support the rock after filling the hole with materials, making the stress state of the hole wall recover to a 3D state. The stiffness of the filling greatly influences the strength and deformation of the specimen. The greater the stiffness of the filling material is, the greater the induced radial force will be and the easier the rock slips to failure, so the strength and peak strain of the specimen are relatively low and the elastic modulus of the specimen is relatively high. Likewise, the smaller the stiffness of the filling material is, the smaller the induced radial force will be, and the larger the deformation under the same axial loading is; thus, the strength and peak strain of group FP are the highest, and the elastic modulus of group FP is the lowest.

5.2 Failure pattern of specimens

For uniaxial compression, the solid specimen and hollow cylinder specimen fail mainly in shear with local tensile failure. While mixed shear and tensile failures are often observed for the filled specimens; the rock is not split apart, as it is stuck to the filled material.

The failure types of some specimens under triaxial compression are shown in Figure 6. For the solid specimens, only one main fracture face is found under triaxial compression, as seen in Figure 6(a). The onion-skin fracture is induced around the hole wall under the confining pressures of 30 MPa and 45 MPa, as shown in Figures 6(b) and (c). When the confining pressure reaches 45 MPa, a large amount of spalling is seen, indicating that failure starts from the inside towards the outside for the hollow specimens. This result is similar to the results of previous work conducted in conventional triaxial compression testing [36, 37].

Under triaxial compression, the inner stress distribution is non-uniform for the hollow specimen. The maximum principal stress of the hole wall is in the tangential direction to the axial direction with axial loading, while the minimum principal stress is always the radial stress. As deformation increases, failure in the hollow specimen starts from the hole wall for the minor principal stress, and the rest of the specimen continues to bear the loading until the whole rock specimen is in the yield state. However, the hollow cylinder specimen fails in shear. The hollow cylinder specimen failing under axial compression indicates that high axial stress has a significant effect on the occurrence of onion-skin fractures around the inner hole.

Figure 6 Failure modes of specimens in triaxial compression:

Figures 6(d), (e) and (f) present the failure types of group FA, group FL and group FP. The failure pattern is simple for the filled specimens under confining pressure. Only one shear fracture face is formed, and the rock fragments are tightly stuck to the filling materials because the bearing capacity of the rock is reinforced by the materials in the hole. In addition, the contact faces of the rock and the filling material are held together by the adhesive and shear resistance forces.

6 Conclusions

1) The existence of the filling material changes the rock stress state, making the rock in the inner wall recover to a 3D stress state. The filling material resists the lateral deformation of the inner wall, preventing the rock falling from the free surface.

2) The filling has a significant influence on the mechanical properties of the specimens in the plastic deformation phase. A smaller stiffness of the filling leads to weaker radial action on the rock specimen, which makes the specimen bear more axial loading and larger deformation.

3) The failure of rock does not indicate the disappearance of its bearing capacity. For the filled samples, the bearing capacity is a combination of both the friction between the filling material and the rock and the internal fissure friction of rock.

4) The strength and the peak strain of the hollow cylinders filled with PMMA are higher than those of the hollow cylinders filled with aluminium or lead. The rock fragments stay adhered rather than separating from the specimens. Therefore, flexible retaining is beneficial for roadway stability.

References

[1] ORTLEPP W D, STACEY T R. Rock burst mechanisms in tunnels and shafts [J]. Tunnelling and Underground Space Technology, 1994, 9: 59–65.

[2] MARTIN C D, READ R S, MARTINO J B. Observation of brittle failure around a circular test tunnel [J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(7): 1065–1073.

[3] DIEDERICHS M S, KAISER P K, EBERHARDT E. Damage initiation and propagation in hard rock during tunneling and the influence of near-face stress rotation [J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41: 785–812.

[4] WENG L, HUANG L Q, TAHERI A, LI X B. Rock burst characteristics and numerical simulation based on a strain energy density index: A case study of a roadway in Linglong gold mine, China [J]. Tunnelling and Underground Space Technology, 2017, 69: 223–232.

[5] JIAO Y Y, SONG L, WANG X Z, ADOKO A C. Improvement of the U-shaped steel sets for supporting the roadways in loose thick coal seam [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 60(2): 19–25.

[6] LI C C. Field observations of rock bolts in high stress rock masses [J]. Rock Mechanics and Rock Engineering, 2009, 43(4): 491–496.

[7] KANG H, WU Y, GAO F, LIN J, JIANG P. Fracture characteristics in rock bolts in underground coal mine roadways [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 62(5): 105–112.

[8] SCHUMACHER, F P, KIM E. Modeling the pipe umbrella roof support system in a Western US underground coal mine [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 60(6): 114–124.

[9] LI Shu-cai, WANG Hong-tao, WANG Qi, JIANG Bei, WANG Fu-qi, GUO Nian-bo, LIU Wen-jiang, REN Yao-xi. Failure mechanism of bolting support and high-strength bolt-grouting technology for deep and soft surrounding rock with high stress [J]. Journal of Central South University, 2016, 23(2): 440–448.

[10] CHARETTE F, PLOUFFE M. Roofex: Results of laboratory testing of a new concept of yieldable tendon [C]// POTVIN Y. Deep Mining 07, Proceeding of the 4th International Seminar on Deep and High Stress Mining. Perth: Australian Centre for Geomechanics, 2007: 395–404.

[11] VARDEN R, LACHENICHT R, PLAYER J, THOMPSON A, VILLAESCUSA E. Development and implementation of the Garford dynamic bolt at the Kanowna belle mine [C]// 10th Underground Operators’ Conference. Launceston, Australia, 2008: 95–102.

[12] LI C C. A new energy-absorbing bolt for rock support in high stress rock masses [J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(3): 396–404.

[13] HADJIGEORGIOU J, POTVIN Y. A critical assessment of dynamic rock reinforcement and support testing facilities [J]. Rock Mechanics and Rock Engineering, 2011, 44(5): 565–578.

[14] LI C C, DOUCET C. Performance of d-bolts under dynamic loading [J]. Rock Mechanics and Rock Engineering, 2012, 45(2): 193–204.

[15] SHEN B. Coal mine roadway stability in soft rock: A case study [J]. Rock Mechanics and Rock Engineering, 2013, 47(6): 2225–2238.

[16] FENG X T, HAO X J, JIANG Q, LI S J, HUDSON J A. Rock cracking indices for improved tunnel support design: A case study for columnar jointed rock masses [J]. Rock Mechanics and Rock Engineering, 2016, 49(6): 2115–2130.

[17] GRASSELLI G. 3D behaviour of bolted rock joints: experimental and numerical study [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(1): 13–24.

[18] JALALIFAR H, AZIZ N, HADI M. The effect of surface profile, rock strength and pretension load on bending behaviour of fully grouted bolts [J]. Geotechnical and Geological Engineering, 2006, 24(5): 1203–1227.

[19] FU H Y, JIANG Z M, LI H Y. Physical modeling of compressive behaviors of anchored rock masses [J]. International Journal of Geomechanics, 2011, 11(3): 186–194.

[20] WANG C. The optimal support intensity for coal mine roadway tunnels in soft rocks [J]. International Journal of Rock Mechanics & Mining Sciences, 2000, 37(7): 1155–1160.

[21] MENG B, JING H, CHEN K, SU H. Failure mechanism and stability control of a large section of very soft roadway surrounding rock shear slip [J]. International Journal of Mining Science and Technology, 2013, 23(1): 127–134.

[22] GALE W J, BLACKWOOD R L. Stress distributions and rock failure around coal mine roadways [J]. International Journal of Rock Mechanics and Mining Science and Geomechanics Abstracts, 1987, 24(3): 165–173.

[23] ZHU Z, LI Y, XIE J, LIU B. The effect of principal stress orientation on tunnel stability [J]. Tunnelling and Underground Space Technology, 2015, 49: 279–286.

[24] BROWN E T, HOEK E. Trends in relationships between measured in-situ, stresses and depth [J]. International Journal of Rock Mechanics and Mining Science and Geomechanics Abstracts, 1978, 15(4): 211–215.

[25] KANG H P, ZHANG X, SI L P, WU Y Z, GAO F Q. In-situ stress measurements and stress distribution characteristics in underground coal mines in China [J]. Engineering Geology, 2010, 116(3, 4): 333–345.

[26] WANG S, WU Z, GUO M, GE X. Theoretical solutions of a circular tunnel with the influence of axial in situ stress in elastic–brittle–plastic rock [J]. Tunnelling and Underground Space Technology, 2012, 30: 155–168.

[27] JIA P, YANG T H, YU Q L. Mechanism of parallel fractures around deep underground excavations [J]. Theoretical and Applied Fracture Mechanics, 2012, 61(1): 57–65.

[28] BROWN E T, BRAY J W, LADANYI B, HOEK E. Ground response curves for rock tunnels [J]. Journal of Geotechnical Engineering, 1983, 109(1): 15–39.

[29] CARRANZA-TORRES C, FAIRHURST C. The elasto- plastic response of underground excavations in rock masses that satisfy the Hoek–Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36: 777–809.

[30] MARTIN C D, KAISER P K, MCCREATH D R. Hoek- Brown parameters for predicting the depth of brittle failure arou [J]. Canadian Geotechnical Journal, 1999, 36(1): 136–151.

[31] LU A Z, XU G S, SUN F, SUN W Q. Elasto-plastic analysis of a circular tunnel including the effect of the axial in situ stress [J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(1): 50–59.

[32] QIAN Q, ZHOU X, XIA E. Effects of the axial in situ stresses on the zonal disintegration phenomenon in the surrounding rock masses around a deep circular tunnel [J]. Journal of Mining Science, 2012, 48(2): 276–285.

[33] JIA P, ZHU W C. Mechanism of zonal disintegration around deep underground excavations under triaxial stress—Insight from numerical test [J]. Tunnelling and Underground Space Technology, 2015, 48(11): 1–10.

[34] ADAMS F D. An experimental contribution to the question of the depth of the zone of flow in the earth's crust [J]. Journal of Geology, 1912, 20(2): 97–118.

[35] KING L V. On the limiting strength of rocks under conditions of stress existing in the earth’s interior [J]. Journal of Geology, 1912, 20(2): 119–138.

[36] GAY N C. Fracture growth around openings in thick-walled cylinders of rock subjected to hydrostatic compression [J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1973, 10(3): 209–233.

[37] EWY R T, COOK N G W. Deformation and fracture around cylindrical openings in rock II: Initiation, growth and interaction of fractures [J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1990, 27(5): 409–427.

[38] FRANCOIS B, LABIOUSE V, DIZIER A, MARINELLI F, CHARLIER R, COLLIN F. Hollow cylinder tests on boom clay: Modelling of strain localization in the anisotropic excavation damaged zone [J]. Rock Mechanics and Rock Engineering, 2014, 47(1): 1–16.

[39] LABIOUSE V, VIETOR T. Laboratory and in situ simulation tests of the excavation damaged zone around galleries in opalinus clay [J]. Rock Mechanics and Rock Engineering, 2014, 47(1): 57–70.

[40] WU Qing-liang, LU Ai-zhong, GAO Yong-tao, WU Shun-chuan, ZHANG Ning. Stress analytical solution for plane problem of a double-layered thick-walled cylinder subjected to a type of non-uniform distributed pressure [J]. Journal of Central South University, 2014, 21(5): 2074–2082.

[41] WU Qiu-hong, LI Xi-bing, ZHAO Fu-jun, TAO Ming, DONG Long-jun, CHEN Lu. Failure characteristics of hollow cylindrical specimens of limestone under hole pressure unloading [J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(6): 1424–1433. (in Chinese)

[42] SANTARELLI F J, BROWN E T. Failure of three sedimentary rocks in triaxial and hollow cylinder compression tests [J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1989, 26(89): 401–413.

[43] LABIOUSE V, SAUTHIER C, YOU S. Hollow cylinder simulation experiments of galleries in boom clay formation [J]. Rock Mechanics and Rock Engineering, 2014, 47(1): 43–55.

[44] ZHAO Y L, ZHANG L Y, WANG W J, WAN W. Transient pulse test and morphological analysis of single rock fractures [J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 91: 139–154.

[45] ZHAO Y L, ZHANG L Y, WANG W J, TANG J Z. Cracking and stress–strain behavior of rock-like material containing two flaws under uniaxial compression [J]. Rock Mechanics and Rock Engineering, 2016, 49(7): 2665–2687.

[46] ZHAO Y L, ZHANG L Y, WANG W J, WAN W, LI S Q, MA W H, WANG Y X. Creep behavior of intact and cracked limestone under multi-level loading and unloading cycles [J]. Rock Mechanics and Rock Engineering, 2017, 50(6): 1–16.

[47] ZHAO Y L, WANG Y X, WANG W J, WAN W, TANG J Z. Modeling of non-linear rheological behavior of hard rock using triaxial rheological experiment [J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 93: 66–75.

(Edited by YANG Hua)

中文导读

含不同充填物厚壁圆筒砂岩试样的常规三轴压缩试验：围岩与支护关系的研究

摘要：深部地下硐室围岩与支护的相互作用关系研究已经吸引了研究者的广泛兴趣。然而，较高轴向应力对硐室稳定性的影响并没有得到充分考虑。基于单轴和常规三轴压缩试验，采用完整试样、空心、铝棒、铅棒及有机玻璃充填的厚壁圆筒试样，模拟研究三维应力状态下不同刚度支护对圆形巷道的强度、变形和破坏特征的影响。结果表明，充填低刚度有机玻璃的试样，其强度最高，峰值变形最大，因而柔性支护有利于维持巷道的稳定。研究结果为理解具有较高轴向应力深埋巷道支护的失效行为，分析和评估巷道的稳定性提供了参考。

关键词：力学特性；厚壁圆筒；柔性支护；轴向应力；支护刚度

Foundation item: Projects(11772357, 51474103, 51504092) supported by the National Natural Science Foundation of China; Project(2016YFC0600706) supported by the National Key Research and Development Program of China

Received date: 2017-03-27; Accepted date: 2017-09-24

Corresponding author: TAO Ming, PhD; Tel: +86–15367941151; E-mail: mingtao@csu.edu.cn