DOI: 10.11817/j.issn.1672-7207.2015.04.014
基于混沌的DCSK调制方法及性能分析
黄乘顺1,王少杰1,宗鹏2
(1. 邵阳学院 信息工程系,湖南 邵阳,422000;
2. 南京航空航天大学 航天学院,江苏 南京,210016)
摘要:针对混沌调制实用化过程中存在的问题,提出产生混沌序列的新颖算法及优选准则。介绍CSK和COOK调制模型及DCSK调制解调模型,对DCSK,CSK和BPSK调制模型的性能进行仿真分析与对比。分析CSK和DCSK信号中半个比特周期(T/2)内所产生的混沌样值个数L对CSK和DCSK性能的影响,并介绍一种新颖的DCSK改进型调制方式。研究结果表明:与CSK相比,DCSK调制对信道畸变不敏感并具有更好的噪声特性,在误码率RBE为10-3数量级时可提高信道噪声约3 dB;在信噪比(Eb/No)不小于12 dB的条件下,DCSK的RBE与CSK的相比小1个数量级以上。
关键词:混沌;差分混沌键控;混沌同步;混沌调制;误码率
中图分类号:TN91 文献标志码:A 文章编号:1672-7207(2015)04-1268-06
DCSK modulation and performance analysis based on chaos
HUANG Chengshun1, WANG Shaojie1, ZONG Peng2
(1. Department of Information Engineering, Shaoyang University, Shaoyang 422000, China;
2. College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
Abstract: To solve the problems existing in practical application on chaotic modulation, a new arithmetic and criteria for generating and optimizing chaotic sequences were proposed. The modulation models of chaos shift keying (CSK), chaotic on-off keying (COOK) and the modulation-demodulation models of differential chaos shift keying (DCSK) were illustrated. The numerical simulations and results comparison of CSK, DCSK and binary phase shift keying (BPSK) modulations were detailed. The effects of L chaotic samples generated in half the bit duration on CSK and DCSK performance were presented. A novel improved DCSK modulation was also introduced, The results show that the DCSK modulation is not sensitive to abnormal change of channel and has better noise performance than the CSK. DCSK can improve noise performance about 3 dB when bit error rate (RBE) is level of 10-3. When signal to noise ratio (Eb/No) is greater than 12 dB, the bit error rate of DCSK is at least one order of magnitude less than that of CSK.
Key words: chaos; differential chaos shift keying (DCSK); chaotic synchronization; chaotic modulation; bit error rate
随着非线性和混沌理论的逐步成熟,混沌理论具有广阔的应用领域,如:在电力系统管理方面,可用合作协同进化及神经网络法对电力市场出清电价进行预测[1-2],也可应用相空间重构和最大Lyapunov指数的计算进行市场出清电价预测[3]。但由于混沌系统具有类随机性特点,混沌技术尤其适合于通信系统。一般认为混沌通信系统具有以下优势[4-5]:1) 混沌信号的宽频特性可以实现某种意义上的扩频;2) 混沌信号的似噪声、难预测的特性特别适合于保密通信;3) 因为混沌序列数量众多、类随机而且确定可再生,故特别适合于多址通信。混沌调制解调是实现混沌通信的关键,因此,对混沌调制技术的研究具有重要意义。实际上,混沌通信技术还处于实用化过程中的初始阶段,在实际应用中还有诸多问题有待解决。如在信道噪声干扰下如何降低误码率RBE及调制系统中混沌同步方法的研究,都是目前国内外研究混沌通信的热点问题。本文作者从混沌序列的优选问题入手,研究对比新的混沌调制模型,研究混沌调制解调系统的模型及提高系统性能,并简化系统的硬件结构,提高计算速度。
1 混沌序列的产生及优选
1.1 混沌序列的产生
混沌调制解调器的硬件结构及性能与混沌序列的产生方法及混沌序列的性能有直接关系。图1所示为DCSK混沌调制系统框图,其中混沌发生器产生调制所需的混沌序列。混沌序列的产生方法有多种,其中:一种方法是用模拟电路产生混沌信号[6],其特点是实时性较好,但系统的复杂度较高,且对器件的要求较高,在实际应用中,元器件较难满足要求;另一种方法是用数字电路产生,如基于典型Logistic映射的实现方法[7]的特点是电路形式简单,系统复杂度低。还可采用迭代算法,用MATLAB软件产生混沌序列[8],该方法实现简单,系统复杂度低,对器件无太高要求,其缺点是算法的运算量大。本文以Logistic-Map映射为例,介绍一种改进的迭代算法即整数实现算法。Logistic-Map 混沌映射的定义为
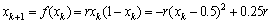 ;
;
1≤r≤4;0<xk<1

图1 DCSK调制系统框图
Fig. 1 Diagram of DCSK modulation
式中:k=0,1,2,…。可见,Logistic-Map 映射值xk是区间(0,1)内的小数。若选r=4,则有
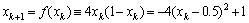 (1)
(1)
将(0,1)范围内的小数xk写成
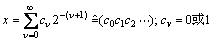 (2)
(2)
取前M位表示成x,忽略后面的位(其中的量化误差是不可避免的),则
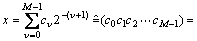
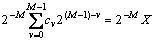 (3)
(3)
其中: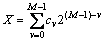 。可见:X是1个整数(由二进制数表示),并且整数X与小数x一一对应。由式(1),(2)和(3)可得r=4时的Logistic-Map 映射的整数表达式为
。可见:X是1个整数(由二进制数表示),并且整数X与小数x一一对应。由式(1),(2)和(3)可得r=4时的Logistic-Map 映射的整数表达式为
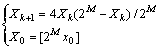 (4)
(4)
据此可用数字硬件方法产生混沌序列。而在通常情况下,式(1)中的混沌序列发生器中的迭代运算一般采用双精度浮点数计算, 但双精度浮点计算过于费时,且不便于数字硬件实现。式(4)的整数实现算法可提高计算速度,简化硬件电路,因此,优于浮点运算。
1.2 混沌序列的优选准则
混沌发生器产生的混沌序列由于具有类随机性特点,其性能在通常情况下比传统的线性扩频序列性能稍差,因此,还需要对所产生的序列进行优选。优选后的序列可改进混沌调制解调系统的性能,如系统的计算速度、计算精度、系统硬件结构、抗多用户干扰及系统的同步性等[9]。
优选准则包括平衡性准则、自相关准则和互相关准则。优选的方法是将混沌发生器产生的混沌序列依次进行平衡性、自相关性和互相关性检测。只有当序列的平衡性、自相关性、互相关性都不超过所设定的阀值时,该序列才作为优选序列,其余序列则被弃用。
另外,在相干调制解调器中,混沌序列的预测及混沌同步是混沌通信系统中必须解决的实际问题。混沌系统的同步方法有很多,如主动控制同步法[10]、基于观测器的同步法[11-12]、自适应控制法[13]、Backstepping法[14]、耦合同步法等。最近研究的最多方法就是耦合同步法[15],可用耦合映射格子(CMLs)模型实现混沌同步。在实际的混沌调制解调器设计时,为避免混沌同步的实现困难,主要采用非相干调制解调方法,如CSK,COOK和DCSK等。
2 混沌调制解调模型
2.1 CSK与COOK调制的数学模型
混沌调制方式包括混沌掩盖(chaotic masking)、混沌键控(chaos shift keying,CSK)、混沌开关键控(chaotic on-off keying,COOK)、差分混沌键控(differential chaos shift keying,DCSK)及以上调制方式的改进形式。
CSK是一种数字调制方式。设m为调制信号源(m1,m2,…,mN为码元信息),已调信号为y(k),xi(k)(i=1,2,…,N) 是具有不同特性的N个混沌信号发生器产生的信号(其对应的连续信号表示为y(t),x(t),下同)。下面考虑一种特殊情况下的CSK调制,即离散系统只有2个混沌发生器:
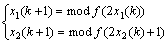 (5)
(5)
其中: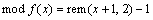 ;
;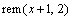 表示
表示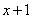 对2求余数,并且在区间[0, 2)之间取值。复序列产生器对应的函数用
对2求余数,并且在区间[0, 2)之间取值。复序列产生器对应的函数用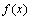 表示,则离散时间基带调制信号以调相形式发送,即
表示,则离散时间基带调制信号以调相形式发送,即
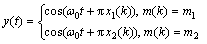 (6)
(6)
将已调信号映射到复平面的单位圆上,则已调信号可写成
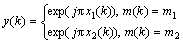 (7)
(7)
由此可得到初始值在单位圆上的复平面内的混沌序列发生器:
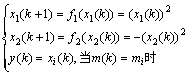 (8)
(8)
混沌开关键控(COOK)是CSK的一种特殊情况,它只采用1个混沌信号发生器,根据待发送的二进制数字信息源进行开关切换,以决定已调输出信号。COOK调制的数学模型如下:
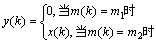
2.2 DCSK调制解调
在DCSK系统中,所传送的二进制信号的每个信息码元mi用2个不同的混沌抽样函数代替。其中一个抽样函数作为参考信号,第2个抽样函数作为信息的载波。对于码“1”,参考信号将在2个T/2 时间内被连续传送2次;对于码“0”,前T/2时间传送参考信号,后T/2时间传送其反向的参考信号。DCSK调制系统框图如图1所示,DCSK调制的数学模型可用以下传输函数表示:
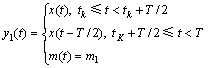

其中:T为周期;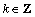 。因为每个信息码元在其2个T/2时间内分别被映射为2个相关的混沌函数相继传送,所以,可以通过相关器和过零比较器判决解调原信号。图2所示为DCSK混沌解调系统的框图,接收端相关器的输出(即积分器的输出)为zi。
。因为每个信息码元在其2个T/2时间内分别被映射为2个相关的混沌函数相继传送,所以,可以通过相关器和过零比较器判决解调原信号。图2所示为DCSK混沌解调系统的框图,接收端相关器的输出(即积分器的输出)为zi。

图2 DCSK解调系统框图
Fig. 2 Diagram of DCSK demodulation
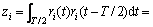
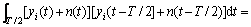
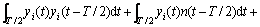
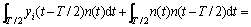
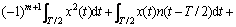
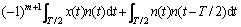 (9)
(9)
其中: 为半个抽样函数周期内的积分。分析式(9)可知出现了交叉项
为半个抽样函数周期内的积分。分析式(9)可知出现了交叉项 和
和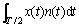 。定义1个随机变量为
。定义1个随机变量为
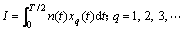 (10)
(10)
其中:xq(t)为载有有限能量的混沌基函数,并且经过信道滤波时没有发生任何畸变;n(t)为经过射频带宽为2B的理想带通滤波器,双边功率谱为N0/2的高斯白噪声过程。假定式(10)为时变积分变换,对于给定的q,该变换是时不变的。由于零均值平稳高斯过程经过线性时不变变换后仍然是零均值平稳高斯过程,其二阶距与方差相同。
定义Dq为式(10)中固定值q的随机变量,则Dq的方差为
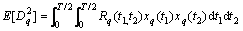
其中: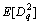 为
为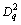 的均值;Rq(t1,t2)为信道噪声的自相关函数,由此{Dq}的统计特性可通过计算得到;{I}的统计特性可从并行线性时不变积分变换得到。对Dq的随机特性分析可得第q个积分变换的方差为
的均值;Rq(t1,t2)为信道噪声的自相关函数,由此{Dq}的统计特性可通过计算得到;{I}的统计特性可从并行线性时不变积分变换得到。对Dq的随机特性分析可得第q个积分变换的方差为
 (11)
(11)
其中:[ ]表示均值。从式(11)可见:方差与q无关,即每个并行积分变换的输出都将服从零均值和式(11)中方差的高斯分布。因此,前述交叉项的统计特性与混沌基函数无关。
经分析发现:与CSK和COOK调制方式相比,DCSK是一种反极性调制方式,除了能获得较好的噪声性能以外,其优点在于噪声判决门限值为0 dB,与信噪比无关;另外,DCSK的一个更重要优点在于:由于参考混沌信号和载信息的混沌信号通过同样的信道,使得该调制方式对信道畸变不敏感,若在每个码元间隔内信道参数保持为常数,则DCSK可适用于任何时变信道。
2.3 DCSK调制的改进
新型调制模型的研究是混沌通信的主要内容之一。若将DCSK调制与混沌相位调制相结合,则可进一步提高信息的传输速率,其调制性能接近FSK调制性能[16]。
若同时采用DCSK(差分混沌键控)与CDSK(相关延迟键控)调制技术,则可构成另一种新颖调制方式,即CD-DCSK调制(相关延迟-差分混沌键控调制)。设y(t)为调制器的输出信号,x(t)为混沌信号,τ为时间延迟,高低位数字信号a和b均分别代表传输“+1+1,-1+1,+1-1,-1-1”4种情况,则CD-DCSK调制器的输出信号为
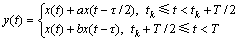
与DCSK解调器中的符号一样,CD-DCSK的解调器中的r(t)是解调器的输入信号,通过相关器的积分相关域值运算,发送的信息Za和Zb分别为
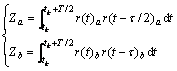 (12)
(12)
考虑到接收信号r(t)中含有信道噪声ζ(t),由于噪声信号的相关特性,式(12)可写成:

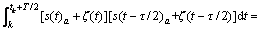
 (13)
(13)
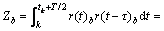
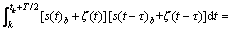
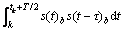 (14)
(14)
将接收端的阀值门限判决设为0,则当Za>0和 Zb>0时,能解调出传输信息a或b为+1;当Za<0和Zb<0时,能解调出a或b为-1(当然也可以选择判决为反相传输信号),从而实现信号的解调。CD-DCSK调制的误码率RBE为[17]
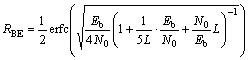 (15)
(15)
其中:Eb为数字信息每个bit 的能量;N0为噪声功率;Eb/N0为信噪比;L为已调信号中半个周期(T/2)内所产生的混沌样值的个数;erfc为误差函数。
3 混沌调制的性能分析与仿真
根据Frobenius-Perron operator(FPO)理论,对混沌信号的统计特性进行分析,可分别得到CSK调制、DCSK调制的误码率(RBE)计算公式,并与BPSK调制下的误码率RBE 计算公式进行对比。
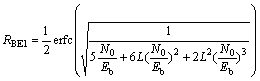 (16)
(16)
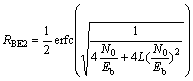 (17)
(17)
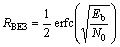 (18)
(18)
式中:RBE1,RBE2和RBE3分别为CSK,DCSK和BPSK调制时的误码率。在白高斯信道(AWGN)条件下,对CSK调制、DCSK调制的RBE 进行仿真(L分别设定为10,20和80),并与BPSK调制进行比较,仿真结果如图3~5所示。
从图3~5可以看出:与传统的BPSK调制相比,混沌调制(CSK调制及DCSK调制)的RBE比传统BPSK的大,这是混沌序列的类随机特性所致;当RBE相同时,CSK的Eb/N0比BPSK的Eb/N0增大8~10 dB,但DCSK的Eb/N0比BPSK的Eb/N0只增大6 dB 左右,可见DCSK对信道噪声与失真不敏感,在RBE为10-3数量级时可增大信道噪声约3 dB;当Eb/N0较小(即信道噪声较大)时,DCSK的RBE 也比CSK的小;当Eb/N0较大时,DCSK的RBE 明显比CSK的小,尤其是当Eb/N0不小于12 dB时,DCSK的RBE 比CSK的1个数量级以上;当L增大时,虽然DCSK相对于CSK的RBE更小,但与L较小时相比,CSK和DCSK的RBE都会相应变小,而BPSK的RBE不变,这符合式(16),(17)和(18)的计算结果。因此,在混沌调制器的设计中,已调信号中每个周期内的混沌样值的个数L不宜选择过大,应选取合适的L。同时,对上述DCSK的改进型调制方式(即CD-DCSK调制)进一步分析可发现:CD-DCSK在较好的传输信道条件下具有更好的传输性能,而且具有更高的保密性和传输速率。
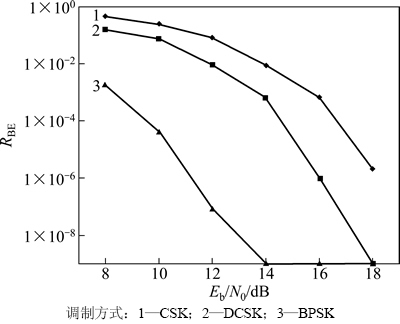
图3 L=10时的误码率RBE比较
Fig. 3 Comparison of RBE when L=10
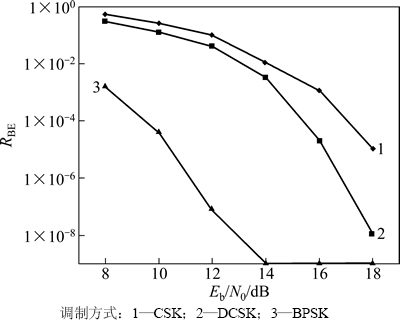
图4 L=20时误码率RBE比较
Fig. 4 Comparison of RBE when L=20
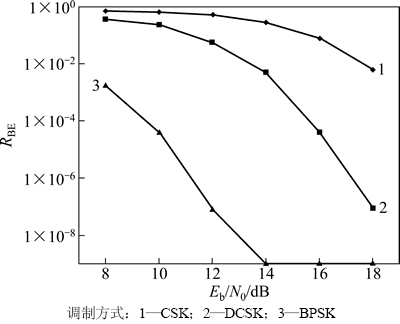
图5 L=80时的误码率RBE比较
Fig. 5 Comparison of RBE when L=80
4 结论
1) 介绍了混沌调制解调技术实用化过程中存在的实际问题及解决方法。提出采用整数实现算法产生混沌序列,它优于双精度浮点运算法;此外,还提出了混沌序列的优选准则及方法。
2) 与CSK调制比较,DCSK调制对信道畸变不敏感,具有良好的噪声性能,可改进信道噪声约3 dB,适用于在时变信道中传输;从仿真结果看,DCSK的误码率RBE 明显比CSK的小,尤其是在良好的信道环境下(如Eb/N0不小于12 dB),DCSK的RBE 比CSK 的小1个数量级以上。
3) 介绍了一种DCSK调制的改进型,并给出了该模型的数学推导、解调端的数据判决方法及误码率计算公式,有利于对混沌调制模型进行进一步研究。
参考文献:
[1] Karsaz A, Mashhadi A R, Mirsalehi M M. Market clearing price and load forecasting using cooperative co-evolutionary approach[J]. International Journal of Electrical Power & Energy Systems, 2010, 32(5): 408-415.
[2] Singhal D, Swarup K S. Electricity price forecasting using artificial neural networks[J]. International Journal of Electrical Power & Energy Systems, 2011, 33(3): 550-555.
[3] 杨淑霞, 徐琳茜, 刘达, 等. 基于最大Lyapunov指数的市场出清电价预测[J]. 中南大学学报(自然科学版), 2011, 42(12): 3791-3796.
YANG Shuxia, XU Linqian, LIU Da, et al. Market clear price forecasting based on maximum Lyapunov exponent[J]. Journal of Central South University (Science and Technology), 2011, 42(12): 3791-3796.
[4] 黄乘顺, 李星亮. 基于混沌的扩频通信系统及性能分析[J]. 通信技术, 2008, 41(12): 37-39.
HUANG Chengshun, LI Xiangliang. Spread-spectrum communication system and its performance analysis based on chaos[J]. Communications Technology, 2008, 41(12): 37-39.
[5] 赵耿, 方锦清. 现代信息安全与混沌保密通信应用研究的进展[J]. 物理学进展, 2003, 23(2): 210-255.
ZHAO Geng, FANG Jinqing. Modern information safety and advances in application research on chaos-based security communication[J]. Progress in Physics, 2003, 23(2): 210-255.
[6] Ghobad H B, Clare D McGillen. A chaotic direct-sequence spread spectrum communication system[J]. IEEE Transaction on Communications, 1994, 42(2/3/4): 1524-1527.
[7] 王亥, 胡健栋. Logistic-Ma混沌扩频序列[J]. 电子学报, 1997, 25(1): 19-23.
WANG Hai, HU Jiandong. Logistic-map chaotic spread-spectrum sequence[J]. Acta Electronica Sinica, 1997, 25(1): 19-23.
[8] 王军选, 刘联会. 混沌理论及其在通信中的应用[J]. 现代电子技术, 2002(6): 60-62.
WANG Junxuan, LIU Lianhui. Application of chaos on spread spectrum communication[J]. Modern Electronic Technique, 2002(6): 60-62.
[9] 张琪, 郑君里. 异步码分多址通信中混沌扩频序列的选择[J]. 电子学报, 2001, 29(7): 865-867.
ZHANG Qi, ZHENG Junli. Choice of chaotic spreading sequences for asynchronous DS-CDMA communication[J]. Acta Electronica Sinica, 2001, 29(7): 865-867.
[10] 菜国梁, 黄娟娟. 超混沌Chen系统和超混沌RLssler系统的异步结构同步[J]. 物理学报, 2006, 55(8): 3997-4004.
CAI Guoliang, HUANG Juanjuan. Synchronization for hyperchaotic Chen system and hyperchaotic RLssler system with different structures[J]. Acta Physica Sinica, 2006, 55(8): 3997-4004.
[11] 郝加波, 张志远. 基于状态观测器噪声干扰的混沌控制与同步[J]. 电子科技大学学报, 2005, 34(5): 618-621.
HAO Jiabo, ZHANG Zhiyuan. Chaotic control and synchronism with noise interference based on state observation[J]. Journal of University of Electronic Science and Technology of China, 2005, 34(5): 618-621.
[12] 王兴元. 混沌系统的同步及在保密通信中的应用[M]. 北京: 科学出版社, 2012: 59-60.
WANG Xingyuan. Chaotic synchronization and its application in security communication[M]. Beijing: Science Press, 2012: 59-60.
[13] 贾飞雷, 徐伟. 一类参数不确定混沌系统的延迟同步[J]. 物理学报, 2007, 56(6): 3101-3106.
JIA Feilei, XU Wei. Lag synchronization for a class of chaotic systems with unknown parameters[J]. Acta Physica Sinica, 2007, 56(6): 3101-3106.
[14] Yassen M T. Controlling chaos and Synchronization for new chaotic systems using linear feedback control[J]. Chaos Soliton & Fract, 2005, 26(3): 913-920.
[15] 王文凯, 孙久勋, 田荣刚. 混沌系统双向耦合同步性的研究[J]. 桂林电子科技大学学报, 2010, 30(4): 298-300.
WANG Wenkai, SUN Jiuxun, TIAN Ronggang. Research on synchronization of mutual coupling in chaotic systems[J]. Journal of Guilin University of Electronic Technology, 2010, 30(4): 298-300.
[16] 朱松盛, 殷奎喜, 刘学军. 差分混沌键控和混沌相位调制相结合的通信系统[J]. 南京师范大学学报(自然科学版), 2010, 33(1): 40-43.
ZHU Songsheng, YIN Kuixi, LIU Xuejun. A differential chaos shift keying chaotic phase modulation combined communication system[J]. Journal of Nanjing Normal University (Engineering and Technology Edition), 2010, 33(1): 40-43.
[17] 朱勇, 王佳楠, 丁群. 新型的CD-DCSK混沌键控保密通信系统[J]. 通信学报, 2012, 33(5): 169-176.
ZHU Yong, WANG Jianan, DING Qun. New kind of CD-DCSK chaos shift keying secure communication system[J]. Journal of Communication, 2012, 33(5): 169-176.
(编辑 陈灿华)
收稿日期:2014-05-11;修回日期:2014-07-21
基金项目(Foundation item):湖南省教育厅科研项目(11C1126)(Project (11C1126) supported by the Education Bureau of Hunan Province)
通信作者:黄乘顺,副教授,从事保密通信研究;E-mail:hcs2011@163.com