不确定时滞系统的约束RMPC容错控制器
刘菁,刘晓华
(鲁东大学 数学与信息学院,山东 烟台,264025)
摘要:在有输入输出约束和执行器故障下,研究一类不确定时滞离散系统鲁棒预测控制容错控制器的分析和设计问题。针对可能发生的执行器增益故障模式,利用线性矩阵不等式方法,给出系统在无外界扰动输入时鲁棒预测控制容错控制器存在的充分条件。当存在外界干扰时,通过引进H∞扰动衰减指标,得到约束鲁棒预测控制H∞容错控制器存在的充分条件。仿真结果表明控制器的有效性。
关键词:不确定时滞系统;容错控制;鲁棒预测控制;执行器故障;输入输出约束
中图分类号:TP273 文献标志码:A 文章编号:1672-7207(2011)S1-0272-05
Constrained RMPC fault-tolerant controller for uncertain delayed systems
LIU Jing, LIU Xiao-hua
(School of Mathematics and Information, Ludong University, Yantai 264025, China)
Abstract: The analysis and design problem of constrained RMPC fault-tolerant controller for a class of uncertain delayed systems with input and output constraints and actuator faults is studied. Based on RMPC algorithm, considering an actuator fault model with gain, using a linear matrix inequality method, sufficient conditions for the existence of constrained RMPC fault-tolerant controller are given for the uncertain delayed system without external disturbances. When there exist external disturbances, by introducing H∞ disturbance attenuation index, sufficient conditions for the existence of constrained RMPC H∞ fault-tolerant controller are obtained. Simulation example shows the effectiveness of the controller.
Key words: uncertain delayed system; fault-tolerant control; RMPC; actuator fault; input and output constraints
对于实际控制系统,时滞和不确定性是普遍存在的,并且它们往往是导致系统不稳定或性能下降的主要原因。因而,对不确定时滞系统的研究是必要 的[1]。考虑到执行器或传感器发生故障对系统性能的影响,不确定时滞系统的容错控制越来越引起人们的注意[2-5]。文献[3]基于一种有学习特性的自适应辨识和控制算法,提出了一种有效的自适应容错控制策略。文献[4]采用L∞可靠控制方法,研究了一类时滞切换系统的容错控制问题。文献[5]针对含有不确定参数的时滞系统,设计了其在执行器故障下的满意容错控制器。然而,这些容错控制方法采用的是全局控制器,不能实时更新控制律以保持系统在时变、干扰等因素影响下实际性能的最优。而且,在控制过程中,这些方法并没有考虑系统的输入输出等硬约束对性能(如稳定性)的影响的局限性。本文作者利用鲁棒预测控制(RMPC)[6]的滚动优化原理,将容错控制器的设计问题转化为通过RMPC算法求取控制器的在线优化问题。在每一采样时刻,通过解决一个有限时域优化问题来得到一系列未来时刻控制量的预测值,但是只实施即时控制量,并且在下一个采样时刻重复整个过程。从优化问题的角度来看,控制问题的再形成为选择所要最小化的性能函数提供了许多自由度,而且,该方法能够有效处理系统变量的静态和动态约束。此外,在输入输出受限的情况下,分别研究了不确定时滞系统在无外界扰动输入以及有H∞干扰衰减指标下基于RMPC的容错控制问题。仿真结果证明了控制器的有效性。
1 问题描述
考虑如下不确定时滞约束系统:




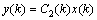
 (1)
(1)
式中:x(k),u(k),w(k),z(k)和y(k)分别表示系统的状态向量、控制输入、外部扰动、被调输出和实际输出,U和Y分别表示输入和输出约束,其中, ,
, 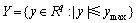 ,d为时滞常数,矩阵对
,d为时滞常数,矩阵对
 ,
,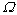 是定义为如下的多包:
是定义为如下的多包:

 ,
, 。
。
假设系统状态可观测,外部扰动能量有界。
考虑如下执行器故障:
 (2)
(2)
其中:uF(k)是故障情况下的执行器输出, 是正常情况下的执行器输出,F=diag[f1, f2, …, fm],
是正常情况下的执行器输出,F=diag[f1, f2, …, fm],  且
且 。引入矩阵F0= diag[f01, f02, …, f0m],G=diag[g1, g2, …, gm],L= diag[l1, l2, …, lm],且|L|=diag[|l1|, |l2|, …, |lm|]。
。引入矩阵F0= diag[f01, f02, …, f0m],G=diag[g1, g2, …, gm],L= diag[l1, l2, …, lm],且|L|=diag[|l1|, |l2|, …, |lm|]。
式中: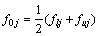 ,
,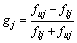 ,
,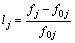 , j=1, 2, …, m,得到执行器增益故障模型:
, j=1, 2, …, m,得到执行器增益故障模型:
 ,
, (3)
(3)
设计含时滞记忆的状态反馈控制器为:
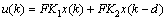 (4)
(4)
则包含执行器故障的闭环系统为:





 (5)
(5)
2 约束RMPC容错控制器
引进如下性能指标:
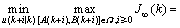
 (6)
(6)


 (7)
(7)
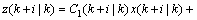

 (8)
(8)

 (9)
(9)

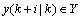
定义二次型函数
 ,其中,P1和P2为对称矩阵,令该函数满足:
,其中,P1和P2为对称矩阵,令该函数满足:
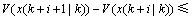
 (10)
(10)
当闭环系统稳定时,必有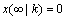 ,
,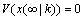 。
。
将式(10)从i=0到i=∞进行叠加,得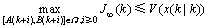 ,即
,即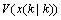 是性能指标值的上界。定义标量
是性能指标值的上界。定义标量 ,并令
,并令
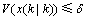 (11)
(11)
则最小化 等价于最小化
等价于最小化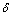 并满足式(11)。
并满足式(11)。
定理1 针对不确定时滞约束系统(1),在执行器故障(3)下,当外部干扰为0时,设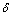 >0,若存在正常数ε1,ε2和ε3以及正定矩阵Q1和Q2,以及矩阵Y1和Y2,满足如下线性矩阵不等式:
>0,若存在正常数ε1,ε2和ε3以及正定矩阵Q1和Q2,以及矩阵Y1和Y2,满足如下线性矩阵不等式:
 (12a)
(12a)
 (12b)
(12b)
 (12c)
(12c)
 (12d)
(12d)
则闭环系统(5)渐近稳定,且
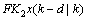 为系统(1)的约束RMPC容错控制器,其中,
为系统(1)的约束RMPC容错控制器,其中, ,
,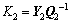 。“
。“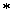 ”表示与对称位置相同分块的转置。
”表示与对称位置相同分块的转置。
证明省略。
3 约束RMPC H∞容错控制器
当系统存在外界干扰且给定扰动衰减指标时,研究时滞不确定约束系统的约束RMPC H∞容错控制器的设计问题。在此只考虑输入约束。
定理2 针对时滞不确定约束系统(1),在执行器故障(3)下,设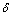 >0,对于给定的干扰衰减指标
>0,对于给定的干扰衰减指标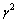 ,若存在正常数ε1,ε2和ε3以及对称正定矩阵Q1和Q2,以及矩阵Y1和Y2,满足如下线性矩阵不等式:
,若存在正常数ε1,ε2和ε3以及对称正定矩阵Q1和Q2,以及矩阵Y1和Y2,满足如下线性矩阵不等式:
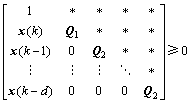 (16a)
(16a)
 (16b)
(16b)
 (16c)
(16c)
 (16d)
(16d)
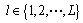
其中: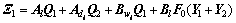 ,
, ,则闭环系统在干扰衰减指标下渐近稳定,且
,则闭环系统在干扰衰减指标下渐近稳定,且
 ,
, ,
,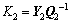 为系统(1)的约束RMPC H∞容错控制器。“
为系统(1)的约束RMPC H∞容错控制器。“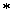 ”表示与对称位置相同分块的转置。
”表示与对称位置相同分块的转置。
4 仿真算例
考虑如下不确定时滞系统:
 ,
, ,
,
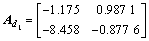 ,
,  ,
,
 ,
, ,
,
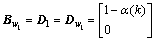 ,
,
 ,
,
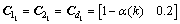 ,
,
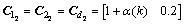 ,
,  为时变不确定参数,d=2为时滞常数。设定系统输入约束为|u|≤6。令L=W=I,R=1,
为时变不确定参数,d=2为时滞常数。设定系统输入约束为|u|≤6。令L=W=I,R=1,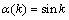 ,初始状态向量
,初始状态向量 ,时滞状态
,时滞状态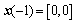 ,
,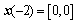 ,控制量u(0)=0。取执行器故障模型F0=0.5,G=0.8。采用本文约束RMPC容错控制器的控制效果如下:
,控制量u(0)=0。取执行器故障模型F0=0.5,G=0.8。采用本文约束RMPC容错控制器的控制效果如下:
w(k)=0即无外界扰动输入,且设定输出约束为 |y|≤4时,仿真结果见图1。
取w(k)为[0,1]分布的高斯白噪声,给定干扰衰减指标γ2=2,仿真结果见图2。
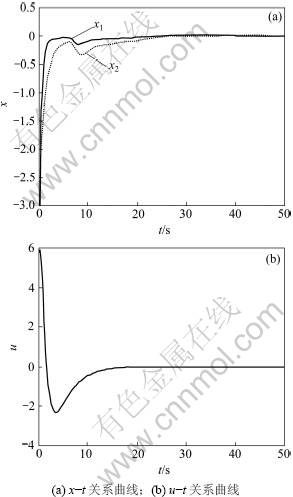
图1 状态x变化曲线和控制输入u曲线
Fig.1 State and input curves
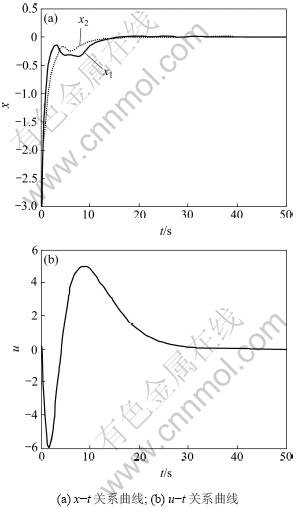
图2 状态x变化曲线和控制输入u曲线
Fig.2 State and input curves
仿真结果表明,当执行器出现故障且输入输出变量受限时,本文的约束RMPC容错控制器在无外界干扰和存在扰动输入2种情况下能够使闭环系统渐近稳定,且满足相应的输入输出约束。
5 结论
本文作者设计了一种时滞不确定系统在输入输出约束下的RMPC容错控制器。利用RMPC 优化算法,针对执行器增益故障,将容错控制器的设计问题转化为RMPC优化问题,以线性矩阵不等式的形式分别给出了系统在无外界扰动输入和在H∞扰动衰减指标下含时滞记忆的约束RMPC容错控制器存在的充分条件。该算法提高了控制过程的实时性和有效性,能够及时克服各种不确定和故障因素的干扰,保持控制效果实际上的最优。仿真结果验证了控制器的有效性。
参考文献:
[1] Richard J P. Time-delay systems: an overview of some recent advances and open problems[J]. Automatica, 2003, 39(10): 1667-1694.
[2] 周东华, Ding X. 容错控制理论及其应用[J]. 自动化学报, 2000, 26(6): 788-797.
ZHOU Dong-hua, Ding X. Theory and applications of fault tolerant control[J]. Acta Automatica Sinica, 2000, 26(6): 788-797.
[3] Diao Y, Passino K M. Intelligent fault-tolerant control using adaptive and learning methods[J]. Control Engineering Practice, 2002, 10: 801-817.
[4] XIANG Zheng-rong, WANG Rong-hao. Robust L∞ reliable control for uncertain nonlinear switched systems with time delay[J]. Applied Mathematics and Computation, 2009, 210(1): 202-210.
[5] 薄翠梅, 王执铨. 不确定时滞系统执行器故障模式下的满意容错控制[J]. 控制与决策, 2009, 24(7): 1013-1017.
BO Cui-mei, WANG Zhi-quan. Satisfactory fault tolerant control for uncertain discrete time-delayed systems against actuator failures[J]. Control and Decision, 2009, 24(7): 1013-1017.
[6] Mayne D Q, Seron M M, Rakovi SV. Robust model predictive control of constrained linear systems with bounded disturbances[J]. Automatica, 2005, 41: 219-224.
[7] 俞立. 鲁棒控制—线性矩阵不等式处理方法[M]. 北京: 清华大学出版社, 2002.
YU Li. Robust control-linear matrix inequality methods[M]. Beijing: Tsinghua University Press, 2002.
(编辑 陈爱华)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:国家自然科学基金资助项目(61174097);山东省自然科学基金资助项目(2009ZRB01521)
通信作者:刘晓华(1959-),男,山东烟台人,博士,教授,从事预测控制、自适应控制理论及应用等研究;电话:0535-6663167;E-mail: xhliu_yt@sina.com