文章编号:1004-0609(2008)09-1680-06
闪锌矿结构AlN、AlP和AlAs的介电和弹性性质的
第一性原理研究
王焕友1, 2,徐 慧1,黄家敏2,张鹏华3
(1. 中南大学 物理科学与技术学院,长沙 410083;
2. 湘南学院 物理系,郴州 423000;
3. 中南大学 材料科学与工程学院,长沙 410083)
摘 要:采用第一性原理赝势平面波方法对闪锌矿结构AlN、AlP和AlAs的电子结构,介电和弹性性质进行计算,结果表明:基于密度函数扰动理论计算的这些材料的介电和弹性性质与其它第一性原理和分子动力学计算值一致性较好,但与实验值之间有一定的差异;晶格参数的优化、赝势的选取和交换关联项的选择都对计算结果有较大影响。根据计算的弹性常数绘制了这些材料特征平面(101)面的弹性模量图,为这方面材料的力学研究提供参考。
关键词:电子结构;玻恩有效电荷;介电张量;弹性常数
中图分类号:O 482;O 472 文献标识码:A
First principle study on dielectric and elastic properties of
zinc-blended AlN, AlP and AlAs
WANG Huan-you1, 2, XU Hui1, HUANG Jia-min2, ZHANG Peng-hua3
(1. School of Physics Science and Technology, Central South University, Changsha 410083, China;
2. Department of Physics, Xiangnan University, Chenzhou 423000, China;
3. School of Material Science and Engineering, Central South University, Changsha 410083, China)
Abstract: With the pseudopotential plane-wave method of first principle, the electronic structure, dielectric and elastic properties of zinc-blende AlN, AlP and AlAs were studied. The results show that based on the density functional perturbation theory, the calculated results are in good agreement with other ab initio and molecular dynamics calculated values, but have definite difference with the experimental data. The calculated values are affected by lattice constant, selection of pseudopotential and selection of exchange-correlation energy. Based on the calculated elastic constant, the elastic moduli of characteristic plane (101) are figured, which offers reference to mechanical study of these materials afterward.
Key words: electronic structure; Born effective charge; dielectric tensor; elastic constant
近年来,闪锌矿结构AlN、AlP和AlAs已得到广泛研究[1?4],由于它们不仅是重要的电子和光电子材料,而且是制作异质结构、超晶格和量子阱的重要成 分[5?6]。研究这些晶体的电子结构、介电和弹性性质,可为半导体新材料的开发提供理论依据和实验指导。由于很难通过化学和物理气相沉积以及高压合成大的高质量单晶,所以关于这些半导体材料的介电和弹性性质的实验数据比较缺乏。为了帮助理解和控制这些材料的介电和弹性性质,理论计算非常重要。近年来,对这些半导体材料的介电和动力学性质已广泛的采用第一性原理进行研究,并结合多种模型和方法进行计算,例如价力模型、绝热键荷模型、刚性离子模型以及冻声子方法、超原胞方法、线性响应方法等。尤其是在1990年后,随着密度函数扰动理论(DFPT)[7?8]的逐步完善,提高了对这些材料性质预测的准确性,且该类计算不需要其它实验值。本文作者基于密度函数理论首先对闪锌矿结构AlN、AlP和AlAs的晶格参数进行优化,然后以优化后的晶格参数运用DFPT计算这些材料的介电和弹性性质。
1 模型和计算方法
基于密度泛函理论,从第一原理赝势平面波方法出发,利用文献[9]中的区域密度近似方法,构造了单电子势中交换关联项,并利用TROULLIER和MARTAIN(TM)方法[10]产生非局域,模守恒赝势,因为这种赝势能生成正确的电荷密度,适合作自洽计算。应用密度函数扰动理论,首先完成结构的完全松弛,接着进行响应函数计算,得到占有态波函数关于原子位移,均匀电场和应变的第一阶微分,最后用这些值计算二阶微分响应函数张量。计算中k空间积分采用Monhorst- Pack[11]方案,将布里渊区按8×8×8的方式划分。电荷密度采用四面体积分方法计算,计算步长为1.36×10?3 eV。
2 结果和讨论
2.1 晶格参数的优化与电子分布
Al、N、P和As的电子结构分别为Ne3s23p1,He2s22p3、Ne3s23p3和Ar4s24p3,此次参与计算的Al价态电子为最外层的3个电子,另外3个元素的价态电子为最外层的5个电子。闪锌矿结构AlN、AlP和AlAs的空间群为F-43M(216),阴离子和阳离子分别以面心立方结构沿对角线1/4套构而成。在本计算之前,首先对其晶格常数进行优化,由于只有一个晶格常数,仅需利用能量最低原理对Monkhorst-Pack格子和截断能作收敛测试。计算得到,其晶格常数分别为4.337、5.448和5.607 ?,将其与实验值4.38[12]、5.465[13]和5.655 ? [14]比较,此次的优化值与其它实验值非常接近,误差仅在1%以内。
基于计算的理论格子值,计算并分别绘出3种化合物半导体沿[111]方向电荷密度分布,如图1所示。在图1中将晶胞对角线作了归一化处理。从图1可以看出,随着阴离子原子序数的增加,原点(阳离子)到对角线1/4阴离子中间的电荷密度减小,这说明随着阴离子原子序数的增加,由于晶格常数的增加和原子电负性的减小,使得离子成分减小,离化度降低,结合力下降。同时,在图中可以看出由于在赝势计算中仅考虑了价态电子,没有包括核电荷,所以在原子核部位几乎没有电荷分布。
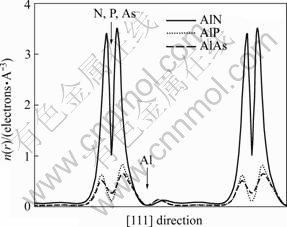
图1 闪锌矿结构AlN, AlP和AlAs沿[111]方向的价电荷密度分布
Fig.1 Line plots of valence-charge density of zinc-blende AlN, AlP and AlAs along [111] direction
基于计算的晶格常数,计算3种化合物半导体的电子态密度,结果如图2所示。从图2可看出,随着阴离子原子序数的增加,其化合物的费密能向低能方向移动,单电子态最高占据轨道和最低未占据轨道的能级差对AlN、AlP和AlAs分别为3.37、1.61和1.25 eV,比实验测定的禁带宽度值 (AlP和AlAs分别为2.50和2.32 eV[15],据本文作者所知,还没有AlN的实验带隙值报道)要小,这是由于用LDA方法求解激发态能量时本身存在的不足,导致理论计算的禁带宽度低于实验值[16]。
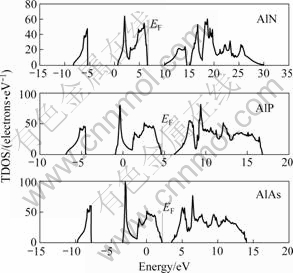
图2 闪锌矿结构AlN, AlP和AlAs的总电子态密度
Fig.2 Total density of states (TDOS) of zinc-blende AlN, AlP and AlAs
2.2 化合物的介电性质
介电常数主要受两个因数影响,一个是电子,另一个是声子。电子对介电常数的影响满足以下关系 式[17]

电子对介电常数的贡献只有在 才变得重要,并存在下列关系式[17]:
才变得重要,并存在下列关系式[17]:

玻恩有效电荷是在外场为零的条件下,由于原子的位移引起的宏观极化的变化与原子位移的比率,可表示为

实际上,玻恩有效电荷是光学声子与电场耦合的结果。同样,玻恩有效电荷可分解为离子和电子的贡献,即

对AlN、AlP和AlAs介电性质的计算共分如下3步完成。
Step 1 Berry相方法作一有限电场下的基态计算,这一步由ABINT[18]软件包执行,得到重要的极化场布洛赫函数。
Step 2 进行线性响应计算得到布洛赫函数的第一阶响应。
Step 3 利用第一阶布洛赫函数线形响应计算介电和玻恩有效电荷张量。
在对3种化合物半导体的介电性质计算中,不仅对波函数的平方余数设定一个最大允许值1×10?20,而且利用两个求和规则检查本次计算关于平面波数及布里渊区k点的选取是否收敛。第一个规则要求玻恩
有效电荷之和为零,即 ;第二个规则要求所有原子在均衡平移条件下具有受力不变性,即
;第二个规则要求所有原子在均衡平移条件下具有受力不变性,即 。由于闪锌矿结构具有立方对称性,对一给定原子,介电矩阵和玻恩有效电荷完全对角化,即沿x、y和z轴分别具有同样的值。比较表1可知,AlN、AlP和AlAs的介电常数均呈增大趋势,这主要是由于其带隙逐步变窄和费密能下降,使得价带顶的电子容易被激发,产生极化,因此,介电常数依次增加。
。由于闪锌矿结构具有立方对称性,对一给定原子,介电矩阵和玻恩有效电荷完全对角化,即沿x、y和z轴分别具有同样的值。比较表1可知,AlN、AlP和AlAs的介电常数均呈增大趋势,这主要是由于其带隙逐步变窄和费密能下降,使得价带顶的电子容易被激发,产生极化,因此,介电常数依次增加。
表1 实验和理论计算的玻恩有效电荷和高频介电常数
Table 1 Calculated and experimental Born effective charge and dielectric constant

用本次的计算值与其它实验值比较发现,玻恩有效电荷被低估而介电常数被高估,这主要是由于本次计算采用的是TM赝势,没有考虑核电子对玻恩有效电荷的贡献。另外,LDA在处理半导体材料时,通常会低估晶格常数,使得声子的本征频率提高,式(2)中的第二项增加。为了说明LDA对介电常数的影响,适当增加晶格常数1%,并采用广义梯度近似(GGA)对玻恩有效电荷和介电常数进行重算。结果显示,LDA对玻恩有效电荷几乎没有影响,但对介电常数的影响比较显著,其值分别为4.52,7.97和9.73,对AlP和AlAs的影响几乎达到4%。比较本次工作的计算值与其它文献[20?22]的理论值发现,一致性较好。
2.3 材料的弹性性质
线性弹性常数通常定义为所受应力与所引起的应变之微分,即 。四阶弹性张量一般拥有
。四阶弹性张量一般拥有
21个独立的张量元,由于闪锌矿结构AlN、AlP和AlAs属于立方晶系,弹性张量减少为3个独立的张量元
C11,C12和C44。闪锌矿结构弹性常数 ,
, ,但C44的计算不如C11和C12的计算那样简单。如果有一个沿[111]轴方向的膨胀,在晶胞内原子的位置不再由对称性所决定,而必须找到作用在原子上的力为零的位置,这样松弛与未松弛的C44不再相等,它们满足Nielsen和Martin关系式[23],即
,但C44的计算不如C11和C12的计算那样简单。如果有一个沿[111]轴方向的膨胀,在晶胞内原子的位置不再由对称性所决定,而必须找到作用在原子上的力为零的位置,这样松弛与未松弛的C44不再相等,它们满足Nielsen和Martin关系式[23],即

由于前都比较符合真实系统,本文作者重点讨论了松弛张量,并在后面的计算中均使用松弛弹性张量。
计算的弹性常数和其它文献的理论和实验值列出在表2中。就本文作者所知,仅有AlAs的实验弹性常数可以利用,比较本文的计算值与文献[24]的布里渊散射测量值,本计算值低于实验值,这主要与本次计算赝势的选取有关,Troullier-Martins赝势是相当软的,因为半核电子没有被明确的处理,而是将它冻结在离子核内,为了定量说明赝势对本次计算的影响,
本文作者采用Hartwigsen-Goedeker-Hutter赝势后重新计算弹性常数,这个赝势将As的3d半核电子作为价电子处理,所要求的收敛比采用Troullier-Martins赝势困难得多,平面波动能截断能达到80 Hartree后总能和力才收敛,采用这种赝势后AlAs的弹性常数依次为110.6、53.8和53.3。
此外,布里渊区的MP网格划分密度也对弹性常数计算精度有一定的影响,当布里渊区的MP网格划分密度增大为16×16×16,弹性常数提高1%左右。
比较本次计算的AlN、AlP和AlAs的弹性常数可知,AlN的弹性常数明显高于AlP和AlAs的弹性常数,而AlP和AlAs相差不大。其原因是由于随着阴离子原子序数的增加,其化合物的晶格常数也随之增加,而阴离子与阳离子之间的电负性之差减小,离子与离子之间的结合力下降,导致3种化合物的弹性常数依次下降。又由于AlN的晶格常数明显的小于AlP和AlAs的晶格常数,但AlP和AlAs的晶格常数相差无几,价电荷密度分布相差不大(见图2)。再者,在P和As赝势的选择中没有考虑内核电荷的差异,因此,AlN的弹性常数明显高于AlP和AlAs的弹性常数,而后两者的值相差不大。
为了更好地说明这些晶体的弹性行为,示意地画出这些材料的弹性模量表征面(见图3)。尽管闪锌矿结构具有高对称性,但不能用一个单一的面来表示整个晶体的弹性行为,实际中非常有用的一个面是表示不同方向弹性模量变化的面。在此,计算3种化合物半导体(101)面的弹性模量,并利用下面公式进行计算[25]

从图中可以看出立方晶系中弹性模量也不是各向同性。随方向的变化取决于 ,这个量在á100?方向为零,在á111?方向达到最大值1/3。矢径直接正比于弹性模量的面,是一个在各面中央凹陷的圆角立方体。到目前为止,还未见有这些材料特征面弹性模量的计算报道。
,这个量在á100?方向为零,在á111?方向达到最大值1/3。矢径直接正比于弹性模量的面,是一个在各面中央凹陷的圆角立方体。到目前为止,还未见有这些材料特征面弹性模量的计算报道。
表2 计算的松弛离子弹性常数
Table 2 Calculated relaxed-ion elastic constant


图3 闪锌矿结构AlN, AlP和AlAs特征面(101)面的弹性模量
Fig.3 Calculated elastic moduli of characteristic plane (101) for zinc-blende AlN, AlP and AlAs
3 结论
1) 采用密度函数理论下的局域密度近似,闪锌矿结构AlN、AlP和AlAs的晶格参数优化值略小于实验值,这主要是局域密度近似的局限所致,并进而影响到理论带隙值。
2) 基于计算的晶格参数优化值,计算所得的这些材料的玻恩有效电荷和介电常数与实验值比较分别被低估和高估,主要与本次计算所采用的赝势和交换关联势有关。
3) 基于计算的晶格参数优化值,采用密度函数扰动理论计算了这些材料的弹性模量,与其它参考文献提供的理论计算值一致性较好,但采用不同的计算模型和赝势会引起微小的差异。
4) 利用计算所得的弹性常数,绘制了这些材料特征平面{101}的弹性模量平面图,尽管还没有实验和理论值作比较,但为今后对这些材料的力学研究提供借鉴。
REFERENCES
[1] WANG H Y, XU H, XIAO J R, LI M J. Electronic structure, dielectric and dynamical properties of zinc-blended AlN from first principles calculation[J]. Mod Phys Lett B, 2007, 21: 1775?1784.
[2] 郝晓静, 党智敏, 徐海萍. 高导热率及低介电常数的AlN/PI纳米复合薄膜研究[J]. 功能材料, 2007, 38(10): 1618?1620.
HAO Xiao-jing, DANG Zhi-min, XU Hai-ping. Research on aluminum nitride/polyimide nanocomposite films with high thermal conductivity and low dielectric permittivity[J]. Journal of Functional Materials, 2007, 38(10): 1618?1620.
[3] 张材荣, 陈宏善, 陈玉红. Al8P8团簇环状结构与性质的密度泛函理论研究[J]. 原子与分子物理学报, 2006, 21(12): 1368?1372.
ZHANG Cai-rong, XU Guang-ji, CHEN Hong-shan, CHEN Yu-hong, LI Wei-xue. Density functional theory study on the structure and properties of Al8P8 clusters[J]. Acta Phys Chim, 2005, 21(12): 1368?1372.
[4] WANG X, VANDERBILT D. First-principles perturbation of dielectric and Born charge tensors in finite electric fields[J]. Phys Rev B, 2007, 75: 115116?115121.
[5] 马 龙, 张 杨, 戴 扬, 杨富华. 高性能InGaAs/AlAs共振隧穿二极管的研制与器件模拟分析[J]. 半导体学报, 2007, 28(4): 563?566.
MA Long, ZHANG Yang, DAI Yang, YANG Fu-hua. Fabrication and device simulation of high performance InGaAs/AlAs resonant tunneling diodes on InP substrates[J]. Chinese Journal of Semiconductors, 2007, 28(4): 563?566.
[6] 熊 焰, 傅正义, 王 皓. CaF2 助剂放电等离子烧结透明AlN陶瓷的微观结构和光学性能[J]. 中国有色金属学报, 2005, 15(11): 1705?1709.
XIONG Yan, FU Zheng-yi, WANG Hao. Microstructure and optical property of transparent AlN ceramics by spark plasma sintering with CaF2[J]. The Chinese Journal of Nonferrous Metals, 2005, 15(11): 1705?1709.
[7] HAMANN D R, WU X, RABE K M, VANDERBILT D. Metric tensors formulation of strain in density-functional perturbation theory[J]. Phys Rev B, 2005, 71: 035117?035129.
[8] WU X, VANDERBILT D, HAMANN D R. Systematic treatment of displacements, and electric fields in density-functional perturbation theory[J]. Phys Rev B, 2005, 72: 035105?035117.
[9] PERDEW J P, ZUNGER A. Self-interaction correction to density-functional approximation for many-electron systems[J]. Phys Rev B, 1991, 23: 5048?5079.
[10] TROULLIER N, MARTINS J L. Effective pseudopotentials for plane-wave caculations[J]. Phys Rev B, 1991, 43: 1991?2006.
[11] HENDRIK J, MONKHORST, PACK J D. Special points for Brillouin-zone intergrations[J]. Phys Rev B, 1976, 13: 5188?5192.
[12] PETROV I, MOJAB E, POWELL R C, GREEN J E, HULTMAN L, SUNDGREN J E. Synthesis of metastable epitaxial zhc-blende-structure AlN by solid-state reaction[J]. Appl Phys Lett, 1992, 60: 2491?2493.
[13] LUCOVSKY G, MARTIN R M, BURSTEIN E. Localized effective charges in diatomic crystals[J]. Phys Rev B, 1971, 4: 1367?1374.
[14] CORSO A D, MAURI F, RUBIO A. Density-functional theory of the nonlinear optical susceptibility: Application to cubic semiconductors[J]. Phys Rev B, 1996, 53: 15638?15642.
[15] MADELUNG O, SCHULTZ M, WEISS H. Physics of group Ⅳ elements and Ⅲ-Ⅴ compounds, of Landolt-B?rnstein, numerical data and functional relationships in science and technology[M]. New York: Springer, 1982: 17?44.
[16] SHANG G, PEACOCK P W, ROBERTSON J. Stability and band offsets of nitrogenated high-dielectric-constant gate oxides[J]. Appl Phys Lett, 2004, 84: 106?108.
[17] GONZE X, LEE C. Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory[J]. Phys Rev B, 1997, 55: 10355?10368.
[18] The ABINIT code is a common project of the Université Catholique de Louvin, Corning Incorporated, and other contributors, URL http://www.abinit.org
[19] GOLDBERG Y. Properties advanced semiconductor materials GaN, AlN, BN, SiC, SiGe[M]. New York: Wiley, 2001: 31?47.
[20] SHIMADA K, SOTA T, SUZUKI K. First-principles study on electronic and elastic properties of BN, AlN, and GaN[J]. J Appl Phys, 1998, 84: 4951?4958.
[21] KARCH K, BECHSTEDT F. Ab initio lattice dynamics of BN and AlN: Covalent versus ionic forces[J]. Phys Rev B, 1997, 56: 7404?7415.
[22] BERNARDINI F, FIORENTINI V. Electronic dielectric constants of insulators calculated by the polarization method[J]. Phys Rev B, 1998, 58: 15292?15295.
[23] NIELSON O H, MARTIN R M. First-principles calculation of stress[J]. Phys Rev Lett, 1983, 50: 697?700.
[24] KRIEGER M, SIGG H. Elastic constants and Poisson ratio in the system AlAs-GaAs[J]. Appl Phys Lett, 1995, 66: 682?684.
[25] NYE J F. Physical properties of crystals their representation by tensors and matrices[M]. Oxford: Clarendon, 1985: 88?101.
基金项目:国家自然科学基金资助项目(50271085)
收稿日期:2007-10-20;修订日期:2008-05-16
通讯作者:王焕友,博士研究生;电话:13975742740;E-mail: whycs@163.com
(编辑 龙怀中)