Control mechanism of a cable truss system for stability of roadways within thick coal seams
来源期刊:中南大学学报(英文版)2017年第5期
论文作者:严红 何富连 李林玥 冯锐敏 邢鹏飞
文章页码:1098 - 1110
Key words:cable truss system; thick coal seam; roof separation; pre-tightening force
Abstract: Cable truss systems have been widely applied in roadways with complicated conditions, such as the large cross-sections of deep wells, and high tectonic stress. However, they are rarely applied to roadways with extremely thick coal seams because the control mechanism of the system for the deformation of the roof and the separation between coal rock segments is not completely understood. By using the relationship between the support system and the roof strata, a mechanical model was established to calculate the deformation of the roof in a thick coal seam with bedding separation under different support conditions: with an anchor truss support and without support. On this basis, the research was used to deduce a method for computing the minimum pre-tightening forces in the anchor truss, the maximum amounts of subsidence and separation with, and without, anchor truss support under the roof, and the maximum subsidence and the decreasing amounts of the separation before and after adopting the anchor truss. Additionally, mechanical relationships between the minimum pre-tightening force and the anchoring force in the anchor were analyzed. By taking a typical roadway with thick coal roof as an example, the theoretical results mentioned above were applied in the analysis and testing of a roof supporting project in a roadway field to verify the accuracy of the theory: favorable experimental results were achieved. In addition, the relationships among other parameters were analyzed, including the minimum pre-tightening forces applied by the anchor truss, the angle of inclination of the anchor cable, and the array pitch. Meanwhile, the changing characteristics of the amounts of roof separation and subsidence with key parameters of the support system (such as array pitch, pre-tightening force, and inclination angle) were also analyzed. The research results revealed the acting mechanism of the anchor truss in control of roadway stability with a thick coal seam, providing a theoretical basis of its application in coal mining.
Cite this article as: YAN Hong, HE Fu-lian, LI Lin-yue, FENG Rui-min, XING Peng-fei. Control mechanism of a cable truss system for stability of roadways within thick coal seams [J]. Journal of Central South University, 2017, 24(5): 1098-1110. DOI: 10.1007/s11771-017-3513-x.
J. Cent. South Univ. (2017) 24: 1098-1110
DOI: 10.1007/s11771-017-3513-x
YAN Hong(严红)1, HE Fu-lian(何富连)2, LI Lin-yue(李林玥)3, FENG Rui-min(冯锐敏)4, XING Peng-fei(邢鹏飞)1
1. Key Laboratory of Deep Coal Resource Mining, Ministry of Education of China
(School of Mines, China University of Mining & Technology), Xuzhou 221116, China;
2. Faculty of Resources and Safety Engineering, China University of Mining and Technology (Beijing),
Beijing 100083, China;
3. Guizhou Xinlian Blasting Engineering Group Co., Ltd., Guiyang 550002, China;
4. Department of Mining and Mineral Resources Engineering, Southern Illinois University,Carbondale, Illinois 62901, USA
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract: Cable truss systems have been widely applied in roadways with complicated conditions, such as the large cross-sections of deep wells, and high tectonic stress. However, they are rarely applied to roadways with extremely thick coal seams because the control mechanism of the system for the deformation of the roof and the separation between coal rock segments is not completely understood. By using the relationship between the support system and the roof strata, a mechanical model was established to calculate the deformation of the roof in a thick coal seam with bedding separation under different support conditions: with an anchor truss support and without support. On this basis, the research was used to deduce a method for computing the minimum pre-tightening forces in the anchor truss, the maximum amounts of subsidence and separation with, and without, anchor truss support under the roof, and the maximum subsidence and the decreasing amounts of the separation before and after adopting the anchor truss. Additionally, mechanical relationships between the minimum pre-tightening force and the anchoring force in the anchor were analyzed. By taking a typical roadway with thick coal roof as an example, the theoretical results mentioned above were applied in the analysis and testing of a roof supporting project in a roadway field to verify the accuracy of the theory: favorable experimental results were achieved. In addition, the relationships among other parameters were analyzed, including the minimum pre-tightening forces applied by the anchor truss, the angle of inclination of the anchor cable, and the array pitch. Meanwhile, the changing characteristics of the amounts of roof separation and subsidence with key parameters of the support system (such as array pitch, pre-tightening force, and inclination angle) were also analyzed. The research results revealed the acting mechanism of the anchor truss in control of roadway stability with a thick coal seam, providing a theoretical basis of its application in coal mining.
Key words: cable truss system; thick coal seam; roof separation; pre-tightening force
1 Introduction
Bolt support technique for stability of roadways has been widely employed in coal mines [1]. However, many roadways are under complicated conditions, such as excavated within thick coal seams, a large cross-section, and high tectonic stress. In addition, factors such as the density of the surrounding rock, the stress on the structural plane, and coal permeability also influence the stability of the surrounding rocks [2]. Apart from these factors, limitations in the length, pre-tightening force, and shear strength of bolt support decrease the extent of any control over roadways of this kind [3, 4]. As a result, deformation and even roof fall accidents frequently occur during supporting operations or the service of roadway, thus leading to casualties and financial loss. A roadway with thick coal roof was taken as an example, as it includes many complicated factors such as its large cross-section during excavation, the composition of its roof included a thick coal seam and thin soft partings therein, and well-developed joint fissures in the coal seam. Under these conditions, when bolt support system is adopted during excavation, the roof separation layer of the roadway expands over a large area, and then subsides suddenly. In consequence, part of the roadway loses stability and a collapse occurs [5]. However, the cable truss system, due to its preferable support structure, roof controlling properties, and convenient construction procedure, affords significant restraint to the complex surrounding rock masses in a coal mine [6, 7].
The cable truss system has a simple structure and consists of two inclined anchor cables, a connector, and two locksets. As shown in Fig. 1, one side of the anchor cable is anchored by a resin anchoring cartridge in a stable stratum where the roof and the side rib of the roadway intersect. The other side passes through the connector to be fixed by the lockset on the central surface of the roadway roof after the application of a large pre-tightening force [8]. Thereby, the shallow part of the roof excavated is under a stressed state and is therefore stabilized [9]. Actually, the cable truss system was developed from the bolt truss which was initially used in underground mines in the late of 1960s. A bolt truss is mainly composed of inclined bolts, tie beams, and other components [10].

Fig.1 Mining of close seams and layout of roadway
On the basis of a large number of experiments conducted on bolt trusses in the field, anchor bolts have been gradually improved and their construction and installation have become more convenient. In addition, bolt truss systems for different structures have been proposed for adaptation to the roadway roof under different geological conditions [11]. The bolt truss system is mainly divided into two types: the Birmingham truss and in-cycle truss, the differences lie in the different installation times and locations as they deliver the requisite horizontal force [12].
To reveal the control mechanism of the bolt truss for the roof, many methods have been applied, such as, photoelastic simulation, similar material simulation, field measurements, mechanical calculations, and so on. By adopting photoelastic simulation techniques, NEALL et al [13, 14] found that the bolt truss system can form compressive stress zones in the roof so as to reduce the shear failure risk therein. This is beneficial to the control of separation in the roof strata. GAMBRELL et al [15] proposed that the strata between the inclined bolts are compressed; while strata on the roof-side wall angle are under tension. By using the method of similar material simulation, KHAIR [16] discovered that on one hand, the bolt truss can control deformation and destruction of the roof subjected to tension; on the other hand, it strengthens the shear strength near the roof strata under excavation. COX et al [17] found the bolt truss can form a pressure arch in the roof strata and is capable of stiffening the roof strata. STANKUS et al [18] believed that the bolt truss imposed a bidirectional force to the roof strata both from the horizontal direction and vertical direction. Therefore, its roof controlling effect is much better compared to a bolt support, which can only impose unidirectional force in the vertical direction. Besides, the bidirectional force contributes to the control of the shear failure of the stratum in the roof-side wall angle of the roadway. SEEGMILLER et al [19] discovered that bolt trusses have significant controlling effects on the horizontal displacement of the roof and tested this effect in Dutch Creek Mines. LIU et al [20, 21] analyzed the transverse resistance of the anchor bolt in the bolt truss system and deduced the relationships between the pulling force of the rod, the transverse resistance of the anchor bolt, and the reinforcement. Afterwards, the maximum and minimum pre-tightening force of the pull rod and minimum anchorage force of the anchor bolt were calculated and analyzed. Meanwhile, tests were conducted in typical roadways. ZHU et al [22] calculated the minimum force on, and length of, the bolt truss on a given horizontal level by mechanical means. GHABRAIE et al [23] proposed several indices reflecting the control of the roof using a bolt truss and simulated the controlling effects of the bolt truss on a stratified roof. O’GRADY et al [24] predicted the load applied to the truss and discussed those factors influencing its behaviour. As to research into bolt truss systems, field experiments were mainly carried out in roadways with complex conditions (e.g. compound mudstone roof, large section in a deep well, high tectonic stress). Meanwhile, the merits and demerits of anchor trusses and bolt trusses were compared and their supporting theories were explored to some extent [25, 26].
Most of studies mentioned above focused on the bolt truss system, while little research has concentrated on cable truss systems, especially, for the thick coal roof control of the roadways and large excavation. Because of no stable anchoring point in a bolt truss support and the weak coordination of the bolt-anchor support, accidents induced by instability occur frequently upon separation of layers of the roadway roof [27, 28]. However, as the support mechanism of the cable truss system for roadways with thick coal roof has not been studied completely, its wider application has been impeded. Therefore, studying the mechanism of the cable truss system for the separation and deformation of thick coal roof, factors influencing the stability of the support system of the surrounding rocks in zones with thick coal roof, and their inter-relationships are important in the case of separation already occurring in the roadway. Furthermore, it helps to provide a theoretical basis for the design parameters of an anchor truss, and therefore guarantees the security and stability of the support for roadways with thick coal roof.
2 Behaviour of a cable truss system in roadways with thick coal roof
2.1 Controlling effects of cable truss system: bedding separation and roof deformation
Due to the complicated geological conditions, such as the presence of several weak and soft parting layers in the thick coal roof, with large disparity of physico- mechanical properties, and the large cross-section of these types of roadway, roadways with thick coal roof differs a lot from those in other mines. However, the locations of bedding separation are changing, influenced by many factors such as rock strata structures, horizontal stress, mining conditions, supporting style, etc. Therefore, during excavation and support, bedding separation and even overall deformation are likely to happen between the coal seam and parting layer. This research analyzed the effectiveness of a cable truss system in controlling the amount of separation and deformation in the roof strata and the reduction thereof. As shown in Fig. 2, suppose that the anchoring point of the anchor cable in the cable truss system is fixed at layer n+1 (a stable stratum). There was no subsidence during the support process while bedding separations occurred between layers m and m+1, n and n+1. The separating layers (strata m and m+1) which were close to the excavated roadway were analyzed. In this research, the span of the roadway was 2l, with 2a between portholes, and the inclined angle of the anchor cable in the system was α.
According to the relationship between the support system and the roof strata, a mechanical model of the cable truss system in a thick coal roof was established. As shown in Fig. 3, the array pitch of the cable truss system is c; the anchoring force of the anchorage section on one side of the anchor cable is F; the vertical load on the inclined section of the anchor cable applied by the roof strata is between k1q1 and k1qn, where k1 is the vertical pressure coefficient in the inclined section of the cable truss system imposed by the strata. The horizontal load is between λk1q1 and λk1qn, in which λ represents lateral pressure coefficient of the strata; the friction imposed on the slant anchor cable within the strata is F1, and the friction on a horizontal section of one side of the anchor cable is F2; the thicknesses of each stratum and slanting length of the support in the strata, respectively, are between h1 and hn, as well as l1 and ln.
As shown in Fig. 3, the calculation formula of
friction imposed on the slant anchor cable within the strata (F1) and the anchoring force on the cable truss system (F) were obtained:
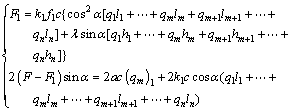 (1)
(1)
where f1 is the friction coefficient between the inclined section of the anchor cable and the roof strata. The required anchoring force on the cable truss system is then
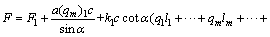
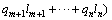 (2)
(2)
The inclined anchor cable in the cable truss system penetrated several related roof strata, therefore, after applying a large pre-tightening force, strata under the separation layers became approximately equivalent to a composite beam. Here, the section formed by the combination of all these strata was treated as an equivalent section with a homogenous material and analyzed accordingly. According to the plane bending assumption, the longitudinal linear strain at point y in the cross-section is [29]
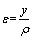 (3)
(3)
where y is the distance between the neutral axis and the longitudinal layer and ρ is the radius of curvature of the neutral axis.

Fig.2 Cable truss system supporting a roadway with a thick coal roof
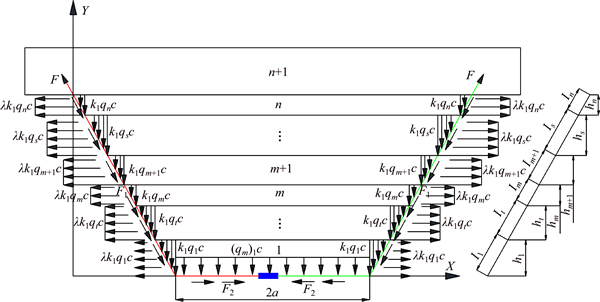
Fig.3 Mechanical model of cable truss system in a thick coal roof
Suppose that each longitudinal section is under a unidirectional state of stress. When the normal stress in the composite beam is within the proportional limit of each stratum, the bending normal stresses from section 1 to section g are
 (4)
(4)
Owing to the fact that no axial force exists in the cross-section of each layer and the bending moment M is the only limiting condition, the following equation is obtained:
 (5)
(5)
By substituting Eq. (4) into Eq. (5), we get
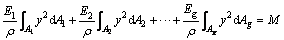 (6)
(6)
Therefore, the curvature of the neutral axis layer is given by
 (7)
(7)
Then, the section of the composite stratum is converted to an equivalent section of the strata material in the first layer; the practical elastic modulus is therefore equivalent to the elastic modulus of the first layer, namely 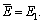 The flexural rigidity of the section in the composite structure is
The flexural rigidity of the section in the composite structure is 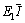 , and the centroid of the composite beam lies at
, and the centroid of the composite beam lies at
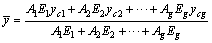 (8)
(8)
Let t be any layer between 1 and g, and the moment of inertia of this layer is
 (9)
(9)
where At is the longitudinal cross-sectional area of layer t, and at represents vertical distance between the centerline of the section in layer t and that of the composite beam. The equivalent moment of inertia under these conditions is
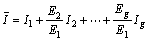 (10)
(10)
where yc1, yc2, …, ycg are the positions of the centroids of each layer of the composite beam.
The force imposed on the roadway roof by the cable truss system includes the pre-tightening force and the anchoring force. The subsidence of the roof and changes in the separation layer are mainly controlled by the pre-tightening force [30, 31]. Here, the support function of the cable truss system applied on the roof is converted into an uplift of its horizontal part. Suppose that the minimum pre-tightening force is F3. Therefore, the support function of the cable truss system imposed on the roof can be expressed as
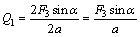 (11)
(11)
To analyze the controlling effects of the cable truss system on roof separation and deformation, roof strata with and without separations were studied separately. It should be noted that here, the roof strata below, and including, the nth layer was analyzed.
1) The mechanical model of the strata without separation, and within the supporting scope of the cable truss system, is shown in Fig. 4.
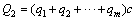 (12)
(12)
Then, the differential equations of the deflection in different strata intervals are given by
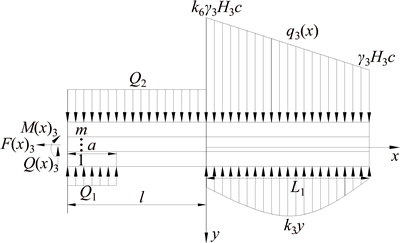
Fig.4 Mechanical model of cable truss system used to support strata on one side
 (13)
(13)
Among them,  is the torque of layers m+1 to n.
is the torque of layers m+1 to n.
Equation (13) gives
 (14)
(14)
where β3 is the characteristic coefficient, given by 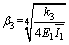 .
.
According to the boundary conditions at x=0 and continuity conditions between intervals, the following results are obtained:
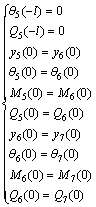 (15)
(15)
By combining Eqs. (13), (14) and (15), A5, B5, C5, D5, A6, B6, C6, D6, C7 and D7 were calculated. Therefore, the maximum subsidence from layer 1 to m after applying the support of a cable truss system is
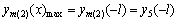 (16)
(16)
2) The mechanical model of the strata with separation (from layer m+1 to layer n) within the supporting scope of the cable truss system is demonstrated in Fig. 5.
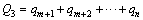 (17)
(17)

Fig.5 Mechanical model of cable truss system used to support strata on one side
The differential equations of the deflection in different strata intervals are
 (18)
(18)
where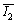 is the torque in layers m+1 to n.
is the torque in layers m+1 to n.
When 0
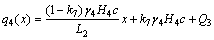 (19)
(19)
At x=L2, the subsidence of the roof reaches a certain value, which can be obtained according to the mechanics of a semi-infinite body resting on an elastic foundation beam:
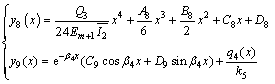 (20)
(20)
where β4 is the characteristic coefficient given by  .
.
Based on the boundary conditions at x=-l and continuity conditions between intervals, the following results are acquired:
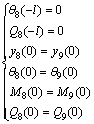 (21)
(21)
By combining Eqs. (18), (19), (20) and (21), A8, B8, C8, D8, C9 and D9 were obtained. Therefore, the maximum subsidence within the scope of the cable truss system is
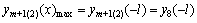 (22)
(22)
By combining Eqs. (16) and (22), the maximum value of the separation of the roof after adopting the support of a cable truss system is
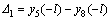 (23)
(23)
2.2 Relationship between minimum pre-tightening force in cable truss system and anchoring force in inclined anchor cable
By applying the pre-tightening force, the cable truss system is able to form a prestressed bearing structure with a certain rigidity, which can significantly decrease the destructive influence of tensile stress on the roof strata. Because the inclined anchor cables on both sides of the cable truss system are symmetrical, one half of them can be used in any force analysis, as shown in Fig. 6.
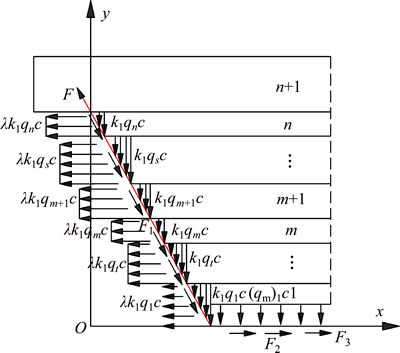
Fig.6 Mechanical model of anchor cable on one side of cable truss system
The horizontal friction on the anchor cable on one side of the cable truss system is
 (24)
(24)
where f2 is the coefficient of friction between the horizontal part of the anchor cable and the strata. At equilibrium (in the horizontal direction), the following results are obtained:
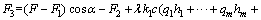
 (25)
(25)
The relationship between the minimum pre- tightening force in the cable truss system and the anchoring force is
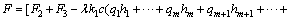
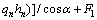 (26)
(26)
2.3 Roof separation and deformation after excavation of an unsupported roadway with thick coal roof
To compare the support effect of a cable truss system for a roadway roof, an unsupported excavated roadway was studied. A mechanical model of the first layer and layer m+1 in an unsupported roof was established. As shown in Fig. 7, γ1 and γ2 are the average bulk unit weights of the strata from the roof and from layer m to the ground strata, respectively; H1 and H2 are the distances from the ground surface to the roadway roof and to layer m, respectively; k2 and k4 are the stress concentration coefficients in the first layer and layer m+1; k3 and k5 are coefficients describing the elastic foundation on the coal side and layer m, respectively, and s is the unsupported distance. Mechanical analysis of first layer and layer m+1 (where i is one of the strata within the roof) gave the following differential equations:
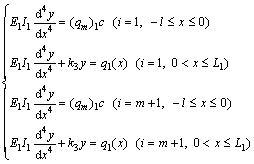 (27)
(27)
Equation (27) shows the amount of subsidence in different intervals of the first layer and layer m+1 layer in the roof:
 (28)
(28)
where β1 and β2 are characteristic coefficients:

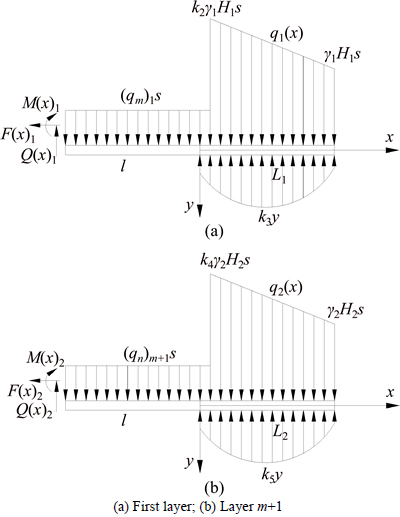
Fig.7 Mechanical models of first layer and layer m+1 on an unsupported roof:
As the loads born by the first layer and layer m+1 are already close to the strength of the rock at x=L1 and x=L2, based on the semi-infinite principle of elastic foundation beams, we get
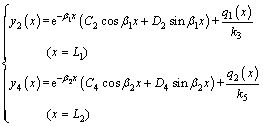 (29)
(29)
According to the boundary conditions at x=-l, and continuity conditions between intervals, the following results are acquired:
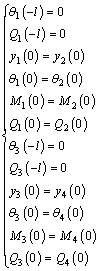 (30)
(30)
By combining Eqs. (27), (28), (29) and (30), A1, A2, A3, B1, B2, B3, C1, C2, C3, D1, D2 and D3 are calculated. According to the theory of composite beams, because layers 1 to m are in a state of compatible deformation, the maximum deformation of layer m can be calculated. Similarly, the maximum deformation of layer m+1 is
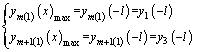 (31)
(31)
According to Eq. (31), the maximum separation layer between layers m and m+1 is
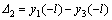 (32)
(32)
Based on the aforementioned analysis, the maximum variation in roof separation and subsidence before, and after, the application of a cable truss system are determined as follows:
(1) By combining Eqs. (16) and (31), the maximum variation in subsidence on the roadway roof is
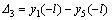 (33)
(33)
(2) By combining Eqs. (23) and (32), the maximum variation in the roof separation on the roadway is
 (34)
(34)
3 Case study analysis
Case 1: A mining roadway within the 12.39 m thick coal seam, excavated within the primary mineable coal seam No. 9 of a coal mine located in Shanxi Province, was studied. Top coal caving is adopted at the working face and the parameters of each stratum on the roadway are shown in Fig. 8. The location of roof separation was monitored between the fourth, and fifth layers. The average bulk unit weight of the roof strata is γ=25 kN/m3; the friction coefficients in the inclined and horizontal directions of the cable truss system are f1=f2=0.3. The vertical stress coefficient is k1=0.7. The elasticfoundation coefficient when the coal is regarded as the foundation is k3=1.5×108 N/m2, and distance from the initial point at which the abutment pressure is applied on the side coal to the roadway is L1=12 m. The elastic foundation coefficient when the fourth layer is regarded as the foundation is k5=2.2×108 N/m2, and the distance from the initial point at which the abutment pressure is applied on this layer to the roadway is L2=9 m. The stress concentration factors of each layer on the roof surface are 2.8, 2.0, 2.1 and 1.9, respectively.

Fig. 8 Coal seam and rock strata columnar section
The anchor terminal of the inclined anchor cable in the cable truss system was anchored in the stable stratum of the eighth layer with key parameters as follows: inclination angle of the anchor cable of 70°, an array pitch of 1 m, and a distance between portholes of 2.4 m. By combing Eqs. (16), (23), (26), (31) and (32), Eq. (35) is obtained, into which, the aforementioned parameters are substituted:
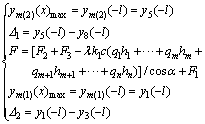 (35)
(35)
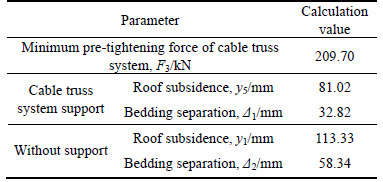
Seen from Table 1, calculated results showed that the maximum subsidence and bedding separation of the roof, were 81.02 mm and 32.82 mm with support, and 113.33 mm and 58.34 mm without support, which can verify the accuracy of the above theory.
Table 1 Calculated results of roof of roadways with cable truss system and without support
Case 2: The working face No. 5203 of a coal mine in Shanxi Province is shown in Fig. 9. The average thickness of the primary mineable coal bed is 14.27 mm, where 2-3 parting layers with 0.1-0.38 m thick on the average for each is embedded. The above rock layers nearby are respectively 2.19 m thick sandy mudstone and 1.62 m thick gritstone. Combined support from bolts and anchor cables was adopted along the haulage roadway, which is 5.3 m in width. Five roof fall accidents occurred during its excavation: the maximum length, width, and height of the roof falls were 18 m, 5 m and 8 m, respectively. The open-off cut is rectangular (width××3.5 m). Owing to the particularly large width, roof falls will continue to happen and thereby cause heavy casualties if combined support from both bolts and anchor cables is not adopted.

Fig. 9 Layout of No. 5203 working face
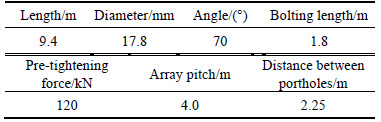
On the basis of the combined support from bolts and anchor cables, the cable truss system was added. Meanwhile, the parameters of the cable truss system were optimized so as to determine the support parameters, as shown in Table 2.
According to results of the field test, the roof separation in the roadway was not more than 35 mm, and the roof deformation was less than 95 mm. In addition, from the onset of excavation to the service stage, no roof fall accidents occurred in the roadway.
Table 2 Support parameters of cable truss system
4 Factors influencing stability of rocks surrounding a roadway in a thick coal seam with support of a cable truss system
Generally speaking, many factors influence the stability of the rocks surrounding a roadway in a thick coal seam under the support of a cable truss system: the properties of surrounding rock, the thickness of the coal, the density of the coal seam, number of mezzanine levels, etc all play a part. In fact, on the basis of the geological conditions, the key parameters affecting the cable truss system (array pitch, inclination angle, pre-tightening force, etc) are the major factors influencing the stability of the surrounding rocks in a thick coal seam.
1) Relationships between maximum roof deformation and inclination angle of the anchor cable, array pitch, and distances between portholes when a cable truss system is applied.
Figure 10 shows that: (1) with a constant inclination angle of the cable truss system, array pitch, and the
maximum roof subsidence are in proportion to each other; while when the array pitch remains constant, with an increase in inclination angle, the maximum roof subsidence increases slightly. (2) At certain sections of the roadway during the supporting process of the cable truss system, near the center of the roadway, the roof underwent a large displacement while the further the position from the central part of the roof, the lower the deformation. (3) When the inclination angle of the cable truss system changes, as shown in Fig. 10(c), the deformation differs slightly along the roadway roof: for an inclination angle of 45°, at a point 0.4 m to the right of the roadway, the maximum roof subsidence is 78.57 mm; while the maximum roof subsidence is 79.95 mm at a point 2.3 m to the right. Moreover, with an increase in the angle, the increasing range of the maximum roof subsidence decreases. When the inclination angle of the roof increases from 75° to 85°, the subsidence increases by only 0.04 mm. (4) The distance between portholes exerts little influence on the overall roof deformations: in the same position, when the porthole separation increases from 1.2 m to 1.6 m, the roof deformation increases by 0.016 mm; as the porthole separation increases from 0.8 m to 1.0 m, the deformation increases by 0.007 mm.
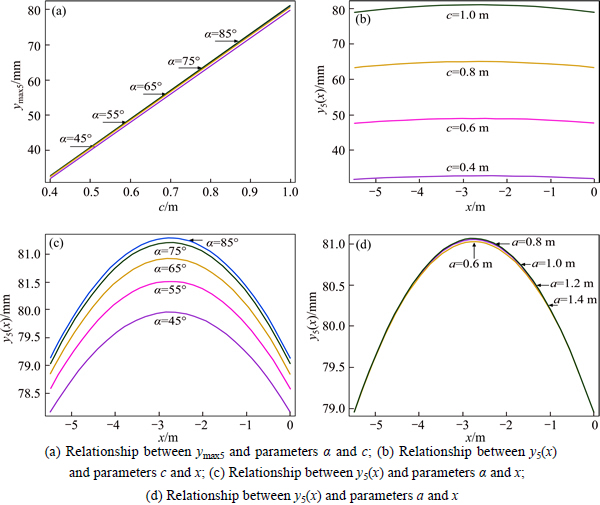
Fig. 10 Relationships of maximum roof subsidence (y5(x)) and array pitch (c), inclination angle of anchor cable (α) in cable truss system and distance between portholes (a):
2) Relationships between maximum roof deformation, separation, and unsupported distance under unsupported conditions
As shown in Fig. 11, without the cable truss system, the amount of roof deformation and separation increases linearly as the unsupported distance increases; when the unsupported distance increases from 0.5 m to 1.0 m, maximum deformation and separation increased separately from 57.32 mm and 29.30 mm, to 112.50 mm and 58.27 mm, respectively. As with the cable truss system, in some sections, the maximum value of the roof deformation was greatest in the center of the roadway, and was relatively small when near each side. Moreover, with an increasing unsupported distance, the changes became more obvious, as did those of the maximum roof separation.
3) The relationships between the maximum roof deformation, separation, inclination angle of the anchor cable, and the array pitch of the system before, and after, application of a cable truss support system
Figure 12 shows that: (1) with increasing array pitch in the cable truss system, the maximum roof subsidence and separation gradually differed more significantly before and after the support was installed. Besides, the subsidence and separation were mainly concentrated on the central part of the roadway and decreased dramatically compared with their unsupported values. When the array pitch of the support system was 1 m, the roof deformation and separation were reduced, respectively, by 31.26 mm and 26.70 mm. Therefore, the support system was superior. (2) With a decreased anchor
angle, the roof subsidence and separation gradually increased, and the range over which it increased was closely related to the changed in inclination angle. For example, at a point 2.8 m to the right of the roof, when the inclination angle decreased from 85° to 75° and from 65° to 55°, the maximum changes in separation and subsidence increased by 0.17 mm and 0.05 mm, and 0.41 mm and 0.39 mm, respectively.
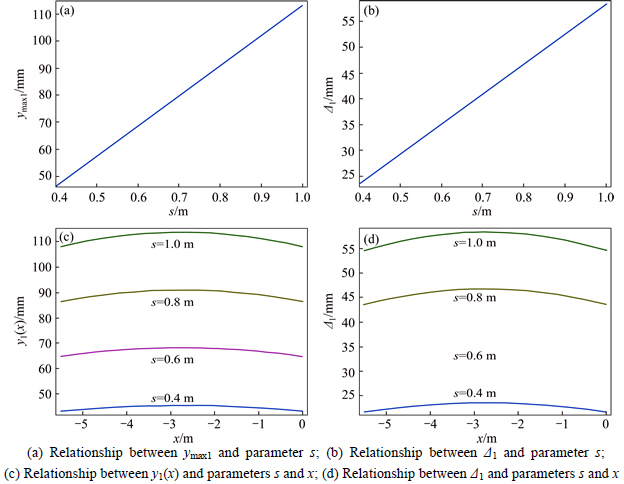
Fig. 11 Relationships of array pitch of unsupported distance (s), roadway span (x), and maximum roof subsidence (y1(x)), and maximum roof separation (△1):
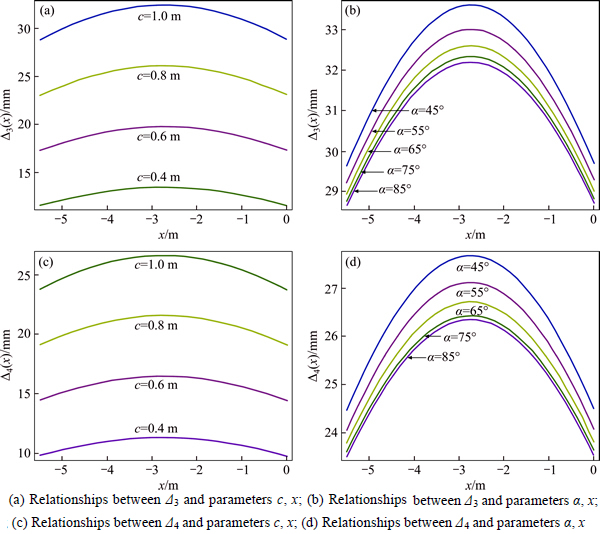
Fig. 12 Relationships of array pitch of cable truss system (c), roadway span (x), and maximum change in roof subsidence (△3) and separation (△4) before and after cable truss system installation:
4) Relationships of array pitch, minimum pre- tightening force on cable truss system, and inclination angle of anchor cable therein
As shown in Fig. 13, (1) with a constant porthole separation in the cable truss system, with an increase in the array pitch, the minimum pre-tightening force applied by the system had to increase accordingly. However, when the array pitch remains constant, changes in porthole separation exerted little influence on the magnitude of the pre-tightening force. (2) The inclination angle of the anchor cable in the support system and its variation significantly influenced pre-tightening force, namely u1=△F3/△c. As the inclination angle increased from 45° to 75°, the value of u1 changed; whereas, when it increased from 75° to 85°, the change was less obvious.
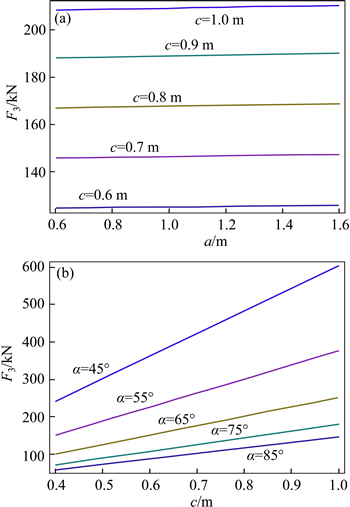
Fig. 13 Relationships of array pitch of cable truss system (c), porthole separation (a) and inclination angle (α) of anchor cable, and minimum pre-tightening force (F3)
5 Conclusions
1) On the basis of the relationship between the cable truss system and the roof strata in the mining roadway with a thick coal seam, mechanical models for the roadway with its thick roof under the support of a cable truss system, and unsupported, were established. Thereafter, formula for calculating the minimum pre-tightening force, the maximum roof subsidence and bedding separation in the cable truss system were derived, and the relationship between the pre-tightening force and the anchorage force, and relationships of the unsupported distance and the maximum subsidence and separation without support were also investigated.
2) The formula for computing the decrease in the maximum roof subsidence and separation before, and after, the application of a cable truss system was derived. The formula provides a theoretical basis for the application of such cable truss systems in roadway roof with thick coal seam. By using this formula on a typical mine roadway with a thick coal seam roof, and by testing the cable truss system in situ, the stability of the system was verified and favorable control thereof was achieved.
3) According to analysis of the parameters of the cable truss system which was applied to support a thick coal seam roof, the array pitch, inclination angle, and pre-tightening force of the anchor truss exerted significant influences on roof stability; the array pitch was proportionally related to the maximum subsidence; with an increased array pitch, and a decreased inclination angle and pre-tightening force, the maximum deformation and separation increased gradually; when the inclination angle increased, the changes in roof subsidence and separation increased, and the range thereof was closely related to the changes in inclination angle; when the array pitch increased, the corresponding minimum pre-tightening force also increased.
References
[1] BRADY B, BROWN E. Rock mechanics for underground mining (3rd edition) [M]. Dordrecht: Kluwer Academic Publishers, 1985: 312-320.
[2] YAN Hong, ZHANG Ji-xiong, LI Lin-yue, FENG Rui-min. Stability assessment of rock surrounding an I-beam supported retreating roadway [J]. Journal of Central South University, 2015, 22(9): 3598-3607.
[3] XIE Sheng-rong, LI Er-peng, LI Shi-jun, WANG Jin-guang, HE Chong-chong, YANG Ya-feng. Surrounding rock control mechanism of deep coal roadways and its application [J]. International Journal of Mining Science and Technology, 2015, 25(3): 429-434. (in Chinese)
[4] GONG Feng-qiang, LI Xi-bing, GAO Ke. Catastrophe progression method for stability classification of underground engineering surrounding rock [J]. Journal of Central South University: Science and Technology, 2008, 39(5): 1081-1087. (in Chinese)
[5] UNVER B, YASITLI N E. Modeling of strata movement with a special reference to caving mechanism in thick seam coal mining [J]. International Journal of Coal Geology, 2006, 4(3): 227-252.
[6] LI Jian-ping, HE Fu-lian, YAN Hong, JIANG Hong-jun. The caving and sliding control of surrounding rocks on large coal roadways affected by abutment pressure [J]. Safety Science, 2012, 50(4): 773-777.
[7] YAN Hong, HE Fu-lian, XU Teng-fei. Study on double-cable-truss controlling system for large section coal roadway of deep mine and its practice [J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(11): 2248-2257. (in Chinese)
[8] HE Fu-lian, YIN Dong-pin, YAN Hong. Study on the coupling system of high prestress cable truss and surrounding rock on a coal roadway [C]// Rock Stress and Earthquakes - Proceedings of the 5th International Symposium on In-Situ Rock Stress. Beijing, 2010: 643-646.
[9] YAN Hong, HE Fu-lian. A new cable truss support system for coal roadways affected by dynamic pressure [J]. International Journal of Mining Science and Technology, 2012, 22(9): 613-617.
[10] SHEOREY P, VERMA B, SINGH B. An analysis of the roof truss [J]. Journal of Mines, Metals and Fuels, 1973, 21(8): 233-236.
[11] GHABRAIE B, REN G, GHABRAIE K, XIE Yi-min. A study on truss bolt mechanism in controlling stability of underground excavation and cutter roof failure [J]. Geotechnical Geological Engineering, 2013, 31(2): 667-682.
[12] GAMBRELL S, CRANE P. Support characteristics of classic and in-cycle trusses (a photoelastic comparison) [C]// Rock Mechanics: Key to Energy Production, Proceedings of the 27th US Symposium on Rock Mechanics. Tuscaloosa, AL, USA, 1986: 505-511.
[13] NEALL G M, HAYCOCKS C, TOWNSEND J M. Influence of some critical design parameters on roof truss support capacity: A preliminary report [C]// Rock Mechanics Applications in Mining. New York, USA, 1977: 228-233.
[14] NEALL G M, HAYCOCKS C, TOWNSEND J M, JOHNSON L P. Optimizing roof truss installations with body-loaded photoelastic models [J]. Min Eng, 1978, 30(5): 660-666.
[15] GAMBRELL S, HAYNES C. In-situ roof trusses vs. angle roof bolts, a photoelastic comparison [J]. Trans Soc Min Eng AIME, 1970, 247(2): 109-110.
[16] KHAIR A W. Physical and analytical modeling of the behavior of truss bolted mine roofs [C]// Rock Bolting: Theory and Application in Mining and Underground Construction. Abisko, Sweden, 1984: 125-142.
[17] COX R M, COX M. Design and application of the mine roof truss system in the Illinois coal basin [C]// Proceedings of the First Conference on Ground Control Problems in Illinois Coal Basin. Carbondale, IL, USA, 1978: 124-135.
[18] STANKUS J C, GUO S, MCCAFFERY J J. Innovative concept in tailgate entry support: Elimination of crib blocks through utilization of new high-capacity roof truss systems [J]. Mining Engineering, 1996, 48(9): 57-62.
[19] SEEGMILLER B, REEVES J. Truss performance at Dutch Creek Mine, Colorado Colliery guardian Redhill [J]. Colliery Guardian Redhill, 1990, 238(6): 164-166.
[20] LIU B, YUE Z, THAM L. Analytical design method for a truss-bolt system for reinforcement of fractured coal mine roofs: Illustrated with a case study [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(2): 195-218.
[21] LIU Bo, LI Xian-wei, TAO Long-guang. Analysis on lateral behavior of bolts in roof truss system [J]. Chinese Journal of Geotechnical Engineering, 1998, 20(4): 36-39. (in Chinese)
[22] ZHU F, YOUNG D S. Analysis of roof truss for underground support [C]// Geo-Engineering for Underground Facilities. ASCE, 1999: 507-513.
[23] GHABRAIE B, REN G, GHABRAIE K. Effects of thickness of roof layers on optimum design of truss bolt system using finite element modeling techniques [J]. Electronic Journal of Geotechnical Engineering, 2013, 18A: 147-158.
[24] O’GRADY P, FULLER PG. Design considerations for cable truss secondary supports in roadways of underground collieries [C]// Proceedings of the 11th International Conference on Ground Control in Mining. Wollongong, 1992: 240-248.
[25] LIU Bo, TAO Long-guang, LI Xian-wei. Development and application of bolt truss in layer roof [J]. Coal Science and Technology, 1999, 27(7): 34-36. (in Chinese)
[26] LI Gui-chen, ZHANG Nong, LIU Zhao-hui, KAN Jia-guang. Prestress truss bolt support technology for coal roadway [J]. Journal of Mining & Safety Engineering, 2007, 24(2): 150-154. (in Chinese)
[27] KUSHWAHA A, SINGH S K, TEWARI S. Empirical approach for designing of support system in mechanized coal pillar mining [J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(7): 1063-1078.
[28] YAN Hong, ZHANG Ji-xiong, DING Zi-wei, HUANG Yan-li. Surrounding rock deformation mechanism of roadways with extra-thick coal seam [J]. Disaster Advances, 2013, 6(S6): 226-233.
[29] OU Gui-bao, ZHU Jia-ming. Mechanics of material [M]. Harbin: Harbin Engineering University Press, 1997: 93-97. (in Chinese)
[30] ZHAO Hong-liang, YAO Jing-ming, HE Fu-lian. Application of prestress truss cable in large cross section coal roadway [J]. Journal of China Coal Society, 2007, 32(10): 1061-1065. (in Chinese)
[31] ZHANG Nong, GAO Ming-shi, XU Xing-liang. Pretentioned supporting system of roadway and its engineering application [J]. Journal of Mining & Safety Engineering, 2002, 12(4): 1-4. (in Chinese)
(Edited by YANG Bing)
Cite this article as: YAN Hong, HE Fu-lian, LI Lin-yue, FENG Rui-min, XING Peng-fei. Control mechanism of a cable truss system for stability of roadways within thick coal seams [J]. Journal of Central South University, 2017, 24(5): 1098-1110. DOI: 10.1007/s11771-017-3513-x.
Foundation item: Project(51404248) supported by the National Natural Science Foundation of the Youth Science Foundation of China; Project(2017XKQY012) supported by Fundamental Research Funds for the Central Universities of China; Project(2014M551702) supported by the China Postdoctoral Science Foundation; Project supported by the Priority Academic Program Development (PAPD) of Jiangsu Higher Education Institutions, China
Received date: 2015-09-16; Accepted date: 2016-03-22
Corresponding author: YAN Hong, Associate Professor, PhD; Tel: +86-516-83593019; E-mail: linodex@163.com

