DOI: 10.11817/j.issn.1672-7207.2019.02.010

基于OpenFOAM重力式采样器自由下落姿态数值分析

马哲¹，孔丹雅¹，王胤²，翟钢军¹

(1. 大连理工大学 海岸及近海工程国家重点实验室，辽宁 大连，116024；

2. 大连理工大学 岩土工程研究所，辽宁 大连，116024)

摘要：为了提高深水重力式沉积物采样器在海流、缆绳等外力作用下的采样效率，基于OpenFOAM程序并通过动态重叠网格方法，模拟静水中采样器在触底前较大范围内自由下落时的姿态。首先构建采样器与流体相互作用三维时域耦合计算模型，并采用Newmark法对结构在流场中的运动方程进行迭代求解；验证网格收敛性，分别对初始倾角为0°和5°的采样器自由下落姿态进行时域模拟，分析下落距离、下落速度以及采样器偏转角之间的相互关系并研究采样器的偏转角对取样效率的影响。研究结果表明：本文构建的结构与流体相互作用的三维时域计算模型可以精确模拟采样器自由下落姿态；采样器的初始偏转角对采样器下落姿态以及取样效率均有较大影响。

关键词：重力式沉积物采样器；自由下落姿态；流固相互作用；OpenFOAM程序；重叠网格

中图分类号：P751             文献标志码：A         文章编号：1672-7207(2019)02-0321-07

Simulation analysis of free falling posture of gravity sampling device using OpenFOAM

MA Zhe¹, KONG Danya¹, WANG Yin², ZHAI Gangjun¹

(1. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China;

2. Institute of Geotechnical Engineering, Dalian University of Technology, Dalian 116024, China)

Abstract: In order to improve sampling efficiency of gravity sampler in deep water under complicated environment conditions such as sea current and cable, the free falling posture of sampler among a wide range before its grounding was simulated based on OpenFOAM program and dynamic overset grid method. Three-dimensional time-domain coupled calculation model of the sampler which interacts with flow field was established. The Newmark method was used to solve the motion equations of the structure iteratively in the flow field. After verification of the grid convergence, the free falling postures of sampler with initial slant angle of 0° and 5° were simulated and the relationships among falling distance, falling speed and slant angle of the sampler were analyzed. In the end, the influence of the slant angle on the sampling rate was studied. The results show that the proposed three-dimensional time-domain coupled calculation model can predict the free falling posture accurately. The initial slant angle has great influence on falling posture and sampling rate of sampler.

Key words: gravity sediment sampler; free falling posture; fluid-structure interaction; OpenFOAM program; overset grid

近年来，深海资源探测技术向高精度、大深度、近海底和原位方向发展，勘探与识别、保真取样技术、资源范围圈定和资源量有效评价研究是深海海底矿产资源勘查技术的发展趋势和重点^[1]。目前，深水重力式沉积物采样器已经成为深海勘测中的重要设备，它获取的海床表层土样对海底矿产资源勘探、海洋工程地质勘察、科学研究、国家权益维护、军事应用等都有重要意义^[2]。重力式采样器主要依靠自身质量下落并贯入土中取得沉积物样本，因其工作原理简单、成本较低、对辅助设备要求不高，适用于水深为800~6 000 m的深海泥沙沉积物的取样。但是，重力式采样器对贯入土体前的下落姿态尤其是触底时候的倾角比较敏感，直接影响海床沉积物取样质量与取样器的安全。重力活塞式取样器^[3]是目前使用范围最广的深海沉积物取样装置，代表产品有美国WHOI(Woods Hole Oceanographic Institution)研制的Giant Piston Corer，Jumbo Piston Corer和 Long Coring以及法国IFRTP(French Institute for Austral Research and Technology)研制的CALYPSO取样器。其中，CALYPSO取样器作为当今世界上取样长度最长的取样装置，获取了长为64.5 m的深海沉积样品，但其系统最大自身质量也超过了10 t^[4]。我国从20世纪70年代开始研制沉积物取样设备。在已有简单重力取样器设计原理的基础上，宋欢龄等^[5]研制了一种安全重力活塞取样器。经过四五十年的发展，采样器结构及操作方法不断被改进。补家武等^[6]从海底取样的意义和取样器的分类入手, 阐述了海底取样器的发展现状及其工作原理；张庆力等^[7]使用FLUENT软件对采样过程进行了模拟仿真，发现在下落高度足够大时，采样器撞击海底的速度趋于稳定；CHEN等^[8]提出了采样器刀头切割泥土时的能量消耗公式，杜星等^[3]在此基础上完善了贯入深度的计算公式；文泽军等^[9]通过对重力式采样器冲击系统进行建模和数值计算，分析了其取样性能和影响贯入深度的因素，如配重、冲击高度、取样管直径、沉积物特性等。2013年，我国利用自己设计的重力活塞取样器采得了长度达10.9 m的柱状样品^[10]。重力式采样器目前存在如下问题：自身质量过大、样品保真度不高，特别是在使用过程中受海流、船舶漂移、地形起伏等因素的影响，容易在入土时过度倾斜甚至拖倒，这些问题在深海水域尤为突出，会导致采样效果不理想甚至影响使用安全^[11-13]。采样器在触底前的自由下落过程中，伴随着较复杂的外部荷载条件及尾流影响。处理此类流体与较大范围内运动的结构之间的相互作用问题，通常采用数值模拟，模型实验及实地测量等研究手段。其中，针对深水重力式采样装置的模型实验往往受场地限制较大，无法在适当比例条件下开展；实地测量成本及不确定因素较多，通常不能进行系统研究。而采用基于计算流体力学方法的开源程序OpenFOAM对采样器自由下落过程中的姿态进行实时数值模拟，其结果可以较真实地反映采样器的动力特性。在OpenFOAM程序中，常用的动网格方法有网格随体变形法、滑移网格法等，但只有重叠网格能够较好地适应物体多自由度、大变形运动^[14]，因此，最初被应用于航空航天领域中空气动力学研究^[15]。BOGER等^[16]最先在OpenFOAM程序中实现了重叠网格方法。近年来，重叠网格也被应用于海洋工程方面。曹洪建等^[17]利用重叠网格建立了三维数值水池，具有较高的精度；CHANDAR^[18]在OpenFOAM平台中利用三维非结构化动态重叠网格验证了运动物体的流场变化情况；王建华等^[19]采用OpenFOAM 和重叠网格技术获得了船舶不同工况下的阻力、侧向力和转首力矩的时程曲线，验证了采用当前处理方法数值求解纯摇首运动的可靠性。综上所述，重力式采样器的采样成功率并不高，常出现样品长度无效甚至样品数据丢失的情况。目前研究者的研究主要集中在贯入过程中采样器与土体的相互作用及保真率等方面，而对采样器触底前自由下落阶段初始边界条件及采样器下落姿态等因素研究较少。因此，本文作者基于OpenFOAM程序，采用重叠网格技术，对深海重力式采样器在不同初始边界条件自由下落阶段的姿态进行模拟，研究下落距离、触底时采样器倾斜角度等因素对采样效率的影响，以期节省采样时间与成本，提高采样效率。

1  基本理论

1.1  数值方法

对于不可压缩黏性流体，控制方程为连续性方程及动量方程(Navier-Stokes方程)，其表达式如下：

　      　　     (1)

     (2)

式中：u和P分别为流体速度和压力矢量；t为时间；ρ和υ分别为流体密度与运动黏度，本文中水的密度ρ=1 000 kg/m³，υ=1.0×10^{-6 m2}/s；为梯度算子。

本文采用k-ε湍流模型来研究湍流的影响，当流动不可压，且不考虑源项时，定义湍动能k与耗散率ε的输运方程为^[20]

 (3)

 (4)

式中：x_i和x_j为坐标分量；u_i和u_j为速度分量；μ为分子黏性系数；μ_k为湍动黏度；G_k为湍动能k的产生项；各常数C_1ε=1.44，C_2ε=1.92，C_μ=0.09，σ_k=1.0，σ_ε=1.3。

采用Newmark方法求解运动方程。给定初始值u₀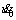，和，确定时间步长Δt 和参数α和β，由

           (5)

 (6)

即可求得t+Δt时刻的物体的位移、速度、加速度。重复以上过程，就可得到整个时间段内的物体的位移、速度和加速度。其中，β取0.25，即采用线性加速度法。

1.2  极限速度

采样器在海水中下落时主要的作用力有重力、浮力和海水拖曳力。由于近海底处海流速度几乎为0 m/s，所以，暂不考虑横向的海流力作用。其中，采样器的重力减去其在水中所受的浮力为有效重力G_y(又称浮容重)。

           (7)

式中：G为自重力；F为浮力；V为采样器的体积；m为采样器质量；g为重力加速度。

拖曳力类似于绕流阻力，故拖曳力F_D可以按绕流阻力计算^[21]：

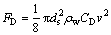             (8)

式中：d_s为采样器直径；ρ_w为海水密度，取值为1.028×10³kg/m³；C_D为采样器在海水中的拖曳阻力系数；A_F为采样器面积；v为采样器在海水中的下落速度。随着采样器速度增大，其阻力也将增大。由此得出下落速度v与下落距离x的关系式为^[22]

  (9)

式中：v₀为初速度；；；为采样器的密度。当下落高度足够大即x→∞时，采样器的重力与阻力将达到平衡，即达到极限速度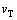^[23]

           (10)

1.3  贯入深度

贯入深度取决于海底的硬度和取样器的结构形状与配重，取样器整个运动过程可看作是不同能量间的转换，遵循能量守恒原理。考虑重力势能、动能、内壁摩擦作功、外壁摩擦作功和刀头切割作功，暂不考虑拖拽力作功。根据能量守恒，从取样器初始接触沉积物至取样器贯入最大深度并静止，能量方程为

E_p+E_k-W_i-W_o-W_c=0          (11)

式中：E_p为重力势能；E_k为动能；W_i为取样管内壁摩擦所作的功；W_o为取样管外壁摩擦作功；W_c为刀头切割所作的功。

杜星等^[24]的研究表明：在确定采样器质量、内外直径、摩擦因数等参数后，即可确定入土前速度与贯入深度的关系：

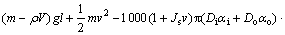
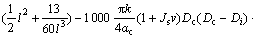
       (12)

式中：l为贯入深度；α_c为刀头摩擦因数；α_i为内壁摩擦因数；α_o为外壁摩擦因数；J_s为侧壁黏滞阻尼因子；D_o为外壁直径；D_i为内壁直径；D_c为刀头外径；θ为刀头交角。

1.4  重叠网格

重叠网格算例需要2部分网格：第1块是包围物体的贴体网格，第2块是正交的背景网格。圆柱网格嵌套在背景网格之中。2块网格之间相互独立，在拓扑结构上没有约束关系。贴体网格可以在背景网格之中任意移动。在整个计算过程中，尽管物体产生了大幅度的位移，但2块网格并没有发生变形，仅仅是2个网格的相对位置发生了变化^[15]。

进行重叠网格计算首先需要进行洞单元搜寻，即将在计算域之外的网格标记为洞单元，并排除在流场计算之外。之后需要给插值边界单元从另一块网格中搜寻贡献单元，即背景网格的插值边界单元需要从圆柱网格中搜索贡献单元，圆柱网格的插值边界单元需要从背景网格中搜索贡献单元。在计算插值系数和优化重叠区域后，即可进行数值计算。

2  数值模拟验证

2.1  网格收敛性验证

为了验证重叠网格计算的准确性，首先对形状较为简单的球体在水中的自由下落进行数值模拟，参照文献[25]建立模型，如图1所示。

图1  球体模型及网格划分

Fig. 1  Sphere model and grid partition

图1中球体半径为0.04 m，密度为7 850 kg/m³，球体外部为长×宽×高为0.2 m×0.2 m×0.2 m的贴体网格。最外层还有水槽计算域，水平向2个维度均为0.5 m，竖直方向为8 m，计算域的6个面均为壁面边界。水槽和物体表面均采用光滑无滑移壁面边界条件(wall)，物体网格采用重叠网格(overset)。流体动力黏度系数为1.003×10^-3 Pa·s。针对上述模型，研究不同网格边长下球体在静水中自由下落速度随时间的变化，不同网格边长及其结果对比见表1。

从表1可以看出：随着网格数量增加，A2和A3数值模拟得到的阻力系数与文献[26]中的实验结果(阻力系数为0.429 8)差别较小。球体模型的网格数较少，且为静水中的自由下落，但从具体的计算时间来看，A2网格的计算时间约为32 h，而A3达到57 h。可以预计，在后期进一步研究中，对于结构更复杂、网格数更多的采样器模型，计算耗时将进一步增加。因此，文中在保证计算准确性的同时，考虑到计算资源的限制，选取算例 A2 中的网格作为计算网格。不同网格边长下的球体速度变化见图2。由图2可知：球体在下落过程中速度不断增大，总体结果过程与式(9)的理论结果一致。

表1  不同网格边长数值模拟结果对比

Table 1  Comparison of simulation results of meshs with different sizes

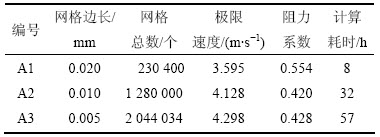
图2  不同网格边长下的球体速度变化

Fig. 2  Change of the sphere velocity in different meshs

2.2  采样器自由下落的数值模拟

采样器实际工作中一般分为3个阶段：从船舶下放至水中的入水过程；在缆绳牵引及海流作用等环境条件的约束下落过程；下落至距离海底一定高度时，取样器自由下落直至接触海底的过程。本文借助重叠网格方法进行数值模拟，重点对采样器自由下落过程进行运动响应分析。此外，海流主要作用于牵引下落阶段的缆绳，使得采样器在自由下落阶段开始时产生倾角，而自由下落阶段时处于接近海底的深海环境中，此时的海流的作用较弱。因此，本文设置采样装置在静水中自由下落。

为进一步验证数值模拟的准确性，采样器的数值模型参考文献[8]中的重力式采样器参数设计，总质量为1.5 t，取样管长为4 m，外径为105 mm，中部有配重块以增加采样器自身的质量。使用ICEM软件建立简化的模型并划分网格，如图3所示。

图3  重力式采样器模型及网格划分

Fig. 3  Model of gravity sampler and grid partition

由文献[8]可知：重力式采样装置下落的初速度为0 m/s，在近海底处经过约12 m的自由下落过程后贯入土中，仿真参数与实际实验条件较吻合。将采样器下落过程中速度与位移的模拟计算结果与文献[8]中已有的实测结果进行对比分析，如图4所示。

由图4可知：约1.25 s后，采样器的下落距离为6 m，速度达到9 m/s。实测数据中采样器在约1.6 s时触底产生了回弹，加速度的方向发生改变，而数值模拟中未考虑触底情况，即采样器一直处于自由下落过程，因此，仅比较自由下落部分速度和位移的变化。

从图4还可以看出：位移和速度对比结果相差不大。实测中采样器具有整流罩，能够调节尾流，在一定程度上减小阻力，而数值模型中简化了结构较复杂的整流罩部分，因此，其速度和位移略均比实测值小。

图4  采样器位移和速度随时间的变化

Fig. 4  Change of displacement and velocity of sampler with time

在不考虑触底的情况下，本文构建的方法能够较好地模拟重力式采样器在静水中自由下落的过程，且数值结果与实测结果吻合较好。而且由于采样器的自身质量较大，接触海底时具有足够的重力势能使其贯入土中，故对下落速度即动能基本没有要求。因此，在理想的垂直下落情况下，采样器可以完成取样任务。

2.3  采样器倾斜下落过程分析

在理想状态下，采样器在脱缆自由下落时是垂直的，但在实际使用中，由于海流、船舶漂移等影响，很难保证采样器不出现偏转角，而初始的倾斜角对最终取样效率的影响尚不明确，因此，在垂直下落的基础上，模拟采样器倾斜下落的过程具有重要的意义。根据前人海测经验，在较良好的海况条件下，通过对下落速度的控制，采样器的晃荡并不十分剧烈，倾角一般在0°~10°之间。本文作者在进行数值计算时，选取采样器倾角为5°进行分析，采样器下落过程中姿态变化及速度云图如图5所示。采样器偏转角度和速度随时间的变化见图6。

图5  采样器下落过程中姿态变化及速度云图

Fig. 5  Posture changes and velocity cloud charts of falling sampler

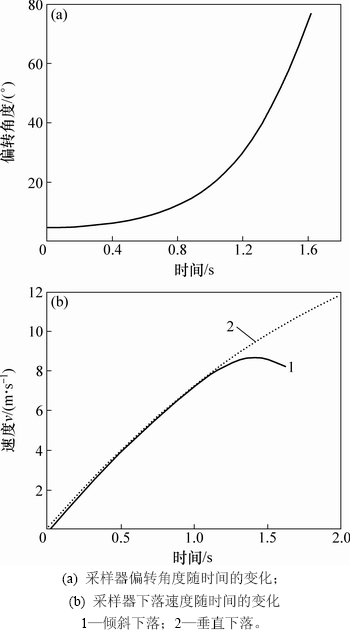
图6  采样器偏转角度及下落速度随时间的变化

Fig. 6  Change of angle and velocity of sampler with time

由图6可知：采样器的偏转角度在下落过程中几乎呈指数增长，在下落1.36 s时采样器偏转已达45°，此时，下落距离为7.02 m。而采样器下落速度呈线性增大，在1.41 s时下落速度达到峰值8.73 m/s，随后开始减缓；同时，在下落1.41 s后采样器偏转角为44.5°，此时，采样器垂直于速度的横截面投影已经较大，受到的阻力也相对较大，从而使得阻力对采样器产生的影响超过重力的影响，因此，采样器下落速度开始减小。

在实际测试中，期望获取的沉积物样本能够覆盖更深的土层，因此，在设计阶段一般要求采样器入土前的偏转角尽量控制在较小范围内。采样器倾斜入土示意图如图7所示。将取样率定义为入土垂直深度d_th与取样管长度l的比值。触底时的偏转角与取样率的关系如表2所示。从表2可知：当采样器以5°初始倾斜角下落时，该采样器如果要保证90%以上的取样率，下落距离不能超过5 m，容许的最大偏转角约为25°。

图7  采样器倾斜入土示意图

Fig. 7  Diagram of slant sampler penetrating in ground

表2  倾斜采样器偏转角与取样率的关系

Table 2  Relationship between deflection angle and sampling rate

3  结论

1) 本文采用的重叠网格法运算过程稳定，能够获得球体下落速度变化规律及达到极限下落速度时匀速下落的稳定状态，且数值模拟结果与实测结果较接近，说明重叠网格法是解决流体与较大范围运动结构相互作用问题的一种有效方法。

2) 在实际海测中，采样器在自由下落时的初始倾斜角对取样率影响很大。与初始边界条件为垂直下落状态相比，其下落速度呈先增大后减小的趋势；对于采样器在5°初始倾斜角的情况下，偏转的角速度可达34 (°)/s。

3) 自由下落距离也是影响采样效率的重要因素。距离过长，采样器失稳程度越高，导致采样失败甚至造成采样器损伤。采用本文采样器，在保证90%采样率的前提下,下落距离不能超过5 m。

参考文献：

[1] 何高文. 向深海资源开发强国进军[EB/OL]. [2016-09-15]. http://www.gtzyb.com/lilunyanjiu/20160918_99784.shtml.

HE Gaowen. Advance to deep water resources power[EB/OL]. [2016-09-15]. http://www.gtzyb.com/lilunyanjiu/20160918_ 99784.s html.

[2] 阮锐. 海底重力取样技术的探讨[J]. 海洋测绘, 2009, 29(1): 66-69.

RUAN Rui. Discussion of technology on sea floor gravity sampling[J]. Hydrographic Surveying and Charting, 2009, 29(1): 66-69.

[3] 杜星, 孙永福, 胡光海, 等. 重力活塞取样器贯入深度研究[J]. 海洋工程, 2016, 34(3): 133-139.

DU Xing, SUN Yongfu, HU Guanghai, et al. Study on penetration depth of gravity piston corer[J]. The Ocean Engineering, 2016, 34(3): 133-139.

[4] 黎永发. 深海沉积物取样器及其球阀关键技术的研究[D]. 杭州: 浙江大学海洋学院, 2016: 4-7.

LI Yongfa, Research on the key technology of deep-sea sediment sampler and ball valves[D]. Hangzhou: Zhejiang University. College of Ocean, 2016: 4-7.

[5] 宋欢龄. 安全重力活塞取样器: CN 87209127 U[P]. 1988-02-17.

SONG Huanling. Safe gravity piston sampler: CN 87209127 U[P]. 1988-02-17.

[6] 补家武, 鄢泰宁, 昌志军. 海底取样技术发展现状及工作原理概述——海底取样技术专题之一[J]. 探矿工程(岩土钻掘工程), 2001, 44(2): 44-48.

BU Jiawu, YAN Taining, CHANG Zhijun. Introduction to the status quo and operating principle of seabed samplers: part Ⅰ of the subject on seabed sampling[J]. Exploration Engineering (Rock & Soil Drilling and Tunneling), 2001, 44(2): 44-48.

[7] 张庆力, 刘贵杰, 刘国营. 新型海底沉积物采样器结构设计及采样过程动态分析[J]. 海洋技术, 2009, 28(4): 20-23.

ZHANG Qingli, LIU Guijie, LIU guoying. The structural design and dynamic analysis of collecting process of new type seabed sampler[J]. Ocean Technology, 2009, 28(4): 20-23.

[8] CHEN Jiawang, FAN Wei, BINGHAM B, et al. A long gravity-piston corer developed for seafloor gas hydrate coring utilizing an in situ pressure-retained method[J]. Energies, 2013, 6(7): 3353-3372.

[9] 文泽军, 刘湛, 金永平, 等. 深海重力活塞取样器取样系统波动力学建模与分析[J]. 中国机械工程, 2016, 27(17): 2280-2286.

WEN Zejun, LIU Zhan, JIN Yongping, et al. Modeling and analysis for sampling system of deep-sea gravity piston sampler based on wave mechanics[J]. China Mechanical Engineering, 2016, 27(17): 2280-2286.

[10] 程振波, 杨刚, 吴永华,等. 长重力活塞取样器在鄂霍茨克海的应用[J]. 海洋科学进展, 2013, 31(4): 553-558.

CHENG Zhenbo, YANG Gang, WU Yonghua, et al. Application of long gravity piston corer in the Okhotsk Sea[J]. Advances in Marine Science, 2013, 31(4): 553-558.

[11] 李民刚. 40米重力活塞取样器设计及仿真[D]. 青岛: 青岛理工大学机械工程学院, 2012: 3-11.

LI Mingang. Design and simulation of 40 m gravity piston corer[D]. Qingdao: Qingdao University of Technology. College of Mechanical Engineering, 2012: 3-11.

[12] WINTERS W J, LORENSON T D, PAULL C K. Coring and gas hydrate-related operations during the IMAGES VIH/PAGE 127 gas hydrate and paleoclimate cruise on the RV Marion Dufresne in the Gulf of Mexico[R]. Woods Hole, USA: Woods Hole Science Centre, 2002: 4-43.

[13] 张鑫, 栾振东, 阎军, 等. 深海沉积物超长取样系统研究进展[J]. 海洋地质前沿, 2012, 28(12): 40-45.

ZHANG Xin, LUAN Zhendong, YAN Jun, et al. A　review of development in deep-sea long coring system[J]. Marine Geology Frontiers, 2012, 28(12): 40-45.

[14] 刘垚, 蔡卫军, 王明洲. 基于重叠网格方法的水轮机非定常水动力数值仿真[J]. 中国舰船研究, 2018, 13(1): 85-92.

LIU Yao, CAI Weijun, WANG Mingzhou. Numerical simulation for hydrodynamic performance of marine current turbine based on overset grid[J]. Chinese Journal of Ship Research, 2018, 13(1): 85-92.

[15] 沈志荣. 船桨舵相互作用的重叠网格技术数值方法研究[D].上海: 上海交通大学船舶海洋与建筑工程学院, 2014: 13-16.

SHEN Zhirong. Development of overset grid technique for hull-propeller-rudder interactions[D]. Shanghai: Shanghai Jiao Tong University. School of Naval Architecture, Ocean & Civil Engineering, 2014: 13-16.

[16] BOGER D A, NOACK R W, PATERSON E G. Dynamic overset grid implementation in OpenFOAM[C]// 5^th OpenFOAM Workshop. Gothenburg, Sweden, 2010: 21-24.

[17] 曹洪建, 万德成. 基于naoe-FOAM-SJTU求解器构建三维数值波浪水池[J]. 复旦学报(自然科学版), 2013, 52(5): 627-634.

CAO Hongjian, WAN Decheng. Three-dimensional numerical wave tank based on naoe-FOAM-SJTU solver[J]. Journal of Fudan University(Natural Science), 2013, 52(5): 627-634.

[18] CHANDAR D. Seamless integration of an overset grid framework for OpenFOAM:[EB/OL].[2015-09-24]. https://ww w.esi-group.com/abstract-openfoam2015-chandar-institute-high-performance-computing-seamless-integration-overset-grid.

[19] 王建华, 万德成. 基于重叠网格技术数值模拟船舶纯摇首运动[J]. 水动力学研究与进展(A辑), 2016, 31(5): 567-574.

WANG Jianhua, WAN Decheng. Numerical simulation of pure yaw motion using dynamic overset grid technology[J]. Journal of Hydrodynamics(A), 2016, 31(5): 567-574.

[20] 张晓东, 张培林, 傅建平, 等. k-ε双方程湍流模型对制退机内流场计算的适用性分析[J]. 爆炸与冲击, 2011, 31(5): 516-520.

ZHANG Xiaodong, ZHANG Peilin, FU Jianping, et al. Applicability analysis of k-ε turbulence models on numerical simulation of internal flow field of recoil brake[J]. Explosion and Shock Waves, 2011, 31(5): 516-520.

[21] BROWN P P, LAWLER D F. Sphere drag and settling velocity revisited[J]. Journal of Environmental Engineering, 2015, 129(3): 222-231.

[22] 张君元, 杨光复. 重力活塞采样器海上采样技术的研究[J]. 海洋科学, 1983, 7(6): 19-22.

ZHANG Junyuan, YANG Guangfu. Gravity piston sampler sampling technology research at sea[J]. Marine Sciences. 1983, 7(6): 19-22.

[23] 董天宏, 黄海科, 柯鹏飞. 鱼雷锚的方向稳定性研究[J]. 广东造船, 2015, 34(4): 24-27.

DONG Tianhong, HUANG Haike, KE Pengfei. Directional stability of torpedo anchors[J]. Guangdong Shipbuilding, 2015, 34(4): 24-27.

[24] 杜星, 孙永福, 宋玉鹏, 等. 重力活塞取样器贯入模型研究[J]. 海洋科学进展, 2018, 36(1): 88-97.

DU Xing, SUN Yongfu, SONG Yupeng, et al. Study of penetration depth from a model of gravity piston corer[J]. Advances in Marine Science, 2018, 36(1): 88-97.

[25] 张雪琪. 动力贯入锚水中自由下落过程的数值模拟[D]. 大连:大连理工大学建设工程学部, 2015: 14-17.

ZHANG Xueqi. Numerical simulation of the free fall of gravity installed anchor in water[D]. Dalian: Dalian University of Technology. Faculty of Infrastructure Engineering, 2015: 14-17.

[26] 刘君, 张雪琪. 板翼动力锚水中自由下落过程数值模拟[J]. 海洋工程, 2017, 35(3): 29-36.

LIU Jun, ZHANG Xueqi. Numerical simulation of the installation of gravity installed plate anchors in water[J]. The Ocean Engineering, 2017, 35(3): 29-36.

(编辑  伍锦花)

收稿日期：2018-04-16；修回日期：2018-06-16

基金项目(Foundation item)：国家自然科学基金资助项目(41572252)(Project(41572252) supported by the National Natural Science Foundation of China)

通信作者：王胤，博士，副教授，从事深海地质勘探及采样技术研究；E-mail：y.wang@dlut.edu.cn