基于流固耦合的泥水盾构隧道施工引发地表变形

邓宗伟¹，伍振志²，曹浩³，沈平欢²

(1. 湖南城市学院 土木工程学院，湖南 益阳，413000；

2. 上海隧道工程股份有限公司，上海，200082；

3. 长沙理工大学 交通运输学院，湖南 长沙，410075)

摘要：利用泥水盾构隧道开挖面平衡稳定原理，对泥水介质渗透的微观机理进行分析。同时，以具体工程为研究对象，结合流固耦合基本原理对由于开挖面泥水渗流所引起的隧道开挖位移场进行计算分析。研究结果表明：泥水介质向开挖面前方土体渗流时，将引起隧道地表附加沉降，且泥水压力大于主动土压力时，泥水压力越大，附加沉降量越大，但总沉降量越小；泥膜渗透系数越小、泥膜厚度越大附加沉降越小；适当增加施工进度有助于减少附加沉降。因此，在高渗透性地层条件下采用泥水盾构施工时，应确保泥水介质的质量，适当提高施工进度，尽量减少泥水渗透对开挖面稳定性及地表变形的不利影响。

关键词：泥水盾构；泥浆渗透；地表变形；流固耦合

中图分类号：TU398          文献标志码：A         文章编号：1672-7207(2013)02-0785-07

Surface deformation of slurry shield tunneling using fluid-solid coupling theory

DENG Zongwei¹, WU Zhenzhi², CAO Hao³, SHEN Pinghuan²

(1. School of Civil and Engineering, Hunan City University, Yiyang 413000, China;

2. Shanghai Tunnel Engineering Co. Ltd., Shanghai 200082, China;

3. School of Traffic and Transportation Engineering, Changsha University of Science and Technology,Changsha 410075, China)

Abstract: Based on the principle that slurry shield maintaining the stability of tunnel face, the micro mechanism of slurry infiltration was explored. The ground surface settlement due to slurry infiltration of slurry shield tunneling was analyzed using fluid-solid coupling theory. The results show that penetration of slurry into front soil in tunnel face results in additional ground surface settlement, which increases with the increase of the slurry pressure that is no less than earth pressure at rest (but the total settlement decreases with the increase of the pressure) and permeability coefficient of filter cake, decreases with thickness of filter cake. The appropriately increasing of construction schedule helps to reduce additional surface settlement. Therefore, while tunneling in highly permeable ground with slurry shield, the slurry quality should be ensured to reduce the excess water pressure. In addition, the construction schedule should also be appropriately increased to minimize the adverse effects of the slurry infiltration on the stability of tunnel face and the surface deformation.

Key words: slurry shield tunnel; slurry infiltration; surface deformation; fluid-solid coupling theory

泥水平衡盾构工法以其施工质量好、效率高、技术先进、安全可靠等优点，近年来已经得到广泛使用^[1]，使得泥水盾构隧道施工诱发的地层环境损伤问题，即地表变位的预测与控制成为亟待研究的课题^[2]。泥水平衡盾构依靠密封舱的压力泥浆来平衡开挖面水土压力来保持开挖面的稳定性及控制地表变形，泥水压力应大于地下水压力，因此泥浆介质的渗透的发生不可避免。特别当开挖面土体为粒度较大的砂土及砂砾土时，泥水将在过剩泥水压力的作用下，渗透到开挖面前方土体一定范围，导致泥水支护压力的降低和开挖面土体孔隙水压力增加及有效应力减小，从而对开挖面土体稳定性构成不利影响。鉴于以上原因，一些学者对泥浆渗透对开挖面稳定性的影响进行了分析。如Anagnostou等^[3]考虑地下水的影响，推导出隧道开挖面稳定的极限平衡条件广义表达式；Broere^[4]给出了考虑地下水影响时，隧道开挖面稳定的超孔隙水压力的经验公式；Lee等^[5]对渗流条件下的开挖面土体进行了极限平衡解析分析，分析结果与离心试验结果吻合较好；乔金丽等^[6]考虑地下水向开挖面渗流效应和不考虑水的渗流效应两种情况，对盾构隧道开挖面的稳定性进行分析；高健等^[7]考虑地下水流动引起的土体渗透变形及地下水水位变化等因素，对隧道开挖面稳定性进行了分析，采用土体极限平衡垂直条分法计算作用在隧道开挖面的有效支护压力并使用数值分析方法计算稳态地下水流条件下隧道开挖面附近的水头分布，并以广州地铁四号线隧道工程为算例进行了分析。目前研究较多是将土体向开挖面渗流而产生的渗透力作为一种定外力作用于开挖面，在此基础上研究隧道开挖面的稳定性，而针对泥水渗透对施工变形影响的研究成果尚不多见。事实上，地下水(或泥水)渗流将引起土体应力场、渗流场的改变，且渗流场和应力场之间存在耦合关系，因此仅将渗透力作为定外力来考虑显然不合理。与此同时，随着泥水盾构越来越多的应用于中心城区敏感建(构)筑物的穿越施工，针对泥水盾构施工引起的地表变形研究，尤其是基于泥浆渗透流固耦合效应的施工参数优化设置研究更具现实意义。在此，本文作者拟在揭示泥水盾构隧道开挖面泥水渗透微观机理的基础上，基于流固耦合基本原理，结合上海长江隧道长兴岛民房段推进工程，建立了可考虑泥水盾构隧道泥浆渗透流影响的地表变形流固耦合数值分析方法，据以预测了泥水支护压力、泥膜渗透系数、泥膜厚度及施工进度等主要施工参数等对地表变形的影响规律，提出了相应控制措施。该研究成果可为类似在建和待建工程提供指导和借鉴。

1  开挖面泥水渗透微观机理分析

在泥水与开挖面地层接触时，由于作用在开挖面上的泥水压力大于开挖面地层的孔隙水压力(即地下水压)，考虑到土中孔隙细小，且开挖面存在泥膜，认为泥水在土层孔隙中的流速较小，可认为是属于层流，泥水按达西定律渗入开挖面土体中，形成与土壤间隙成一定比例的悬浮颗粒，这些颗粒随泥水渗入到土体颗粒间的孔隙中，因为堵塞或交联效应，渗透到土体颗粒间隙的成一定比例的悬浮颗粒受分子间范德华力作用而被捕获，并积聚于开挖面地层与泥水的接触表面，形成泥膜。

泥水在掘削面上的渗透形态可分为3种^[8-12]，如图1所示。

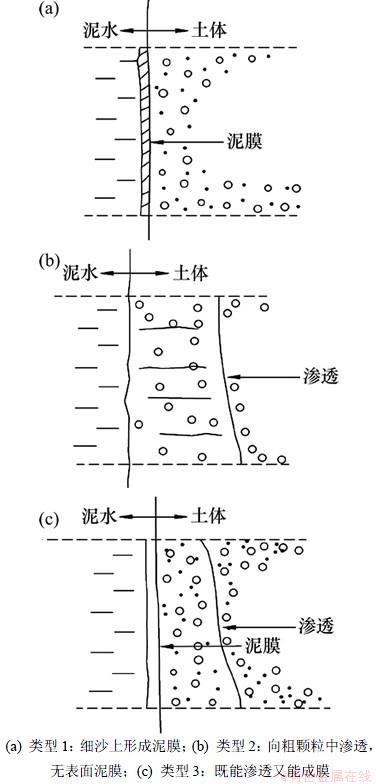
图1  泥水在掘削面上的3种渗透状态

Fig.1  Three penetration status of slurry in cutting face

类型1是地层的有效间隙 (泥水最小粒径)的情形。当泥水与掘削面开始接触后，泥水中的水渗入地层，而颗粒成分吸附聚集在掘削面表面，经过一段的时间(即成膜时间)后，掘削面上形成一层泥膜。成膜后脱水量、过剩地下水压停止增加。这种情况多发生在粘粒土、粉粒土及细砂土等土层。

类型2是地层的有效间隙 (泥水最小粒径)的情形。全部泥水可经过地层间隙流走，无法形成泥膜，渗流速度大、脱水量大、过剩地下水压大，无法稳定掘削面。这种情形多发生于粗砂、砾石等地层，其解决措施是增大泥水的粒径，即在泥水中添加砂粒。

类型3是地层有效间隙 (泥水最小粒径)的情形。泥水中的颗粒成分向地层间隙渗透、填充，最后成膜。因膜厚取决于渗透深度，所以该泥膜较类型1的吸附聚集膜厚。这种情形多发生于砂性地层(中、细)。

综上所述，类型1是泥膜在开挖面表面完全形成，即“表面泥膜”；类型2是泥水侵入过滤材料，滤层表面完全没有泥膜存在，泥水渗入滤层与滤层达到平衡，即“流变堵塞”；类型3是固体土粒子滞积在开挖面前方土体一定深度，而最终形成泥膜，泥浆水则渗入土层中，相当于“中间状态”。

“薄膜模型”，认为泥浆压力作为外力完全有效的作用于不透水的薄膜上，对应于上述的第1种渗透类型。而类型2和类型3是实际中广泛存在的情况，这2种类型都可以归结为更具代表性的“渗透模型”，即泥膜不是完全密封的，泥浆内部的水分或者泥浆本身会穿过泥膜的地层空隙，造成泥浆的损失和泥浆的失水，这种渗透作用都会减小泥浆压力的有效性，在计算中应该予以考虑。泥水渗流将引起土体应力场、渗流场的改变，且渗流场和应力场之间存在耦合关系，因此仅将渗透力作为定外力来考虑显然不合理。此外，泥浆渗透及过剩泥水压力受泥水性质、泥膜质量、泥膜厚度及盾构推进速度等因素的影响，且以上影响在渗透性较大的地层较为显著。

2  流固耦合计算原理

利用FLAC^3D 计算岩土体的流固耦合效应时，将岩体视作等效连续介质，流体在介质中的流动依据Darcy定律，同时满足Biot方程。该软件使用有限差分法进行流固耦合计算，包括以下方程^[13-14]：

(1) 平衡方程。对于小变形情况，流体质点平衡方程为

                (1)

式中：q_i为渗流速度，m/s；q_v为容积式流体源强度，s^-1；为单位体积孔隙介质的流体体积变化量。

对于饱和空隙介质，有

          (2)

式中：M为比奥模量，N/m²；p为孔隙水压力，Pa；α为比奥系数；ε为体积应变；θ为温度，℃；β为不排水温度系数(考虑流体和固体颗粒的热膨胀)，℃^-1。

动量平衡方程的形式为

             (3)

式中：ρ为体积密度，kg/m³，且ρ=(1-n)ρ_s+nρ_w，其中，ρ_s和ρ_w分别为固体和液体的密度，n为多孔介质的孔隙率，(1-n)ρ_s为基本的干密度ρ_d(ρ=ρ_d+nρ_w)；g_i(i=1，2，3)为重力加速度分量，m/s²；v_i(i=1，2，3)为介质运动速度分量，m/s。

(2) 运动方程。流体的运动用Darcy定律来描述，对于均质、各向同性固体和常密度流体的情况，达西定律的形式为

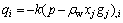           (4)

式中：k为介质的渗透系数，m²/(Pa·s)。

(3) 本构方程。体积应变的改变引起流体空隙压力的变化，反过来，空隙压力的变化也会导致体积应变的发生。空隙介质本构方程的增量形式为

      (5)

式中：△σ_ij为共旋应力增量；△p为孔隙水压力增量；△_ij为Kronecher因子；H_ij为给定函数；△ξ_ij为总应变增量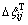；为热应变。

(4) 相容方程。应变率和速度梯度之间的关系为

             (6)

(5) 边界条件。在计算中有4种类型的渗流计算边界条件：① 给定孔隙水压力；② 给定边界外法线方向流速分量；③ 不透水边界，该边界程序中默认；④ 透水边界，透水边界采用如下形式给出：

q_n=h(p-p_e)               (7)

式中：q_n为边界外法线方向比流量分量；h为漏失系数，m³/(N·s)；p_e为渗流出口处的孔隙水压力。

3  工程实例分析

上海长江隧道是连接浦东、长兴岛的交通枢纽工程和重要的地下生命线工程，其南起浦东五好沟，北至长兴岛，共设东线和西线2条隧道，单线全长约8.9 km。隧道采用2台直径为15.43 m的超大型泥水平衡盾构施工。在长兴岛陆域段，2台超大型泥水盾构将先后穿越民房地段，这些民房均为长条形砌体结构，基础及结构刚度差，有些老民房的承重墙和横梁在盾构穿越前已出现了轻微结构损伤现象，施工涉及难度较大的环境保护问题。

隧道中心埋深15.3 m，地下水埋深2 m，穿越土层主要为②₃层灰色砂质粉土和④₁层灰色淤泥质黏土。其中，隧道中心至地表土层主要为渗透系数较大的②₃层灰色砂质粉土，因此不能忽略泥水渗透的影响。

3.1  计算模型建立

为减小边界效应影响，隧道模型的计算范围：自上取至地面，自下取至隧道底部以下3D(D为隧道直径)，横向取至隧道两侧各3D，沿轴线方向取4D。计算模型及网格划分如图2所示，网格采用8节点等参元网格，共剖分214 272个单元，223 461个节点，网络剖分见图2。土体和注浆层(等代层)单元采用Mohr-Coulomb弹塑性模型，衬砌单元采用shell单元模拟。

图2  三维网格划分模型

Fig.2  Three-dimensional model meshes

本例中隧道开挖过程的程序实现如图3所示。首先去除需开挖管片环的地层单元，同时添加管片单元来模拟该环管片的支护，在开挖面上施加泥水支护应力，关闭FLAC3D中的流体渗流分析部分，计算模型在单力学场中的土体不排水变形量，迭代计算使模型在不排水状态下达到平衡，然后开启流体渗流场，使用流固耦合计算土体在该环开挖时间内的排水变形量(固结变形量)，耦合计算该时步完成后，进入下一环开挖过程计算，如此往复循环，直至隧道完成后进入下一环开挖过程计算，如此往复循环，直至隧道完成。

图3  FLAC3D处理盾构开挖循环流程

Fig.3  Cycling process for solve fluid-solid coupling problem shield using excavation FLAC3D

3.1.1  地层参数

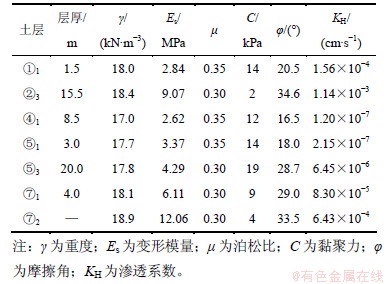
土体物理力学参数如表1所示，其中C和φ采用有效应力强度抗剪指标。

表1  土体物理力学参数

Table 1  Physico-mechanical parameters of soils

3.1.2  管片与盾尾空隙参数

衬砌弹性模量取37.4 MPa(考虑管片接头影响，根据接头试验结果，对衬砌整体刚度折减系数取为0.80)，泊松比取0.167。采用“等代层”来描述盾构施工过程中盾尾空隙的大小、注浆充填密实程度、隧道周围土体的扰动程度与范围，根据施工实测位移反分析结果，取等代层性质参数为：E=40 MPa，μ=0.30，γ=20 kN/m³。

3.1.3  泥水参数

泥水重度取12 kN/m³，泥膜力学指标参考土层参数作相应提高：压缩模量E_s=20 MPa，μ=0.30，C=30 kPa，φ=30°。

经计算，切口水压上限值(静止土压力)和下限值(主动土压力)分别为268 kPa和223 kPa，因此，本次计算选用了270，250和230 kPa 3种泥水压力情况。

泥膜渗透系数K取3种情况：1×10^-7 cm/s，1×10^-5 cm/s及清水情况(泥舱中泥水为清水，相应厚度泥膜物理力学参数按原状土选取)。

3.2  计算结果及分析

正常情况下，隧道1环的施工时间(包括盾构推进、管片拼装及泥浆管接长)为2 h左右，如遇机械故障或其他情况，隧道1环施工时间将加长。这里施工进度取3种情况，即2 h/环、4 h/环和6 h/环。这里取开挖至第4环时的计算结果进行分析，不考虑及考虑流固耦合2种情况下，隧道开挖后地表变形进行对比，并定量分析泥水压力、泥膜厚度、泥膜渗透系数、施工进度等因素的影响规律。

3.2.1  泥水压力的影响

图4所示为地表横向沉降对比曲线。其中耦合情况取泥膜厚度10 mm，泥膜渗透系数1.0×10^-7 cm/s，施工进度2 h/环。

图4  地表横向沉降槽曲线

Fig.4  Relationship between slurry pressure and ground transverse settlement

由图4可见：考虑流固耦合作用时的地表沉降计算值均大于不考虑流固耦合情况，由于泥浆渗透引起的横向附加沉降为3.0~5.5 mm，且地表沉降值随着支护压力的减少而增大。

3.2.2  泥膜渗透系数的影响

图5所示为泥膜厚度为10 mm，施工进度为2 h/环，泥膜为不同渗透系数时隧道的水平地表沉降曲线。

图5  地表横向沉降与泥膜渗透系数的关系曲线

Fig.5  Relationship between permeability coefficient of filter cake and ground transverse settlement

由图5可见：随着泥膜渗透系数的增大，隧道地表沉降也不断增大，当泥膜渗透系数为1×10^-7 cm/s，1×10^-5 cm/s及泥水舱加清水时，由泥浆渗透导致的最大地表附加沉降分别为3.5，11.3和27.0 mm。

3.2.3  泥膜厚度的影响

图6所示为施工进度为2 h/环，泥膜渗透系数取1×10^-7cm/s，泥膜取不同厚度时的隧道的地表沉降曲线。

由图6可见：随着泥膜厚度的增大，隧道地表沉降值也不断减小，当泥膜厚度分别为15，10和5 mm时，由于泥浆渗透导致的最大附加沉降为1.3，3.5及26.2 mm。

3.2.4  施工速率的影响

图7所示为泥膜厚度10 mm，泥膜渗透系数取1×10^-7cm/s，不同施工进度时的隧道的水平地表沉降曲线。

由图7可见：随着施工进度的加快，隧道地表沉降值也不断减小，当施工进度分别为2，4和6h/环时，由于泥浆渗透导致的最大附加沉降为3.5，18.4及37.1 mm。

图6  地表横向沉降与泥膜厚度的关系曲线

Fig.6  Relationship between thickness of filter cake and ground transverse settlement

图7  地表横向沉降与施工进度的关系曲线

Fig.7  Relationship between construction schedule and ground transverse settlement

4  实际施工措施

根据以上计算分析结果，针对上海长江隧道民房段施工采取了以下措施：

(1) 考虑到泥浆渗透影响，切口水压按略大于静止土压力选取，本次施工中切口水压保持在270 kPa左右。

(2) 采用法国进口的“MS”高效、可靠泥水处理系统，同时定期对泥水指标进行检查，泥水指标控制为： 相对密度ρ=1.15~1.20；黏度ν＞25 s；析水率＜5%，确保了泥膜生成质量。

(3) 在穿越民房段前，对相关设备进行了检修，以避免穿越民房段期间因设备故障而导致盾构长时间停机。适当提高了民房段盾构推进速度，推进速率为40~45 mm/min，施工进度为2 h/环左右。通过优化工序衔接，盾构快速通过了民房地段。

由于采取了以上合理措施，将最大地表沉降控制在25 mm以下，地层损失率控制在3‰左右，监测结果和上述预测计算结果吻合较好，避免了盾构施工对穿越民房的不良影响。

5  结论

(1) 揭示了泥水盾构隧道开挖面泥水渗透微观机理，基于流固耦合基本原理，结合上海长江隧道长兴岛砂性土地层民房穿越工程，采用FLAC3D 软件，针对泥水渗流相关因素对泥水盾构隧道施工地表变形的影响规律进行了定量计算分析，并据以对民房段施工进行了指导。

(2) 泥水向开挖面前方土体渗流时，将引起开挖面前方超孔隙水压力的增加和开挖面有效支护压力的减少，从而导致隧道地表附加沉降，且这种影响与泥水压力、泥膜渗透系数、泥膜厚度及施工进度等施工参数有关。泥水压力大于主动土压力时，泥水压力越大，附加沉降量越大，但总沉降量越小；泥膜渗透系数越小、泥膜厚度越大附加沉降越小；适当增加施工进度有助于减少附加沉降。

(3) 在高渗透性地层条件下，采用泥水盾构施工时，应确保泥水的质量(施工前可开展黏性、可渗比、脱水量测定)，以减少过剩地下水压力，同时应合理设定切口泥水压力(考虑过剩泥水压力对有效支护压力的影响)，适当增加施工进度(周围环境复杂情况下应避免长时间停机)，尽量减少泥水渗透对开挖面稳定性及地表变形的不利影响。

参考文献：

[1] 程展林, 吴忠明, 徐言勇. 砂基中泥浆盾构法隧道施工开挖面稳定性试验研究[J]. 长江科学院院报, 2001, 18(5): 53-55.

CHEN Zhanlin, WU Zhongming, XU Yanyong. Experimental study on stability of tunnel excavation surface in sand foundation by slurry shield method[J]. Journal of Yangtze River Scientific Research Institute, 2001, 18(5): 53-55.

[2] 韦良文, 张庆贺, 邓忠义. 大型泥水盾构隧道开挖面稳定机理与应用研究[J]. 地下空间与工程学报, 2007, 3(1): 87-91.

WEI Liangwen, ZHANG Qinghe, DENG Zhongyi. Research on mechanism and application of face stability in large slurry shield tunneling[J]. Chinese Journal of Underground Space and Engineering, 2007, 3(1): 87-91.

[3] Anagnostou G, Kovari K. Face stability conditions with earth-pressure-balanced shields[J]. Tunnels and Underground Space Technology, 1996, 11(2): 165-173.

[4] Broere W. Face stability calculation for a slurry shield in Heterogeneous soft soils[J]. Tunnels and Metropolises, 1998, 23: 215-218.

[5] Lee I M, Nam S W, Jae H A. Effect of seepage force on tunnel face stability[J]. Canadian Geotechnical Journal, 2003, 40(2): 342-350.

[6] 乔金丽, 张义同, 许春彦. 考虑渗流的盾构隧道开挖面稳定性分析[J]. 水文地质与工程地质, 2009(1): 80-85.

QIAO Jinli, ZHANG Yitong, XU Chunyan. Stability analysis of shield tunnel excavation face with the consideration of seepage[J]. Hydrogeology & Engineering Geology, 2009(1): 80-85.

[7] 高健, 张义同, 乔金丽. 渗透力对隧道开挖面稳定性影响分析[J]. 岩土工程学报, 2009, 31(10): 1547-1553.

GAO Jian, ZHANG Yitong, QIAO Jinli. Face stability analysis of tunnels with consideration of seepage force[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(10): 1547-1553.

[8] 韩晓瑞, 朱伟, 刘泉维, 等. 泥浆性质对泥水盾构开挖面泥膜形成质量影响[J]. 岩土力学, 2008, 29(增刊): 288-292.

HAN Xiaorui, ZHU Wei, LIU Quanwei, et al. Influence of slurry property on filter-cake quality on working face of slurry shield[J]. Rock and Soil Mechanics, 2008, 29(Suppl): 288-292.

[9] 张凤祥, 朱合华, 傅德明. 盾构隧道[M]. 北京: 人民交通出版社, 2004: 183-184.

ZHANG Fengxiang, ZHU Hehua, FU Deming, et al. Shield tunnel[Μ]. Beijing: People’s Communication Press, 2004: 183-184.

[10] Fritz P. Additives for slurry shields in highly permeable ground[J]. Rock Mechanics and Rock Engineering, 2007, 40(1): 81-95.

[11] 白云, 孔祥鹏, 廖少明. 泥水盾构泥膜动态形成机制研究[J]. 岩土力学, 2010, 31(增刊2): 19-24.

BAI Yun, KONG Xiangpeng, LIAO Shaoming. Research on dynamic formation mechanism of slurry membrane for slurry shield[J]. Rock and Soil Mechanics, 2010, 31(Suppl 2): 19-24.

[12] 王胜勇, 吕建中, 刘钧钧. 泥膜性能对大口径隧道开挖面稳定性影响[J]. 工业建筑, 2010, 40(增刊): 629-631.

WANG Shengyong, L Jianzhong, LIU Junjun. Influence of performances of filter cake on the stability of excavation surface in heavy calibre tunnel[J]. Industrial Construction, 2010, 40(Suppl): 629-631.

[13] Itasca Consulting Group Inc. FLAC3D fluid-mechanical interaction (Version 2.1)[M]. Itasca: Itasca Consulting Group Inc, 2003: 2-6.

[14] 李地元, 李夕兵, 张伟, 等. 基于流固耦合理论的连拱隧道围岩稳定性分析[J]. 岩石力学与工程学报, 2007, 26(5): 1056-1064.

LI Diyuan, LI Xibing, ZHANG Wei, et al. Stability analysis of surrounding rock of multi-arch tunnel based on coupled fluid-solid theorem[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 1056-1064.

(编辑  杨幼平)

收稿日期：2012-04-23；修回日期：2012-06-12

基金项目：湖南省教育厅重点研究项目(09A016)；上海市博士后基金重点资助项目(08R214210)

通信作者：邓宗伟(1972-)，男，湖南益阳人，博士后，副教授，从事岩土工程与隧道工程研究；电话：13973760738；E-mail：teapotd@163.com