Effect of ambient wind on pressure wave generated by high-speed train entering a tunnel
来源期刊:中南大学学报(英文版)2017年第6期
论文作者:刘堂红 周细赛 陈争卫 邹翔 刘东润
文章页码:1465 - 1475
Key words:high-speed train; ambient wind; pressure wave; tunnel
Abstract: Using three-dimensional, unsteady N-S equations and k-ε turbulence model, the effect of ambient wind on the pressure wave generated by a high-speed train entering a tunnel was studied via numerical simulation. Pressure changes of the train surface and tunnel wall were obtained as well as the flow field around the train. Results show that when the train runs downwind, the pressure change is smaller than that generated when there is no wind. When the train runs upwind, the pressure change is larger. The pressure change is more sensitive in the upwind condition than in the downwind condition. Compared with no wind condition, when the wind velocity is 10 m/s and 30 m/s, the pressure amplitude on the train head is reduced by 2.8% and 10.5%, respectively. The wall pressure amplitude at 400 m away from the tunnel entrance is reduced by 2.4% and 13.5%, respectively. When the wind velocity is -10 m/s and -30 m/s, the pressure amplitude on the train head increases by 3.0% and 17.7%, respectively. The wall pressure amplitude at 400 m away from the tunnel entrance increases by 3.6% and 18.6%, respectively. The pressure waveform slightly changes under ambient wind due to the influence of ambient wind on the pressure wave propagation speed.
Cite this article as: ZHOU Xi-sai, LIU Tang-hong, CHEN Zheng-wei, ZOU Xiang, LIU Dong-run. Effect of ambient wind on pressure wave generated by high-speed train entering a tunnel [J]. Journal of Central South University, 2017, 24(6): 1465-1475. DOI: 10.1007/s11771-017-3550-5.
J. Cent. South Univ. (2017) 24: 1465-1475
DOI: 10.1007/s11771-017-3550-5
ZHOU Xi-sai(周细赛)1, 2, LIU Tang-hong(刘堂红)1, 2, CHEN Zheng-wei(陈争卫)1, 2,
ZOU Xiang(邹翔)1, 2, LIU Dong-run(刘东润)1, 2
1. Key Laboratory of Traffic Safety on Track of Ministry of Education, Central South University,Changsha 410075, China;
2. School of Traffic & Transportation Engineering, Central South University, Changsha 410075, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract: Using three-dimensional, unsteady N-S equations and k-ε turbulence model, the effect of ambient wind on the pressure wave generated by a high-speed train entering a tunnel was studied via numerical simulation. Pressure changes of the train surface and tunnel wall were obtained as well as the flow field around the train. Results show that when the train runs downwind, the pressure change is smaller than that generated when there is no wind. When the train runs upwind, the pressure change is larger. The pressure change is more sensitive in the upwind condition than in the downwind condition. Compared with no wind condition, when the wind velocity is 10 m/s and 30 m/s, the pressure amplitude on the train head is reduced by 2.8% and 10.5%, respectively. The wall pressure amplitude at 400 m away from the tunnel entrance is reduced by 2.4% and 13.5%, respectively. When the wind velocity is -10 m/s and -30 m/s, the pressure amplitude on the train head increases by 3.0% and 17.7%, respectively. The wall pressure amplitude at 400 m away from the tunnel entrance increases by 3.6% and 18.6%, respectively. The pressure waveform slightly changes under ambient wind due to the influence of ambient wind on the pressure wave propagation speed.
Key words: high-speed train; ambient wind; pressure wave; tunnel
1 Introduction
When a train suddenly enters a tunnel from open air, it can cause severe transient pressure changes on the train surface and the tunnel wall, which worsens the train operation safety and passenger comfort [1-3]. During the process of train entering a tunnel, the air initially inside the tunnel is strongly compressed by a piston effect in the train head neighborhood and gives rise to a compression wave that propagates at the sound speed in the tunnel. Some part of the compression wave is reflected back from the tunnel exit as an expansion wave and a part of it emerges as a pressure pulse, called micro-pressure wave. The micro-pressure wave creates a booming noise that causes residents near the trackside to suffer from noise pollution [4-6]. Therefore, much research was performed to analyse pressure waves that are generated by trains entering tunnels to increase transportation efficiency.
MOK and YOO [7] studied four types of tunnel entrance shapes to investigate the formation of a compression wavefront at the tunnel entrance via the finite element method using the Euler equation. The results show the possibility of a partial change in the compression wavefront using an optimal combination of the degree of tunnel entrance slopes and holes in the tunnel entrance ceiling. FUKUDA et al [8] performed field measurement and numerical simulation on the distortion of compression wave that was generated by a train entering a tunnel. The results indicate that the compression wavefront steepens in the early stage and become smoother in the later stage of propagation. SHIN and PARK [9] used a three-dimensional, compressible, unsteady N-S equation to simulate aerodynamics changes and pressure waves generated by a train running through a tunnel. To account for the relative motion of stationary tunnel and the moving train, they have implemented the sliding multi-block method. LIU and TIAN [10] performed experiments to study the micro-pressure wave and airflow caused by trains entering tunnels. Their results show that 43% of the surveyed people have obvious discomfort when the train passes through the tunnel at 200 km/s, and the airflow velocity caused by the train exceeds the human security level, which is 14 m/s. UYSTEPRUYST et al [11] presented a new methodology based on the solutions of Euler equations for the numerical simulation of high- speed trains entering a tunnel. They developed non- reflecting boundary conditions for non-structured three- dimensional meshes to limit the calculation domain. RABANI and FAGHZH [12] simulated the turbulent flows generated by the moving train in a tunnel using the remeshing method and the RNG k-ε turbulence model. Their results show that the air vents and enlarged hood at the portal attenuate the pressure gradient and drag coefficient by approximately 28% and 36%, respectively. KIKUCHI et al [13] studied the optimal longitudinal distribution of cross-sectional area of the train nose shape for suppressing the micro-pressure wave using the rapid computational scheme and a genetic algorithm.
During the period from June 2014 to May 2015, many full-scale tests were performed to investigate aerodynamic performance of high-speed trains running in windy areas and the aerodynamic effects caused by trains entering tunnels for the successful launch of the Lanzhou-Xinjiang high-speed railway. According to the requirements and test procedures for aerodynamics in tunnels [14], ideally there should be no initial airflow in the tunnel for the full scale measurement of pressure changes. However, if there is, its influence on the measurements should be determined. Xinjiang railway is in the windy area, and the number of days with level 8 winds exceeds 200. Thus, there is either a weak or strong wind during the tests. Therefore, the tests for aerodynamic effects caused by trains entering tunnels must be performed taking into consideration the influence of ambient wind. When full-scale tests are performed in windy areas, it is found that there will be a greater wind speed along the line when the ambient air is affected by the terrain and wind-break wall, which will result in a larger airflow in the tunnel. The train will be impacted by the combined effects of initial airflow and train-induced airflow. Thus, the flow field around the train will be more complex, and the aerodynamic effects caused by the train entering a tunnel will also be changed due to the space constraints of the tunnel and the train motion. To accurately evaluate aerodynamic effects caused by a train entering a tunnel under ambient wind, it is necessary to consider the effect of ambient wind on pressure waves in the tunnel using relevant numerical simulation and field test data. It can be seen that previous researches did not consider the effect of ambient wind in the tunnel. Therefore, the aim of the present study is to investigate pressure variation on the train surface and tunnel wall, which is induced by a train travelling through the tunnel under ambient wind using the sliding mesh method. Simulation results were analyzed to understand the influence of ambient wind on pressure waves in the tunnel.
2 Numerical simulation model
2.1 Mathematical model
A compressible, unsteady, turbulent flow simulation is used to investigate the aerodynamic effect caused by a high-speed train entering and running through the tunnel under ambient wind. The standard k-ε turbulence model is used. The governing equations are the continuity equation and the Reynolds-averaged Navier-Stokes equations [15].
Continuity equation:
 (1)
(1)
Momentum equation:
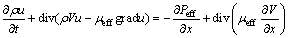 (2)
(2)
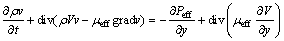 (3)
(3)
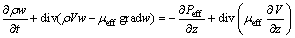 (4)
(4)
k equation:
 (5)
(5)
ε equation:
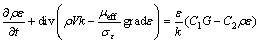 (6)
(6)
where ρ is the air density; V is the velocity vector; u, v and w are the velocity components in the x, y and z directions, respectively; k is the turbulent kinetic energy; ε is the kinetic energy dissipation rate of the turbulence; G is the turbulence production rate; μeff and Peff are the effective dynamic viscosity and effective pressure, respectively; C1, C2, σk and σε are the experimentally determined constants, C1=1.44, C2=1.92, σk=1.0, σε=1.33.
The abovementioned governing equations were solved using the commercial code Fluent 6.3. The SIMPLEC algorithm was applied to solve the pressure-velocity coupling, with second order upwind momentum and time discretization scheme. To obtain a stable initial flow field, first, the train was kept stationary and ambient wind was applied to the tunnel. Then, the train motion was induced after the initial flow field was fully developed in the tunnel. The train speed was 250 km/h, which was M=0.2 in terms of a Mach number. The sliding mesh method was used to implement the train motion relative to the tunnel. The time step was 0.006 s, which was sufficiently small to resolve the unsteadiness in the flow field.
2.2 Computational grid and boundary conditions
The train model was based on the Chinese high- speed train CRH2. To more realistically simulate the transient pressure changes that are generated by a train entering a tunnel, the train consisting of a head car, 6 middle cars and a tail car was used in this work. The total length was 201.4 m and the train did not include handles and pantographs, but bogies and windshields were included. The cross-sectional area of the train was 11.29 m2. Because the train geometry was complicated, a more adaptive non-structured grid method was used for discretization, as shown in Fig. 1. The tunnel model depended on the Number 1 Tunnel of Xinjiang 13 Rooms, which was a double-tracked tunnel with a length of 1222 m. The gap (lateral distance) between track centres was 5 m. Figure 2 shows the cross-section of the tunnel. The cross-sectional area of the tunnel was 100 m2, and the blockage ratio was 11.29%.
The computational domain was composed of the tunnel, tunnel entrance and tunnel exit. The tunnel entrance and exit surroundings were dimensioned so that the external domain boundaries do not affect the flow close to the tunnel portal, as shown in Fig. 3. The external domain was 600 m in length, 120 m in width and 60 m in height. The initial distance of the train from the tunnel was 50 m to ensure the stability of numerical simulation. The no-slip solid-wall boundary condition was used for the train body, the tunnel wall and the ground. The far-field boundary condition was used for the external domain.

Fig. 1 Surface mesh of head car
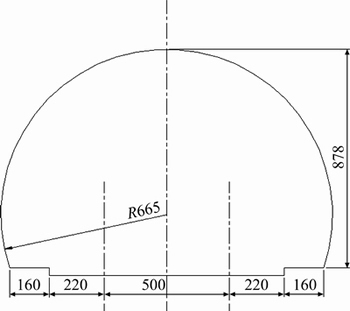
Fig. 2 Cross-section of tunnel (Unit: cm)
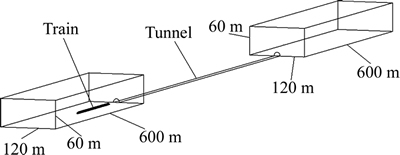
Fig. 3 Computational domain and boundary conditions
Figure 4 shows the applying method of ambient wind in the tunnel. When the computation began, the train speed was set at 250 km/h. Ambient wind of 10, 20 and 30 m/s was applied to the tunnel entrance, and the directions of wind speed and train speed were the same. When the train travelled in the opposite direction to the ambient wind, the wind of -10, -20 and -30 m/s was applied to the tunnel exit, and the negative sign represented the direction, which was opposite to the train speed. The corresponding wind velocity was 0 without an ambient wind in the tunnel.
2.3 Arrangement of measuring points
Many measuring points were set on the train surface to analyze the transient pressure changes. Point arrangements on the head and tail cars were the same, and each car had 15 points. Each middle car had 10 measuring points at the same locations on the train surface, as shown in Fig. 5. In total, 11 measuring points were located on the tunnel wall at a height of 4.2 m from the ground to investigate the effect of ambient wind on pressure changes in the tunnel, which is shown in Fig. 6.

Fig. 4 Applying method of ambient wind in tunnel
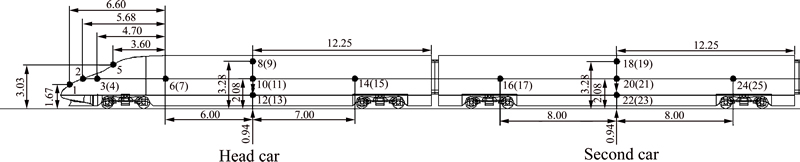
Fig. 5 Point arrangements of high-speed train model (Unit: m)
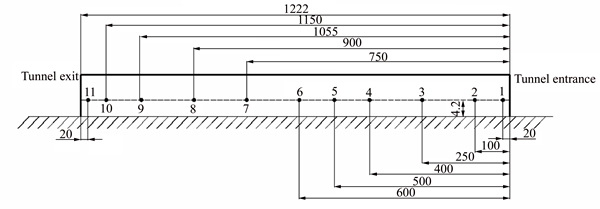
Fig. 6 Point arrangements of tunnel model (Unit: m)
3 Model verification
In November 2014, Urumqi Railway Bureau organized the Central South University and the China Academy of Railway Sciences to perform full-scale tests of CRH2 running along the Lanzhou-Xinjiang railway in the Baili wind areas. To verify the calculation method used in the paper, the present model was applied to simulate the field observation of the full-scale test. The aerodynamic pressure that was generated by a train entering the Number 1 Tunnel of Xinjiang 13 Rooms at a speed of 180 km/h under the wind of 8.2 m/s along the line was measured. The pressure of the measuring point 10 on the head car surface attained from the simulation was compared to the experimental data, as shown in Table 1. Pmax means the maximum pressure, Pmin means the minimum pressure, △P represents the pressure amplitude, and △P=Pmax-Pmin. Figure 7 portrays the pressure variation time history of measuring point 10 on the head car surface.
The present pressure variation was in good agreement with the experimental result. The pressure amplitude was slightly different, and the deviation was less than 5%. This indicates that the numerical calculation method was suitable to be applied to the study on aerodynamic effect caused by a train entering a tunnel. After t>19 s, the difference of pressure was greater due to the change of train speed in the tunnel during the test.
Table 1 Result comparison of numerical computation and full- scale test
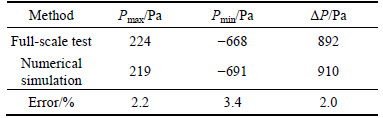
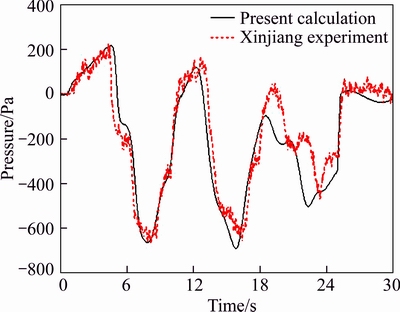
Fig. 7 Time history of pressure at measuring point 10 on head car
4 Numerical simulation results and analysis
4.1 Analysis of pressure variation on tunnel wall
Figure 8 presents pressure amplitude △P of measuring points on the tunnel wall at different locations under different wind velocities. The pressure amplitudes of different measuring points are different at the same wind velocity, which is the maximum for measuring point 4 and the minimum for measuring point 11. When the wind velocity is 0 m/s, the pressure amplitudes of measuring points 4 and 11 are 2858 Pa and 1270 Pa, respectively, and the difference is 55.56%. Additionally, the pressure amplitude of the same measuring point varies under different wind velocities, compared with the measurements without wind. Specifically, the pressure amplitude is reduced when the train travels downwind, and the greater the wind speed, the smaller the pressure amplitude. When the train runs against the wind, the pressure amplitude is increased, and it increases with the wind speed. Table 2 shows the change rate of the pressure amplitude on tunnel wall at different wind velocities compared with measurements without wind. The positive numbers indicate the increased proportion of pressure amplitude and the negative numbers represent the reduced proportion of pressure amplitude, compared with results measured at wind velocity of 0 m/s.
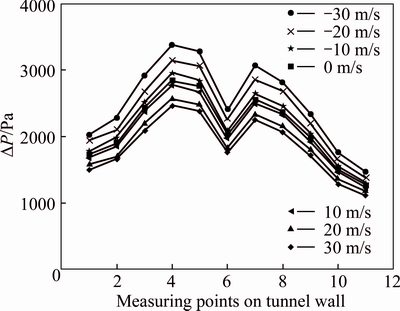
Fig. 8 Pressure amplitude on tunnel wall under different wind velocities
As seen in Table 2, the ambient wind has less impact on the pressure amplitude when the wind velocity is 10 m/s. The most significant change is observed at the measuring point 11, which decreases by 3.6%, while only by 1.4% for the measuring point 1. When the wind
velocity is -30 m/s, the change rates of pressure amplitudes of all measuring points are more than 16%, and the pressure amplitude of the measuring point 2 changes significantly, which increases by 20.4%. When the wind velocity is 30 m/s, the most obvious change occurs at the measuring point 10, specifically, the pressure amplitude decreases only by 14.4%. Thus, the pressure amplitude change is more sensitive under the upwind condition than under the downwind condition.
Figure 9 shows time variations of wall pressure induced by the train passing through the tunnel under ambient wind (for measuring point 4 and 10). As seen in Fig. 9, pressure waveforms vary due to different locations on the wall, but the change laws are identical. The pressure of measuring point increases when it meets a compression wave, and drops due to an expansion wave. The pressure rapidly decreases when the train nose passes the measuring point. Then, the passing of the train tail sharply increases the pressure [16]. Furthermore, there is a continuous pressure fluctuation when the train body passes through the measuring point due to the inter-carriage gaps. The pressure of measuring points changes at different wind velocities. Compared with the no wind condition, the maximum and minimum pressures increase when the wind velocity is -30 m/s. The maximum pressures of measuring points 4 and 10 increase by 22.0% and 22.5%, respectively. Additionally, the minimum pressures of measuring point 4 and 10 increase by 16.3% and 13.9%, respectively. However, the maximum and minimum pressures are reduced when the wind velocity is 30 m/s. The maximum pressure decreases by 10.4% for the measuring point 4, and by 11.7% for the measuring point 10. Furthermore, the minimum pressures of measuring points 4 and 10 reduce by 15.7% and 16.3%, respectively. The results reveal that the ambient wind has a significant effect on the strength of pressure waves.
The initial compression waves of measuring points 4 and 10 are shown in Fig. 10. As seen in Fig. 10, the initial compression waveforms of measuring points 4 and 10 are different, owing to the location of the measuring point in the tunnel. The initial compression waveform also changes under different wind velocities. Furthermore, the difference of waveforms is more obvious farther away from the tunnel entrance. The time required for the pressure to increase from zero to the maximum positive peak is different for different velocities. Compared with the condition without wind, the time lags when the wind velocity is -30 m/s, and the time advances when the wind velocity is 30 m/s. This occurs because ambient wind influences the propagation of sound wave. Specifically, the downwind wind field makes the sound wave propagate faster, and it propagates slower in the case of the upwind wind field [17]. However, low-speed wind (30 m/s) has little effect on the propagation of sound wave, as shown in Fig. 10(a), and the time required for the pressure to increase from zero up to the maximum positive peak is approximately the same at different wind velocities. However, when the propagation distance of pressure wave increases, the time difference accumulates and becomes apparent, as shown in Fig. 10(b). The time is reduced by 0.06 s when the wind velocity is 30 m/s and increases by 0.072 s when the wind velocity is -30 m/s, compared with measurements without wind. Thus, ambient wind changes the pressure wave strength and waveform.
Table 2 Change rate of pressure amplitude of different measuring points under different wind velocities compared with measurements without wind

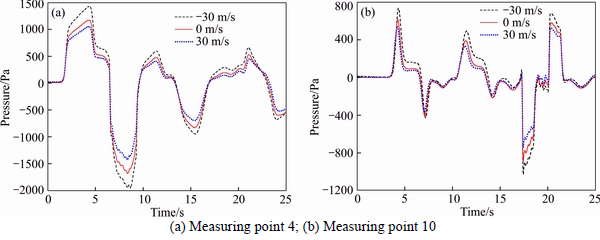
Fig. 9 Time history of wall pressures under different wind velocities:
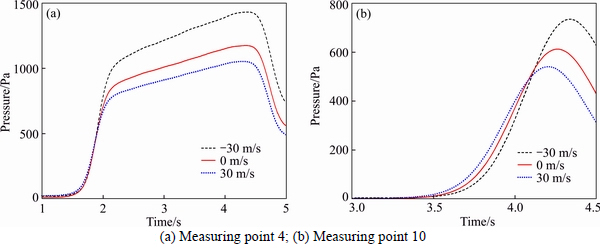
Fig. 10 Time history of initial compression waves under different wind velocities:
Part of the initial compression wave is discharged to the atmosphere as a pulse-like wave. Thus, a micro- pressure wave is formed. The micro-pressure wave strength is proportional to the maximum value of pressure gradient of the initial compression wave.Figure 11 presents the relationship between the maximum pressure gradient and wind velocity. It can be seen in Fig. 10 that the relationship between them is linear, and the correlation coefficient R2=0.957. Compared to the no wind condition, the difference is only 1.7% when the wind velocity is 10 m/s, which becomes obvious when the wind speed reaches 30 m/s. When the wind velocity is -30 m/s, the maximum pressure gradient is increased by 18.2%, and it is reduced by 11.7% when the wind velocity is 30 m/s.
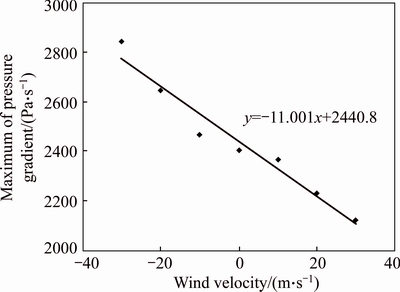
Fig. 11 Relationship between maximum pressure gradient and wind velocity
4.2 Analysis of pressure variation on train surface
When the high-speed train enters the tunnel, the air in front of the train head is compressed due to compressibility and limited space in the tunnel. Thus, the air pressure rises. As the train further enters the tunnel, the pressure of the train surface gradually increases until the train tail gets into the entrance. Time variations of the train surface pressure of different measuring points without ambient wind are presented in Fig. 12.
In Fig. 12(a), the pressures of measuring points on the train head are significantly different because of large changes of the streamlined head curvature. The maximum positive pressure of the measuring point 1, which is close to the train nose, is 1568 Pa. This value is larger than the pressure of other measuring points. However, the maximum negative pressure is the smallest and is approximately -333 Pa. The difference in pressure amplitude among five measuring points is not significant and is less than 2%. As seen in Fig. 12(b), the pressure curves of measuring points at different longitudinal locations on the same side of train body are coincident due to a relatively simple geometry of the middle part of the train. Additionally, pressure waves and amplitudes of the measuring points at different vertical heights are consistent, as shown in Fig. 12(c). From the abovementioned analysis, the pressures of the measuring point 1 near the train nose and the measuring point 20 on the middle part of the second car are selected to study the effect of ambient wind on the train aerodynamic performance.
Figure 13 shows pressure variations of the measuring points 1 and 20 under different wind velocities. In Fig. 13(a), the pressure of measuring point 1 rises rapidly when the train nose enters the tunnel. The maximum pressure changes from 1922 Pa to 1403 Pa with a difference of 27% when the wind velocity changes from -30 m/s to 30 m/s. When t=8.7 s, the minimum pressure of measuring point 1 is observed due to the expansion wave, but the values have little difference under different wind velocities. In Fig. 13(b), the maximum pressures of measuring point 20 are less than 500 Pa without a significant difference under ambient wind. However, there is a significant difference among the minimum pressures due to the expansion wave. The wind velocity varies from -30 m/s to 30 m/s, and the minimum pressure changes from -1807 Pa to -1325 Pa with a difference of 26.7%. Additionally, it is found that the time when pressure peaks and valleys occur slightly changes under different wind velocities as pressure waves constantly reflect back and forth. This occurs because the propagation speed of pressure waves changes in the ambient wind field.
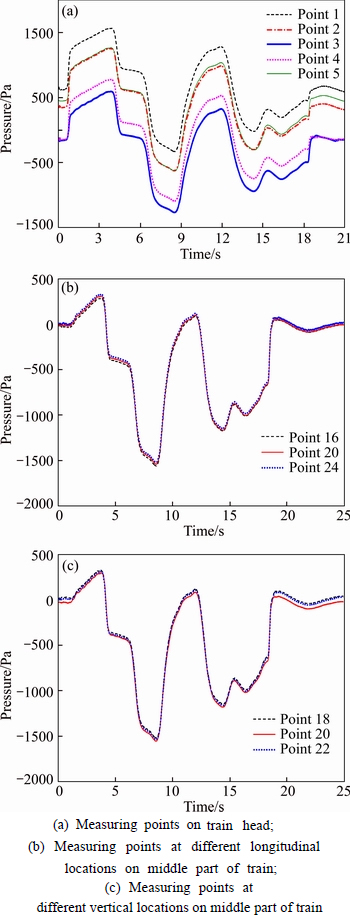
Fig. 12 Time history of train surface pressures at different locations under no wind condition:
Figure 14 portrays the maximum (Pmax) and minimum (Pmin) pressures as well as the pressure amplitude (△P) of measuring points 1 and 20 under different wind velocities. It is found that the pressure amplitude of measuring point 1 significantly varies due to the maximum pressure difference. However, the change of pressure amplitude of measuring point 20 results from the minimum pressure variation. When the wind speed is 10 m/s, ambient wind has a slight influence on the pressure of the train surface, which is changed only by approximately 3% compared with the no wind condition. The influence of ambient wind on the aerodynamic effect becomes more significant with the wind speed increase. When the wind velocity is 30 m/s, the pressure amplitude of the measuring point 1 decreases by 10.5%, and the pressure amplitude of the measuring point 20 is reduced by 13.0%. When the wind velocity is -30 m/s, the pressure amplitude increases by 17.7% and 17.3% for the measuring points 1 and 20, respectively. Thus, aerodynamic effects can be alleviated when the train enters the tunnel downwind. However, aerodynamic effects will deteriorate if the train runs against the wind in the tunnel.

Fig. 13 Time history of train surface pressures under different wind velocities:

Fig. 14 Pressure variations on train surface under different wind velocities:
4.3 Flow field analysis around train
To further understand the effect of ambient wind on pressure distribution on the train, three different wind velocities of 30 m/s, 0 m/s and -30 m/s are analyzed in this section. Figures 15 and 16 depict pressure contours around the train at t=3.6 s and t=8.7 s, respectively. In Fig. 15, the pressure around the train head is positive when the entire train enters the tunnel completely at t=3.6 s. When the wind velocity is 30 m/s, the pressure around the train nose significantly decreases compared with the wind velocity of 0 m/s. Furthermore, the train body surface is under a small positive pressure area, which decreases slightly. However, when the wind velocity is -30 m/s, the air pressure near the train nose noticeably increases, and the pressure on the train body surface rises within a small range. Therefore, the maximum pressure of the measuring point 1 is more sensitive to the wind velocity than that of the measuring point 20. As seen in Fig. 16, at t=8.7 s, the pressure on the train surface becomes negative due to the influence of expansion wave except for the nose area and the front window portion. The pressure on the train body surface including measuring point 20 significantly decreases when the wind velocity varies from 30 m/s to -30 m/s. This indicates a greater strength of the expansion wave,which is generated by the train travelling upwind. When the train travels upwind, the air in front of the train head is compressed more significantly, which increases the pressure. However, the stronger expansion wave decreases the pressure around the nose area. Therefore, there is no significant difference in the minimum pressure of the measuring point 1 with the wind velocity change.

Fig. 15 Pressure contours around train at t=3.6 s under different wind velocities:
Figures 17 and 18 present the streamlines around the train head and train tail, respectively, under different wind velocities at t=3.6 s. As shown in Fig. 17, when the train travels in the tunnel without wind, one part of air parted by the train flows forward along the tunnel and another part flows backward through the annular space between the tunnel wall and the train surface. When the train runs downwind, most of the air around the train head area flows forward, which weakens the compression of air. Thus, the strength of the compression wave is also reduced. When the train travels against the wind, the air in front of the train head mostly flows backward through the annular space, and the air compression is strengthened, which results in an increased strength of the compression wave. Once the train tail enters the tunnel, the expansion wave is formed. This occurs because the amount of air flowing behind the train tail is less than the amount of air being parted by the train. This results in pressure difference between the atmosphere and the tunnel entrance. As shown in Fig. 18, it is helpful for the air to flow into the tunnel entrance when the train runs in the same direction with the wind velocity. Then, the pressure difference becomes smaller, and the expansion wave strength is reduced. When the train enters the tunnel against the wind, more air is parted out of the tunnel. Thus, the pressure difference becomes larger, which increases the strength of expansion wave. These flow field characteristics explain the influence of ambient wind on transient pressure changes of the tunnel wall and the train surface.
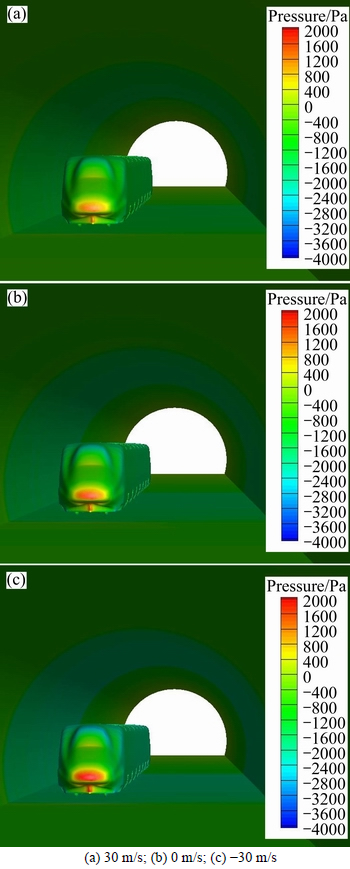
Fig. 16 Pressure contours around train at t=8.7 s under different wind velocities:
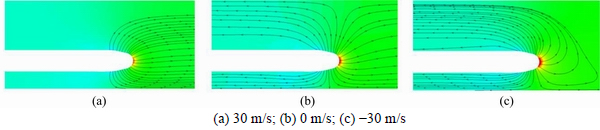
Fig. 17 Streamlines around train head at t=3.6 s under different wind velocities:
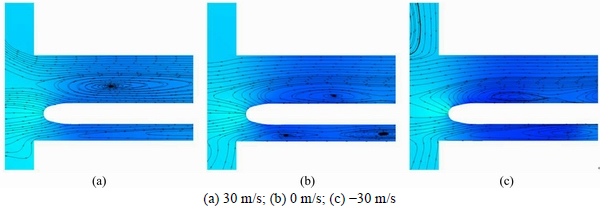
Fig. 18 Streamlines around train tail at t=3.6 s under different wind velocities:
5 Conclusions
1) When the train runs downwind, the strength of pressure waves is reduced. When the train travels against the wind, the strength of pressure waves is reinforced. Compared with the no wind condition, the pressure amplitude of the measuring point 1 on the head car is decreased by 10.5%, and the pressure amplitude of the measuring point 20 on the second car is reduced by 13.0% when the wind velocity is 30 m/s. When the wind velocity is -30 m/s, the pressure amplitude is increased by 17.7% and 17.3% for the measuring points 1 and 20, respectively.
2) The pressure amplitude change is more sensitive under the upwind condition than under the downwind condition. When the wind velocity is -30 m/s, the change rates of pressure amplitudes of all measuring points are more than 16%, and the pressure amplitude at 100 m away from the tunnel entrance changes significantly, and is increased by 20.4%. When the wind velocity is 30 m/s, the most obvious change occurs at 1150 m away from the tunnel entrance, where the pressure amplitude is decreased by 14.4%. Thus, aerodynamic effects will deteriorate if the train runs against the wind in the tunnel.
3) Ambient wind changes the pressure wave strength and its waveform. The time required for the pressure to increase from zero to the maximum positive peak at 1150 m away from the tunnel entrance is reduced by 0.06 s when the wind velocity is 30 m/s, and the time is increased by 0.072 s when the wind velocity is -30 m/s, compared with the no wind condition.
References
[1] ZHANG Lei, TIAN Hong-qi, YANG Ming-zhi, ZHANG Jian, ZENG Xiang-kun, YANG Zhi-gang. Influence on tunnel aerodynamic effects by slope of hat oblique tunnel portal [J]. Journal of Central South University: Science and Technology, 2013, 44(2): 818-822. (in Chinese)
[2] RICCO P, BARON A, MOLTENI P. Nature of pressure waves inducedbyahigh-speedtraintravelling throughatunnel [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(8): 781-808.
[3] HOWE M S, LIDA M. Influence of separation on the compression wave generated by a train entering a tunnel [J]. International Journal of Aero Acoustics, 2003, 2(1): 13-33.
[4] MURRAY P R, HOWE M S. Influence of hood geometry on thecompressionwavegeneratedbyahigh-speedtrain [J]. Journal of Sound and Vibration, 2010, 329(14): 2915-2927.
[5] YANG Ming-zhi, TIAN Hong-qi, YUAN Xian-xu. A new calculation method for micro-pressure waves induced by high-speed train passing through long tunnels [J]. Progress in Computational Fluid Dynamics, 2015, 15(5): 269-278.
[6] BARON A, MOLTENI P, VIGEVANO L. High-speed trains: Prediction ofmicro-pressurewaveradiationfromtunnelportals [J]. Journal of Sound and Vibration, 2006, 296(1, 2): 59-72.
[7] MOK J K, YOO J. Numerical study on high speed train and tunnel hood interaction [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(2): 17-29.
[8] FUKUDA T, OZAWA S, LIDA M. Distortion of compression wave propagating through very long tunnel with slab tracks [J]. JSME International Journal Series B-Fluids and Thermal Engineering, 2006, 49(4): 1156-1164.
[9] SHIN C H, PARK W G. Numerical study of flow chracteristics of the high speed train entering into a tunnel [J]. Mechanics Research Communications, 2003, 30(4): 287-296.
[10] LIU Tang-hong, TIAN Hong-qi, JIN Xue-song. Experimental study of full-scale train on aerodynamics in tunnel [J]. Acta Aerodynamica Sinica, 2008, 26(1): 42-46. (in Chinese)
[11] UYSTEPRUYST D, WILLIAN-LOUIS M, CREUSE E, NICAISE S, MONNYER S. Efficient 3D numerical prediction of the pressure wave generated by hig-speed trains entering tunnels [J]. Computer and Fluids, 2011, 47(3): 165-177.
[12] RABANI M, FAGHIH A K. Numerical analysis of airflow around a passenger train entering the tunnel [J]. Tunneling and Underground Space Technology, 2015, 45(1): 203-213.
[13] KIKUCHI K, LIDA M, FUKUDA T. Optimization of train nose shape for reducing micro-pressurewaveradiated from tunnel exit [J]. Journal of Low Frequency Noise Vibration and Active Control, 2011, 30(1): 1-19.
[14] BS EN 14067-5. Railway applications—Aerodynamics Part 5: Requirements and test procedures for aerodynamics in tunnels [S]. London: British Standard Institute, 2010.
[15] TIAN Hong-qi. Train aerodynamics [M]. Beijing: China Railway Press, 2007: 30-32. (in Chinese)
[16] LIU Tang-hong, TIAN Hong-qi, LIANG Xi-feng. Aerodynamic effects caused by trains entering tunnels [J]. Journal of Transportation Engineering-ASCE, 2010, 136(9): 846-853
[17] CHEN Dan, HAN Kai-feng, ZENG Xin-wu. Numerical modeling of sound wave propagation in wind field using the staggered-grid pseudo-spectral method [J]. Technical Aeousties, 2009, 28(5): 217-218. (in Chinese)
(Edited by DENG Lü-xiang)
Cite this article as: ZHOU Xi-sai, LIU Tang-hong, CHEN Zheng-wei, ZOU Xiang, LIU Dong-run. Effect of ambient wind on pressure wave generated by high-speed train entering a tunnel [J]. Journal of Central South University, 2017, 24(6): 1465-1475. DOI: 10.1007/s11771-017-3550-5.
Foundation item: Projects(U1134203, 51575538)supported by the National Natural Science Foundation of China; Project(2014T001-A) supported by the Technological Research and Development Program of China Railways Corporation; Project(2015ZZTS210) supported by the Fundamental Research Funds for the Central South Universities of China
Received date: 2016-01-18; Accepted date: 2016-04-05
Corresponding author: LIU Tang-hong, Associate Professor;Tel: +86-731-82655294;E mail: lthjd@163.com

