渗流效应对基于广义非线性屈服准则洞室弹塑性解的影响
黄 阜，杨小礼
(中南大学 土木建筑学院，湖南 长沙，410075)
摘 要：考虑渗流效应，基于广义Hoek-Brown非线性屈服准则，推导出圆形洞室围岩塑性区半径、洞壁径向位移和洞室周边径向应力的数值解。绘制在考虑渗流的情况下和基于广义Hoek-Brown屈服准则的不同围岩条件下，圆形洞室内外水头差h与R/e(R为塑性区半径，e为洞室半径)的关系曲线、围岩特性曲线和径向应力的分布曲线。研究结果表明：在水头差相同时，位于较差围岩中洞室的塑性区比位于较好围岩中洞室的塑性区发展快；在支护力相同时，支护结构对处于较差围岩中的圆形洞室洞壁位移约束效果较差；在围岩质量较差时，渗流效应对圆形洞室径向应力的影响比围岩质量较好时的影响大。
关键词：广义Hoek-Brown屈服准则；渗流效应；塑性区半径；水头差；围岩特性曲线
中图分类号：TU921 文献标志码：A 文章编号：1672-7207(2009)06-1737-07
Influence of seepage effect on solutions for elastic and plastic around an opening based on generalized nonlinear yield criterion
HUANG Fu, YANG Xiao-li
(School of Civil and Architectural Engineering, Central South University, Changsha 410075, China)
Abstract: Based on generalized Hoek-Brown yield criterion, and taking into the effect of seepage account, the numerical solution for radius of plastic zone, radial displacement of tunnel wall and stresses around circular opening were derived. The relation curve between hydraulic head pressure difference h and radius of plastic zone R/e around circular opening for different types of rock masses, ground reaction curve, and distribution curve of radial stress based on generalized Hoek-Brown yield criterion were obtained with seepage being considered. The results show that with the same hydraulic head pressure difference, the plastic zone develops faster in the poor quality rock masses than that in good quality rock masses. For poor quality rock masses, the confinement effect on supporting structure for radial displacement of tunnel wall around circular opening is worse when the supporting force is the same. The influence of seepage effect on radial stress around circular opening is more significant in poor quality rock mass than in good quality rock mass.
Key words: generalized Hoek-Brown yield criterion; seepage effect; radius of plastic zone; hydraulic head pressure difference; ground reaction curve
圆形洞室(隧道)在地下工程中的应用十分广泛，大量的盾构隧道、海底隧道、水电引水隧道及矿山竖井中有圆形断面，一些其他形式的地下洞室断面也可近似看作圆形断面处理，因此，在各向同性岩体介质中对圆形洞室的应力—应变进行分析是岩土工程中的一个重要问题。经典的圆形洞室弹塑性解[1-3]采用的都是线性的Mohr-Coulomb屈服准则，然而，实验证明，岩土材料的强度包络线不是线性的，于是，非线性的屈服准则开始应用于圆形洞室的弹塑性计算[4-6]。在这些非线性的屈服准则中，Hoek-Brown屈服准则反映了岩体的固有特点和非线性破坏特征，并且可以准确地预测节理岩体的强度[7]，因而，在隧道和岩土工程界应用十分广泛。Park等[8]在考虑弹性应变增量和塑性区剪胀角变化的影响基础上，采用Hoek-Brown屈服准则绘制了圆形洞室在应变软化介质中的围岩特性曲线，并基于4种不同剪胀角和软化参数研究了弹性应变增量和塑性区剪胀角变化对围岩塑性区的影响。Lee等[9]采用一种简化的数值方法计算了考虑应变软化的Mohr-Coulomb和Hoek-Brown围岩介质中圆形洞室的应力和位移分布。计算结果表明，在粘弹性和应变软化的情况下，采用这种方法计算的应力和位移与解析解较一致。上述圆形洞室的应力—应变分析都是在不考虑地下水渗流的情况下进行的，而地下水是岩体赋存的环境因素之一，尤其是位于高水头富水环境中的深埋洞室更容易发生突水、涌水等事故，因此，地下水渗流对洞室稳定性的影响不可忽略。李宗利等[10]将渗透力以体积力的方式作用在应力场，求解得到弹性位移和应力解析表达式，再应用Mohr-Coulomb屈服准则求解得到塑性应力和塑性半径的解析表达式。Lee等[11]基于Mohr-Coulomb屈服准则，在考虑渗透力的情况下推导出圆形洞室围岩应力和位移分布的解析解和塑性区半径，并且得出围岩特性曲线的简化解。荣传新等[12-13]也考虑了地下水渗流对地下洞室稳定性的影响。目前，人们采用广义Hoek-Brown非线性屈服准则对圆形洞室进行应力—应变分析都没有考虑地下水渗流效应的影响，而考虑地下水渗流的研究又都采用的是线性的Mohr-Coulomb屈服准则，综合考虑广义Hoek-Brown非线性屈服准则和地下水渗流效应的圆形洞室弹塑性分析未见文献报道。为此，本文作者在考虑地下水渗流的基础上，采用广义Hoek-Brown非线性屈服准则，推导出圆形洞室围岩塑性区半径、洞壁径向位移和洞室周边径向应力的数值解，并讨论不同围岩情况下渗流效应对圆形洞室应力和位移分布的影响。
1 基本假设
设无限大均质弹性体内有1个圆形洞室，如图1所示。洞室半径为e，塑性区半径为R，弹性区半径为b，渗流场静水压力为pf，上覆土层自重应力为σh，开挖面支护力为pw，内水水头高度为ha，足够远处的水头高度为h0。为了定性地研究渗透力对洞室围岩应力和位移分布的影响，在推导过程中，对实际问题进行如下假设[14]：
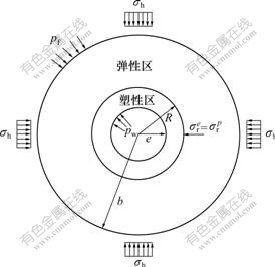
图1 圆形洞室分析模型
Fig.1 Analytical model for circular opening
a. 视围岩为各向同性的等效连续渗透介质；
b. 设渗流场静水压力和上覆土层自重应力沿径向均匀分布且在同一半径上相等；
c. 洞室围岩介质服从广义Hoek-Brown屈服准则，计算时按平面应变情况考虑；
d. 开挖面支护力pw沿开挖面径向均匀分布。
2 广义的Hoek-Brown屈服准则
Hoek-Brown屈服准则最早于1980年由Hoek和Brown提出，20世纪90年代Hoek又提出了广义的Hoek-Brown屈服准则，其表达式[15]如下：
3 考虑渗流情况下圆形洞室应力和位移的理论解
3.1 渗流场分析
假定无限大介质各处渗透系数在各个方向相同，渗流方向主要以径向为主，故本文中所涉及的渗流问题可看作轴对称恒定渗流问题[10]。根据地下水连续性方程及达西定律，由地下水渗流产生的径向渗透力Fr可由下式确定：
3.2 考虑渗流情况下圆形洞室的应力分布和塑性区半径
由弹性力学原理可得考虑渗透力作用的平衡微分方程为：
由于式(5)为非线性微分方程，无法求得解析解，本文根据文献[15]，选取了较好、中等和较差3种围岩质量下的Hoek-Brown参数，`采用数值软件Matlab计算圆形洞室径向应力
的数值解，结果见图2。
1—围岩质量较好；2—围岩质量中等；3—围岩质量较差
图2 3种不同围岩条件下径向应力σr的数值解
Fig.2 Numerical solution of σr for three different types of rock masses
弹性区应力分布[12]为：
将式(9)得出的数值解代入式(8)可求得塑性区半径的数值解。
3.3 考虑渗流情况下圆形洞室的位移分布
Sharan[15]基于广义的Hoek-Brown屈服准则推导了圆形洞室塑性区径向位移分布的表达式，本文在其基础上考虑渗透力的影响，推导出考虑渗流效应情况下圆形洞室的位移解。应变方程为：
对式(16)进行微分，并将式(5)代入得：
弹性区的弹性切向应变为：
式中：f(r)由式(21)确定；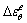
由式(27)确定；
为图1所示的径向应力数值解。
4 计算与讨论
4.1 洞室内、外水头差对洞室塑性区半径的影响
为了分析洞室内、外水头差对洞室塑性区半径的影响，在上覆岩层为100 m、不考虑支护力的情况下，绘制不同围岩条件下圆形洞室内外水头差h=ha-h0与R/e的关系曲线，如图3所示。Sharan[15]根据岩体强度GSI的不同，将围岩分为5类，GSI越高，则围岩越好。由图3可见，随着洞室内外水头差h的增加，塑性区域呈非线性增长的趋势；当h=10 MPa时，GSI=30对应的塑性区半径比GSI=40对应的塑性区半径增加了2.9倍，而GSI=40对应的塑性区半径比GSI=50对应的塑性区半径只增加了2.4倍。因此，在水头差相同的情况下，位于较差围岩中的洞室塑性区比位于较好围岩中的洞室塑性区发展快，并且这一趋势随着水头差的增大而增大。
GSI: 1—50; 2—40; 3—30
图3 不同围岩情况下h与R/e的关系曲线
Fig.3 Relationships between h and R/e for different types of rock masses
4.2 支护力对洞壁位移的影响
为了分析在渗透力作用下洞室支护力对洞壁径向位移的影响，绘制不同围岩情况下的围岩特性曲线，如图4所示，其中：横坐标pw为洞室内壁支护力，纵坐标ur为洞壁径向位移。从图4可以看出，随着GSI的下降，围岩特性曲线向右移动，说明在支护力相同的条件下，围岩质量越差，则洞壁径向位移越大。在支护力相同的情况下，GSI=75对应的洞壁径向位移比GSI=50对应的洞壁径向位移平均减少了14.65%，而GSI=20对应的洞壁径向位移只比GSI=10对应的洞壁径向位移平均减少5.53%。这说明在渗透力作用下，当围岩质量较好时，支护结构对减少洞壁位移、提高围岩承载力的效果比较明显；而当围岩质量较差时，支护结构对减少洞壁位移、提高围岩承载力的效果减弱。因此，在围岩较差的地带开挖隧道和地下洞室，还应采用各种辅助施工方法，以配合支护结构限制洞壁的径向位移。
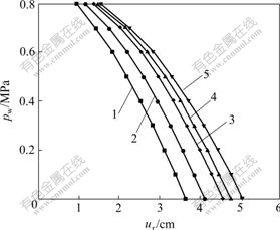
GSI: 1—75; 2—50; 3—30; 4—20; 5—10
图4 不同围岩情况下围岩特性曲线
Fig.4 Ground response curves for different types of rock masses
4.3 渗流对不同围岩条件下圆形洞室径向应力分布的影响
图5所示为在考虑地下水渗流和不考虑地下水渗流，岩体强度指标GSI分别为50和30这2种情况下圆形洞室径向应力的分布曲线。其中，考虑地下水渗流的曲线根据本文推导的公式绘制，而不考虑地下水渗流的曲线根据Sharan[15]推导的公式绘制。从图5可以看出，当岩体强度指标GSI相同，即围岩条件一样时，不考虑渗流情况下的圆形洞室径向应力大于考虑渗流情况下的径向应力；在岩体强度指标较高的情况下，考虑渗流和不考虑渗流的圆形洞室径向应力都大于岩体强度指标较低时的径向应力。
1—GSI=50，不考虑渗流；2—GSI=50，考虑渗流；3—GSI=30，不考虑渗流；4—GSI=30，考虑渗流
图5 不同围岩情况下径向应力σr的分布曲线
Fig.5 Distribution curve of radial stress σr for different types of rock masses
5 结 论
a. 在考虑地下水渗流的情况下，基于广义Hoek-Brown非线性屈服准则，推导了圆形洞室塑性区径向应力、塑性区半径和洞壁径向位移的数值解。
b. 在水头差相同的情况下，位于较差围岩中洞室的塑性区比位于较好围岩中洞室的塑性区发展快；在支护力相同的情况下，支护结构对处于较差围岩中的圆形洞室洞壁位移的约束效果较差。由此可见，渗流效应加剧了圆形洞室开挖后形成的二次应力场以及位移场对原始地应力场分布和位移场的影响，尤其是当圆形洞室位于围岩较差的地带时，这一影响更加显著。
c. 当GSI=50，r相同时，不考虑地下水渗流和考虑地下水渗流时圆形洞室径向应力的平均差为34%；而当GSI=30，r相同时，不考虑地下水渗流和考虑地下水渗流时圆形洞室径向应力的平均差为66%。由此可见，渗流效应对圆形洞室径向应力的影响在围岩质量较差时比围岩质量较好时的大。因此，在围岩情况较差的富水地带开挖隧道和地下洞室时，应注意地下水的渗流效应。
参考文献：
[1] 郑雨天. 岩石力学的弹塑粘性理论基础[M]. 北京: 煤炭工业出版社, 1988.
ZHENG Yu-tian. Fundamentals of elastic-plastic-sticky theory of rock mechanics[M]. Beijing: China Coal Industry Press, 1988.
[2] 蔡美峰, 何满潮, 刘东燕. 岩石力学与工程[M]. 北京: 科学出版社, 2002.
CAI Mei-feng, HE Man-chao, LIU Dong-yan. Rock mechanics and engineering[M]. Beijing: Science Press, 2002.
[3] 凌贤长, 蔡得所. 岩体力学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2002.
LING Xian-chang, CAI De-suo. Rock mechanics[M]. Harbin: Harbin Institute of Technology Press, 2002.
[4] 潘 岳, 王志强. 基于应变非线性软化的圆形硐室围岩弹塑性分析[J]. 岩石力学与工程学报, 2005, 24(6): 915-920.
PAN Yue, WANG Zhi-qiang. Elasto-plastic analysis on surrounding rock of circular chamber based on strain nonlinear softening[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(6): 915-920.
[5] Sharan S K. Elasto-brittle-plastic analysis of circular opening in Hoek-Brown media[J]. Int J Rock Mech Min Sci, 2003, 40(6): 817-824.
[6] SUN Jin-shan, LU Wen-bo, ZHU Qi-hu, et al. Elasto-plastic analysis of circular tunnels in jointed rock masses satisfy the Hoek-Brown failure criterion[J]. Journal of China University of Mining and Technology, 2007, 17(3): 393-398.
[7] 林 杭, 曹 平, 赵延林, 等. 强度折减法在Hoek-Brown准则中的应用[J]. 中南大学学报: 自然科学版, 2007, 38(6): 1219-1224.
LIN Hang, CAO Ping, ZHAO Yan-lin, et al. Application of strength reduction method in Hoek-Brown criterion[J]. Journal of Central South University: Science and Technology, 2007, 38(6): 1219-1224.
[8] Park K H, Tontavanich B, Lee J G. A simple procedure for ground response curve of circular tunnel in elastic-strain softening rock masses[J]. Tunnelling and Underground Space Technology, 2008, 23(2): 151-159.
[9] Lee Y K, Pietruszczak S. A new numerical procedure for elasto-plastic analysis of a circular opening excavated in a strain-softening rock mass[J]. Tunnelling and Underground Space Technology, 2008, 23(5): 588-599.
[10] 李宗利, 任青文, 王亚红. 考虑渗流场影响深埋圆形隧洞的弹塑性解[J]. 岩石力学与工程学报, 2004, 23(8): 1291-1295.
LI Zong-li, REN Qing-wen, WANG Ya-hong. Elasto-plastic analytical solution of deep-buried circle tunnel considering fluid flow field[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(8): 1291-1295.
[11] Lee S W, Jung J W, Nam S W, et al. The influence of seepage forces on ground reaction curve of circular opening[J]. Tunneling and Underground Space Technology, 2006, 21(1): 28-38.
[12] 荣传新, 程 桦. 地下水渗流对巷道围岩稳定性影响的理论解[J]. 岩石力学与工程学报, 2004, 23(5): 741-744.
RONG Chuan-xin, CHENG Hua. Stability analysis of rocks around tunnel with ground water permeation[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(5): 741-744.
[13] Kolymbas D, Wagner P. Groundwater ingress to tunnels—The exact analytical solution[J]. Tunnelling and Underground Space Technology, 2007, 22(1): 23-27.
[14] Wang Y. Ground response of circular tunnel in poorly consolidated rock[J]. ASCE Journal of Geotechnical and Geoenvironmental Engineering, 1996, 122(9): 703-708.
[15] Sharan S K. Analytical solution for stress and displacements around a circular opening in a generalized Hoek-Brown rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 23(1): 78-85.
收稿日期：2008-12-23；修回日期：2009-03-15
基金项目：交通部西部建设科技项目(200631878557)；中南大学优秀博士学位论文扶持项目(2009ybfz19)
通信作者：黄 阜(1983-)，男，湖南岳阳人，博士研究生，从事地下工程稳定性研究；电话：13975146439；E-mail: hfzndx2002@yahoo.com.cn
