Dual-resource integrated scheduling method of AGV and machine in intelligent manufacturing job shop
来源期刊:中南大学学报(英文版)2021年第8期
论文作者:苑明海 李亚东 裴凤雀 顾文斌
文章页码:2423 - 2435
Key words:dual resource integrated scheduling; improved A* algorithm; improved NSGA-II algorithm; competition mechanism
Abstract: In view of the fact that traditional job shop scheduling only considers a single factor, which affects the effect of resource allocation, the dual-resource integrated scheduling problem between AGV and machine in intelligent manufacturing job shop environment was studied. The dual-resource integrated scheduling model of AGV and machine was established by comprehensively considering constraints of machines, workpieces and AGVs. The bidirectional single path fixed guidance system based on topological map was determined, and the AGV transportation task model was defined. The improved A* path optimization algorithm was used to determine the optimal path, and the path conflict elimination mechanism was described. The improved NSGA-II algorithm was used to determine the machining workpiece sequence, and the competition mechanism was introduced to allocate AGV transportation tasks. The proposed model and method were verified by a workshop production example, the results showed that the dual resource integrated scheduling strategy of AGV and machine is effective.
Cite this article as: YUAN Ming-hai, LI Ya-dong, PEI Feng-que, GU Wen-bin. Dual-resource integrated scheduling method of AGV and machine in intelligent manufacturing job shop [J]. Journal of Central South University, 2021, 28(8): 2423-2435. DOI: https://doi.org/10.1007/s11771-021-4777-8.

J. Cent. South Univ. (2021) 28: 2423-2435
DOI: https://doi.org/10.1007/s11771-021-4777-8
YUAN Ming-hai(苑明海)1, 2, LI Ya-dong(李亚东)1, 2, PEI Feng-que(裴凤雀)1, GU Wen-bin(顾文斌)1
1. School of Mechanical and Electrical Engineering, Hohai University, Changzhou 213000, China;
2. Institute of Marine and Offshore Engineering, Hohai University, Nantong 226300, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Abstract: In view of the fact that traditional job shop scheduling only considers a single factor, which affects the effect of resource allocation, the dual-resource integrated scheduling problem between AGV and machine in intelligent manufacturing job shop environment was studied. The dual-resource integrated scheduling model of AGV and machine was established by comprehensively considering constraints of machines, workpieces and AGVs. The bidirectional single path fixed guidance system based on topological map was determined, and the AGV transportation task model was defined. The improved A* path optimization algorithm was used to determine the optimal path, and the path conflict elimination mechanism was described. The improved NSGA-II algorithm was used to determine the machining workpiece sequence, and the competition mechanism was introduced to allocate AGV transportation tasks. The proposed model and method were verified by a workshop production example, the results showed that the dual resource integrated scheduling strategy of AGV and machine is effective.
Key words: dual resource integrated scheduling; improved A* algorithm; improved NSGA-II algorithm; competition mechanism
Cite this article as: YUAN Ming-hai, LI Ya-dong, PEI Feng-que, GU Wen-bin. Dual-resource integrated scheduling method of AGV and machine in intelligent manufacturing job shop [J]. Journal of Central South University, 2021, 28(8): 2423-2435. DOI: https://doi.org/10.1007/s11771-021-4777-8.
1 Introduction
In recent years, people have gradually realized the importance of the manufacturing industry, and many countries have formulated strategic plan to support the development of the manufacturing industry. The competition among manufacturing enterprises has become increasingly fierce [1, 2]. Improving production management is one of the effective ways for companies to improve their competitiveness, and the reasonable allocation of job shop resources is the core of production management [3]. The purpose of reducing cost, improving quality, increasing efficiency, low carbon and energy saving can be achieved by reasonably scheduling the job shop resources. In the traditional discrete scheduling environment, only one problem is considered, which is the allocation relationship between the workpiece and the machine tool, and then the algorithms is used to solve it. For example, LI et al [4] analyzed the energy consumption in the workshop production, and used the simulated annealing algorithm to solve the problem with the goals of minimizing energy consumption and makespan, and realized the flexible batch optimization scheduling of multiple process routes. GAO et al [5] proposed a hybrid particle swarm optimization algorithm based on variable neighborhood search to solve the flexible job-shop scheduling problem (FJSP) problem. LU et al [6] studied the multi-objective FJSP with controllable processing times, and proposed a new multi-objective discrete virus optimization algorithm with a three-part representation, and combined the experimental results which demonstrate the efficiency of the algorithm. In addition, artificial bee colony algorithm [7], gray wolf optimization algorithm [8], fruit fly optimization [9], whale colony algorithm [10], water wave optimization algorithm [11] are also used to solve the job shop scheduling problem.
In intelligent manufacturing environment, the production relationship is more complicated, and only considering a single factor will affect the effect of resource allocation. Some experts and scholars have begun to consider other factors to study the multi-resource integrated scheduling problem. XIAO [12] considered the constraints of worker restrictions, and combined the chemical reaction algorithm and the variable neighborhood search algorithm to solve the dual-resource flexible job shop scheduling model. LI et al [13] considered the worker factor and used genetic algorithm to solve the dual-resource flexible job shop scheduling problem. ZHOU et al [14] established a mathematical model that can describe the operation, personnel, and equipment for the aerospace structural parts scheduling process, and designed a nested ant colony-genetic algorithm with the goal of total completion time and equipment utilization. CHEN et al [15] combined particle swarm algorithm and differential evolution algorithm to study the dual resource constraint multi-assembly line scheduling problem under the condition of order uncertainty. ZHANG et al [16] also studied the dual resource scheduling proble, and considered the ability of workers using the hybrid discrete particle swarm optimization algorithm. WU et al [17] considered the problem that the machines need frequent maintenance during service, and designed a super-heuristic cultural genetic algorithm to solve the integrated scheduling optimization model. As the production mode shifts from mass standardized production to multi-variety and small-batch individualization, the transportation time of workpieces cannot be ignored. If the transfer time is not considered, the application effect for the job shop scheduling with a precise process processing time will be greatly affected. With the continuous improvement of workshop intelligence, workshop production and logistics have changed from traditional independent operation to integrated linkage. As the key equipment of intelligent production, AGV is widely used in the collaborative work of workshop and machine tool instead of manual transportation. The choice of different AGVs and different paths corresponds to different transfer times, which will affect the starting processing time of the workpiece and the whole production scheduling cycle. Therefore, the problem of dual-resource integrated scheduling between AGV and machine has become one of the current research hotspots. LIU et al [18] adopted an improved flower pollination algorithm to solve the integrated scheduling problem of AGV and machine, but did not consider the AGVs allocation strategy. Aiming at the logistics dynamic scheduling problem of intelligent manufacturing workshop, XU et al [19] proposed an intelligent logistics scheduling model and response method that considered AGV. At the same time, the Internet of Things technology was applied to meet the needs of dynamic and real-time. FONTS et al [20] studied the joint production transportation scheduling problem, established a new mixed-integer linear programming model, integrated machine scheduling problem and AGV scheduling problem, and used the two sets of chain decision strategies (one for machines and the other for AGV) to solve the problem. LYU et al [21] considered the problems about optimal number of AGVs, the shortest transportation time and path planning, and proposed a hybrid algorithm based on GA and Dijkstra algorithm. LI et al [22] proposed an improved harmony search algorithm to solve the mathematical model to minimize AGV buffer waiting time and the total driving distance. UMAR et al [23] considered the path conflict problem and solved it with an improved genetic algorithm, but the algorithm runs for a long time and is inefficient.
In the dual-resource integrated scheduling problem of AGV and machine, the shortest path planning A* algorithm is a typical heuristic search algorithm, which has the advantages of strong stability, simple algorithm and faster solving speed. NSGA-II is one of the most widely used multi-objective optimization algorithms, which has the advantages of simple, effective, good expansibility and easy to combine with other algorithms. Therefore, in this paper, the improved A* algorithm and improved NSGA-II algorithm was used to study the dual-resource integrated scheduling problem. The contributions of this paper are as follows:
1) The integrated scheduling model of AGV and machine was established, and the two-stage integrated scheduling strategy was determined.
2) The NSGA-II algorithm was improved. Firstly, the crossover operator and mutation operator was improved, and the variable probability crossover and mutation was adopted. That is, the probability of crossover and mutation from the first generation to the N-th generation decreased linearly. Secondly, aiming at the shortcomings of the traditional NSGA-II algorithm that is easy to fall into the local optimum in the later stage, in this paper, the traditional elite retention strategy was used in the previous N/3 generations, and from the N/3-th generation to the N-th generation, the variable proportion method was designed to make the proportion of the optimal parent generation in the population linearly decrease with the increase of the iterations number.
3) The AGV transportation task model was defined and the bidirectional single-path fixed guidance system based on topological maps was established. When the improved A* algorithm was used to solve the problem, the number of path turns was less and the time-consuming was shorter.
2 Mathematical modelling
The integrated scheduling problem of AGV and machine in intelligent manufacturing workshop can be described as: there are N workpieces to be processed in a processing system. M machines and V AGVs trolleys can be used for processing. When the workpiece starts to be processed, the AGV first takes out the blank from the three-dimensional warehouse and transports it to the corresponding machine tools for processing (when modelling, the three-dimensional warehouse is regarded as a location point with the same attributes as the machine tool). After this operation is completed, it is transported by AGV to other machine tools for processing, and after all operations of the workpiece is processed, it is transported back to the warehouse by AGV. Each workpiece Ni (i=1, 2, ..., n) contains one or more operations, Oij represents the j-th process of the workpiece Ni, and each operation Oij can be processed by any one of the optional machines set  The processing time of the operation changes with the change of the processing machine, and the operation sequence of the workpiece has been determined in advance. In order to study the workshop scheduling problem in intelligent manufacturing environment, the following constraint assumptions need to be met:
The processing time of the operation changes with the change of the processing machine, and the operation sequence of the workpiece has been determined in advance. In order to study the workshop scheduling problem in intelligent manufacturing environment, the following constraint assumptions need to be met:
1) Each machine can only process one workpiece at the same time, and each workpiece can only be processed by one machine at the same time;
2) Each machine, workpiece and AGV have the same priority, and the processing cannot be interrupted once the workpiece starts to be processed;
3) Each AGV can only transport one workpiece at the same time, and each workpiece can only be transported by one AGV at the same time. And the process of AGV transporting the workpiece will not be interrupted;
4) There is a workpiece buffer area beside each machine tool, but only one AGV can be docked, and multiple AGVs can be docked in the three-dimensional warehouse;
5) The speed of the AGV remains unchanged during the transportation process and is not affected by the load;
6) The initial AGV position and the initial workpiece position are located in the warehouse;
7) The time of AGV loading and unloading workpieces in the warehouse or machine tool buffer is ignored;
8) Each AGV can transport workpieces between any two machines. The AGV stops in the buffer zone of the machine tool without affecting the passage of other AGVs.
The description of relevant symbols involved in the subsequent scheduling model is shown in Table 1.
The mathematical model established in this paper is as follows:
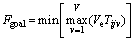 (1)
(1)
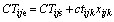 (2)
(2)
 (3)
(3)
Table 1 Symbol description
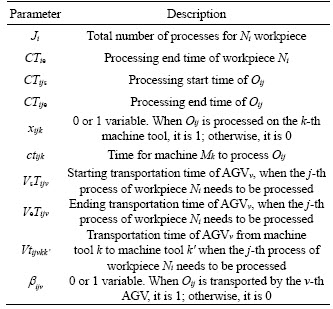
 (4)
(4)
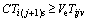 (5)
(5)
 (6)
(6)
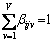 (7)
(7)
Equation (1) shows that the goal is to minimize the maximum completion time of the workpieces return to the warehouse and Fgoal is the objective function. Equation (2) indicates that once the machining process starts, it cannot be interrupted. Equation (3) shows that the AGV can only start the transportation task of the workpiece after the previous operation of the workpiece is completed. Equation (4) means that the transportation process cannot be interrupted. Equation (5) means that the workpiece can not be processed until it is transported. Equation (6) indicates that only one machine can be selected for one operation, the superscript M is the number of the machines. Equation (7) shows that only one AGV can be selected for one task, and also means that at the same time, each machine can only process one workpiece, and each AGV can only transport one workpiece, the superscript V is the number of the AGVs.
3 Dual-resource integrated scheduling strategy
The dual resource integrated scheduling strategy can be divided into two stages [24, 25]. In this paper, the first stage is to determine the machining workpiece sequence with the help of intelligent algorithm, and the second stage is to allocate AGV transportation tasks to realize the transportation of workpieces from warehouse to machine, from machine to machine, and from machine to warehouse.
3.1 Improved NSGA-II
Genetic algorithm is an intelligent optimization algorithm based on natural evolution and selection mechanism. It has the characteristics of global search capability and simple iteration process [26]. The flow chart of the improved NSGA-Ⅱ algorithm is shown in Figure 1.
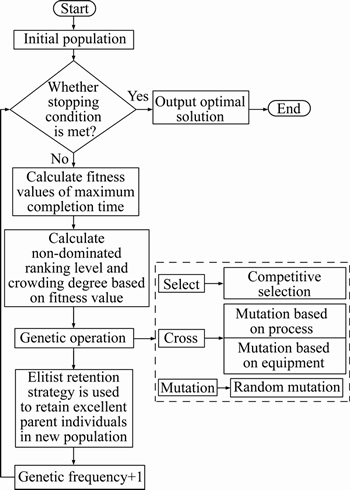
Figure 1 Improved NSGA-II algorithm flowchart
Firstly, the initial population was randomly generated based on the workpiece operation and the corresponding processing machine. The greedy decoding algorithm was used to calculate the maximum completion time of each chromosome, and each chromosome was evaluated according to the ranking level and crowding degree, and the chromosomes for genetic operation were selected by competitive bidding method. The crossover operation and mutation operation based on workpiece process and machine was adopted to generate a new population, and elite retention strategy was used to select the excellent parent individuals in the new population. After the iteration, the optimal solution set was output. The optimal solution set consists of two parts: one is the optimal individual in the N/2-N-1 generation, and the other is the optimal individual in the first 20% of the last generation.
3.1.1 Encoding and decoding
In this paper, a multi-layer coding method based on real number is adopted. Each chromosome represents a feasible solution of the problem to be optimized. The first layer adopts the real number coding based on the workpiece operation process, and the second layer adopts the real number coding based on the processing machine. The length of the two layers is same. The first layer of the workpiece operations is generated randomly, and the second layer of the processing machines is randomly selected from the set of optional machines. As shown in Figure 2, the first gene 6 represents the process O61, which is processed by the machine M2; the 2 on the gene locus 2, 4, and 5 represent the process O21, O22, O23, which are processed by the machines M4, M5, and M4, respectively.

Figure 2 Chromosome encoding diagram
Greedy decoding algorithm is introduced into decoding calculation. For a certain workpiece, the completion time of the previous operation of the workpiece is end_t_p, and the completion time of the last operation of the machine processing is end_t_m. Compared end_t_p with end_t_m, if end_t_p
3.1.2 Competition selection
Two individuals are randomly selected from the population for genetic operation, and the individuals with higher ranking level are preferred. In this algorithm, the ranking level 1 is the highest. If the ranking level is the same, the individual with large crowding degree is preferred; if the crowding degree is the same, one of the individuals is selected randomly.
3.1.3 Crossover operation and mutation operation
In the early stage of evolution, the fitness of chromosomes is poor and requires a large probability of crossover and mutation. In the later stage of evolution, the chromosome has a good structure and requires a small probability of crossover and mutation. Therefore, variable probability crossover and mutation is adopted. That is, the probability of crossover and mutation from the first generation to the N-th generation decreases linearly. In order to show the operation process more clearly, some chromosomes of 6×6 (6 workpieces and 6 machines) are selected to illustrate the crossover and mutation method.
1) Crossover operation
In this paper, the hybrid crossover mode based on workpiece operation process crossover and machine crossover is adopted. The rand function is used to generate random number  If r≤0.5, process-based crossover is adopted; otherwise, machine-based crossover is used. The specific operation is shown in Figure 3.
If r≤0.5, process-based crossover is adopted; otherwise, machine-based crossover is used. The specific operation is shown in Figure 3.
For the process-based crossover, the workpieces are divided into two groups, and the function randi is used to randomly generate a 0,1 matrix R1×N (N is the number of the workpieces). The workpieces with the position 1 in the matrix are a group, and the rest are a group. As shown in Figure 3, assuming that the gene position corresponding to the number 1 is 6, 1, then workpieces 6 and 1 are a group, and workpieces 2, 3, 4 and 5 are a group. The gene of workpiece 6, 1 and the corresponding machine gene in the parent chromosome 1 remains unchanged, the gene of workpiece 2, 3, 4, 5 and the corresponding machine gene in parent chromosome 2 is successively inserted into the remaining gene locus of the parent chromosome 1. In the same way, the gene of workpiece 2, 3, 4, 5 and the corresponding machine gene in the parent chromosome 2 remains unchanged, the gene of workpiece 6,1 and the corresponding machine gene of parent chromosome 1 is successively inserted into the remaining gene locus of the parent chromosome 2.
For the machine-based crossover, a 0,1 matrix is randomly generated; the size of the matrix is equal to the length of the workpiece process chromosome; and the processing machine corresponding to the number 1 in the matrix on the parent chromosome 1 is crossed. Assuming that the gene position corresponding to the number 1 is 2, 6, ..., and the gene position 6 is taken as an example. As shown in Figure 4, the gene locus 6 of the parent chromosome 1 is O11, which is processed by M3, and O11 on parent chromosome 2 is processed by M1. The processing machines of the O11 in the two parent chromosomes are crossed. That is, the O11 in parent chromosome 1 is processed by M1, and the O11 in parent chromosome 2 is processed by M3.

Figure 3 Process-based crossover
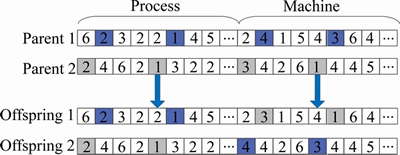
Figure 4 Machine-based crossover
2) Mutation operation
The randperm(P_number,cal) function is adopted to randomly generate chromosome mutation positions, where cal represents the number of chromosome gene mutations. Assuming that one of the mutation positions is the third gene. As shown in Figure 5, the processing machine of O31 is mutated, and the optional machine set of O31 is M1, M4, M5. The processing machine for O31 in the parent chromosome 1 is M1. When the mutation occurs, another machine in the machine set are randomly selected to process O31. For example, machine M4 is selected.

Figure 5 Mutation operation
The improved NSGA-II algorithm has made two improvements. The first is that in the early stage of evolution, the fitness of chromosomes is poor and requires a large probability of crossover and mutation. In the later stage of evolution, the chromosome has a good structure and requires a small probability of crossover and mutation. Therefore, the variable probability crossover and mutation is adopted. That is, the probability of crossover and mutation from the first generation to the N-th generation decreases linearly. The second is that the recessive elite retention strategy is adopted for the traditional NSGA-II. Firstly, the parents and offspring are combined to form the total population Popt. Secondly, the individuals with high rank and high crowding degree is selected from the population Popt according to the fast non-dominated and crowding degree. This method can effectively improve the convergence of genetic algorithm and avoid the loss of the optimal solution in the evolution process. However, the new individuals generated in the population will be repelled in the later stage, which is not conducive to the diversity of the population and easy to make the algorithm fall into local optimum. Therefore, the variable proportion method is designed in this paper. The traditional elite retention strategy is used in the previous N/3 generations, and from the N/3-th generation to the N-th generation, the variable proportion method is designed to make the proportion of the optimal parent generation in the population linearly decrease with the increase of the iterations number.
3.2 AGV path search algorithm
3.2.1 AGV operating environment expression
AGV environment expression refers to mapping the actual physical space into binary virtual space through electronic map modelling, including the information of nodes, paths, distances, workstations, etc [27]. The accuracy of the model obtained by choosing different methods for map modelling is quite different, and it also affects the efficiency of the path planning algorithm. Topological map method is a kind of small redundant and compact environment representation method. Nodes represent the important position points in the workshop, including machine tool positions, intersections, automatic warehouses, etc. The connection between points represents the accessible routes in the actual environment. The weight of the edge represents the length of the path or the cost of passing through the path. The topology map modelling is intuitive and simple, easy to implement and maintain, and is suitable for the structured environment of the workshop. At the same time, according to the actual environment of the workshop, the bidirectional single-path fixed guidance system is adopted.
3.2.2 Transportation task model
When a transportation task is generated, it is defined as follows:
 (8)
(8)
where AGVi represents the reference number of the AGV performing the task; Tcon refers to the task determination time; Lstart represents the starting point of the transportation task; Lend represents the end point of the transportation task; Tstart and Tend represent the transportation start time and end time, respectively; and Pathpij(t) refers to the path.
3.2.3 Improved A* algorithm
A* algorithm is a typical heuristic search algorithm. It relies on the heuristic information to optimize the search strategy, not all feasible solutions are searched, which increases the efficiency of the solution [28]. The evaluation function of A* algorithm is:
 (9)
(9)
where f(p) is the estimated distance value from the AGV transportation starting point s to the AGV transportation terminal t via node p; g(p) is the actual shortest path length from the AGV transportation starting point s to the node p; h(p) is the Self-defined heuristic function, the estimated value of the path length from the node p to the AGV transportation terminal t.
In Eq. (9), the selected value of h(p) is the most important. If the value of h(p) is bigger than the actual distance from the node p to the node t, some nodes will be discarded according to f(p) during the calculation process, and the solution speed will be faster, but the result obtained can only guarantee a better solution. If the value of h(p) is chosen to be less than the actual distance between the two nodes p and t, the search range will be enlarged; the number of nodes searched will be increased; computation will be more complicated; but the optimal solution will eventually be obtained. In order to obtain the optimal solution and reduce the amount of calculation, the heuristic function value should be as equal to the actual distance as possible. In this paper, Manhattan distance is chosen as heuristic function, i.e. h(p)=|xp-xt|+|yp-yt|. The implementation step is shown in Figure 6.
Firstly, table M and table N is initialized. Table M contains the points that have been generated but not evaluated, and table N contains the evaluated nodes. When the path starts to be searched, the transportation starting point s of AGV is placed in M, and N is empty. Then search for the node connected with AGV transportation starting point s and put it into table M. After the evaluation function value is calculated, the minimum value f(j) is found and the corresponding node is moved to table N. If the minimum value is equal, the multiple alternative paths this time are compared with the path formed by the previous two nodes, and the path that enables the AGV to travel straight is selected. Then judge whether the node j is the AGV transportation terminal t, if it is, the search ends; otherwise, the adjacent unsearched node of node j is moved to table M and the corresponding evaluation function value is calculated at the same time. The node with the smallest evaluation value is found in table M and move it to table N, and judge whether the corresponding point of the minimum value is the end point. The production environment is structured in intelligent manufacturing workshop, and the evaluation function value is often equal in the algorithm search process. For the original A* algorithm, a corresponding node is selected randomly. The A* algorithm is improved in this paper. If the evaluation function value is equal, the multiple search paths determined this time are compared with the path formed by the previous two nodes, and the path that enables the AGV to travel in a straight line is selected.
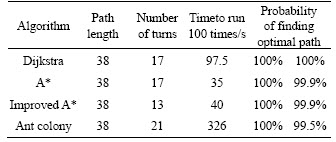
This paper compared the search capabilities of the four algorithms, as shown in Figure 7.
This paper establishes a complex path topology map, where the weight of the adjacent edge between every two points is 1, the AGV starting point is (1,20), and the end point is (20,1). The hardware platform is Intel (R) core (TM) i5-8400 CPU@2.80GHz, RAM 16 GB. The search path of three algorithms are got by using MATLAB 2016b.

Figure 6 Improved A* algorithm flow chart

Figure 7 Schematic diagram of four algorithms search paths
For the four algorithms, it should be noted that the path length, the number of turns, the time taken to run 100 times, and the probability of finding the optimal path are obtained by calculating in Figure 7 (Table 2). The probability of finding the optimal path in the second column in Table 2 is obtained by calculating in a variety of topological map environments. It can be seen from Figure 7 and Table 2 that the four algorithms all can search for the optimal point and have the same path length, the path obtained by using the improved A* algorithm has the least number of turns and is also less time-consuming. Dijkstra algorithm can 100% search the optimal path, but it takes a longer time. Ant colony algorithm takes the longest time, and the probability of finding the optimal path is less than the other two algorithms. Therefore, this paper will finally choose the improved A* algorithm as the path optimization algorithm.
Table 2 Algorithms comparison
3.2.4 Path conflict elimination method
In the AGV scheduling system, there is no need to consider the path conflict problem; planning the path according to the desired goal is needed. For the multi-AGV workshop scheduling, if the path planning for each AGV is independent, there will be path conflicts and system deadlock. Therefore, in the multi-AGV scheduling, the path conflict elimination strategy needs to be added [29]. In this paper, based on the time window method, the principle of the first task path unchanged is adopted, that is, if the path of the subsequent task conflicts with the path of the previous task, the previously determined path remains unchanged. Then the time to reach the destination is calculated by using the waiting strategy and the task path re-planning strategy, respectively, and the less time-consuming conflict resolution strategy is adopted. If the time consumption of the two strategies is the same, the waiting path elimination strategy is preferred.
During the operation of the integrated scheduling system, AGV1 first arrives at machine tool Mk, and then AGV2 also transports another workpiece to reach the machine tool Mk. Since the machine buffer Mk can only be docked one AGV, the AGV1 with no task will be transferred to the nearest machine free buffer or warehouse to wait for new transportation tasks.
3.3 Assign AGV transportation tasks
1) The optimal solution set contains multiple individuals. For each individual processing sequence, the AGV first executes the “double one” request task, that is, the first operation of the workpiece is processed on this machine and the first task of this machine is to process the workpiece. If there are multiple “double one” request tasks, the less time consuming is transported first. At the beginning, AGVs are all not in a working state, and they are in the same position. Therefore, the order of AGV deployment will be formed randomly. After the “double one” request task is completed, then the AGV executes “single one” request task, that is, the first process of the workpiece is processed on this machine. Finally, all the workpieces are transported out of the warehouse.
2) The earliest transportable time of all workpieces is compared to form the earliest transportable time set, and the minimum value of the earliest transportable time set is found. The workpiece corresponding to the minimum value is the task to be transported, and the transportation starting point and ending point of the task are obtained according to the sequence of the machine processing workpiece.
3) Each AGV competes for the task and calculates the time to reach the starting point of the task. The improved A* algorithm is used to calculate the path from the current position of each AGV to the transportation starting point, and judge whether it conflicts with the existing task path. If it is, the task elimination strategy is adopted. Then the walking path and walking time of each AGV is calculated. If there is an AGV that arrives before the transportation time point, then choose the AGV that consumes less time; if not, choose the AGV that reaches to the transportation starting point earliest. When the AGV reaches the starting point of the transportation task, the starting point, ending point, starting time, ending time, walking path and key points of it are recorded and stored. Then, according to the starting point, ending point and starting time of the transportation task, the improved A* algorithm is used to calculate the path and the time passing through the key points to judge whether there is any conflict. If there is, the path elimination strategy is adopted. Finally, the starting point, ending point, starting time, ending time, walking path and key points of the AGV that transport this task are recorded and stored.
4) Repeat 2) to 3) until the last workpiece is transported back to the warehouse.
4 AGV integrated scheduling test verification
For the integrated scheduling, there may be multiple task time windows on a path. Most researches stipulate that only one AGV can be driven on one path at the same time, which will lead to a waste of lane resources, especially in long lanes. According to the actual situation of intelligent workshop transportation, this paper stipulates that two AGVs can travel on the same path and maintain the shortest distance L. Then, according to the travel speed Vagv, the time T between two AGVs on the same path can be calculated.
The electronic map of this test is shown in Figure 8, there are 6 machine tools, 2 AGVs and one three-dimensional warehouse. The distance between two machine tools in horizontal direction is 15 m; the distance between two horizontal roads is 10 m; and the distance between two longitudinal adjacent roads is 15 m. It is stipulated that the minimum distance between two AGVs on each road section is L=2.5 m, and the driving speed of the AGV is Vagv=0.25 m/s. The basic parameters of the improved NSGA-II algorithm proposed in this paper are set as follows: the initial population size NIND is 200; the maximum iteration number Maxgen is 50; the crossover probability Pc is 0.8→0.4; and the mutation probability Pv is 0.1→0.02. The operations of 6 workpieces and the precisely set processing time on different machines are shown in Table 3. The workpieces J1, J3, J4 and J6 each have 3 operations; and the workpieces J2 and J5 each have 4 operations; “—” in the table means that the operation of the workpiece cannot be processed on the corresponding machine. The obtained Gantt chart is shown in Figure 9. And the maximum completion time is 2900 s. The comparison result with the three encoding chain scheduling strategy (TECS) in Ref. [30] is shown in Figure 10. In order to detect the significance difference of results, the statistical Z-test is conducted, the value of Z is calculated according to Eq. (10):
 (10)
(10)
where 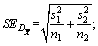
 is the mean of the data; s is the standard deviations of the data; n is the number of data. The result of the statistical Z-test is as shown in Table 4, the confidence level is 0.05.
is the mean of the data; s is the standard deviations of the data; n is the number of data. The result of the statistical Z-test is as shown in Table 4, the confidence level is 0.05.

Figure 8 Job shop electronic map
It can be seen from Table 4, Figures 9 and 10 that the shortest processing time of this processing task is 2900 s. The algorithm designed in this paper can obtain a better solution with higher stability and a small floating range. In the case of the same population size and iteration times, the efficiency and correctness of the results of the three encoding chain scheduling algorithm are not as good as the algorithm proposed in this paper, the confidence level of 0.05 corresponds to the Z-value of 1.64, the Z-value calculated in this paper is 4.54, which is much bigger than 1.64, verifying the effectiveness and significance of the algorithm and strategy designed in this paper.
Table 3 Data of intelligent manufacturing job shop scheduling

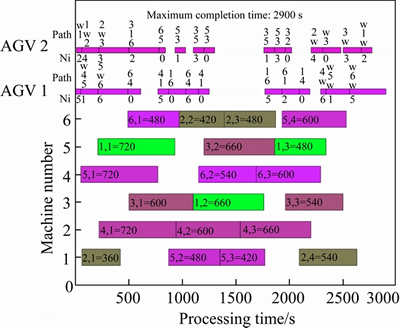
Figure 9 6×6 integrated scheduling diagram
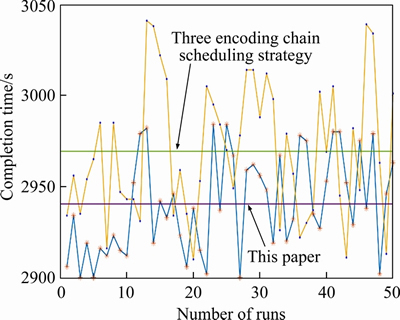
Figure 10 Comparison result
Table 4 Comparison of solution results

5 Conclusions
A two-stage method for dual-resource integrated scheduling problem in intelligent manufacturing job shop is presented. Based on the bi-directional single path fixed guidance system of topological map, the AGV transportation task model is established, and the improved A* algorithm is used to determine the optimal path. The comparison with other algorithms shows that the path obtained by the improved A* algorithm with the least number of turns and less time-consuming. On this basis, the NSGA-II algorithm is improved, and the competition mechanism is introduced to allocate AGV transportation tasks. Integrated scheduling experiments is conduct on the developed method, and the result shows that the algorithm designed in this paper can obtain a better solution with higher stability and a small floating range. In summary, the main work of this paper is to provide a relatively reliable method for dual-resource scheduling problem. In this paper, some factors are not considered for convenience, such as the time consumption of AGV loading and unloading. To further enhance the practicability of this method, the authors hope to establish an integrated scheduling model more in line with the actual production of intelligent workshop.
Contributors
The overarching research goals were developed by YUAN Ming-hai and PEI Feng-que. YUAN Ming-hai and LI Ya-dong carried out conceptualization, methodology, software, investigation, visualization, validation, writing-original draft. GU Wen-bin conducted the literature review. LI Ya-dong edited the draft of manuscript.
Conflict of interest
YUAN Ming-hai, LI Ya-dong, PEI Feng-que, and GU Wen-bin declare that they have no conflict of interest.
References
[1] ZHOU Ji. Intelligent mannfacturing—Main direction of “Made in China 2025” [J]. China Mechanical Engineering, 2015, 26(17): 2273-2284. DOI: 10.3969/j.issn.1004-132X. 2015.17.001.
[2] YAO Xi-fan, JIN Hong, ZHANG Jie. Towards a wisdom manufacturing vision [J]. International Journal of Computer Integrated Manufacturing, 2015, 28(12): 1291-1312. DOI: 10.1080/0951192X.2014.972462.
[3] YUAN Ming-hai, DENG Kun, CHAOVAlITWONGSE W A, CHENG Shuo. Multi-objective optimal scheduling of reconfigurable assembly line for cloud manufacturing [J]. Optimization Methods and Software, 2017, 32(3): 581-593. DOI: 10.1080/10556788.2016.1230210.
[4] LI Cong-bo, SHEN Hua, LI Ling-ling, LI Qian. A batch splitting flexible job shop scheduling model for energy saving under alternative process plans [J]. Journal of Mechanical Engineering, 2017, 53(5): 12-23. DOI: 10.3901/JME.2017. 05.012.
[5] GAO Liang, LI Xin-yu, WEN Xiao-yu, LU Chao, WEN Feng. A hybrid algorithm based on a new neighborhood structure evaluation method for job shop scheduling problem [J]. Computers & Industrial Engineering, 2015, 88: 417-429. DOI: 10.1016/j.cie.2015.08.002.
[6] LU Chao, LI Xin-yu, GAO Liang, LIAO Wei, YI Jin. An effective multi-objective discrete virus optimization algorithm for flexible job-shop scheduling problem with controllable processing times [J]. Computers & Industrial Engineering, 2017, 104: 156-174. DOI: 10.1016/j.cie.2016.12.020
[7] ZHANG Su-jun, GU Xing-sheng. An effective discrete artificial bee colony algorithm for flow shop scheduling problem with intermediate buffers [J]. Journal of Central South University, 2015, 22(9): 3471-3484. DOI: 10.1007/ s11771-015-2887-x.
[8] GU Jiu-chun, JIANG Tian-hua, ZHU Hui-qi, ZHANG Chao. Low-carbon job shop scheduling problem with discrete genetic-grey wolf optimization algorithm [J]. Journal of Advanced Manufacturing Systems, 2020, 19(1): 1-14. DOI: 10.1142/S0219686720500018.
[9] ZHENG Xiao-long, WANG Ling. A knowledge-guided fruit fly optimization algorithm for dual resource constrained flexible job-shop scheduling problem [J]. International Journal of Production Research, 2016, 54(18): 5554-5566. DOI: 10.1080/00207543.2016.1170226.
[10] LUAN Fei, CAI Zong-yan, WU Shu-qiang, LIU Shi-Qiang, HE Yi-xin. Optimizing the low-carbon flexible job shop scheduling problem with discrete whale optimization algorithm [J]. Mathematics, 2019, 7(8): 688. DOI: 10.3390/ math7080688.
[11] LU Yi, LU Jia-cheng, JIANG Tian-hua. Energy-conscious scheduling problem in a flexible job shop using a discrete water wave optimization algorithm [J]. IEEE ACCESS, 2019, 7: 101561-101574. DOI: 10.1109/ACCESS.2019. 2930281.
[12] XIAO Hua-jun. Research on dual resource flexible job shop scheduling problem considering energy efficiency [D]. Wuhan: Huazhong University of Science and Technology, 2018. (in Chinese)
[13] LI Jing-yao, HUANG Yuan, WANG Jun-qiang. Scheduling strategy of dual resource constrained job shop based on compressed time window [J]. Computer Integrated Manufacturing Systems, 2016, 22(12): 2827-2835. DOI: 10.13196/j.cims.2016.12.011. (in Chinese)
[14] ZHOU Ya-qing, YANG Chang-qi, LU You-long, JIN Yong-qiao, ZHANG Jie. Scheduling the production of aerospace structural parts with dual resource constraints [J]. Journal of Mechanical Engineering, 2018, 54(9): 55-63. DOI: 10.3901/JME.2018.09.055. (in Chinese)
[15] CHEN Yong, WU Yun-xiang, WANG Ya-liang, LU Jian-xia. Multi-assembly line robust scheduling of double resource constrains under uncertain orders [J]. China Mechanical Engineering, 2014, 25(12): 1567-1573. DOI: 10.3969/j.issn. 1004-132X.2014.12.002. (in Chinese)
[16] ZHANG Jing, WANG Wan-liang, XU Xin-li. A hybrid discrete particle swarm optimization for dual-resource constrained job shop scheduling with resource flexibility [J]. Journal of Intelligent Manufacturing, 2017, 28(8): 1961-1972. DOI: 10.1007/s10845-015-1082-0.
[17] WU Xiu-li, ZHANG Zhi-qiang, ZHAO Ning, LI Jun-qing. Production scheduling and preventive maintenance plan optimization with hyper-heuristics memetic algorithm [J]. Computer Integrated Manufacturing Systems, 2019, 25(8): 1885-1896. DOI: 10.13196/j.cims.2019.08.003. (in Chinese).
[18] LIU Er-hui, YAO Xi-fan, TAO tao, JIN Hong. Improved flower pollinaton algorithm for job shop scheduling problems integrated with AGVs [J]. Computer Integrated Manufacturing Systems, 2019, 25(9): 2219-2236. DOI: 10.13196/j.cims.2019.09.010. (in Chinese)
[19] XU Wen-xiang, GUO Shun-sheng, LI Xi-xing, GUO Chen, WU Rui, PENG Zhao Peng, GUIDA M. A dynamic scheduling method for logistics tasks oriented to intelligent manufacturing workshop [J]. Mathematical Problems in Engineering, 2019: 1-18. DOI: 10.1155/2019/7237459.
[20] FONTS D B M, HOMAYOUNI S M. Joint production and transportation scheduling in flexible manufacturing systems [J]. Journal of Global Optimization, 2019, 74(4): 879-908. DOI: 10.1007/s10898-018-0681-7.
[21] LYU X F, SONG Y C, HE C Z, LEI Q, GUO W F. Approach to integrated scheduling problems considering optimal number of automated guided vehicles and conflict-free routing in flexible manufacturing systems [J]. IEEE ACCESS, 2019, 7: 74909-74924. DOI: 10.1109/ACCESS.2019. 2919109.
[22] LI G M, ZENG B, LIAO W, LI X Y, GAO L. A new AGV scheduling algorithm based on harmony search for material transfer in a real-world manufacturing system [J]. Advances in Mechanical Engineering, 2018, 10(3): 604-616. DOI: 10.1177/ 1687814018765560.
[23] UMAR A U, ARIFFIN M K A, ISMAIL N, TANG S H. Hybrid multiobjective genetic algorithms for integrated dynamic scheduling and routing of jobs and automated-guided vehicle (AGV) in flexible manufacturing systems (FMS) environment [J]. The International Journal of Advanced Manufacturing Technology, 2015, 81(9-12): 2123-2141. DOI: 10.1007/s00170-015-7329-2.
[24] LIU Wei-min. Research on AGV path planning and scheduling system [D]. Guangzhou: South China University of Technology, 2016. (in Chinese)
[25] WANG Jia-rong, LOU Pei-huang, WANG Xiao-yong. Dynamic path planning and scheduling for multiple AGV system based on improved two-stage traffic control scheme [J]. Mechanical Science and Technology for Aerospace Engineering, 2008 (9): 1211-1216. DOI: 10.3321/j.issn:1003-8728.2008.09.023. (in Chinese)
[26] WEN Zheng, SUN Hua-ke. MATLAB intelligent algorithm [M]. Beijing: Tsinghua University Press, 2017: 145-195. (in Chinese)
[27] SUN Xiao-shun. Research on AGV scheduling method in large workshop [D]. Wuhan: Huazhong University of Science and Technology, 2017. (in Chinese).
[28] ZHANG Yan, LI Ling-ling, LIN Hsiung-cheng, MA Ze-wen, ZHAO Jiang. Development of path planning approach using improved A-star algorithm in AGV system [J]. Journal of Internet Technology, 2019, 20(3): 915-924. DOI: 10.3966/ 160792642019052003023.
[29] YU He-nian, BAI Hua, LI Chao. Research and simulation on path planning of warehouse multi-AGV system [J]. Computer Engineering and Applications, 2020, 56(2): 233-241. DOI: 10.3778/j.issn.1002-8331. 1904-0178. (in Chinese)
[30] HE Chang-zheng, SONG Yu-chuan, LEI Qi, LU Xiang-fei, LIU Ruan-xiang, CHEN Jin. Integrated scheduling of multiple AGVs and machines in flexible job shop [J]. China Mechanical Engineerin, 2019, 30(4): 438-447. DOI: 10.3969/ j.issn.1004-132X.2019.04.009. (in Chinese)
(Edited by ZHENG Yu-tong)
中文导读
智能制造车间AGV与机器双资源集成调度问题
摘要:传统车间调度仅考虑单一因素影响下的资源配置的效果,本文研究了智能制造车间环境下AGV与机器的双资源集成调度问题。综合考虑机器、工件和AGV等约束,建立了AGV与机器的双资源集成调度数学模型。确定基于拓扑地图的双向单路径固定式引导系统,定义了AGV运输任务模。采用改进A*路径寻优算法确定最优路径,阐述路径冲突消除机制。利用改进NSGA-Ⅱ算法确定机床的加工工件序列,引入竞争机制进行AGV运输任务分配。通过车间生产实例对所提模型和方法进行验证。结果表明,所提出的基于AGV与机器双资源环境下的集成调度策略是有效的。
关键词:双资源集成调度;改进A*算法;改进NSGA-Ⅱ算法;竞争机制
Foundation item: Project(BK20201162) supported by the General Program of Natural Science Foundation of Jiangsu Province, China; Project(JC2019126) supported by the Science and Technology Plan Fundamental Scientific Research Funding Project of Nantong, China; Project(CE20205045) supported by the Changzhou Science and Technology Support Plan (Social Development), China; Project(51875171) supported by the National Nature Science Foundation of China
Received date: 2020-10-22; Accepted date: 2021-01-19
Corresponding author: YUAN Ming-hai, PhD, Associate Professor; Tel: +86-13861191639; E-mail: ymhai@hhu.edu.cn; ORCID: https:// orcid.org/0000-0003-0204-0260

