J. Cent. South Univ. Technol. (2011) 18: 184-189
DOI: 10.1007/s11771-011-0678-6
Fuzzy entropy design for non convex fuzzy set and application to mutual information
LEE Sang-Hyuk1, LEE Sang-Min1, SOHN Gyo-Yong2, KIM Jaeh-Yung3
1. Department of Electronics Engineering, Inha University, Incheon 402-751, Korea;
2. School of Electrical Engineering and Computer Science, Kyungpook National University,
Daegu 702-701, Korea;
3. School of Mechatronics, Changwon National University, Changwon 641-773, Korea
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: Fuzzy entropy was designed for non convex fuzzy membership function using well known Hamming distance measure. The proposed fuzzy entropy had the same structure as that of convex fuzzy membership case. Design procedure of fuzzy entropy was proposed by considering fuzzy membership through distance measure, and the obtained results contained more flexibility than the general fuzzy membership function. Furthermore, characteristic analyses for non convex function were also illustrated. Analyses on the mutual information were carried out through the proposed fuzzy entropy and similarity measure, which was also dual structure of fuzzy entropy. By the illustrative example, mutual information was discussed.
Key words: fuzzy entropy; non convex fuzzy membership function; distance measure; similarity measure; mutual information
1 Introduction
Characterization and quantification of fuzziness play an important role in data management [1]. Especially, the management of uncertainty affects the system modeling and designing problem [2]. The results about the fuzzy set entropy have been well known by the previous researchers [3-4]. LIU [4] had proposed the axiomatic definitions of entropy, distance measure and similarity measure, and discussed the relations among these three concepts. It also contained the relation between distance measure and fuzzy entropy. PAL and PAL [5] analyzed the classical Shannon information entropy. They also gave a fuzzy information measure for the discrimination of a fuzzy set relative to some other fuzzy sets. Recently, the relation between similarity and dissimilarity was reported [6].
Knowledge in fuzzy set could be obtained through analyzing fuzzy membership function. However, most parts of fuzzy set analysis were emphasized on the convex fuzzy membership function. Thus, non convex fuzzy membership attracted interests. In order to apply fuzzy entropy to non convex fuzzy membership function, understanding the characteristic of fuzzy sets is required first. With previous result of fuzzy entropy, fuzzy entropy for non convex membership function was taken [7]. The fuzzy entropy was already designed based on the distance measure. Entropy value is proportional to the difference area between fuzzy membership function and crisp set. However, fuzzy membership function considered was restricted to convex-type fuzzy membership function. Extension of the fuzzy entropy to non convex membership function has to be done.
In the previous results, it was shown that dissimilarity measure was proportional to fuzzy entropy, and similarity measure was taken into the dual of dissimilarity measure [8]. Hence, designs of similarity and dissimilarity measure were easy if one of the measures was taken. To evaluate or analyze the mutual information between two fuzzy sets, it was also essential to study the data information such as similarity or fuzzy entropy [9]. From the results of DING, mutual information measure was proposed, and the proposed measure was verified through artificial example. The relative information calculation indicated that the evaluation result was almost the same as that of the previous similarity results.
In this work, axiomatic definitions of entropy, previous fuzzy entropy for convex membership function were introduced. Conventional results on the fuzzy entropy and similarity were also shown. With graphical interpretation, differences between convex and non convex fuzzy membership functions were explained, and fuzzy entropy for non convex membership function wasderived. Mutual information using fuzzy entropy and similarity measure was done.
2 Fuzzy entropy
2.1 Preliminary results
Definition 1 [4]: A real function designed as e:F(X)→R+ or e:P(X)→R+ is called an entropy on F(X) or P(X) if e has the following properties:
(E1) e(D)=0, 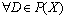
(E2)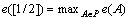
(E3) e(A*)≤e(A), for any sharpening A* of A
(E4) (AC)=e(A), 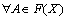
where [1/2] denotes the fuzzy set in which the value of the membership function is 1/2, R+=[0, ∞], X is the universal set, F(X) is the class of all fuzzy sets on X, P(X) is the class of all crisp sets on X and DC is the complement of D. A lot of fuzzy entropy satisfying Definition 1 can be formulated. Now, two fuzzy entropies are illustrated without proofs [7].
If distance d satisfies d(A, B)=d(AC, BC), A, B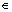 F(X), then
F(X), then
e(A)=2d((A Anear), [1]X)+2d((A
Anear), [1]X)+2d((A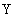 Anear), [0]X)-2 (1)
Anear), [0]X)-2 (1)
and
e(A)=2d((A Afar), [0]X)+2d((A
Afar), [0]X)+2d((A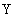 Afar), [1]X) (2)
Afar), [1]X) (2)
where fuzzy entropies satisfy Definition 1.
The exact meaning of fuzzy entropy of fuzzy set A is fuzziness of fuzzy set A with respect to crisp set. Crisp set is commonly considered Anear or Afar [4]. In the above fuzzy entropies, one of well-known Hamming distances is commonly used as the distance measure between fuzzy sets, A and B:
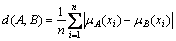
where X={x1, x2, …, xn}, |k| denotes the absolute value of k. μA(x) is used as the membership function of A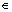 F(X). Fuzzy entropy (Eqs.(1) and (2)) satisfies Definition 1. From Definition 1, fuzzy entropy of non convex fuzzy set can be formulated even considering that the fuzzy set satisfies non convex fuzzy membership function. Fuzzy entropy and similarity measure can also be explained from graphical point of view. Fuzzy entropy indicates the degree of uncertainty or the dissimilarity between two data sets, fuzzy set and corresponding ordinary set generally. Hence, it can be designed through many ways satisfying Definition 1. However, similarity measure is used to evaluate the degree of similarity between all kinds of data sets.
F(X). Fuzzy entropy (Eqs.(1) and (2)) satisfies Definition 1. From Definition 1, fuzzy entropy of non convex fuzzy set can be formulated even considering that the fuzzy set satisfies non convex fuzzy membership function. Fuzzy entropy and similarity measure can also be explained from graphical point of view. Fuzzy entropy indicates the degree of uncertainty or the dissimilarity between two data sets, fuzzy set and corresponding ordinary set generally. Hence, it can be designed through many ways satisfying Definition 1. However, similarity measure is used to evaluate the degree of similarity between all kinds of data sets.
Next, fuzzy entropy and similarity measure are explained by the graphical illustration in Fig.1. From Fig.1, the shaded area represents the common information of two fuzzy sets with membership functions. Hence, regions C and D satisfy the definition of similarity measure. Outside regions of C and D denote the dissimilarity between two data sets [8].
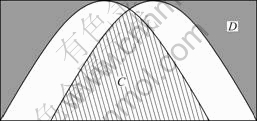
Fig.1 Gaussian type two membership functions
Total information between fuzzy sets C and D satisfies the following relation naturally. From s+d=1, D is the dissimilarity measure, and it is illustrated by the following result:
D(A, B)=d(A, A B)+d(B, A
B)+d(B, A B)=1-s(A, B)
B)=1-s(A, B)
Therefore, similarity measure
s=1-d(A, A B)-d(B, A
B)-d(B, A B)
B)
is satisfied by s=1-d.
The relation between similarity measure and dissimilarity measure can be derived as
D(A, B)+s(A, B)=1 (3)
By the comparison of Eq.(3) with Fig.1, it is clear that s(A, B) is represented by graphical summation of C and D.
Here, the total information of two fuzzy set membership functions is represented by the summation of similarity and dissimilarity measure. Next, non convex fuzzy membership function is introduced [10]. Non convex fuzzy sets are not common fuzzy membership function.
2.2 Non convex membership function
From Ref.[10], it is known that the definition of convexity of a fuzzy set is not as strict as the common definition of convexity of a function. The definition of convexity is presented.
Definition 2 [9]: A fuzzy set A is convex if and only if for any x1, x2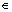 X and any λ
X and any λ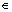 [0, 1],
[0, 1],
μA(λx1+(1-λ)x2)≥min(μA(x1), μA(x2)) (4)
Non convexity fuzzy set is said if it is not convex. Non convex membership functions can be notified naturally as three sub classes [10]:
1) Elementary non convex membership functions,
2) Time related non convex membership functions, and
3) Consequent non convex membership functions.
First, a discrete fuzzy set is expressed by elementary non convex fuzzy membership functions. However, continuous domain non convex fuzzy set may be less common. Next, time related non convex membership functions can be found in energy supply by time of day or year, mealtime by time of day. This fuzzy set is interesting as it is also sub-normal and never has a membership of zero. Finally, Mamdani fuzzy inference is a typical example of consequent non convex sets. In a rule based fuzzy system, the result of Mamdani fuzzy inference is a non convex fuzzy set where the antecedent and consequent fuzzy sets are triangular and/or trapezoidal.
JANG et al [9] insisted that the definition of convexity of a fuzzy set was not as strict as the common definition of convexity of a function. Then, the mathematical definition of convexity of a function is
f(λx1+(1-λ)x2)≥λf(x1)+(1-λ)f(x2) (5)
which is a tighter condition than Eq.(4).
Fig.2(a) shows two convex fuzzy sets with the left fuzzy set satisfying both Eq.(4) and Eq.(5) while the right one satisfying Eq.(4) only. Whereas Fig.2(b) shows definitely a non convex fuzzy set.
By the definition of JANG et al, fuzzy entropy of

Fig.2 Convex membership function and non convex membership function [8]: (a) Two convex fuzzy sets; (b) One non convex fuzzy set
Fig.2(a) is satisfied. However, if two fuzzy sets are considered one fuzzy set, then it has to be considered totally as non convex fuzzy set. Hence, by the computation of Eq.(1), the fuzzy entropy value can be obtained. Fig.2(b) shows the typical non convex membership function. If the crisp set is applied as rectangular, the computation of fuzzy entropy can be possible with fuzzy entropy measure. Non convex fuzzy sets are uncommon in actual circumstance, and example is not easy to consider. However, for the design of general fuzzy entropy, it has to be solved for non convex fuzzy membership case.
3 Fuzzy entropy of non convex membership function
Non convex fuzzy membership function is usually uncommon. However, drinking milk temperature is proper as the non convex fuzzy membership function. Medium temperature is not popular to drink. Fig.3 shows the preference temperature of drinking milk.
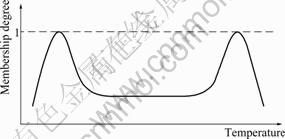
Fig.3 Preference temperature of drinking milk
As shown in Fig.3, the calculation of uncertainty for the non convex fuzzy membership function needs more consideration such as the definition of certain facts, because there are multiple certain facts or numerical values. Now, the non convex membership function is focused on. First, the definition of fuzzy entropy is considered. Conditions of (E1) and (E2) are also natural for non convex membership function too. However, (E3) and (E4) are important to decide the structure of fuzzy entropy. For fuzzy membership function, crisp set corresponding to fuzzy set is assigned as follows.
For every non convex fuzzy set A, let crisp set be Anear. Then, two fuzzy entropy measures (Eqs.(1) and (2)) are applicable to non convex fuzzy membership function. It can be shown that two fuzzy entropies (Eqs.(1) and (2)) are satisfied as fuzzy entropy and non convex fuzzy membership function [6-7]. It is essential to assign the crisp set Anear of fuzzy set A. Crisp set Anear of fuzzy set A is also non convex. Finally, (E4) is also satisfied if the same Anear is used. Next, two fuzzy entropy measures are presented as fuzzy entropy of non convex membership function.
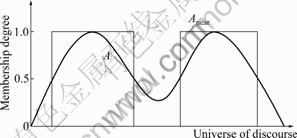
Fig.4 Fuzzy set and corresponding crisp set
Theorem 1: If distance d satisfies d(A, B)=d(AC, BC) and for convex or non convex A, B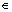 F(X),
F(X),
e(A)=2d((A Anear), [1]X)+2d((A
Anear), [1]X)+2d((A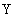 Anear), [0]X)-2
Anear), [0]X)-2
is the fuzzy entropy.
Proof: For (E1), 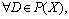 Dnear=D, therefore,
Dnear=D, therefore,
e(D)=2d((D Dnear), [1]X)+2d((D
Dnear), [1]X)+2d((D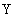 Dnear), [0]X)-2=
Dnear), [0]X)-2=
2d(D, [1]X)+2d(D, [0]X)-2=0
(E2) represents that crisp set 1/2 has the maximum entropy. Therefore, the entropy e[1/2] satisfies
e([1/2])=2d(([1/2] [1/2]near), [1]X)+2d(([1/2]
[1/2]near), [1]X)+2d(([1/2]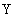 [1/2]near), [0]X)-2=2d([1/2], [1]X)+2d([1/2], [0]X)-2=1
[1/2]near), [0]X)-2=2d([1/2], [1]X)+2d([1/2], [0]X)-2=1
In the above equation, [1/2]near=[1] is satisfied.
(E3) shows that the entropy of the sharpened version of fuzzy set A is less than or equal to e(A). For the proof, A*near=Anear is also used:
e(A*)=2d((A* A*near), [1]X)+2d((A*
A*near), [1]X)+2d((A*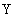 A*near), [0]X)-2≤2d((A
A*near), [0]X)-2≤2d((A Anear), [1]X)+2d((A
Anear), [1]X)+2d((A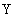 Anear), [0]X)-2=e(A)
Anear), [0]X)-2=e(A)
The inequality is obvious because ((A* A*near), [0]X)≤d((A
A*near), [0]X)≤d((A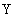 Anear), [0]X). Finally, (E4) is proved using the assumption d(A, B)=d(AC, BC). Hence, it is also obvious that
Anear), [0]X). Finally, (E4) is proved using the assumption d(A, B)=d(AC, BC). Hence, it is also obvious that
e(A)=2d((A Anear), [1]X)+2d((A
Anear), [1]X)+2d((A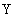 Anear), [0]X)-2=2d((AC
Anear), [0]X)-2=2d((AC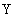 ACnear), [0]X)+2d((AC
ACnear), [0]X)+2d((AC ACnear), [1]X)-2=e(AC)
ACnear), [1]X)-2=e(AC)
Dual fuzzy entropy for Anear can be derived as the following theorem. Its corresponding crisp set is used as the complement set of Anear.
Theorem 2: If distance d satisfies d(A, B)=d(AC, BC) and for convex or non convex A, B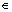 F(X),
F(X),
e(A)=2d((A Afar), [0]X)+2d((A
Afar), [0]X)+2d((A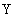 Afar), [1]X)
Afar), [1]X)
is also the fuzzy entropy.
Proof is similar to that of Theorem 1. For non convex fuzzy set, it is also applicable to the convex fuzzy entropy computation. However, proper assignment of crisp set is required to formulate fuzzy entropy measure. Entropy application to mutual information is introduced.
4 Application to mutual information
Fuzzy entropy has been applied to various fields such as clustering, pattern recognition, or other areas. Especially, the fuzzy relative information has been analyzed through fuzzy entropy [11]. Fuzzy entropy is explained by comparing fuzzy set with respect to the corresponding ordinary set. In order to organize the relative information measure, virtual ordinary set has to be ready for the entropy calculation. However, the similarity measure can provide direct calculation between two fuzzy membership functions. Hence, the relative information measure design with similarity measure can be efficient to minimize the calculation time and decrease the design complexity. The definition of relative information has not been formulated by researchers. In Ref.[11], they just proposed fuzzy relative information measure R[A, B] as the fuzzy relative information measure of B to A. Hence, the definition of fuzzy relative information measure will be presented through analyzing the definition of R[A, B].
Proposition 1: Fuzzy relative information measure R[A, B] satisfies the following properties:
1) R[A, B]=0 if and only if there is no intersection between A and B, or ordinary sets.
2) R[A, B]=R[B, A] if and only if H[A]=H[B].
3) R[A, B] takes the maximum value and R[A, B]≥R[B, A] if and only if A is contained in B, i.e, μA(x)≤μB(x) for 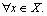
4) If 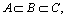 then R[B, A]≥R[C, A] and R[A, B]=R[A, C]=R[B, C].
then R[B, A]≥R[C, A] and R[A, B]=R[A, C]=R[B, C].
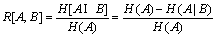 (6)
(6)
is represented by an influence degree of the fuzzy set A to the fuzzy set B. H[A] represents the entropy function based on the Shannon function:
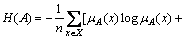
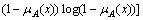
and
H(A∩B)=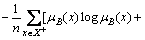
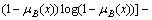
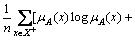
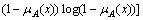
where X+={x|x X, μA(x)≥μB(x)} and X-={x|x
X, μA(x)≥μB(x)} and X-={x|x X, μA(x)< μB(x)} are satisfied, respectively. R[A, B] satisfies the ratio between entropies of A
X, μA(x)< μB(x)} are satisfied, respectively. R[A, B] satisfies the ratio between entropies of A B and A. Hence, virtual ordinary set corresponding to the fuzzy set has to be needed [12]. LIU [4] insisted that entropy can be calculated from the similarity measure and dissimilarity measure, which is denoted by s+d=1. With this concept, relative information measure can be designed via similarity measure. By the definition of entropy for a certain fact, H(A
B and A. Hence, virtual ordinary set corresponding to the fuzzy set has to be needed [12]. LIU [4] insisted that entropy can be calculated from the similarity measure and dissimilarity measure, which is denoted by s+d=1. With this concept, relative information measure can be designed via similarity measure. By the definition of entropy for a certain fact, H(A B) and H[A] satisfy H((A
B) and H[A] satisfy H((A B), (A
B), (A B)near) and H(A, Anear), respectively. Here, (A
B)near) and H(A, Anear), respectively. Here, (A B)near satisfies the same definition of Anear. Roughly, it can be satisfied:
B)near satisfies the same definition of Anear. Roughly, it can be satisfied:
 (7)
(7)
where s((A B), (A
B), (A B)near)=1-H((A
B)near)=1-H((A B), (A
B), (A B)near) and s(A, Anear)=1-H(A, Anear).
B)near) and s(A, Anear)=1-H(A, Anear).
This measure also satisfies Proposition 1. Next, another relative information measure satisfying Proposition 1 without virtual ordinary sets (A B)near and Anear is considered. Fuzzy relative information characteristic satisfying Proposition 1 is proposed through entropy of fuzzy set A and B, R[A, B]. Under the consideration of the structure of similarity measure, the relative information measure satisfies the following formation:
B)near and Anear is considered. Fuzzy relative information characteristic satisfying Proposition 1 is proposed through entropy of fuzzy set A and B, R[A, B]. Under the consideration of the structure of similarity measure, the relative information measure satisfies the following formation:
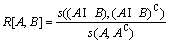 (8)
(8)
By considering the characteristics of Proposition 1, properties of (1) and (2) are clear. Property (3) is also satisfied because A B=A if μA(x)≤μB(x). Furthermore, R[A, B]=1 and R[A, B]≤1 are satisfied naturally. Finally, property (4) is followed with the fact of property (5). In proposed Eq.(8), similarity measure can be replaced.
B=A if μA(x)≤μB(x). Furthermore, R[A, B]=1 and R[A, B]≤1 are satisfied naturally. Finally, property (4) is followed with the fact of property (5). In proposed Eq.(8), similarity measure can be replaced.
Consider the reliable data selection problem in Ref.[7]. This example is also considered as the kind of pattern recognition [13-15]. For proposed relative information measure (Eq.(6)), denominator is the same for all trials. Hence, numerator comparisons are followed. In s((A B), (A
B), (A B)C), set A is considered the middle level fuzzy set, and its membership values are satisfied when sample values are included from 37 to 71. Whereas, test data are also considered by fuzzy set B, and its membership values are satisfied in Table 1. Table 1 illustrates the information of fuzzy set B and its operation with crisp set A.
B)C), set A is considered the middle level fuzzy set, and its membership values are satisfied when sample values are included from 37 to 71. Whereas, test data are also considered by fuzzy set B, and its membership values are satisfied in Table 1. Table 1 illustrates the information of fuzzy set B and its operation with crisp set A.
Computation of s((A B), (A
B), (A B)C) is followed by the entropy measure.
B)C) is followed by the entropy measure.
Values in Table 2 indicate the influence degree of the fuzzy set A to fuzzy set B, i.e, the influence degree of the middle level set to selection data. Hence, if the value goes to zero, selection is similar to the considered set. Actually, Test 2 is very similar to the middle level fuzzy set.
Table 1 Computation of A∩B and (A∩B)C
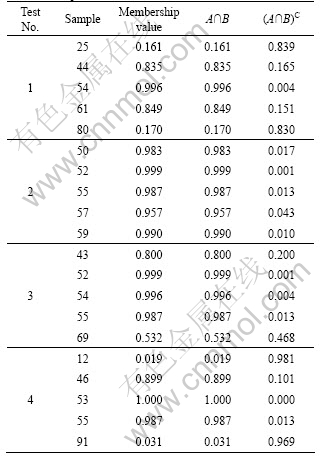
Table 2 Similarity computation

5 Conclusions
1) Fuzzy entropy of non convex fuzzy membership function is designed. To understand the property of non convex fuzzy membership function, graphical explanation is introduced, and its property is discussed. Relation between fuzzy entropy and similarity measure is also explained through graphical description.
2) Previous fuzzy entropy measure for fuzzy set is extendable to non convex fuzzy membership function. To construct entropy for non convex fuzzy set, it is essential to assign corresponding crisp set, that is, multiple corresponding crisp set is also non convex set.
3) To construct the mutual information measure, fuzzy entropy or similarity measure should be formulated. Generalized fuzzy entropy can be converted into the similarity measure, and mutual information measure is formulated to evaluate the influence degree of the middle level set to selection data. Finally, calculation is carried out through similarity measure.
References
[1] BHANDARI D, PAL N R. Some new information measure of fuzzy sets [J]. Information Science, 1993, 67: 209-228.
[2] GHOSH A. Use of fuzziness measure in layered networks for object extraction: A generalization [J]. Fuzzy Sets and Systems, 1995, 72: 331-348.
[3] KOSKO B. Neural networks and fuzzy systems [M]. Englewood Cliffs, NJ: Prentice-Hall, 1992: 275-278.
[4] LIU Xue-cheng. Entropy, distance measure and similarity measure of fuzzy sets and their relations [J]. Fuzzy Sets and Systems, 1992, 52: 305-318.
[5] PAL N R, PAL S K. Object-background segmentation using new definitions of entropy [J]. IEEE Proceeding, 1989, 36: 284-295.
[6] LEE S H, PEDRYCZ W, SOHN G Y.Design of similarity and dissimilarity measures for fuzzy sets on the basis of distance measure [J]. International Journal of Fuzzy Systems, 2009, 11(2): 67-72.
[7] LEE S H, CHEON S P, KIM Jinho. Measure of certainty with fuzzy entropy function [J]. Lecture Notes in Artificial Intelligence, 2006, 4114: 134-139.
[8] LEE S H, RYU K H, SOHN G Y. Study on entropy and similarity measure for fuzzy set [J]. IEICE Trans Inf & Syst, 2009, E92/D(9): 1783-1786.
[9] DING S F, XIA S H, JIN F X, SHIS Z Z. Novel fuzzy information proximity measures [J]. Journal of Information Science, 2007, 33(6): 678-685.
[10] JANG J S R, SUN C T, MIZUTANI E. Neuro-fuzzy and soft computing [M]. Upper Saddle River, Prentice Hall, 1997: 19-21.
[11] GARIBALDI J M, MUSIKASUWAN S, OZEN T, JOHN R I. A case study to illustrate the use of non convex membership functions for linguistic terms [C]// 2004 IEEE International Conference onFuzzy Systems. Budapest, Hungary, 2004: 1403-1408.
[12] R?BILL? Y. Decision making over necessity measures through the Choquet integral criterion [J]. Fuzzy Sets and Systems, 2006, 157(23): 3025-3039.
[13] SUGUMARAN V, SABAREESH G R, RAMACHANDRAN K I. Fault diagnostics of roller bearing using kernel based neighborhood score multi-class support vector machine [J]. Expert Systems with Applications, 2008, 34(4): 3090-3098.
[14] KANG W S, CHOI J Y. Domain density description for multiclass pattern classification with reduced computational load [J]. Pattern Recognition, 2009, 41(6): 1997-2009.
[15] SHIH F Y, ZHANG K. A distance-based separator representation for pattern classification [J]. Image and Vision Computing, 2008, 26(5): 667-672.
(Edited by YANG Bing)
Foundation item: Work supported by the Second Stage of Brain Korea 21 Projects; Work(2010-0020163) supported by the Priority Research Centers Program through the National Research Foundation (NRF) funded by the Ministry of Education, Science and Technology of Korea
Received date: 2010-03-28; Accepted date: 2010-06-24
Corresponding author: LEE Sang-Hyuk, Professor, PhD; Tel: +82-55-213-3884; E-mail: leehyuk@inha.ac.kr