简介概要

Bi-2223带材在自场和外场条件下电流密度分布的数值分析

来源期刊：稀有金属2014年第5期

论文作者：王磊王秋良王晖

文章页码：755 - 761

关键词：Bi-2223带材;横向磁场;传导电流;电流密度分布;

摘要：Bi-2223超导带材是一种具有较高载流能力的高温超导材料,被广泛用来制造高场强的内插磁体以及核磁共振（NMR）,磁头振成象（MRI）等核磁共振设备。在超导磁体的设计以及交流损耗的计算中,不可避免地会涉及到Bi-2223带材中电流密度的分布。基于Brandt数值分析的方法,考虑了自场和外场对于临界电流密度的影响,利用Matlab对Bi-2223带材截面的电流密度分布进行了计算。为了便于仿真计算,用实验测得的临界电流与磁场关系的数据代替了Kim模型和Bean模型。在计算中主要施加了3种外加条件:（1）只施加横向磁场;（2）只通入传导电流;（3）将通入传导电流的带材放置于背景场中。结果显示,当Im<20 A或者Bm<100 mT时,Bi-2223带材中电流密度随着传导电流和外场的幅值增加而增长;当Im>20 A或者Bm>100 mT时,Bi-2223带材中电流密度的最大值随着传导电流和外场的幅值增加而减小;屏蔽电流会随着外磁场的频率增加而减小,传导电流的频率对于电流分布的影响可以忽略不计;当通入传导电流的Bi-2223带材放置于背景场中时,电流密度的分布相对于中心不再对称,并且饱和电流值会随着外磁场的幅值增加而减小。

网络首发时间: 2013-12-27 14:36

稀有金属 2014,38(05),755-761 DOI:10.13373/j.cnki.cjrm.2014.05.003

Bi-2223带材在自场和外场条件下电流密度分布的数值分析

王磊王秋良王晖

中国科学院电工研究所应用超导重点实验室

中国科学院大学

摘要：

Bi-2223超导带材是一种具有较高载流能力的高温超导材料, 被广泛用来制造高场强的内插磁体以及核磁共振 (NMR) , 磁头振成象 (MRI) 等核磁共振设备。在超导磁体的设计以及交流损耗的计算中, 不可避免地会涉及到Bi-2223带材中电流密度的分布。基于Brandt数值分析的方法, 考虑了自场和外场对于临界电流密度的影响, 利用Matlab对Bi-2223带材截面的电流密度分布进行了计算。为了便于仿真计算, 用实验测得的临界电流与磁场关系的数据代替了Kim模型和Bean模型。在计算中主要施加了3种外加条件: (1) 只施加横向磁场; (2) 只通入传导电流; (3) 将通入传导电流的带材放置于背景场中。结果显示, 当Im<20 A或者Bm<100 mT时, Bi-2223带材中电流密度随着传导电流和外场的幅值增加而增长;当Im>20 A或者Bm>100 mT时, Bi-2223带材中电流密度的最大值随着传导电流和外场的幅值增加而减小;屏蔽电流会随着外磁场的频率增加而减小, 传导电流的频率对于电流分布的影响可以忽略不计;当通入传导电流的Bi-2223带材放置于背景场中时, 电流密度的分布相对于中心不再对称, 并且饱和电流值会随着外磁场的幅值增加而减小。

关键词：

Bi-2223带材;横向磁场;传导电流;电流密度分布;

中图分类号： TM26

作者简介：王磊 (1988-) , 男, 河北人, 博士研究生, 研究方向:高温超导磁体的设计及优化;E-mail:wanglei@mail.iee.ac.cn;;王秋良, 研究员;电话:010-82547162;E-mail:qiuliang@mail.iee.ac.cn;

收稿日期：2013-09-04

基金：国家自然科学基金项目 (50925726) 资助;

Numerical Analysis of Current Density Distributions in Bi-2223 Tapes under Self and External Fields

Wang Lei Wang Qiuliang Wang Hui

Key Laboratory of Applied Superconductivity, Institute of Electrical Engineering, Chinese Academy of Sciences

University of Chinese Academy of Sciences

Abstract：

Bi-2223 was a kind of significant superconductor material with high current carrying capability, it was commonly applied in fields such as high temperature superconducting magnet, nuclear magnetic resonance spectrometer ( NMR) , magnetic resonance imaging ( MRI) , and other equipments. The design of superconducting magnet and the AC loss calculation were relevant to the distributions of current density and magnetic field in the conductor. The current and magnetic field distributions in Bi-2223 conductors based on Brandt's method through the Matlab was calculated, including the effects of self and external field. For the convenience of calculation, the perpendicular and parallel field dependence of critical current obtained by experiment substituted for Kim-type or Bean model Jc ( B) dependence. Three conditions were applied: ( 1) external magnetic field only, ( 2) transport current only, ( 3) transport current together with external magnetic field. The results showed that when the amplitude of transport current Im< 20 A or applied magnetic field Bm< 100 mT, Jz ( x) increased with the increase of transport current and applied magnetic field. When Im> 20 A or Bm> 100 mT, the max value of Jz ( x) declined with the increase of amplitude of transport current and applied magnetic field. The screening current density decreased with the increase of frequency, but the distribution of Jz ( x) was not so much relevant to the Iafrequency. If the transport current was ramped into a Bi-2223 tape with the background magnetic field, the current density would not be symmetric to the conductor center and the saturated current density would decrease with the increase of Bm.

Keyword：

Bi-2223 tape; transverse field; transport current; current density distribution;

Received： 2013-09-04

Bi-2223材料是一种重要的高温超导材料, 相对于传统的低温超导线材来说, 它的载流能力超过了10 k A·cm^-2 (77 K, 自场) 。随着超导磁体用来制造nuclear magnetic resonance (NMR) 、magnetic resonance imaging (MRI) 等核磁共振设备越来越普遍, 性能优于低温超导材料的Bi-2223带材的应用显得尤为重要。Bi-2223带材中电流密度的分布决定了磁体中交流损耗和电磁力的计算, 在大部分磁体设计过程中, 都会近似地认为电流密度在带材截面中均匀分布, 显然对于高均匀度磁体来说, 这会带来一定的误差。因此获得精确的电流密度分布对于磁体的设计制造来说是至关重要的。

近些年来, 有很多科研机构展开了这方面的研究, Brandt^[1,2]提出了一种基于泊松方程的二维模型计算矩形截面中电流密度的分布。Yazawa等^[3]为了计算Bi-2223/Ag带材中的交流损耗, 在Brandt模型基础之上提出了一种离散化的计算模型。Koyama等^[4]和Yanagisawa等^[5]分别计算了在外加磁场条件下Bi-2223带材中屏蔽电流的分布情况。

临界电流密度对于磁场的依赖关系是超导体的一个重要特性。在大部分文献中, 这种依赖关系主要体现为3种情况: (1) 如果将Bi-2223带材放置于一个背景场中, 带材的临界电流密度主要与外场的大小和方向有关系^[6,7]; (2) 如果将Bi-2223带材中通入一个传导电流, 为了计算的方便, 此时认为带材的临界电流密度是一个常数值^[8]; (3) 如果将通入传导电流的带材放置于一个背景场中, 带材的临界电流密度主要与背景场的大小和方向有关系^[8,9];然而, 传导电流或者屏蔽电流引起的感应磁场 (自场) 也会对带材的临界电流密度产生影响, 当背景场足够小或者传导电流足够大时, 感应磁场的影响就会超过背景场的影响, 从而带材中的电流密度就会重新分布。很显然, 如果忽略感应磁场 (自场) 的影响, 计算结果在一定程度就会产生误差。Brojeny等^[10]在计算中考虑了自场对于带材平均电流密度的影响, 但是他们只计算了带材中静态的电流密度和磁场的分布情况。Brandt^{[11,12,13,14,15]}计算了带材中动态的电流密度分布, 但是忽略了自场的影响。

本文讨论了带材中动态的电流密度的分布情况, 同时考虑了自场和外场对于临界电流密度的影响。在计算中, 分别施加了3种外加条件: (1) 只施加垂直背景场; (2) 只通入传导电流; (3) 将通入传导电流的带材放置于垂直背景场中。同时, 本文讨论了垂直外场和传导电流的幅值和频率对于电流密度以及磁场分布的影响。

1 计算模型

为了简化计算过程, 这里将Bi-2223带材的椭圆截面等效为2a×2b等截面积的矩形, 如图1所示。将带材的截面布置于x-y平面, 2a为带材的宽度, 2b为带材的厚度, 带材在z向的长度认为是无限长。由于Bi-2223带材的宽厚比大于10, 在计算中只考虑z方向上的电流, 背景场的方向平行于y轴。表1列出了计算采用的Bi-2223带材的性能参数。

图1 数值计算模型Fig.1 Numerical simulation model of Bi-2223

表1 Bi-2223带材性能参数Table 1 Parameters of Bi-2223 conductor 下载原图

表1 Bi-2223带材性能参数Table 1 Parameters of Bi-2223 conductor

2 理论推导

本文的理论计算基于Brandt^{[12,13,14,15]}和Yazawa等^[3]的方法, 在计算过程中考虑了自场的影响。在忽略位移电流的情况下, 由麦克斯韦方程组和库伦规范可以得到矢量磁位的方程:

其中, μ₀是真空磁导率, 是z方向的电流密度, 是由z方向的电流产生的矢量磁位。在本文中, 矢量磁位A^→主要由两个部分组成: (1) 由z方向的电流产生的矢量磁位A_J, (2) 由y方向的外磁场产生的矢量磁位A_α。在z方向上, A_α=-x B_α, 因此可以解得A_J为:

因此, 将式 (2) 带入式 (1) 可以得到:

由于只考虑z方向上的矢量磁位, 由式 (3) 可以解得

其中s是x-y截面的面积, 为场点坐标, 为源点坐标, 为积分核。

通过对式 (4) 逆运算可以得到J (r^→) 的表达式为:

分别将式 (5) 的左右两侧对时间求导, 可以得到:

对于Bi-2223带材而言, 电压随电流变化的曲线是非线性的, 一般满足式 (7) 的幂指数关系

其中, J_c是Bi-2223带材的临界电流密度, E_c为规定的临界电流测量标准, 即1.0×10^-4V·m^-1。

将式 (7) 和动态标量位的函数带入到式 (6) 中, 可以得到

其中, 为标量梯度位。在计算中, 将Bi-2223带材在宽度方向上离散化为N个等间距的点, 由于宽厚比的值比较大, 在厚度方向上不再离散化, 因此第i个点的坐标为。因此, 将式 (8) 离散化后可以得到截面上每一个点的电流密度, 即

其中Q_ij是N×N的矩阵, Q_ij^-1是Q_ij的逆矩阵。考虑到当i=j时会在Q_ij矩阵的对角线位置出现奇异点。为了消除奇异点的影响, 在Q_ij的表达式中加入一个因子ε, 即 , 其中

Bi-2223带材的临界电流I_c与垂直场和平行场的关系如图2所示^{[16,17,18,19]}。截面上的电流在第i个点产生的垂直场 (y方向) 和平行场 (x方向) 可以由式 (10) 计算得到^[3]:

其中, R_ij是源点和场点的距离, θ_ij是与x轴正向的夹角。Bi-2223带材截面上流过的电流可以用各点电流密度之和的形式表达, 即

因此, 当时间t=0时, J_i (0) =0;通过迭代式 (9) , (10) , (11) 和图2所示的临界电流和磁场的关系, 在每一个时间点t可以解出N个点的J_i (t) 和一个。计算中用到的I_c0, J_c0, n分别为120 A, 12k A·cm^-2, 21。

图2 归一化电流与垂直场和平行场的关系 (77 K, 自场) Fig.2 Dependance of normalized critical current on perpendic-ular and parallel magnetic field at 77 K

3 结果与讨论

3.1 只施加背景场

在本文的计算中认为y轴方向的外磁场在空间均匀分布, 为正弦磁场B_α=B_msin (ωt+φ) 。外磁场B_α在带材中感应出屏蔽电流, 屏蔽电流会感应出二次场B_i。B_α和B_i同时决定了带材的临界电流密度J_c, 因此会对带材中的电流分布产生影响。

外磁场的频率和相位分别为50 Hz和0, 当幅值由50-100-150-250 m T变化时, 带材中的屏蔽电流密度分布如图3所示。在本文所有的计算中, 如无特殊提及, 所有的结果时间点均取自磁场或者传导电流的四分之一周期处。

由图3 (a) 可以得到, 当外磁场小于100 m T时, 屏蔽电流随着外磁场的增加而增大, 但是当外磁场超过100 m T时, 屏蔽电流的最大值随着外磁场的增加而下降, 如图3 (b) 所示。分析原因为, 当外磁场由0到100 m T变化时, 屏蔽电流密度的最大值小于临界电流密度, 所以屏蔽电流值随着外磁场而增加。当外磁场的值大于100 m T时, Bi-2223带材边缘点的屏蔽电流密度达到了临界电流密度, 由图2可知, 随着垂直磁场的增加, Bi-2223带材的临界电流快速下降。带材中的屏蔽电流会感应出一个磁场, 在边缘处最大, 因此屏蔽电流的最大值会在带材的边缘处出现下降的趋势, 导致了屏蔽电流的最大值随着外磁场的增加而下降。

图3 Bi-2223整体截面屏蔽电流分布 (a) 和Bi-2223边缘电流密度分布 (b) Fig.3Distributions of current density over cross-section (a) and in edge (b) of Bi-2223 conductor

当外磁场的幅值为100 m T时, 频率由35-100-200 Hz变化, 带材中的屏蔽电流分布如图4所示。计算结果显示, 屏蔽电流随着磁场的频率增加而下降。

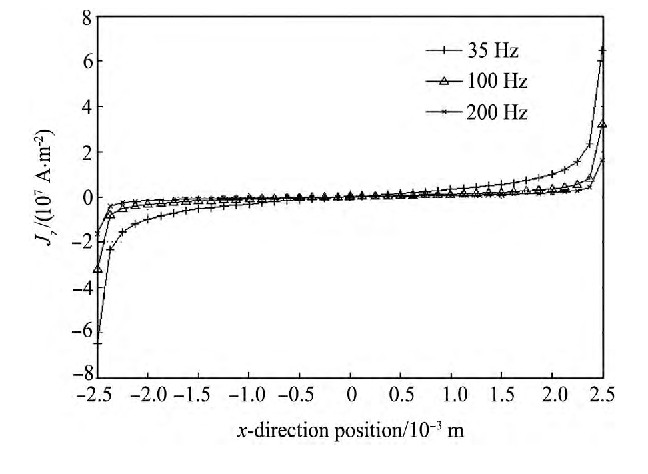
图4 不同磁场频率下Bi-2223截面屏蔽电流分布Fig.4Distributions of screening current density under differ-ent magnetic frequencies

3.2 只通入传导电流

当在Bi-2223带材中通入交变传导电流时, 会在周围空间产生一个交变的磁场。该磁场会导致带材的临界电流下降, 从而影响带材中的电流密度分布。

在计算中, 通入的传导电流为正弦电流I=I_msin (ωt+φ) 。当传导电流的频率和相位分别为50Hz和0, 幅值由10-20-40-60-80 A变化时, 带材中的电流密度分布如图5所示。结果显示, 当通入传导电流时, 带材的边缘先出现电流密度饱和的部分, 随着传导电流幅值的增加, 带材中电流饱和部分逐步向中心扩散, 直到整个带材截面完全饱和。当传导电流的幅值小于20 A时, 电流密度的最大值随着传导电流的幅值增加而增长, 当传导电流的幅值超过20 A时, 电流密度的最大值会随着传导电流的幅值增大而减小。分析原因为, 当传导电流的幅值增加时, 其感应的磁场也会随之增大, 带材的临界电流会随之下降。因此, 随着传导电流幅值的增加, 临界电流会不断下降, 因而导致带材截面中电流密度最大值出现下降的情况。

图5 Bi-2223整体截面屏蔽电流分布 (a) 和Bi-2223边缘电流密度分布 (b) Fig.5Distributions of current density over cross-section (a) and in edge (b) of Bi-2223 conductor

当传导电流的幅值为60 A, 频率由50-100-200 Hz变化时, 电流密度分布如图6所示。结果显示, 虽然传导电流的频率会对电流分布产生一定的影响, 但是这种影响可以忽略不计。

3.3 通入传导电流并置于背景场

当把通入传导电流的Bi-2223带材放置于背景场中时, 带材中的电流密度分布会同时受到自场和外场的影响。在计算中, 传导电流和外场的频率以及相位相等, 分别为50 Hz和0。传导电流和外场的幅值为4种组合方式: (1) 40 A, 60 m T; (2) 60 A, 30 m T; (3) 60 A, 60 m T; (4) 60 A, 100 m T。

图7 (a) 显示了带材截面中电流密度关于中心不再对称, 电流密度的最大值会随着磁场幅值的增加而减小。同时在带材的两个边缘的电流最大值出现差异。分析原因为, 如图7 (b) 所示, 在带材的两个边缘磁场值不同, 导致了两个边缘的临界电流密度不一致, 从而电流密度的最大值也不相同。带材截面电流密度分布图中凹点位置偏离中心的方向与传导电流和外磁场的方向有关。

图6 不同电流频率下Bi-2223带材截面电流分布Fig.6 Current density distributions of Bi-2223 under different current frequencies

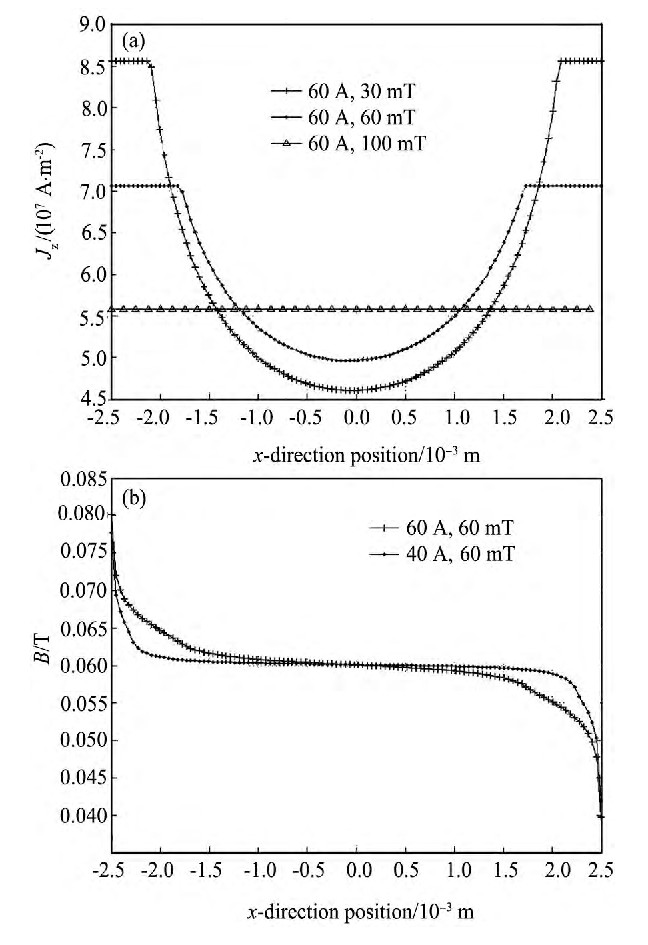
图7 Bi-2223带材截面电流分布图 (a) 和Bi-2223带材截面磁场分布图 (b) Fig.7 Current density distribution (a) and magnetic field dis-tribution (b) of Bi-2223 over cross-section

4 结论

采用数值法计算了Bi-2223带材中电流密度和磁场的分布。在计算中, 考虑了自场对临界电流密度的影响, 同时用实验测得的临界电流与磁场关系数据代替了Kim模型和Bean模型, 简化了计算程序。结果显示, 当I_m<20 A或者B_m<100 m T时, Bi-2223带材中电流密度随着传导电流和外场的幅值增加而增长。当I_m>20 A或者B_m>100 m T时, Bi-2223带材中电流密度的最大值随着传导电流和外场的幅值增加而减小, 主要原因为Bi-2223带材的临界电流随着磁场的增加出现了下降。对于频率来说, 屏蔽电流会随着外磁场的频率增加而减小, 传导电流的频率对于电流密度分布的影响可以忽略不计。当通入传导电流的Bi-2223带材放置于背景场中时, 电流密度的分布相对于中心不再对称, 并且饱和电流值会随着外磁场的幅值增加而减小。