Wind tunnel testing of wind pressures on a large gymnasium roof
来源期刊:中南大学学报(英文版)2011年第2期
论文作者:傅继阳 吴玖荣 梁枢果
文章页码:521 - 529
Key words:long-span roof; wind pressure; wind tunnel test; gymnasium roof
Abstract: A wind tunnel test was conducted for a large steel gymnasium structure. Simultaneous pressure measurements were made on its entire ellipsoidal roof in a simulated suburban boundary layer flow field. Special attention is paid to the characteristics of fluctuating wind pressures in different zones on the roof. Some selected results are presented: 1) correlations between fluctuating wind pressures on both roof surfaces, 2) eigenvalues and eigenvectors of covariance matrices of the fluctuating wind pressures, 3) probability distributions of the fluctuating wind pressures, and 4) statistical characteristics of peak factor. Furthermore, the applicability of the quasi-steady approach is discussed in detail. Based on the results, an empirical formula for estimating the minimum pressure coefficients, using a peak factor approach, is presented. Comparison of the minimum pressure coefficients determined by the proposed formula and those obtained from the wind tunnel tests is made to examine the applicability and accuracy of the proposed formula.
J. Cent. South Univ. Technol. (2011) 18: 521-529
DOI: 10.1007/s11771-011-0726-2![]()
FU Ji-yang(傅继阳)1, 2, WU Jiu-rong(吴玖荣)2, LIANG Shu-guo(梁枢果)3
1. School of Civil Engineering, Harbin Institute of Technology, Harbin 150001, China;
2. School of Civil Engineering, Guangzhou University, Guangzhou 510006, China;
3. School of Civil and Building Engineering, Wuhan University, Wuhan 430072, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: A wind tunnel test was conducted for a large steel gymnasium structure. Simultaneous pressure measurements were made on its entire ellipsoidal roof in a simulated suburban boundary layer flow field. Special attention is paid to the characteristics of fluctuating wind pressures in different zones on the roof. Some selected results are presented: 1) correlations between fluctuating wind pressures on both roof surfaces, 2) eigenvalues and eigenvectors of covariance matrices of the fluctuating wind pressures, 3) probability distributions of the fluctuating wind pressures, and 4) statistical characteristics of peak factor. Furthermore, the applicability of the quasi-steady approach is discussed in detail. Based on the results, an empirical formula for estimating the minimum pressure coefficients, using a peak factor approach, is presented. Comparison of the minimum pressure coefficients determined by the proposed formula and those obtained from the wind tunnel tests is made to examine the applicability and accuracy of the proposed formula.
Key words: long-span roof; wind pressure; wind tunnel test; gymnasium roof
1 Introduction
In recent years, many long-span roof structures have been built or are being planned throughout the world. Roofs of such structures usually have the characteristics of light weight, high flexibility, slight damping and low natural frequency. Consequently, these structures have become progressively more wind-sensitive than most conventional roof structures. Wind effects on these roofs are characterized by large uplifting pressure due to separation of wind flow at leading edges; therefore, there is a large uplifting force on such a roof [1]. This has resulted in a greater emphasis on understanding the structural behavior of these structures under wind action.
Investigations on the characteristics of wind loads and wind-induced response of large roofs have been conducted extensively. For example, MELBOURNE [2] summarized the results of the response of large roof structures through several aeroelastic model studies and proposed an empirical equation for estimating the peak design pressure coefficient for cantilevered roofs. LETCHFORD and KILLEN [3-4] reported a parametric study of wind loads on cantilevered grandstand roofs and derived equivalent static trapezoidal load distributions for the design of such structures. On the other hand, some wind loading codes and design guides provide design guidelines for simple cantilevered grandstand roofs and canopy roofs [5-6]. However, shapes of large roofs vary widely from structure to structure. It is well known that wind effects on the roof structures strongly depend on roof shape and incident wind flow characteristics. Consequently, the direct application of the above- mentioned research outputs to other kinds of large roofs may be questionable. Therefore, in designing large roofs, it is usually necessary to conduct wind tunnel tests to investigate the wind effects on these structures.
However, in many previous wind tunnel studies [7-8], due to the lack of electronic pressure scanning equipment several years ago, the wind pressures on the upper and lower roof surfaces of cantilevered roof structures were not measured simultaneously, and the peak pressures were obtained based on the data measured on the two roof surfaces separately; then an estimation of the peak net pressure coefficient was made by assuming the worst situation of peak pressures occurring at the same instant on both roof surfaces. Obviously, the adequacy of the assumption is questionable, which needs to be verified. Therefore, there is a need to further investigate this problem. On the other hand, it has been observed that much of the property damages during windstoRMS has been caused by pressure fluctuations which occur near the leading edges and corners on large roof structures. In order to reduce such wind-induced damages, it is important to improve the wind-resistance capacities of these structures. For this purpose, it is essential to understand the characteristics of wind pressure fluctuations on long-span roof structures. In general, the wind pressure fluctuations on buildings can be represented by proper orthogonal decomposition, i.e., by eigenvectors of covariance matrices of pressure fluctuations. The approach was applied to discuss the fluctuating wind pressure fields on low-rise buildings by HOLMES et al [9-10]. BIENKIEWICZ et al [11] also carried out a detailed analysis of the pressure fluctuations on a flat-roof building model by this method. However, the usage of the approach to analyze the pressure fluctuations on long-span roof structures has received little attention in the past.
In designing long-span roofs, designers are usually concerned with the maximum and minimum peak pressures irrespective of incident wind direction. The commonly used approaches for determination of local peak pressures are the quasi-steady and peak factor approaches. It is well known that the quasi-steady approach attributes all fluctuations in pressure to the fluctuations in velocity of approaching flow. The application of the approach to the prediction of minimum and root mean square (RMS) pressure coefficients on low-rise buildings was conducted by several researchers [12], and their investigations indicated that the quasi- steady theory can reasonably predict the minimum and RMS pressure coefficients. However, LETCHFORD et al [13], HOXEY et al [14] and UEMATSU and RICHARDS [15] discussed the applicability of the quasi-steady approach, and found that this approach failed where there was a significant interference to the flow by the building, such as in separated flow regions where pressure fluctuations were influenced by building-generated or wake turbulence.
The peak factor approach is a pragmatic method which seeks to alleviate the deficiency of the quasi-steady approach [16]. When the method is to be used for design, a great difficulty is how to select a suitable value of peak factor. LEVITAN et al [17], OKADA and HA [18] showed that the peak factors for negative pressures on a flat roof ranged from 4 to 7, which were determined by full-scale and wind tunnel measurements for the Texas Tech building. A quite enormous range of the peak factors from 4 to 10 was also found by UEMATSU and ISYUMOV [19] based on their wind tunnel tests for low-rise buildings. A rational approach to obtain the peak factor is to determine the probability distribution of fluctuating pressures and to select a peak factor corresponding to a given probability level. For example, for a normal distribution corresponding to a probability level of 10-5, the peak factor is 4, which is frequently adopted for structural design [16]. However, some measurements [20] showed that the probability density functions of fluctuating wind pressures in separated flow regions departed significantly from Gaussian distribution; therefore, for a given probability level, the values of the peak factor in these regions apparently varied without a coherent pattern [16]. For the sake of simplicity, an equivalent peak factor averaged for all locations and wind directions tested was adopted in many studies [16, 19]. However, most of the previous studies related to the quasi-steady and peak factor approaches were mainly concerned with low-rise buildings; few studies have been conducted for long-span roof structures in the past. The objective of this study is to improve the understanding of the characteristics of fluctuating wind pressures on a typical large gymnasium roof in general, to discuss the applicability of the quasi-steady approach and to explore how to estimate the minimum pressure coefficients in particular.
2 Wind tunnel experiments
2.1 Experimental arrangements
Wind tunnel tests were conducted for a large steel gymnasium structure, located in China, as shown in Fig.1. The basic plan form of the roof of the gymnasium is essentially elliptical with a mean roof height of 30 m above ground. The lengths of the two diameters of the ellipse are 165 m and 145 m, respectively.

Fig.1 Model in wind tunnel tests
In the wind tunnel experiments, a rigid model with a geometric length scale of 1:200 was made to represent the gymnasium; all major surrounding buildings were also reproduced at a geometric scale of 1:200, including a natatorium, a tennis court and some accessorial low-rise buildings.
Wind tunnel experiments were carried out in the boundary layer wind tunnel at Shantou University with a working section of 3 m wide, 2 m high and 20 m long. Fig.1 shows a photo of the models mounted in the wind tunnel. Spires and roughness elements were used to simulate a boundary layer wind flow of suburban terrain type specified in the China Load Code [20] as exposure B. This terrain type specifies a mean wind speed profile with a power law exponent of α=0.16. The measured mean wind speeds and turbulence intensities at various heights over the test section are illustrated in Fig.2 and Fig.3, respectively. Meanwhile, the turbulence intensity profile specified by AIJ 1996 [21] is also shown in Fig.3 for comparison purposes, and it is found that the turbulence intensity at the model’s mean roof height (H, 0.15 m in the wind tunnel) IuH is about 15%. The spectrum of longitudinal wind velocity at the height of 45 m (0.225 m in the wind tunnel) is shown in Fig.4, which agrees with the Karman type spectrum well. In this figure, the reduced power spectra and frequencies are expressed as the non-dimensional forms, fSu(f)/σ2 and fz/Uz, respectively.
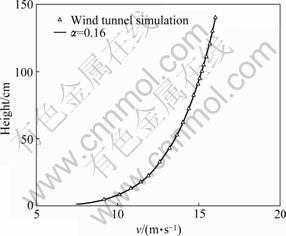
Fig.2 Mean wind speed profile
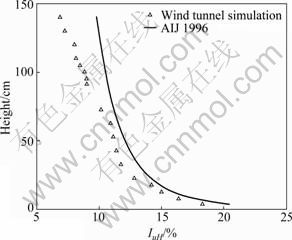
Fig.3 Turbulence intensity profile
There were 199 and 48 pressure taps made on the upper and lower roof surfaces, respectively, for pressure measurements. The layout of the pressure taps on the upper roof surface is shown in Fig.5. In order to obtain the pressure differences between both sides of the cantilevered roof parts, 48 pairs of pressure taps were installed at the same locations on both upper and lower cantilevered roof surfaces, which are marked with “○” shown in Fig.5. The other 151 pressure taps marked with “●” and “+” shown in Fig.5 were arranged on the upper surface of the enclosed section of the roof.

Fig.4 Spectra of longitudinal wind velocity at height of 45 m in full-scale
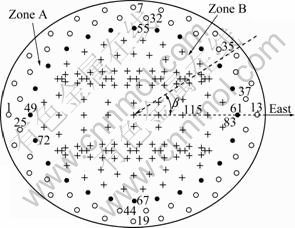
Fig.5 Layout of pressure taps on upper roof surface
2.2 Pressure measurements and data analysis
In the wind tunnel tests, pressures were measured simultaneously from all the taps on both roof surfaces, and the data sampling frequency was 312.5 Hz with sampling length of 16 384. Wind direction was defined as an angle β from the east along anti-clockwise direction and β varied from 0° to 360° with incremental step of 15°, as shown in Fig.5.
The pressure measurements were carried out at a wind velocity of uref=14.2 m/s at a reference height of zref=145 cm. The pressure coefficient of the pressure tap i on the roof surface is defined as
![]() (1)
(1)
where pi(t) is the measured surface pressure at tap i; p0 and p∞ are the total pressure and the static pressure at the reference height, respectively.
The convention for positive roof pressure and the corresponding pressure coefficient, on either the upper or lower roof surface, is always from the air side onto the roof surface. The net wind-induced pressure on the cantilevered roof parts due to the combined action of the pressures on the upper and lower roof surfaces are defined to be positive in the downward direction:
![]() (2)
(2)
where ![]() is the pressure difference coefficient of tap i between the upper and lower roof surfaces;
is the pressure difference coefficient of tap i between the upper and lower roof surfaces; ![]() and
and ![]() are the measured upper and lower surface pressures at tap i, respectively.
are the measured upper and lower surface pressures at tap i, respectively.
The design wind speed with 50-year return period for the district where the gymnasium is located is about 41.4 m/s at the height of 290 m [22]. Therefore, the velocity scale in the wind tunnel experiments is about 14.2/41.4=1/2.9, and the time scale becomes 1/69. Then, the sampling frequency and record length in the pressure measurements are equivalent to 4.53 Hz and 60.3 min in full scale, respectively. The period for evaluating the statistics of pressure fluctuations was taken to be 10 min, which is usually used as the average time in wind speed measurements in China [20]. The record time is divided into consecutive 10 min periods and the pressures at tap i are analyzed as mean, RMS, maximum and minimum pressure coefficients, Cpmean, Cpirms, Cpimax and Cpimin for each period. From a 60.3 min record, the pressure coefficients can be obtained from six data recording segments, the averages of which are used in the following analysis.
3 Results and discussion
3.1 Cross-correlation coefficients
It is important to know how the fluctuating wind pressures on the upper roof surface are correlated with those on the lower roof surface. Such a cross correlation can be quantified by taking the mean of the product of the signal from the upper roof surface at time t and the signal from the lower roof surface at time (t + τ), where τ is a time lag between the two sets of signals. The cross-correlation coefficient Rul(τ) is defined as the cross correlation divided by the product of the standard deviations of the two sets of signals.
The sign of the cross-correlation coefficient at τ=0 depends upon how often the sign of pressure fluctuations coincide with each other [23]. Fig.6 shows the fluctuating pressure cross-correlation coefficients Rul(τ) at τ=0 for each pair of the pressure taps marked with “○” shown in Fig.5 on the cantilevered roof parts under three typical approaching wind directions. It can be seen from Fig.6 that the values of the cross-correlation coefficients vary rapidly with the pressure tap location and the approaching wind direction; but the values are usually negative near the windward roof edges and positive in other regions. It is well known that the loads acting on the cantilevered roof parts are a combination of wind pressures on both roof surfaces [1, 23], thus the fluctuating pressure cross-correlation coefficients can significantly affect the net pressures acting on the roof. Therefore, for the determination of the design loads on a cantilevered roof, the wind pressures should be measured simultaneously on both roof surfaces in wind tunnel tests.
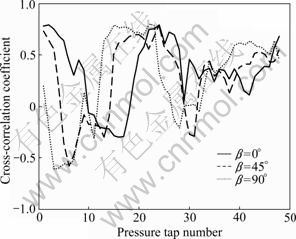
Fig.6 Cross-correlation coefficients of fluctuating pressures between upper and lower surfaces
3.2 Eigenvalue and eigenvector
The fundamental quantity which contains basic statistical information, both on the magnitude of the pressure fluctuations at a tap, or on a discrete area, of a building, as well as the relationship with the pressure fluctuations at other taps on the building, is the covariance Cij [24], which is defined as
![]() (3)
(3)
where ![]() represent the fluctuating pressures at taps i, j, respectively, and the overbar indicates a time average.
represent the fluctuating pressures at taps i, j, respectively, and the overbar indicates a time average.
Since the pressure data in wind tunnel tests are normally expressed in terms of non-dimensional pressure coefficients, Eq.(3) can be expressed as
![]() (4)
(4)
where ![]() are the RMS fluctuating pressure coefficients at taps i and j, respectively.
are the RMS fluctuating pressure coefficients at taps i and j, respectively.
In order to further understand the fluctuating pressure patterns in different zones on the roof, an eigenvector/eigenvalue analysis is undertaken to analyze two covariance matrices obtained from two different pressure fields without inclusion of mean value components. One was obtained based on simultaneously recorded time histories of pressure data from 72 pressure taps (marked with “○” and “●” shown in Fig.5, zone A) located at the leading edges of the roof for an approaching wind direction of 0°; the other was determined from the simultaneous measurements from 127 pressure taps (marked with “+”, shown in Fig.5, zone B) located in the middle parts of the roof for the same incident wind direction. Then, the eigenvalues and eigenvectors are obtained by solving the eigenvalue problem for the two cases, respectively. It should be pointed out that for the cantilevered roof parts, the time histories of pressure data are the fluctuating pressure differences.
Table 1 lists the relative contributions from the first ten eigenvalues for zones A and B. It can be seen from Table 1 that the first ten eigenvalues contribute most of the total fluctuating pressure energy in each case. Moreover, the contribution from the first eigenvalue is principal for both cases, which indicates that the proportion of the first eigenvalue is principal in representing the fluctuating pressure fields.
Table 1 Relative contributions from first ten eigenvalues for zones A and B on roof

Figs.7(a) and (b) show the comparisons between the first eigenvector and the mean pressure coefficient distribution for zones A and B, respectively. It can be seen from Fig.7(b) that there is a striking similarity between the two sets of data for zone B. However, it is found from Fig.7(a) that the similarity is not applicable to zone A, i.e., the first eigenvector does not follow the mean pressure coefficient distribution in zone A. This may be due to the fact that the pressure fluctuations in zone A are affected by the building-generated turbulence as well as by the turbulence of the approaching flow, since the pressure taps in zone A are mainly under separated and reattaching flows. The observations imply that the quasi-steady theory may be applied to the middle parts of the roof, but would fail at the leading edges of the roof.

Fig.7 Comparisons of first eigenvector and Cpmean: (a) Zone A; (b) Zone B
3.3 Probability density function and peak factor
The probability density functions (PDF) were determined by the calculation of the marginal histograms of the pressure fluctuations [25] in order to investigate the probability characteristics of the fluctuating pressures in different zones on the roof.
Figs.8(a) and (b) show the probability density functions of the fluctuating pressure differences measured at pressure taps 83 and 115 shown in Fig.5 for a wind direction of 0°. Taps 83 and 115 are both located in the middle parts of the roof (zone B). In these figures, probability density functions of the normal distribution are plotted for comparison; and plotting the histograms of the normalized time histories (Cp-Cpmean)/Cprms in logarithmic scale makes it apparent that how the tails of the measured probability density functions deviate from those of the normal distributions.
It can be seen from Figs.8(a) and (b) that the two measured probability density functions approximately follow the normal distribution; then the peak factors for both cases were determined to be about 4 for a probability level of 10-5 [16]. Furthermore, it is found that the tendency can also be applied to most of the pressure taps in zone B, when these pressure tap locations are on the upstream face. Therefore, as a representative value in this region, we can use peak factor g=4 for zone B. In fact, the value of g approximately corresponds to that of the equivalent peak factor (3.91) averaged for all pressure taps in zone B under all wind directions.

Fig.8 Probability density functions of fluctuating pressure differences: (a) Tap 83; (b) Tap 115
Figs.9(a) and (b) present the probability density functions of the fluctuating pressure differences measured at pressure taps 13 and 35 shown in Fig.5 for the incident wind direction of 0°. Taps 13 and 35 are both located at the leading edges of the roof (zone A). The probability density functions presented in these figures are clearly negative-skewed, as noted by previous researchers [20, 25]. The probability density functions of the fluctuating pressure differences obtained based on the experimental data are distinctly different from the normal distribution, particularly for the tails. This may be attributed to the fact that the two taps were under separated flows [20]. It can also be seen from these figures that the actual probability distributions have much longer negative tails than positive ones. This indicates that there exists a much higher probability for occurrence of larger negative pressures than that predicted by a Gaussian distribution.
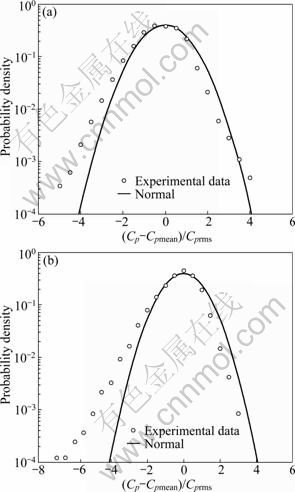
Fig.9 Probability density functions of fluctuating pressure differences: (a) Tap 13; (b) Tap 35
For pressure tap 13, the peak factor g is close to 5 at a probability level of 10-5; but for pressure tap 35, the peak factor g at the same probability level is about 7. Furthermore, it is found that the measured probability density functions for most of the pressure taps in zone A under different wind directions demonstrate non- Gaussian distributions. Then, a quite enormous range of the peak factor from 4 to 10 at the probability level of 10-5 are found in zone A; moreover, the peak factor changes rapidly with the pressure tap location and incident wind direction. Therefore, it is very difficult to find a coherent pattern to describe the variation.
In order to obtain a representative peak factor for zone A, the peak factors for all pressure taps in this region under incident wind directions of 0° and 90° are plotted in Figs.10(a) and (b), respectively, against the minimum pressure coefficient Cpmin. From the wind tunnel experimental results, the wind loads on the cantilevered roof parts are mainly dominant by relatively high negative wind pressures; therefore, the peak factors corresponding to the minimum pressure coefficients are defined as
![]() (5)
(5)
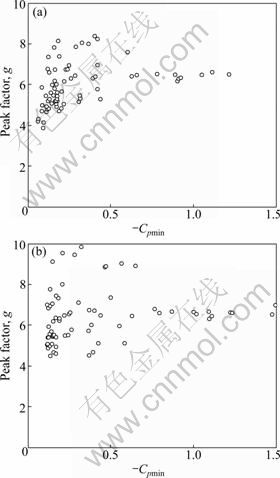
Fig.10 Peak factor g versus Cpmin: (a) β=0°; (b) β=90°
It can be seen from these figures that when the magnitude of Cpmin is relatively small, the scatter of the results is considerable; however, as the value of |Cpmin| increases, the values of the peak factors collapse into a relatively narrow range and are very close to 6.5. Therefore, as a representative value in zone A, it is reasonable to choose g=6.5. In fact, the value of g approximately approaches to the value of the equivalent peak factor (6.43) averaged for all pressure taps in zone A under all wind directions.
3.4 Quasi-steady theory
The application of the quasi-steady theory to the prediction of RMS pressure coefficients on low-rise buildings has been investigated by several researchers [13], but the usage of this approach to predict the RMS pressure coefficients on large cantilevered roof structures has received little attention in the past. Using the first-order quasi-steady theory model, in which only the longitudinal turbulence of the approaching flow is considered, CpRMS may be determined by the following equation:
![]() (6)
(6)
In order to verify the applicability of the quasi-steady approach in different zones on the roof, the values of CpRMS/(2IuH|Cpmean|) for all taps in zones A and B on the roof in wind directions of 0? and 90? are plotted in Figs.11(a) and (b), respectively. It should be pointed out that some pressure taps on the downstream side where turbulence was generated in the boundary layer shear flows on the building surface are exclusive from these figures. For these pressure taps, the values of CpRMS/(2IuH|Cpmean|) may be very large in some cases, but the magnitudes of the mean, RMS and minimum pressure coefficients are generally small, then the wind pressures for these pressure taps have no significant effect on the whole characteristics of wind pressure distributions on the roof. Therefore, these pressure taps are exclusive from Figs.11(a) and (b).
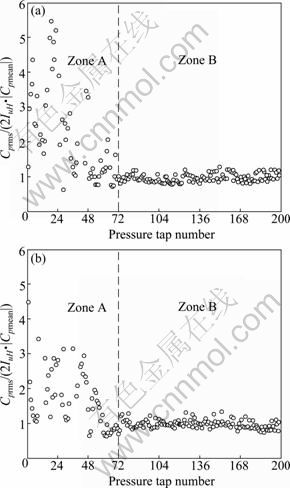
Fig.11 CpRMS/(2IuH|Cpmean|) versus pressure tap number: (a) β=0°; (b) β=90°
It can be seen from Figs.11(a) and (b) that for zone B, the ratio is almost constant, approximately 1.0, in the whole area. This indicates that in zone B, the quasi-steady theory can be applied to predict the RMS pressure coefficients. On the other hand, for zone A, the data exhibit a considerable scatter. This suggests that the pressure fluctuations in zone A are significantly affected by the building-generated turbulence as well as by the turbulence of approaching flow, since these taps are under separated and reattaching flows. Therefore, it can be concluded that the quasi-steady theory can be applied to predict the RMS pressure coefficients in zone B on the roof, but would fail in zone A.
4 Empirical formula
From the wind tunnel experimental results, the wind loads on the large roof are dominant by relatively high negative wind pressures. Therefore, in designing the roof, the primary focus is on the determination of the minimum pressure coefficients, especially the minimum pressure coefficients irrespective of approaching wind direction.
Considering the above-presented results, we can evaluate the minimum pressure coefficients in different zones on the roof using the following equations:
 (7)
(7)
Fig.12 shows the comparison between the wind tunnel experimental results and those obtained by the proposed formula for the minimum pressure coefficient irrespective of the wind direction. In this figure, the measured data and the predicted results for all pressure taps in zones A and B on the roof are plotted. It can be seen from Fig.12 that the results predicted by the formula are in good agreement with the experimental data. In fact, the agreement between the two sets of data is satisfactory at least for engineering practice, thus illustrating that the proposed formula can provide satisfactory predictions of the minimum pressure coefficients on the roof.
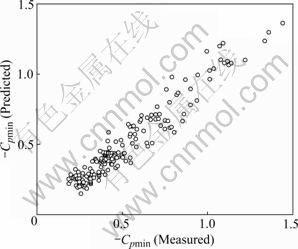
Fig.12 Comparison of results from formula and experimental data of minimum pressure coefficient
5 Conclusions
1) The wind loads acting on the roof are a combination of wind pressures on both roof surfaces, and the fluctuating pressure cross-correlation coefficients can significantly affect the net pressures acting on the roof. Therefore, for the determination of the design loads on a cantilevered roof, the wind pressures should be measured simultaneously on both roof surfaces in wind tunnel tests.
2) An eigenvalue/eigenvector analysis of fluctuating pressures on the roof reveals that the first ten eigenvalues contribute most of the total fluctuating pressure energy, and the proportion of the first eigenvalue is principal in representing the fluctuating pressure fields. In the middle parts of the roof, the first eigenvector follows the similar distribution with that of the mean pressure coefficient, but the similarity is not applicable to the leading edges of the roof.
3) The measured probability density functions approximately follow the normal distribution in the middle parts of the roof; but at the leading edges of the roof, the measured probability density functions are clearly negative-skewed and distinctly different from the normal distribution, particularly for the tails.
4) In the middle parts of the roof, the peak factor is about 4 at a probability level of 10-5. However, a quite enormous range of the peak factor from 4 to 10 at the probability significance level are found at the leading edges of the roof; moreover, the peak factor changes rapidly with the pressure tap location and incident wind direction, and its value is about 6.5 where severe suctions occur.
5) The quasi-steady theory can be applied to the evaluation of RMS pressure coefficients in the middle parts of the roof, but would fail at the leading edges of the roof.
6) Based on the above mentioned findings, an empirical formula was proposed for estimating the minimum pressure coefficients on the roof. It was found that the results determined from the formula are in good agreement with the experimental data. In fact, the agreement between the two sets of data is satisfactory at least for engineering practice, suggesting that the formula is applicable to engineering applications.
References
[1] LAM K M, ZHAO J G. Occurrence of peak lifting actions on a large horizontal cantilevered roof [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(8): 897-940.
[2] MELBOURNE W H. Response of large roofs to wind action [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 54/55(1): 325-335.
[3] KILLEN G P, LETCHFORD C W. A parametric study of wind loads on grandstand roofs [J]. Engineering Structures, 2001, 23(6): 725-735.
[4] LETCHFORD C W, KILLEN G P. Equivalent static wind loads for cantilevered grandstand roofs [J]. Engineering Structures, 2002, 24(2): 207-217.
[5] AS1170.2-1989, Australian Wind Loading Code [S].
[6] COOK N J. The designer’s guide to the wind loading of building structures. Part 2: Static structures [R]. London: BRE/Butterworths, 1990.
[7] MARIGHETTI J, WITTWER A, BORTOLI M D, DE BORTOLI M, NATALINI B, PALUCH M, NATALINI M. Fluctuating and mean pressure measurements on a stadium covering in wind tunnel [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 84(3): 321-328.
[8] ZHU L D, CHEN W, SHI Z C, ZHANG F. Wind pressure distribution on a stadium roof by wind tunnel model test [C]// 10th International Conference on Wind Engineering, Copenhagen, Denmark, 1999: 1583-1590.
[9] HOLMES J D. Optimized peak load distributions [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 41(1/2/3): 267-276.
[10] HOLMES J D, SANKARAN R, KWOK K C S, SYME M J. Eigenvector modes of fluctuating pressures on low-rise building models [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 69/70/71(1): 697-707.
[11] BIENKIEWICZ B, TAMURA Y, HAM H J, UEDA H, HIBI K. Proper orthogonal decomposition and reconstruction of multi- channel roof pressure [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 54/55(1): 369-381.
[12] KIND R J. Worst suctions near edges of flat rooftops with parapets [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 31(2/3): 251-264.
[13] LETCHFORD C W, IVERSON R E, MCDONALD J R. Application of the quasi-steady theory to full scale measurements on the Texas Tech Building [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 48(1): 111-132.
[14] HOXEY R P, RICHARDS P J. Full-scale wind load measurements point the way forward [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 57(2/3): 215-224.
[15] UEMATSU Y, ISYUMOV N. Review: Wind pressures acting on low-rise buildings [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 82(1): 1-25.
[16] COOK N J. Calibration of the quasi-static and peak-factor approaches to the assessment of wind loads against the method of Cook and Mayne [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1982, 10(3): 315-341.
[17] LEVITAN M L, MEHTA K C, VANN W P, HOLMES J D. Field measurements of pressures on the Texas Tech building [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1991, 38(2/3): 227-234.
[18] OKADA H, HA Y C. Comparison of wind tunnel and full-scale pressure measurement tests on the Texas Tech building [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 43(3): 1601-1612.
[19] UEMATSU Y, ISYUMOV N. Peak gust pressures acting on the roof and wall edges of a low-rise building [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 77/78(1): 217-231.
[20] GB50009—2001. Load code for the design of building structures [S]. (in Chinese)
[21] AIJ Recommendations for Loads on Buildings (English version) [R]. Tokyo: Architectural Institute of Japan, 1996.
[22] LI Q S, CALDERONE I, MELBOURNE W H. Probabilistic characteristics of pressure fluctuations in separated and reattaching flows for various free-stream turbulences [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 82(1): 125-145.
[23] BESTTE F, CETMAK J E. Correlation of internal and area-averaged external wind pressures on low-rise buildings [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 69/70/71(1): 557- 566.
[24] HOLMES J D. Analysis and synthesis of pressure fluctuations on bluff bodies using eigenvectors [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1990, 33(1/2): 219-230.
[25] GIOFFRE M, GUSELLA V, GRIGORIU M. Non-Gaussian wind pressure on prismatic buildings. I: Stochastic field [J]. Journal of Structural Engineering ASCE, 2001, 127(9): 981-989.
(Edited by YANG Bing)
Foundation item: Project(50978063) supported by the National Science Foundation of China; Project(NCET-09-0082) supported by the Program for New Century Excellent Talents in Chinese Universities; Project(121072) supported by the Fok Ying-Tong Education Foundation for Young Teachers in the Higher Education Institutions of China
Received date: 2010-05-21; Accepted date: 2011-01-24
Corresponding author: FU Ji-yang, Professor, PhD; Tel: +86-20-39366430; E-mail: jiyangfu@yahoo.com.cn

