Flow stress and microstructure evolution of semi-continuous casting

AZ70 Mg-alloy during hot compression deformation

GUAN Shao-kang(关绍康), WU Li-hong(吴立鸿), WANG Li-guo(王利国)

School of Materials Science and Engineering, Zhengzhou University, Zhengzhou 450002, China

Received 18 May 2007; accepted 23 August 2007

Abstract: To evaluate and predict flow stress and set up hot forging process of AZ70 magnesium alloy, hot compression tests of AZ70 magnesium alloy were carried out on Gleeble 1500D thermo-mechanics tester at 300-420 ℃ and strain rates of 0.001-1 s^-1 with different compression degrees. It is indicated that temperature and strain rate are the main factor affecting the flow stress and microstructure. Stress increases but average grain size decreases with temperature decreasing and strain rate increasing. The stress model, constituted by introducing temperature-compensated strain rate, the Zener-Hollomon parameter, has a good fitness with the proof stress value under the experimental condition. The reciprocal of grain size at true strain of 1.0 has a linear relation with natural logarithm of Z parameter, and the correlation coefficient, R=0.95, is very significant by examination. The hot deformation activation energy Q of AZ70 alloy is 166.197 kJ/mol by calculation.

Key words: AZ70 Mg-alloy; flow stress; Zener-Hollomon parameter; microstructure evolution

1 Introduction

Compared with magnesium alloy castings, magnesium alloy forgings possess greater potential due to higher strength, better plasticity and various mechanical properties, but they are still used in narrow fields and relatively small quantities[1-2]. This is mainly because magnesium alloy has a closed-packed hexagonal (HCP) crystal structure with poor formability at room temperature[3]. Generally hot forging is one of the most efficient ways to improve the formability and attain high-property structural parts. Even then, magnesium alloy of the kind is still limited to a small quantity. Mg-Al-Zn alloy system is a most common-used one available for hot forging because of its abundant raw materials, low price and moderate properties. Recently, a majority of investigations have been reported on AZ31 alloy[4] and its simple-shaped wrought products like extruded bars, tubes, sections, etc., and a minority on AZ91 and others[5-7]. It has been shown that Mg-Al-Zn system alloy forgings with approximately 7.0% Al content perform attractive combined properties of high strength, moderate plasticity and toughness[2,8-9]. Consequently, AZ70 Mg alloy was selected in the work.

To numerically simulate and evaluate hot forging process with the aim of predicting the optimum process parameters, the flow stress and microstructure at elevated temperatures were measured using Gleeble 1500D simulator and the stress model was constituted according to measured data by introducing Z parameter.

2 Experimental

The material used in the present study was AZ70 magnesium alloy billet prepared by using a semi-continuous casting method, followed by homogeneous annealing in air at 410 ℃ for 10-15 h. The chemical compositions of 7.12%Al, 0.37%Zn, 0.22%Mn, 0.01%Si, ≤0.005%Fe, ≤0.005%Cu, ≤0.005%Ni and balance Mg were revealed by glow discharge spectroscopy. The microstructure of AZ70 is shown in Fig.1. Compression specimens were cut along extruded direction of the billet and machined into small cylinder samples of d 10 mm×15 mm. Compression test was conducted in air on Gleeble 1500D thermo- mechanics simulator in the temperature range from 300 to 420 ℃ and at strain rates of 0.001-1 s^-1. Graphite flakes were located on the end surfaces of specimens in order to improve lubrication. Final true strain values of all specimens are 1.0. The test data were recorded automatically. After each test, all compressive specimens were water-quenched immediately to preserve the elevated temperature microstructure. Specimens for optical morphology were sectioned along axial direction, mounted, polished and then etched in acetic picral. Average grain sizes were inspected based on intercept method given in the Ref.[10].

Fig.1 Microstructure of AZ70 alloy homogenized

3 Results and discussion

3.1 Flow stress characteristics of AZ70

True flow stress—strain curves of AZ70 Mg alloy at different temperatures and various strain rates are illustrated in Fig.2, which reflect the influences of temperature, strain rate and strain on flow stress. From Fig.2, it can be seen that the curves of AZ70 alloy exhibit that typical dynamical crystalline(DRX) characteristics during the test of compression play dominant role. All curves exhibit a sharp increase of the initial stage of strain and then slowly increase up to a transient equilibrium, when stress arrives at the maximum value. Subsequently stress decreases and then drives to a steady value with increasing strain. Fig.3 reveals that flow stress is significantly affected by temperature and strain rates, namely, the peak and steady stresses at the same strain increase with temperature decreasing and strain rate increasing. With strain rate decreasing, there is a weak effect of temperature on stress. Consequently, AZ70 alloy belongs to a material with positive strain rate sensitivity.

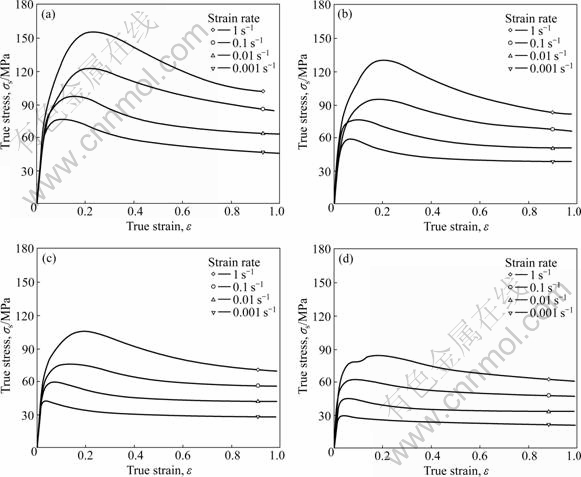
Fig.2 True stress—strain curves of AZ70 Mg alloy at various strain rates and different temperatures: (a) 300 ℃; (b) 340 ℃; (c) 380℃; (d) 420 ℃

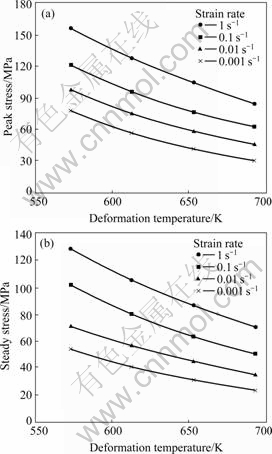
Fig.3 Peak (a) and steady (b) stress of AZ70 Mg alloy at elevated temperatures

3.2 Flow stress model

For commonly used metal materials, to describe precisely the relation between flow stress and deformation temperature, strain rate and strain, a flow stress model is generally obtained by modifying Arrhenius equation[11-12], which is adequately expressed into three forms, namely, law (Eqn.(1)), exponent (Eqn.(2)) and hyperbolic sine function(Eqn.(3)) respectively[6,13-14]:

                      (1)

                (2)

             (3)

Eqns.(1) and (2) are usually given at low and high stress levels respectively, but Eqn.(3) covers all stress ranges[6]. A, A₁, A₂, α, β, n and n₁ are all constants, 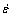 is strain rate, T is temperature, R is universal gas constant with the value of 8.31 J?mol^-1?K^-1, and Q is deformation activity energy.

The relation plots of flow stress vs. strain rate, deformation temperature and strain obtained by experimental data are shown in Figs.4-6 respectively. From these figures, it is evident that there is a linear relation of flow stress vs. reciprocal of deformation temperature, strain rate in natural logarithm scale and strain in natural logarithm scale, respectively. Consequently flow stress model can be described by exponent function equation. Considering the effect of strain on flow stress, the flow stress model can be expressed by

              (4)

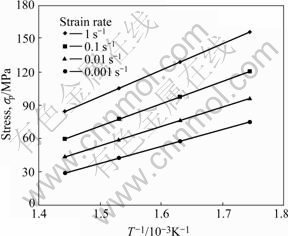
Fig.4 Relation between peak stress and temperature of AZ70

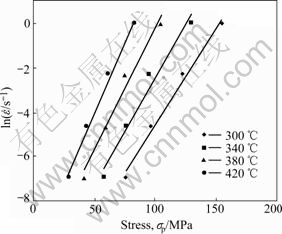
Fig.5 Relation between strain rate and peak stress

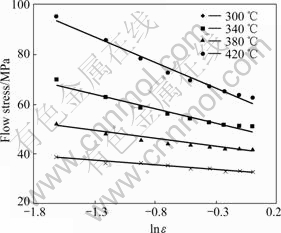
Fig.6 Relation of stress and strain of AZ70 at strain rate of  0.01 s^-1

The above equation can be expressed into Eqn.(5) by introducing Z parameter:

                     (5)

where 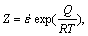 Z is Zener-Hollomon parameter

combining the two control variables through an Arrhenius equation with activation energy Q[15-17]. By taking natural logarithms for Eqn.(2) and differentiating it with respect to 1/T, the deformation activity energy can be expressed as follows:

        (6)

The values of  and  can be obtained by linear regression analysis, as illustrated in Figs.4 and 5, so the deformation activity energy of AZ70 alloy is Q=166.197 kJ/mol by calculation.

After being taken for natural logarithm, Eqn.(5) is transformed and expressed as

                         (7)

To describe precisely the relation of flow stress, deformation temperature, strain rate and strain, the above equation is further modified and can be expressed as

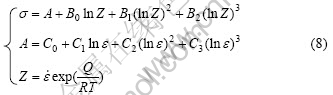
where  A, B₀, B₁, B₂, C₀, C₁, C₂ and C₃ are all material parameters of the modified model, which are listed in Table 1 by regression calculation.

Table 1 Material parameters for modified model

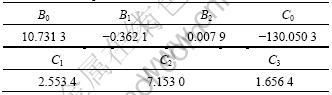
Fig.7 illustrates the comparison of the calculated stresses by the modified model with the experimental ones for AZ70 at different temperatures. It is indicated that calculated stresses have a good fitness with experi- mental ones. By deviation calculation under all the experimental conditions, the maximum and total mean square deviations are 7.47 and 5.03, respectively.

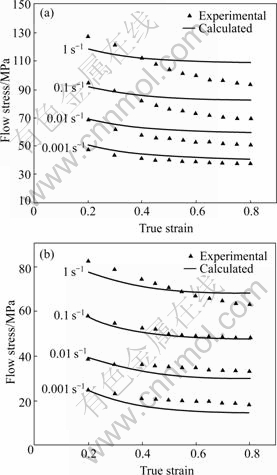
Fig.7 Comparison of calculated stress with experimental stress for AZ70 alloy: (a) 340 ℃; (b) 420 ℃

3.3 Microstructure evolution

Fig.8 shows the final deformation microstructures of AZ70 at different temperatures with strain rate of 0.1 s^-1. At the comparatively low temperature of 300 ℃, the deformation microstructure is still dominant, and small amount of recrystallized sub-grains distribute along deformation grain boundaries (in Fig.8(a)). With temperature increasing, large numbers of recrystallized grains distributing along deformation grain boundaries nucleate and grow up, which results in the replacement and gradual disappearing of deformation grain. At high temperature of 380-420 ℃, deformation grains are almost replaced with complete recrystallized grains. As shown in Figs.8(c) and (d), it can be seen that the microstructures reveal complete recrystallized microstructure. With strain rate decreasing, recrystallized grains are prone to coarsening, which are illustrated in Fig.9.

Fig.8 Final deformation microstructures at strain rate of 0.1 s^-1 at different temperatures: (a) 300 ℃; (b) 340 ℃; (c) 380 ℃; (d) 420 ℃

Fig.9 Final deformation microstructures at 380 ℃ with different strain rates: (a) 1 s^-1, (b) 0.01 s^-1; (c) 0.001 s^-1
 

Similar to stress, the effect of temperature and strain rate on average grain size can also be expressed by introducing Z parameter, where grain size of compression specimen at 300 ℃ with strain rate of 1 s^-1 is not included due to its crack. By linear regression, the reciprocal of grain size has a linear relation with natural logarithm of Z parameter. Regression equation should be described as Eqn.(9), and the correlative coefficient, R, is equal to 0.95 by examination:

1/d=0.008 2 lnZ-0.123 3                       (9)

So the regression equation possesses remarkable correlation, and it can reasonably reflect the change of grain size with temperature and strain rate.

4 Conclusions

1) The flow stress curves of AZ70 alloy exhibit that typical DRX characteristics during the compression test play dominant role. Stress at the same strain increases with temperature decreasing and strain rate increasing.

2) The stress model of AZ70 alloy is obtained based on Arrhenius equation by introducing Zener-Hollomon parameter. The stress predicted by the model matches well with that measured from the experiment. Consequently, the model can provide a theoretical guideline on hot forging process and numerical simulation of AZ70 alloy.

3) Deformation grains play dominant role at low temperature and high strain rate. With temperature increasing and strain rate decreasing, microstructures are transformed from mixed crystal and uncompleted strip-shaped recrystallization to completed recrystallization, and average grains size increases simultaneously. The reciprocal of grain size has a linear relation with natural logarithm of Z parameter.

Acknowledgements

The author sincerely thanks Prof. NIU Ji-tai from Harbin Institute of Technology, China for advice and help in thermo-mechanic simulation experiment and director SHI Jun-mei from Jiaozuo Yellow River MG Alloy Product Co. Ltd, China for preparation of alloy billet.

  References

[1] MORDIKE B L, EBERT T. Magnesium: Properties—applications— potential [J]. Materials Science Engineering A, 2001, 302: 37-45.

[2] WU Li-hong, GUAN Shao-kang, WANG Li-guo, LIU Jun. Wrought magnesium alloys and several key factors affecting the forging forming [J]. Forging Tech, 2006, 31: 7-10.

[3] AGHION E, ELIEZER D. Magnesium alloys science, technology and application [M]. Haifa: Israel Consortium for the Development of Magnesium Technology, 2004.

[4] TAKUDA H, MORISHITA T, KINOSHITA T. Modelling of formula for flow stress of a magnesium alloy AZ31 sheet at elevated temperatures [J]. Journal of Materials Processing Technology, 2005, 164/165: 1258-1262.

[5] CHINO Y, KOBATA M, IWASAKI H, MABUCHI M. An investigation of compressive deformation behaviour for AZ91 Mg alloy containing a small volume of liquid [J]. Acta Materialia, 2003, 51: 3309-3318.

[6] TAKUDA H, FUJIMOTO H, HATTA N. Modelling on flow stress of Mg-Al-Zn alloys at elevated temperatures [J]. Journal of Materials Processing Technology, 1998, 80/81: 513-516.

[7] TROJANOV? Z, LUK?? P. Compressive deformation behaviour of magnesium alloys [J]. Journal of Materials Processing Technology, 2005, 162/163: 416-421.

[8] ZHANG Xiao-liang, TANG Xin-min. Characteristics of forging magnesium materials and application in vehicle wheel [J]. Foreign Metal Heat Treatment, 1998, 4: 38-40.

[9] WU Li-hong, LIU Jun, GUAN Shao-kang, GAO Ya, WANG Song-jie. Effect of Sn addition on microstructure and room temperature compression properties of AZ70 Mg-alloy [J]. Hot Working Technology, 2006, 35: 13-16.

[10] GB/T 4296—2004. Inspection method for microstructure of wrought magnesium alloy [S]. Beijing: Standards Press of China, 2004.

[11] LI Miao-quan, LI Xiao-li, LONG Li, XU Guang-xing, YU Hao, CHI Cai-lou, WEN Guo-hua. Deformation behavior and processing map of high temperature deformation of TA15 alloy [J]. Rare Metal Materials and Engineering, 2006, 35(9): 1354-1358. (in Chinese)

[12] WU Li-hong, WANG Li-guo, GUAN Shao-kang, LIU Jun, CHEN Yong. Constituting technology of hot deformation resistances model for Mg-alloys [J]. Forging Tech, 2007, 32: 106-110.

[13] SHENG Z Q, SHIVPURI R. Modeling flow stress of magnesium alloys at elevated temperature [J]. Materials Science and Engineering A, 2006, 419: 202-208.

[14] BARNETT M R. Influence of deformation conditions and texture on the high temperature flow stress of magnesium AZ31 [J]. J Light Met, 2001, 1(3): 167-177.

[15] SELLARS C M. Hot workability [J]. Int Metallurg Rev, 1972, 17: 1-24.

[16] YU Kun, LI Wen-xian, ZHAO Jun, MA Zheng-qing, WANG Ri-chu. Plastic deformation behaviors of a Mg-Ce-Zn-Zr alloy [J]. Scripta Materialia, 2003, 48: 1319-1323.

[17] GUO Qiang, YAN Hong-ge, CHEN Zhen-hua, ZHAN Guo-hui. Hot compression deformation behavior of AZ31 magnesium alloy at elevated temperature [J]. The Chinese Journal of Nonferrous Metals, 2005, 15(6): 900-906. (in Chinese)

Foundation item: Project(204085) supported by Key Project of Educational Ministry of China

Corresponding author: WU Li-hong; Tel: +86-371-63886170; E-mail: lhxw1129@126.com

(Edited by YANG Bing)