DOI: 10.11817/j.issn.1672-7207.2016.05.004

氧气高炉新型氧煤燃烧器设计参数对风口区流场影响数值模拟

张超，张建良，孙辉，刘征建

 (北京科技大学 冶金与生态工程学院，北京，100083)

摘要：氧气高炉通过向风口回旋区喷吹煤粉以及脱除CO₂的循环高炉煤气，可有效降低CO₂排放。运用CFD商业软件，建立风口回旋区三维模型，针对氧气高炉所设计的新型燃烧器中氧煤枪数量及其与直吹管所呈角度和空间物理位置对风口回旋区流场的影响进行数值模拟。研究结果表明：采用单支氧煤枪操作，当其位于直吹管上部时，煤气流速度随喷吹角度由7°~15°变化时逐渐减小，且夹角为9°较为适宜，当其位于下部时，随着夹角越大，对风口回旋区深度增加越有利；采用双氧煤枪操作，当其在直吹管上下、左右分布时，夹角分别为11°和13°较合理；当单支氧煤枪位于直吹管上方且夹角为9°、距离d为75 mm时能较好地促进风口回旋区深度增加并保持足够的鼓风动能。

关键词：氧气高炉；氧煤燃烧器；设计参数；风口回旋区；数值模拟

中图分类号：TF512          文献标志码：A         文章编号：1672-7207(2016)05-1480-07

Numerical analysis of flow behavior in tuyere and raceway of oxygen blast furnace with new type of oxy-coal burner

ZHANG Chao, ZHANG Jianliang, SUN Hui, LIU Zhengjian

 (School of Metallurgical and Ecological Engineering, University of Science and Technology Beijing,

Beijing 100083, China)

Abstract: Oxygen blast furnace can effectively reduce CO₂ emissions by two means, pulverized coal injection and recycling of CO₂-removed blast furnace gas. To study the velocity field among the tuyere and raceway region, a three-dimensional model was build up using the commercial CFD software. The factors these numerical simulations mainly focus on the number of oxygen-coal lances, the angle and distance between the blowpipe and oxy-coal lances. Numerical results show that increasing angle between the blowpipe and oxy-coal lance from 7° to 15° results in lower velocity when the oxy-coal lance is set above the blowpipe, the appropriate angle is 9°. When the lance is located below the blowpipe, the bigger the angle is, the deeper the raceway will be. In addition, when the oxy-coal burner has two lances, the lances are set at two sides of the blowpipe, i.e. vertical and horizontal distribution around the blowpipe, and the reasonable angles are 11° and 13°. Besides, the suitable distance between the blowpipe and oxy-coal lance is 75 mm when the oxy-coal lance is set above the blowpipe.

Key words: oxygen blast furnace; oxy-coal burner; design parameters; raceway; numerical simulation

氧气高炉炼铁技术是可实现规模化应用的炼铁新工艺之一^[1]。该工艺采用氧气鼓风，大量喷吹煤粉，并将炉顶煤气经脱除CO₂处理后喷入高炉以达到循环利用的目的。在高炉炼铁过程中，风口回旋区对高炉能否保持平稳操作和顺行具有重要意义，然而，回旋区在高炉中的形状和尺寸很难通过实验直接获得^[2]，因此，数值模拟成为一种获取风口回旋区信息的重要手段。利用CFD商业软件对高炉风口回旋区的流场进行数值模拟研究，具有成本低、速度快且可以模拟真实条件及理想条件等优点，目前已在风口回旋区的研究中得到广泛应用^[3-5]。郭同来等^[6]建立了高炉喷吹焦炉煤气风口回旋区数学模型，系统研究了焦炉煤气喷吹量对风口理论燃烧温度、炉腹煤气量和回旋区形状的影响。SHEN等^[7-9]通过一系列数值模拟，探究了喷吹煤粉颗粒在风口区域的脱挥发分和燃烧行为。WIJAYANTA等^[10]研究了喷吹生物质焦对回旋区的影响。储满生等^[11]运用数值模拟的方法研究了喷吹含氢物质对高炉风口的影响。SHEN等^[12-13]建立了回旋区形状的3-D模型，讨论了煤粉成分、焦炭孔隙度等因素对煤粉和焦炭在风口回旋区的燃烧行为。RAJNEESH等^[14-15]也建立了预测风口回旋区尺寸的二维数学模型。上述风口回旋区数值模拟研究大都是基于传统氧煤枪插入方式进行的。在此方式下，氧煤枪斜插入直吹管内，喷入煤粉并由热风带入回旋区^[16]。对于氧气高炉，直吹管内喷吹的气体是脱除CO₂后的炉顶循环煤气，含有较高的CO，而传统方式往往导致燃烧前沿向风口方向移动，易发生爆炸，故采用新型方式。新型燃烧器设计下氧煤枪呈同轴套筒式结构，外环通入氧气，内部运送煤粉，而且氧煤枪与直吹管并行插入风口小套，依靠风口小套内循环水进行冷却。本文作者研究基于新型氧煤燃烧器设计，建立氧气高炉风口回旋区的3-D模型，对氧煤枪数量、与直吹管所呈角度及空间位置对风口回旋区流场的影响进行数值模拟，以探究合理的布置参数。

1  物理模型

图1所示为传统方式与新型方式下氧煤燃烧器布置方式示意图。由图1可知：较传统方式而言，新型方式有利于氧煤枪枪头冷却，延长其使用寿命。且煤粉燃烧火焰焦点更趋于回旋区内，降低了直吹管与风口小套内温度。

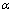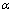图2所示为风口回旋区3-D模型示意图。由图2可见：该模型由直吹管、风口、氧煤枪、高炉回旋区及其周围的焦炭层组成。图中：D_r和H_r分别为回旋区的深度和高度；为焦炭层孔隙度；d为氧煤枪出口中点和直吹管中心线之间的距离；为氧煤枪和直吹管中心线所呈夹角。为根据高炉生产实际情况，定义回旋区为空腔，设定焦炭层为多孔介质，孔隙度=0.5^[14]。

图1  氧煤燃烧器示意图

Fig. 1  Diagram of oxygen-coal burner configurations

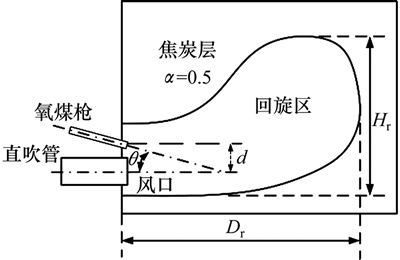
图2  物理模型尺寸参数示意图

Fig. 2  Diagram of geometry and computational domain used in numerical simulation

目前，高炉研究者提出了很多预测风口回旋区大小的模型，本文中，风口回旋区的形状尺寸计算则采用了修正后的Hatano模型(详见附件)。该模型综合考虑了鼓风穿透力、焦炭自身重力以及壁面的反作用力等因素，得到了回旋区深度、宽度和高度的计算模型。不同的操作参数会导致不同的回旋区尺寸^[17-18]，为研究氧煤燃烧器参数对回旋区的影响，必须保证其他参数不变，意味着模拟中回旋区的形状是确定的。根据氧气高炉设计要求及模型计算，确定风口回旋区深度为512 mm，高度为437 mm及宽度为284 mm。

2  数学模型

采用Fluent 6.3对风口回旋区流场进行数值模拟，研究氧煤枪数量、空间位置以及直吹管-氧煤枪角度对回旋区流场的影响。流场特征用三维稳态Navier-Stokes方程来计算表征。

2.1  湍流模型

考虑到湍流模型稳定性以及模拟普适性精度问题，采用k-ε标准双方程来封闭方程组。模型中对应湍动能k方程和对应湍动能扩散系数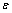方程描述如下：

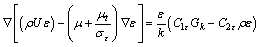
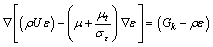
式中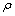：为气体密度，kg/m³；k为湍流动能，m²/s²；C_μ，C_1ε和C_2ε为标准k-ε湍流模型经验常数；ε为湍动能耗散率，m²/s²；G_k为平均速度梯度产生的湍流动能；σ_k和σ_ε为湍流动能普朗特数；μ为动力黏度，Pa/s；μ_t为湍流黏度，kg/(m·s)；U为主流速度，m/s；C_μ=0.09，σ_k=1.0，σ_ε=1.3，C_1ε=1.44，C_2ε=1.92^[19]。

2.2  求解方案

为研究氧煤枪数量、空间位置以及直吹管-氧煤枪角度对回旋区流场的影响，制定2种数值计算方案，如表1和2所示。由于氧煤枪有一定长度，考虑到实际生产现场氧煤枪布置的空间因素，氧煤枪中心线与直吹管中心线夹角θ设计范围为7°~15°。

2.3  边界条件

模拟区域为包括整个风口回旋区的焦炭层，长度、高度和宽度分别为600，500和350 mm。根据氧煤枪与直吹管的直径比，直吹管直径取45 mm，氧煤枪内氧气通道等效直径取16 mm，直吹管和氧煤枪自由湍流强度均为10%，直吹管内喷吹循环煤气，速度为197 m/s，氧煤枪喷吹氧气流速为235 m/s。出口条件为压力出口，水力直径分别为0.412 m和0.442 m，另设墙体边界条件为速度无滑移，采用非结构化网格，总数量约为690 000个。压力耦合算法采用缺省格式，为降低计算发散性，空间离散对流项各控制方程均采用二阶迎风格式。由于回旋区内高度旋流作用，且有多孔焦炭层，存在压力突变，故分离算法采用PRESTO!。

表1  数值计算方案1

Table 1  Calculation program 1

表2  数值计算方案2

Table 2  Calculation program 2

3  结果与讨论

本研究中，因炉内测量技术不足，模型无法通过工业实际测量进行验证。对普通高炉回旋区，国内外一些学者进行了相关研究。本文将模拟结果和SHEN等^{[12, 20-21]}所建立的模型进行对比，上述模型是通过离散化颗粒的方法对风口回旋区进行仿真计算。对比发现本文模拟结果与文献所得流场，其趋势无论在回旋区边界还是内部都相吻合，证明本文模型结果可靠。

本文探讨了燃烧器设计参数对回旋区速度场的影响。速度越大，煤气流对焦炭颗粒的裹挟能力就越大，对焦炭层的冲刷越为猛烈，从而使得实际形成的回旋区深度也会增大。图3所示为风口回旋区内速度场云图。从图3可以看出：循环煤气主要由风口回旋区末端上部溢出，因此，回旋区深度越大，越有利于中心煤气流的发展，故选取风口中心线煤气流速度作为回旋区流场表征因素。

图3  风口回旋区速度场云图

Fig. 3  Contour of raceway velocity field

3.1  单枪布置方式对回旋区流场的影响

单支氧煤枪喷吹作用下，氧气流对回旋区流场的影响较为一致，即距风口距离的增加，速度首先在较短范围内呈缓慢衰减，然后加速衰减到达回旋区边界。进入风口初始阶段，气体速度衰减缓慢，这是煤气湍流尚未充分发展造成的。当其到达回旋区边缘后，接触焦炭层，前进阻力陡然增加，从而导致速度加速   衰减。

图4所示为单支氧煤枪在直吹管上部、不同角度θ下沿风口中心线流场速度分布。由图4可知：随着喷吹角度增大，中心线同一位置处速度逐渐减小。这是因为随角度增大，氧煤枪所喷吹氧气流对回旋区气流的回旋作用产生阻隔，且产生阻力逐渐变大。由于煤粉燃烧主要发生在风口附近^[16]，此时，煤粉与气体混合状况对燃烧促进作用较显著。由图4可看出：气体进入风口初始阶段，特别是氧煤枪与直吹管夹角

为9°的情况下，气流速度较快，有利于煤粉与气体充分混合，可以促进煤粉燃烧；当进入回旋区后，煤气流速衰减较慢，因此，在此角度下，较有利于煤粉燃烧和风口回旋区深度增加。

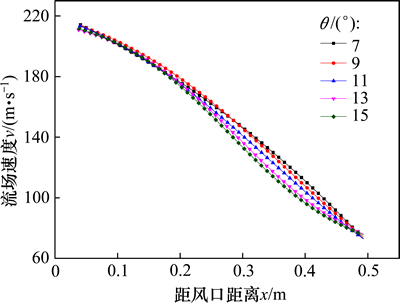
图4  单枪在上时不同θ下风口区流场

Fig. 4  Velocity distribution at different angles with lance above blowpipe

图5所示为单支氧煤枪在直吹管下部不同角度θ下流场速度沿着风口中心线的分布。由图5可知：随着到风口距离的增加，速度变化与单支氧煤枪在直吹管上部时规律相同。不同之处在于：随喷吹角度增大，风口中心线上同一点速度逐渐增大，且增大幅度较氧煤枪位于直吹管上部时小。由此说明由氧煤枪中喷出的气流对直吹管的气流具有支撑作用。这是因为回旋区内气流逆时针旋转，当枪体位于下部时，氧气流向上倾斜角度越大，其对煤气回旋的促进作用越明显。因此，当氧煤枪位于直吹管上部时，夹角越大，越有利于回旋区深度增加。

由图4和5可知：当氧煤枪在位于直吹管上部时，随着角度θ增加，可引起速度波动，约16 m/s；而当氧煤枪位于下部时，速度变化约为10 m/s。这说明当角度变化值相同时，氧煤枪位于直吹管上部时造成的阻力作用对速度场的影响要大于其位于下部时产生的促进作用的影响。

图5  单枪在下时不同θ下风口区流场

Fig. 5  Velocity distribution at different angles with lance below blowpipe

当氧煤枪位于上部，煤气流到达回旋区末端时，不同角度下速度趋于一致；当氧煤枪位于下部，煤气流在距离风口0.4 m时，不同角度下速度区别不太明显。由此说明：当氧煤枪位于直吹管下部时，有助于风口煤气流速的稳定。

3.2  双枪布置方式对风口区流场的影响

当采用双氧煤枪时，其中心线与风口中心线之间形成紊乱的流场区域。进入风口的煤气流，不仅在直吹管上部形成气流回旋，在直吹管两侧同样存在气流回旋，说明煤气流的回旋是立体的。

图6所示为双氧煤枪在直吹管上、下侧布置时不同角度对风口区流场的影响。由图6可见：沿着风口中心线距离增加，速度衰减规律与单支氧煤枪情况下相同，但不同角度之间，速度差值最大值仅为4 m/s，无明显差别。这是因为：对于单支氧煤枪，当其位于上部时，角度越小，同一位置下速度越大；当氧煤枪位于下部时角度越小，则同一位置下速度越小；当氧煤枪上、下2支布置时，两者的作用相互抵消，使得角度变化对速度场的影响程度较单支氧煤枪下不够明显。然而，当距风口0.25 m前，各角度下速度区别不明显，当距风口距离大于0.25 m后，速度差异变大。考虑到回旋区内速度对其深度产生影响，角度为11°时速度较其他值大，且衰减程度较小，故在此角度下对风口区扩大及延伸最为有利。

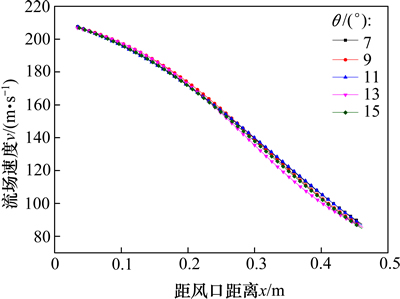
图6  双枪上下布置时不同θ下风口区流场

Fig. 6  Velocity distribution at different angles with lances vertical distribution

图7所示为双氧煤枪在直吹管左、右侧布置时不同角度对风口回旋区流场的影响。从图7可知：随喷吹角度增大，风口中心线上同一位置处速度逐渐变大，速度增加幅度为10 m/s。这是因为左右氧煤枪喷吹氧气流时角度越大，对煤气流回旋中心的形成越有利。综合考虑进入风口区初始阶段气流速度对煤粉、气体的混合效果以及回旋区的吹透深度影响，氧煤枪与直吹管夹角为13°时最为合理。

图8所示为不同角度下，不同氧煤枪布置方式对风口回旋区流场的影响。由图8可知：对于单支氧煤枪，当角度处于7°~11°范围内，沿风口中心线，枪体位于直吹管上部比位于下部时速度要大。在13°~15°

范围内，直吹管上部所对应的速度比下部时小。当氧煤枪在直吹管上部时，角度较小时，从氧煤枪中喷出的氧气流可以促进回旋煤气流形成中心漩涡，此时将有利于减少煤气推进过程中阻力。而随着角度增大，氧气流对直吹管喷吹的循环煤气流形成冲击，阻碍了其回旋过程流线的自由延伸。当氧煤枪位于下部时，氧气流向上倾斜的角度对循环煤气回旋产生促进作用，且随着角度增大而增强。在上述2种状况综合作用下，使得角度θ超过11°时，氧煤枪位于上部时的循环煤气速度低于其位于下部时的情况。

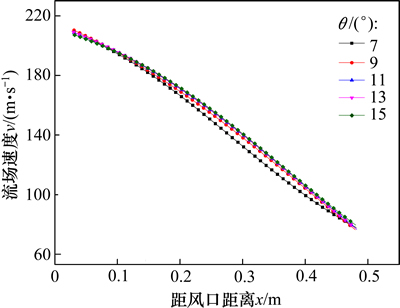
图7  双枪左右布置时不同θ下风口区流场

Fig. 7  Velocity distribution at different angles with lances horizontal distribution

对于双氧煤枪情况，在计算角度范围内，氧煤枪上下布置时，其沿中心线的速度处于2种单枪之间。当角度处于7°~11°范围时，氧煤枪上下布置比左右布置的速度衰减慢。当角度超过13°后，氧煤枪上下布置则比左右布置速度衰减快。

3.3  氧煤枪与直吹管距离对风口区流场的影响

图9所示为固定氧煤枪与直吹管角度下，研究氧煤枪中心线与直吹管中心线距离d对风口回旋区流场的影响，其中设定夹角为9°。由图9可知：当距风口距离不大于0.25 m时，随着距离d增加，风口中心线上速度变化不明显，因此，在不同距离d下接近风口处速度变化较小，对煤粉混合燃烧影响也较小。然而，当距风口距离大于0.25 m时，速度场波动较大，这主要是氧煤枪内氧气流及回旋区逆向回旋气流对风口中心线上循环煤气的综合作用造成的。由图9可见：当距离d为75 mm时，对于促进风口回旋区深度增加而保持足够的鼓风动能及确保设备安装节约原则最为 合理。

图8  相同角度不同氧煤枪布置方式下风口区流场

Fig. 8  Velocity distribution at different lances configurations with the same angle

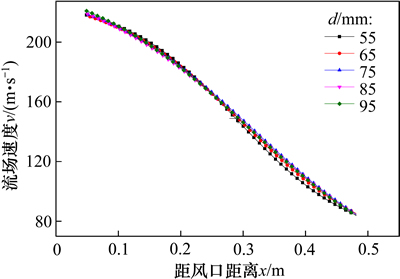
图9  氧煤枪与直吹管距离对风口区的影响

Fig. 9  Velocity distribution at differents distance between lance and blowpipe

4  结论

1) 单支氧煤枪位于直吹管上部时，在所模拟角度范围内，随喷吹角度的逐渐增大，煤气流速度逐渐减小，且在所模拟的具体条件下，取夹角为9°时较为适宜；单支氧煤枪位于直吹管下部时，夹角越大，越有利于风口回旋区深度增加。

2) 当双氧煤枪在直吹管上下分布时，速度场介于2种单支氧煤枪形式之间，且夹角为11°时较为合理；当氧煤枪位于直吹管左右时，夹角为13°较有利于回旋中心形成。

3) 固定单支氧煤枪位于直吹管上方且夹角为9°，当距离d为75 mm时，对于促进风口回旋区深度增加而保持足够的鼓风动能最为合理。

参考文献：

[1] JIANWEI Y, GUOLONG S, CUNJIANG K, et al. Oxygen blast furnace and combined cycle (OBF-CC): an efficient iron-making and power generation process[J]. Energy, 2003, 28(8): 825-835.

[2] BABICH A, SENK D, FERNANDEZ M. Charcoal behaviour by its injection into the modern blast furnace[J]. ISIJ International, 2010, 50(1): 81-88.

[3] NOGAMI H, KASHIWAYA Y, YAMADA D. Simulation of blast furnace operation with intensive hydrogen injection[J]. ISIJ International, 2012, 52(8): 1523-1527.

[4] DE CASTRO J A, G D M, DA MOTA I D O, et al. Analysis of the combined injection of pulverized coal and charcoal into large blast furnaces[J]. Journal of Materials Research and Technology, 2013, 2(4): 308-314.

[5] ROCHA E P D, GUILHERME V S, CASTRO J A D, et al. Analysis of synthetic natural gas injection into charcoal blast furnace[J]. Journal of Materials Research and Technology, 2013, 2(3): 255-262.

[6] 郭同来, 柳政根, 储满生. 高炉喷吹焦炉煤气风口回旋区的数学模拟[J]. 东北大学学报(自然科学版), 2012, 33(7): 987-991.

GUO Tonglai, LIU Zhenggen, CHU Mansheng. Numerical simulation of blast furnace raceway with coke oven gas injection[J]. Journal of Northeastern University (Natural Science), 2012, 33(7): 987-991.

[7] SHEN Y S, GUO B Y, YU A B, et al. Three-dimensional modelling of coal combustion in blast furnace[J]. Iron and Steel Institute of Japan, 2008, 48(6): 777-786.

[8] SHEN Y S, GUO B Y, YU A B, et al. Model study of the effects of coal properties and blast conditions on pulverized coal combustion[J]. Iron and Steel Institute of Japan, 2009, 49(6): 819-826.

[9] SHEN Y S, GUO B Y, YU A B, et al. A three-dimensional numerical study of the combustion of coal blends in blast furnace[J]. Fuel, 2009, 88(2): 255-263.

[10] WIJAYANTA A T, ALAM M S, NAKASO K, et al. Combustibility of biochar injected into the raceway of a blast furnace[J]. Fuel Processing Technology, 2014, 117(0): 53-59.

[11] CHU M, NOGAMI H, YAGI J I. Numerical analysis on injection of hydrogen bearing materials into blast furnace[J]. ISIJ International, 2004, 44(5): 801-808.

[12] SHEN Y S, YU A B, AUSTIN P R, et al. CFD study of in-furnace phenomena of pulverised coal injection in blast furnace: effects of operating conditions[J]. Powder Technology, 2012, 223(6): 27-38.

[13] SHEN Y S, YU A B, AUSTIN P R, et al. Modelling in-furnace phenomena of pulverized coal injection in ironmaking blast furnace: Effect of coke bed porosities[J]. Minerals Engineering, 2012, 33: 54-65.

[14] RAJNEESH S, SARKAR S, GUPTA G S. Prediction of raceway size in blast furnace from two dimensional experimental correlations[J]. Iron and Steel Institute of Japan, 2004, 44(8): 1298-1307.

[15] SARKAR S, GUPTA G S, LITSTER J D, et al. A cold model study of raceway hysteresis[J]. Metallurgical and Materials Transactions B, 2003, 34(2): 183-191.

[16] YEH C P, DU S W, TSAI C H, et al. Numerical analysis of flow and combustion behavior in tuyere and raceway of blast furnace fueled with pulverized coal and recycled top gas[J]. Energy, 2012, 42(1): 233-240.

[17] NOGAMI H, YAMAOKA H, TAKATANI K. Raceway design for the innovative blast furnace[J]. Iron and Steel Institute of Japan, 2004, 44(12): 2150-2158.

[18] RANGARAJAN D, SHIOZAWA T, SHEN Y, et al. Influence of operating parameters on raceway properties in a model blast furnace using a two-fluid model[J]. Industrial & Engineering Chemistry Research, 2014, 53(13): 4983-4990.

[19] LAUNDER B E, SPALDING D B. The numerical computation of turbulent flows[J]. Computer Methods in Applied Mechanics and Engineering, 1974, 3(2): 269-289.

[20] TRUELOVE J S, HOLCOMBE D. Measurement and modelling of coal flame stability in a pilot-scale combustor[J]. Symposium (International) on Combustion, 1991, 23(1): 963-971.

[21] ZHOU Z Y, ZHU H P, YU A B, et al. Discrete particle simulation of gas-solid flow in a blast furnace[J]. Computers & Chemical Engineering, 2008, 32(8): 1760-1772.

(编辑  陈爱华)

收稿日期：2015-05-13；修回日期：2015-07-05

基金项目(Foundation item)：国家自然科学基金委员会与宝钢集团有限公司联合资助项目(51134008)；国家重点研究发展计划(973计划)资助项目(2012CB720401) (Project(51134008) supported by the National Natural Science Foundation of China and Baosteel Group Corporation; Project(2012CB720401) supported by the National Key Research and Development Program (973 Program) of China)

通信作者：张建良，教授，博士生导师，从事炼铁新技术研究；E-mail: jl.zhang@ustb.edu.cn