
Effect of external stress on phase diagrams and dielectric properties of epitaxial ferroelectric thin films grown on orthorhombic substrates
L? Ye-gang(吕业刚)1, DENG Shui-feng(邓水凤)1, 2, GONG Lun-jun(龚伦军)1, 2, YANG Jian-tao(杨建桃)1
1. Faculty of Material and Photoelectronic Physics, Xiangtan University, Xiangtan 411105, China;
2. Key Laboratory for Advanced Materials and Rheological Properties, Ministry of Education,
Xiangtan University, Xiangtan 411105, China
Received 10 April 2006; accepted 25 April 2006
Abstract: A Landau-Ginsburg-Devonshire(LD)-type thermodynamic theory was used to describe the effect of external stress on phase diagrams and dielectric properties of epitaxial ferroelectric thin films grown on orthorhombic substrates which induce nonequally biaxial misfit strains in the films plane. The “misfit strain-external stress” and “external stress-temperature” phase diagrams were constructed for single-domain BaTiO3(BT) and PbTiO3(PT) thin films. It is shown that the external stress may lead to the rotation of the spontaneous polarization and a gradual change of its magnitude, which may result in phase transition. Nonequally biaxial misfit strains dependence of the stability of polarization states may be governed by external stress. At room temperature, stress-induced ferroelectric/paraelectric phase transition which occurs in film on cubic substrate does not take place in the ferroelectric thin film grown on orthorhombic substrate. It is also shown that the nonequally misfit strains in the film plane may lead to the appearance of new phases which do not form in films grown on cubic substrates under external stress. The dependence of the dielectric response on the external stress is also studied. It is shown that the dielectric constants of single-domain PT and BT films are very sensitive to the external stress under the given anisotropic misfit strains-temperature conditions. It presents theoretical evidence that the external stress and anisotropic misfit strains can be employed for improving the thin films physical properties.
Key words: external stress; phase transition; dielectric constant; orthorhombic substrate; misfit strain
1 Introduction
Ferroelectric thin films have been widely investigated in recent years. Not only the ferroelectric, dielectric, and piezoelectric properties were found to be promising for microelectric and micromechanical applications[1], but also the physical properties of ferroelectric thin films were found to be substantially different from those of bulk ferroelectrics[2,3]. These differences are partly due to the straining and two- dimensional clamping of the film by a dissimilar thick substrate[4]. The misfit strains between a ferroelectric thin film and its substrate are able to change the Curie’s temperature, the order of the paraelectric/ferroelectric phase transition, the equilibrium polarization states, and the dielectric properties of the material[5]. The relationship between the misfit strains and the material properties has been theoretically analyzed by thermodynamic formalism on the basis of the Landau- Devonshire phenomenological theory[6-10] and experimentally investigated by changing the substrate [11, 12]. However, most of the work has investigated only equally biaxial misfit strains which are induced into ferroelectric thin films grown on the cubic substrates. The orthorhombic substrate induces nonequally biaxial misfit strains which lead to new material properties and provide the possibilities for the design of electronic devices[13-15].
In the previous studies on orthorhombic substrate, it was assumed that there are no external mechanical forces acting on the upper surface of the film. However, experimental studies of the direct piezoelectric effect require an external loading of the free surface[16]. When the scanning force microscopy(SFM) piezoresponse imaging method and the microindentation of ferroelectric thin films were used to study the properties of thin films, they could produce a force pressing the tip to the film surface[17, 18]. Therefore, it is necessary to use a theory to investigate the effect of the external force on physical properties of thin films. In this paper, a nonlinear thermodynamic theory is developed for uniformly loaded single-domain ferroelectric thin films grown on orthorhombic substrates. The phase diagrams and dielectric properties of epitaxial ferroelectric thin films are investigated by a LD-type thermodynamic theory. It is shown that the external stress may induce phase transition and dielectric anomaly even at room temperature. Therefore, it presents better understanding of the ferroelectric behavior of loaded epitaxial films grown on orthorhombic substrates, and provides a quantitative theoretical estimation to serve as a guide for the experimental future studies.
2 Thermodynamics of single-domain ferro- electric thin films
Considering a single-domain ferroelectric thin film grown on a thick orthorhombic substrate, it is assumed that the film/substrate interface is coherent[13]. The orthorhombic substrate induces nonequally biaxial in-plane misfit strains (e1, e2) and a shear deformation e6 in the film. We use the Voigt matrix notation of strains and the rectangular Cartesian frame of reference with the x3 axis perpendicular to the film/substrate interface. The lattice matching between the film and a thick orthorhombic substrate implies that the in-plane strains e1, e2 and shear deformation e6 of the film at the film/substrate interface are totally controlled by the substrate which is assumed to be sufficiently thick[14]. They can be considered fixed parameters of the film/substrate system. The misfit strains can be defined as e1=(b-a0)/b, e2=(c-a0)/c, where b and c are the in-plane substrate lattice parameters and a0 is the lattice constant of the cubic paraelectric phase of the film at the stress-free state. The shear strain e6 is approximately zero because the plane stress condition is held along the film thickness direction due to the thin thickness of the film[13]. Using the standard elastic Gibbs function G[5], the equilibrium thermodynamic potential 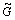 of ferroelectric film can be derived by the relation
of ferroelectric film can be derived by the relation 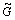 =G+e1σ1+e2σ2. The stress σ3 will be regarded as a given external stress, whereas the shear stress σ4 and σ5 will be neglected[5]. The stresses σ1, σ2 and σ6 can be calculated using the relations ei=-?G/?σi, which describes the elastic equation of state of a ferroelectric crystal[19]. Substituting of these relations into the basic formula for the modified thermodynamic potential, the expression for
=G+e1σ1+e2σ2. The stress σ3 will be regarded as a given external stress, whereas the shear stress σ4 and σ5 will be neglected[5]. The stresses σ1, σ2 and σ6 can be calculated using the relations ei=-?G/?σi, which describes the elastic equation of state of a ferroelectric crystal[19]. Substituting of these relations into the basic formula for the modified thermodynamic potential, the expression for 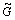 can be obtained:
can be obtained:
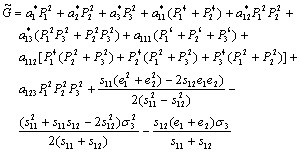 (1)
(1)
where
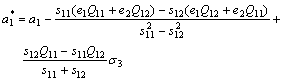 (2)
(2)
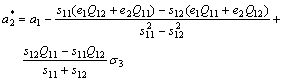 (3)
(3)
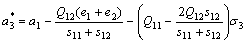 (4)
(4)
a1 is the dielectric stiffness, aij and aijk are higher-order stiffness coefficients at constant stress, Qij are the electrostrictive coefficients, sij are the elastic compliances at constant polarization, and 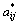 are the renormalized coefficients[5].
are the renormalized coefficients[5].
From Eqn.(1), it is possible to calculate all minima of the film thermodynamic potential corresponding to polarization states of film, since the modified potential 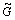 is a function of polarization components Pi (i=1, 2, 3). Eqns.(2)-(4) indicates that the renormalized coefficients
is a function of polarization components Pi (i=1, 2, 3). Eqns.(2)-(4) indicates that the renormalized coefficients 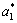 ,
, 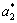 and
and 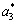 are linear functions of the misfit strains e1, e2 and external stress σ3. The spontaneous polarization ps may change with the misfit strains e1, e2 and external stress σ3 in the film/substrate system. The temperature dependence of ferroelectricity is mainly governed by the dielectric stiffness a1=(T-θ)/2ε0C, since the high-order stiffness coefficients aij and aijk may be taken as temperature-independent parameters. Here, θ and C are the Curie-Weiss temperature and constant, and ε0 is the permittivity of the vacuum[20].
are linear functions of the misfit strains e1, e2 and external stress σ3. The spontaneous polarization ps may change with the misfit strains e1, e2 and external stress σ3 in the film/substrate system. The temperature dependence of ferroelectricity is mainly governed by the dielectric stiffness a1=(T-θ)/2ε0C, since the high-order stiffness coefficients aij and aijk may be taken as temperature-independent parameters. Here, θ and C are the Curie-Weiss temperature and constant, and ε0 is the permittivity of the vacuum[20].
3 Phase diagrams of single-domain BaTiO3 and PbTiO3 epitaxial films on orthorhom- bic substrate
The misfit strain-external stress and external stress-temperature phase diagrams can be constructed for single-domain BaTiO3(BT) and PbTiO3(PT) thin films grown on orthorhombic substrates. The possible phases which may appear in the films grown on orthorhombic substrates involve: 1) the paraelectric phase (p-phase), where P1=0, P2 =0, and P3=0; 2) a1-phase, where P1≠0, P2=0, and P3=0; 3) a2-phase, where P1=0, P2≠0, and P3=0; 4) c-phase, where P1=0, P2=0, and P3≠0; 5) a1c-phase, where P1≠0, P2=0, and P3≠0; 6) a2c-phase, where P1=0, P2≠0, and P3≠0; 7) a12-phase, where P1≠0, P2≠0, and P3=0; 8) r-phase, where P1≠0, P2≠0, and P3≠0. Using numerical calculation method with the values of the involved materials parameters[5], we obtain all minima of the modified potential 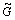 with respect to polarization components for every possible phase. Then selecting the energetically most favorable thermo- dynamic state for each point of the misfit strain-external stress plane, we obtain the equilibrium phase diagrams of BT and PT epitaxial films at room temperature. We fix e1=0.005, so that the phase diagrams can be constructed in two-dimensional plane using misfit strain e2 and external stress σ3 as two independent variables.
with respect to polarization components for every possible phase. Then selecting the energetically most favorable thermo- dynamic state for each point of the misfit strain-external stress plane, we obtain the equilibrium phase diagrams of BT and PT epitaxial films at room temperature. We fix e1=0.005, so that the phase diagrams can be constructed in two-dimensional plane using misfit strain e2 and external stress σ3 as two independent variables.
Fig.1 shows the misfit strain—external stress phase diagrams of single-domain BT and PT epitaxial thin films respectively. It is shown that the external stress may lead to phase transition in single-domain BT and PT thin films at room temperature. The external tensile stress favors the formation of c-phase with polarization pointing to out-of-plane, while the large compressive stress stabilizes in-plane tetragonal phase. There are agreement with the experimental result and may be explained for the reorientation of the domains induced by external stress[21]. The phase diagrams of thin films grown on orthorhombic substrates are substantially different from that of films on cubic substrates. It is shown that the external stress and nonequally biaxial misfit strains may lead to the appearance of new phases which do not form in films grown on cubic substrates. These are tetragonal phases (a1, a2), orthorhombic phases (a1c, a2c, a12), and the triclinic r-phase. In tetragonal phases (a1, a2), the spontaneous polarization ps is oriented along one of the in-plane edges of the prototypic unit cell. In orthorhombic phases (a1c, a2c), ps has both in-plane and out-of-plane nonzero components. In the triclinic r-phase, ps is rotated away from the diagonal of the unit cell. The stabilities of these new ferroelectric phases depend on the external stress and misfit strains. EMELYANOV et al[4] predicted that the compressive stress-induced ferroelectric/paraelectric phase transition may take place in ferroelectric thin films grown on cubic substrates even at temperatures well below the Curie’s temperature of the bulk material. However, the transition is forbidden in the thin films grown on orthorhombic substrates. Compared with the cubic substrate, the orthorhombic substrate exhibits sufficiently different properties in the epitaxial ferroelectric thin films. It may provide the possibilities for the design of new electronic devices by changing the cubic substrate into the orthorhombic one.
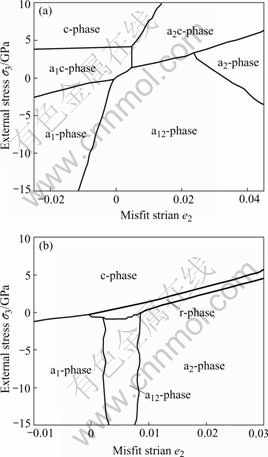
Fig.1 Misfit strain—external stress phase diagrams of single- domain BT (a) and PT (b) thin films grown on orthorhombic substrates (One of in-plane misfit strains e1 is fixed to 0.005 and temperature is taken to be 25 ℃. The thin and thick lines denote the second- and first-order phase transition boundaries, respectively.)
In order to investigate the effect of external stress on phase transition at different temperatures, the external stress—temperature phase diagrams are constructed for BT and PT epitaxial thin films. We choose the orthorhombic substrate with misfit strains e1=0.005, e2= -0.005 for BT epitaxial film and that with e1=0.005, e2= 0.01 for PT epitaxial film. Fig.2 shows the external stress—temperature phase diagrams for BT and PT epitaxial films respectively. It is shown that the external stress does not change the order of the paraelectric/ ferroelectric phase transition, which remains of the second order as in unloaded single-domain films[5]. From Fig.2(a), the paraelectric/ferroelectric phase transition temperature increases with the magnitude of compressive stress and varies nonmonotonically with tensile stress in BT film. From Fig.2(b), it is seen that the ferroelectric transition temperature increases with the external compressive stress. The a2/c-phase, a2/r-phase, r/c-phase transitions are of the first order, since the polarization components are discontinuous at the phase boundaries[13].
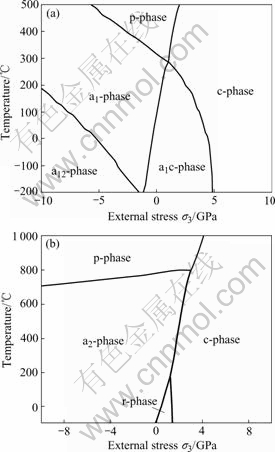
Fig.2 External stress—temperature phase diagrams of single- domain BT (a) and PT (b) thin films grown on given orthorhombic substrates at 25 ℃ (The in-plane biaxial misfit strain e1 is fixed to be 0.005 in both films. The misfit strains e2 are taken to be -0.005 and 0.01, which correspond to the orthorhombic substrates of BT and PT epitaxial films respectively. The thin and thick lines denote the second- and first-order phase transition boundaries, respectively.)
4 Dielectric responses of single-domain BaTiO3 and PbTiO3 epitaxial films
The effect of external stress on the dielectric response is discussed, since the stress-induced phase transitions may be accompanied by dielectric anomaly. By differentiating the modified thermodynamic potential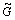 , we can obtain explicit expressions for the reciprocal dielectric susceptibilities
, we can obtain explicit expressions for the reciprocal dielectric susceptibilities 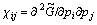 . The matrix χij inversion enables us to obtain the dielectric susceptibilities
. The matrix χij inversion enables us to obtain the dielectric susceptibilities  The dielectric constants can be derived from the relation εij=ε0+ηij. Therefore, the dielectric constants εij of epitaxial ferroelectric films are a function of the nonequally biaxial misfit strains, temperature, and external stress.
The dielectric constants can be derived from the relation εij=ε0+ηij. Therefore, the dielectric constants εij of epitaxial ferroelectric films are a function of the nonequally biaxial misfit strains, temperature, and external stress.
Figs.3(a) and (b) show the variations of the diagonal components εii (i=1, 2, 3) of the dielectric tensor with the external stress at room temperature. It can be seen that the film dielectric constants vary nonmonotonically with the external stress in the epitaxial film system. From Fig.3(a), the dielectric constants ε11, ε22 and ε33 are very large values at which the stresses close to -5.5, -0.15 and 4.5 GPa, corresponding to the second-order a12/a1-phase, a1/a1c-phase, and a1c/c-phase transitions taking place respectively. The reduction of the magnitude of stress may lead to the increase of dielectric constants ε11, ε22 and ε33 in the a12-phase and c-phase. From Fig.3(b), the dielectric constant ε11 is thundering large value in the a2-phase. The first-order r/c-phase transition, at which the stress closes to 1.2 GPa, is accompanied by a step-like increase of the dielectric constants ε11, ε33. In the c-phase, the dielectric constants ε11, ε22 increase with the decrease of tensile stress. Therefore, applying an appropriate external stress to the film surface, we can approve its dielectric properties.

Fig.3 Dependence of dielectric constants of single-domain BT (a) and PT (b) thin films on external stress at 25℃ (The in-plane biaxial misfit strain e1 is fixed to be 0.005 in both films. The misfit strains e2 are taken to be -0.005 and 0.01, which correspond to the orthorhombic substrates of BT and PT epitaxial films respectively. The inset in (b) shows that the dielectric constant  reaches thundering large value in the a2-phase.)
reaches thundering large value in the a2-phase.)
5 Conclusions
The nonlinear thermodynamic theory is developed to explain the effect of external stress on the phase diagrams and dielectric properties in ferroelectric thin films grown on the orthorhombic substrates. It is shown that the external stress may lead to the rotation of the spontaneous polarization ps and a gradual change of its magnitude, which may result in phase transition. The paraelectric/ferroelectric phase transition temperature varies nonmonotonically with the external stress. In contrast with the cubic substrate, the orthorhombic substrate with the nonequally biaxial misfit strains restrains the phase transition from the ferroelectric phase to paraelectric one at temperatures well below the Curie temperature of the bulk material (e.g. at room temperature). It may provide the possibilities for the design of new electronic devices by changing the cubic substrate into the orthorhombic one. The anisotropic misfit strains may lead to appearance of the new phases. It is shown that the different phases exhibit distinct physical properties. The dielectric constant may be very large value at which the phase transition takes place. External stress may lead to dramatical increase of the dielectric constant. Therefore, it opens an effective way to improve the dielectric response by applying an appropriate external stress to the film.
References
[1] SCOTT J F. Device physics of ferroelectric memories [J]. Ferroelectrics, 1996, 183: 51-63.
[2] ZHENG X J, LI J Y, ZHOU Y C. X-ray diffraction measurement of residual stress in PZT thin films prepared by pulsed laser deposition [J]. Acta Mater, 2004, 52(11): 3313-3332.
[3] ZHENG X J, ZHOU Y C, LI J Y. Nano-indentation fracture test of Pb(Zr0.52Ti0.48)O3 ferroelectric thin films [J]. Acta Mater, 2003, 51: 3985-3997.
[4] EMELYANOV A Y U, PERTSEV N A, KHOLKIN A L. Effect of external stress on ferroelectricity in epitaxial thin films [J]. Physical Review B, 2002, 66: 214108-1-214108-3.
[5] PERTSEV N A, ZEMBILGOTOV A G., TAGANTSEV A K. Effect of mechanical boundary conditions on phase diagrams of epitaxal ferroelectric thin films [J]. Physical Review Letters, 1998, 80(9): 988-1991.
[6] KOUKHAR V G, PERTSEV N A, WASER R. In-plane polarization states and their instabilities in polydomain epitaxial ferroelectric thin films [J]. Applied Physics Letters, 2001, 78: 530-532.
[7] LI Y L, HU T, LIU Z K, CHEN L Q. Phase-field model of domain structures in ferroelectric thin films [J]. Applied Physics Letters, 2001, 78: 3878-3880
[8] G.BAN Z, ALAY S P. Phase diagrams and dielectric response of epitaxial barium strontium titanate films: A theoretical analysis [J]. Journal of Applied Physics, 2002, 91(11): 9288-9296.
[9] CANEDY C L, LI H, ALPAY S P, RIBA L S, ROYTBURD A L, RAMESH R. Dielectric properties in heteroepitaxial Ba0.6Sr0.4TiO3 thin films: Effect of internal stresses and dislocation-type defects [J]. Applied Physics Letters, 2000, 77: 1695-1697.
[10] ALPAY S P, MISIRLIOGLU B, SHAMA A, BAN Z G. Structural characteristics of ferroelectric phase transformations in single- domain epitaxial films [J]. Journal of Applied Physics, 2004, 95(12): 8118-8123.
[11] CHANG W, GILMORE C M, KIM W J, POND J M, KIRCHOEFER S W, QADRI S B, CHRISEY D B, HORWITZ J S. Influence of strain on microwave dielectric properties of (Ba,Sr)TiO3 thin films [J]. Journal of Applied Letters, 2000, 87: 3044-3049.
[12] HYUM S, CHAR K. Effects of strain on the dielectric properties of tunable dielectric SrTiO3 thin films [J]. Applied Physics Letters, 2001, 79: 254-256.
[13] WANG J, ZHANG T Y. Effect of nonequally biaxial misfit strains on the phase diagram and dielectric properties of epitaxial ferroelectric thin films [J]. Applied Physics Letters, 2005, 86: 192905-1-192905- 3.
[14] ZEMBILGOTOV A G, PERTSEV N A, BOTTGER U, WASER R. Effect of anisotropy in-plane strains on phase states and dielectric properties of epitaxial ferroelectric thin films [J]. Applied Physics Letters, 2005, 86: 052903-1-052903-3.
[15] LIN Y, CHEN X, LIU S W, CHEN C L, JANG S L, LI Y, JIA Q X, BHALLA A. Anisotropy in-plane strains and dielectric properties in (Pb, Sr)TiO3 thin films on NdGaO3 substrates [J]. Applied Physics Letters, 2004, 84(4): 577-579.
[16] LEFKI K, DOMANS G J M. Measurement of piezoelectric coefficients of ferroelectric thin films [J]. Journal of Applied Physics, 1994, 76: 1764-1767.
[17] ALGUERO M, BUSHBBY A J, REECE M J, POYATO R, RICOTE J, CALZADA M L, PARDO L. Stress-induced depolarization of (Pb, La)TiO3 ferroelectric thin films by nanoindentation [J]. Applied Physics Letters, 2001, 79: 3830-3832.
[18] ABPLANALP M, FOUSEK J, GUNTER P. Higher order ferroic switching induced by scanning force microscopy [J]. Physical Review Letters, 2001, 86: 5799-5802.
[19] HAUN M J, FUMAN E, JANG S J, MCKINSTRY H A, CROSS L E. Thermodynamic theory of PbTiO3 [J]. Journal of Applied Physics, 1987, 62: 3331-3338.
[20] HAUN M J, FUMAN E, JANG S J, CROSS L E. Thermodynamic theory of the lead zirconate-titanate solid solution system: Part I-V [J]. Ferroelectrics, 1989, 99(13): 13-86.
[21] WU X M, LU X M, CHEN A P, YIN Y, MA J, LI W, KAN Y, QIAN D, ZHU J S. Stress effects on ferroelectric and fatigue properties of Nd- and La-doped Bi4Ti3O12 thin films [J]. Applied Pysics Letters, 2005, 86: 092904-1-092904-3.
(Edited by YUAN Sai-qian)
Foundation item: Project(10472099) supported the National Natural Science Foundation of China; Project(05JJ30208) supported by the Natural Science Foundation of Hunan Province; Project(05FJ2005) supported by Key Project of Scientific and Technological Department of Hunan Province; Project(GY2006-2) supported by Scientific and Technological Project of Xiangtan City
Corresponding author: DENG Shui-feng; Tel: +86-732-8293648; Fax: +86-732-8292468; E-mail: sfDeng@xtu.edu.cn