In this case, the measurement vector y is just a linear combination of the K columns of Θ, whose projection is ai>>0. Therefore, if we know a priori in which K entries of a are bigger than zero, then we can form an M×K system of linear equations to solve these non-zero entries. In this way, the number of equations M now equals or exceeds the number of unknowns K. To ensure that the M×K system is well-conditioned, the following equation must be satisfied for any vector v sharing the same K non-zero entries:
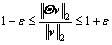 (5)
(5)
where ε>0 and || ||2 denotes the 2-norm in Eq. (5). The locations of the K non-zero entries in a cannot be determined in practice. Interestingly, a stable inverse for both K-sparse and compressible signals can be obtained when Θ satisfies Eq. (5) for an arbitrary 3K-sparse vector v. This condition is called restricted isometry property (RIP) [10-11]. Incoherence, a related condition, requires that the rows {Φi} of Φ must not sparsely represent the columns {Ψi} of Ψ.
The Gaussian matrix Φ is incoherent with the unit diagonal matrix I. Ψ is computed with the use of Eq. (2). According to RIP, the reconstructed effect becomes perfect for the Gaussian matrix when the measurement times M≥cK×lg(N/K), with c being a small constant [11]. This study estimates the sparsity of underwater acoustic signals, and the number of measurements is calculated as follows:
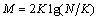 (6)
(6)
where Φ, y, and Θ can be calculated according to the M value.
The Gaussian matrix, Bernoulli matrix [12], Fourier matrix and Hadamard matrix [13] are always used as measurement matrixes in compressed sensing theory. Different measurement matrixes require various measurement times to accurately reconstruct the original signal.
2.2 Underwater acoustic signal reconstruction algorithm
The proposed IOMP algorithm chooses several columns that have the maximum correlation coefficient between the recovery matrix and the residual value and then advances these columns to the front of the recovery matrix. The recovery matrix is then rearranged by analogy. In this way, the proposed algorithm can reduce the computing time. The IOMP algorithm chooses the absolute value of the 2-norm difference between the original and the reconstructed signals as the stop condition of the loop iteration. The loop iteration will stop when the difference is less than the threshold value ε. Therefore, the IOMP algorithm is robust and can reconstruct the original signal whose sparsity is unknown. The inputs of the IOMP algorithm during the reconstruction include the recovery matrix Θ, the measurement values y, and the estimated sparsity K, whereas the output is the reconstructed signal x.
The correlation coefficient is calculated as follows:
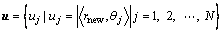 (7)
(7)
where θj is the jth column of Θ; rnew is the new residual value obtained by the iteration; uj is the correlation coefficient between θj and rnew. The IOMP algorithm uses Eqs. (8) and (9) to approach the original signal in the frequency domain and to update the residual value, respectively.
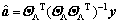 (8)
(8)
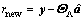 (9)
(9)
where 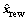 is the recovery signal in each iteration;
is the recovery signal in each iteration;  is the original signal in the frequency domain after each iteration; ΘΛ is the recovery matrix after the rearrangement in each iteration.
is the original signal in the frequency domain after each iteration; ΘΛ is the recovery matrix after the rearrangement in each iteration.
The principle and implementation of the IOMP algorithm are outlined as follows:
1) The IOMP algorithm sets the initial residual value as r0=y, sets the number of choosing columns in each iteration as L=3, and sets the index value as  f, J=f.
f, J=f.
2) The algorithm calculates the correlation coefficient u by using Eq. (7) and advances those columns that have the maximum correlation coefficient to the front of the recovery matrix.
3) The algorithm uses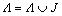 to update the support set
to update the support set  Λ.
Λ.
4) The algorithm calculates 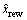 by using Eq. (8) and updates the residual value by using Eq. (9).
by using Eq. (8) and updates the residual value by using Eq. (9).
5) The algorithm will stop the iteration when the absolute value of the 2-norm difference between the original and the reconstructed signals is less than ε. Otherwise, the algorithm repeats all procedures from step 2.
6) After the iteration is stopped, the original signal is reconstructed by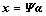 .
.
Figure 1 shows the implementation procedures of the underwater acoustic data compression method based on compressed sensing.
The principle and implementation of this compression method are outlined as follows:
1) A threshold is set to estimate the sparsity K of the original signal.
2) M=2Klg(N/K) is taken as the measurement times.
3) M is used to generate the measurement matrix Φ. Φ is then utilized to measure the original signal and to obtain the measurement values with the use of Eq. (4).
Most of the underwater acoustic signals are sparse in the frequency domain. In this study, Ψ is calculated with Eq. (2), and the recovery matrix Θ is calculated by Θ=ΦΨ.
5) The IOMP algorithm is used to calculate unknown variables with the use of the least square method [14-16] a=ΘT(ΘΘT)-1y.
6) The original signal is reconstructed by x=Ψa.
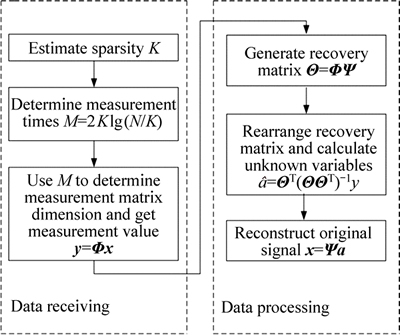
Fig. 1 Process flow diagram of underwater acoustic compression method
2.3 Compression algorithm evaluation indexes
The proposed compression method does not code for the underwater acoustic signal, so the method cannot be evaluated by the bits error ratio (BER). This study uses yCR, the cross correlation coefficient (R), the largest normalized frequency domain error (E), and the frequency domain quantization signal noise ratio y(FQSNR) as objective evaluation indexes. A favorable reconstructed effect is obtained when a large R, a small E, and a large yFQSNR are derived.
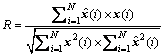 (10)
(10)
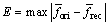 (11)
(11)
 (12)
(12)
where x(i) is the original signal; 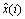 is the reconstructed signal;
is the reconstructed signal; 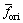 is the normalized frequency of the original signal;
is the normalized frequency of the original signal; 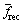 is the normalized frequency of the reconstructed signal; X(f) is the frequency domain description of the original signal; and e(f) is the difference between the original and the reconstructed signals in the frequency domain.
is the normalized frequency of the reconstructed signal; X(f) is the frequency domain description of the original signal; and e(f) is the difference between the original and the reconstructed signals in the frequency domain.
3 Single hydrophone signal compression
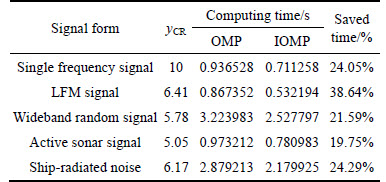
This study chooses the single frequency signal, the LFM signal, and the wideband random signal as the simulation signals and uses actual underwater acoustic signals to verify the compression method.
3.1 Analog signal simulation
The single frequency signal in this study is set as follows:
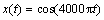 (13)
(13)
The sample frequency for all analog signals is set to 25 kHz. The waveform of LFM is expressed as follows:
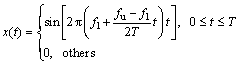 (14)
(14)
where fu and fl are the upper and lower frequency boundaries of the LFM signal, respectively; and T is the signal duration. In the simulation, fl is 7 kHz, fu is 8 kHz, and T is 1 s. The wideband random signal is generated by filtering of Gaussian white noise. The upper and lower frequency boundaries of the wideband random signal are 5.6 kHz and 7.4 kHz, respectively.
Figures 2(a) and (b) show the time domain, frequency domain, and power spectrum comparison diagrams of the original and reconstructed wideband random signals with different yCR. Figure 2(a) shows that the reconstructed signal retains the characteristics of the original signal in the time domain, frequency domain, and power spectrum. Therefore, this signal retains the effective components in the frequency domain when the yCR is 5.78. However, as shown in Fig. 2(b), a poor reconstructed effect is obtained when the yCR is 15.4.
Table 1 shows the compression evaluation results of the signals. The cross correlation coefficient between the original and the reconstructed signals of three typical underwater acoustic signals is above 0.99, the E is below 0.1, and the yFQSNR becomes large after 5 to 10 times data compression. Table 1 also shows that the single frequency signal obtains an acceptable reconstructed effect when the yCR is 24, the LFM signal obtains a poor reconstructed effect when the yCR is 13.33, and the wideband random signal obtains a poor reconstructed effect when the yCR is 15.4.
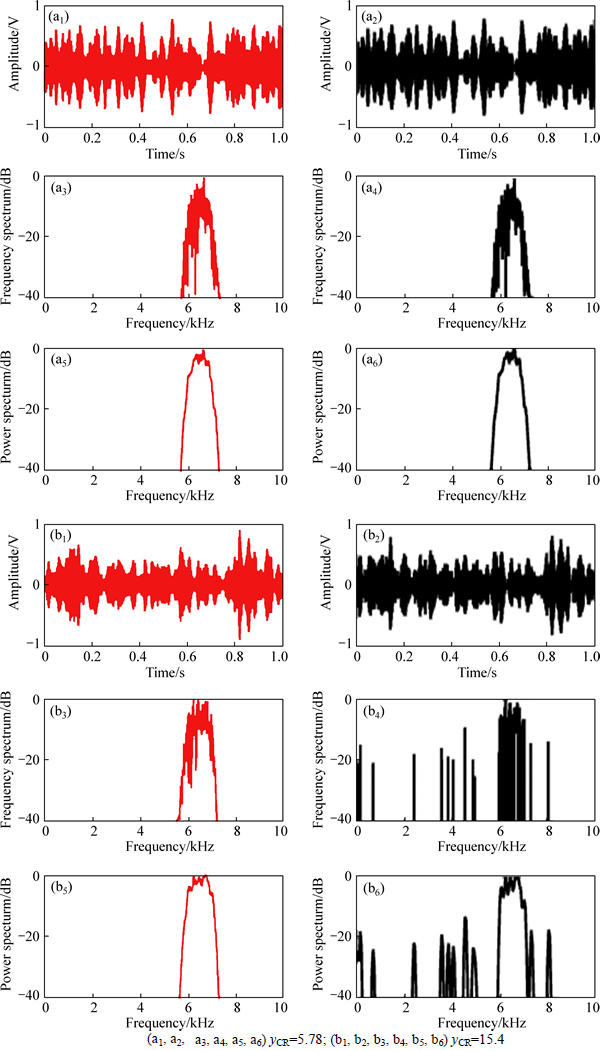
Fig. 2 Comparison diagrams of original (a1, a3, a5, b1, b3, b5) and reconstructed (a2, a4, a6, b2, b4, b6) wideband random signals:
Table 1 Compression results of simulation signals
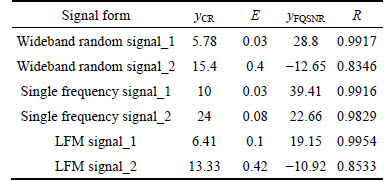
Unlike the LFM and wideband random signals, the single frequency signal is known to have few efficient points in the frequency domain. Therefore, the proposed compression method can obtain a high compression ratio for the single frequency signal, but it obtains a low compression ratio for the LFM and wideband random signals.
3.2 Actual underwater acoustic signal verification
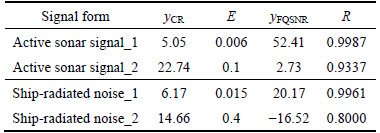
This study chooses two types of actual underwater acoustic signals, namely, active sonar signal and ship-radiated noise, to verify the compression method. The comparison diagrams of the original and the reconstructed signals are shown in Fig. 3. The active sonar signal and ship-radiated noise are accurately reconstructed when the yCR values are 5.05 and 6.17, respectively. Table 2 shows the compression evaluation results of the two signals with different yCR.
Table 2 shows that the cross correlation coefficient remains high, and the largest normalized frequency domain error remains low for actual underwater acoustic signals when the yCR is about 6. However, an unacceptable reconstructed effect is obtained when the yCR exceeds 10.
Table 2 Compression results of actual signals
3.3 IOMP algorithm advantages
The computing time of the OMP and IOMP algorithms are shown in Table 3. Only the loop iterative time is shown in Table 3. The IOMP algorithm reduces the computing time by about 20% after achieving a 5 to 10 times larger compression ratio.
4 Array signal compression
The above-mentioned signals are all single hydrophone signals, so an estimation experiment on a 12-element circle array DOA is performed in an anechoic tank to verify the validity of the proposed method for array signals. A transducer transmits a continuous wave (CW) pulse signal and a wideband random signal, and a uniform, 12-element circular array is used to receive the signal. The frequency of CW is 2.0 kHz, the sample frequency is 104 kHz, and the pulse width is 20 ms. The bandwidth of the wideband signal ranges from 500 Hz to 2.0 kHz. The transducer and the array have a depth of 3 m and a range of 10 m, whereas the 12-element array has a radius of 0.5 m. The sound speed is assumed to be at 1500 m/s.
Table 3 Computing time of OMP and IOMP algorithms
4.1 Narrowband signal experimental results
The circular array has a scanning range from 0° to 360°. Figure 4 shows the maximum receiving signal of each element. The amplitudes of elements No. 0 to No. 6 are bigger than those of elements No. 7 to No. 11. Therefore, elements No. 0 to No. 6 are considered the forward direction elements. Element No. 3 is chosen as the center element, and element No. 0 is scanned clockwise from the initial direction.
After the experimental data are obtained, this study uses the conventional beamformer (CBF) method and the minimum variance distortionless response (MVDR) method for DOA estimation. Figure 5 shows the DOA estimation diagrams of the narrowband signal with different yCR. The sidelobe level of the beam pattern increases with the increase of yCR. A DOA estimation error is obtained for both CBF and MVDR methods when the yCR is greater than 10. The DOA estimation error increases with the yCR, as shown in Fig. 6(a). To consider the effect of the signal noise ratio (SNR), white Gaussian noise is added to the experimental data.Figure 6(b) shows the DOA estimation error with a different SNR when the yCR is 10. When the SNR is too low, the reconstructed signal obtains a DOA estimation error. By contrast, no DOA estimation error is observed when the SNR exceeds 35 dB.
4.2 Wideband random signal experimental results
The wideband random signal is decomposed into narrowband components, which are then processed with the compression method. The final result is calculated by averaging of all narrowband components. Figures 7(a) and (b) show the results of the wideband random signal DOA estimation obtained by the CBF and MVDR methods. The proposed compression method is effective for the wideband random signal when the yCR is about 5. A DOA estimation error is obtained when the yCR is greater than 8.

Fig. 3 Comparison diagrams of original (a1, a3, a5, b1, b3, b5) and reconstructed (a2, a4, a6, b2, b4, b6) signals:
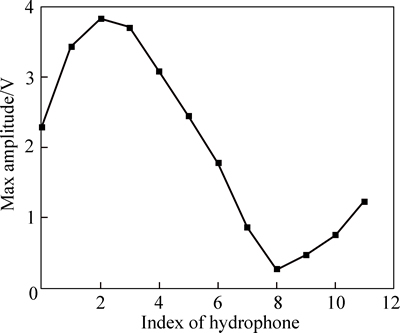
Fig. 4 Maximum receiving signal of a 12-element array
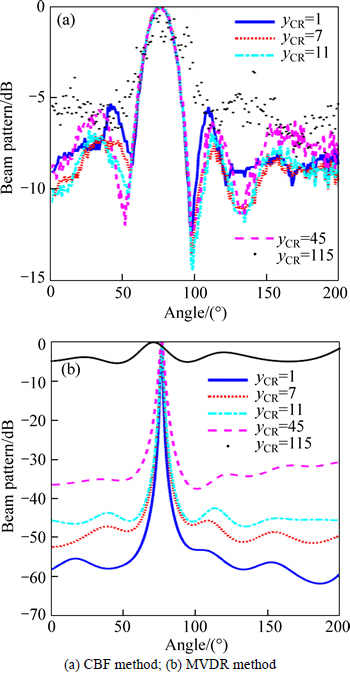
Fig. 5 DOA estimation diagrams of narrowband signal with different yCR:
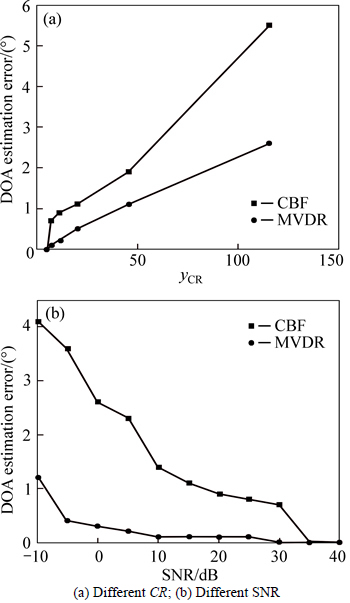
Fig. 6 DOA estimation error diagram with different yCR and SNR:
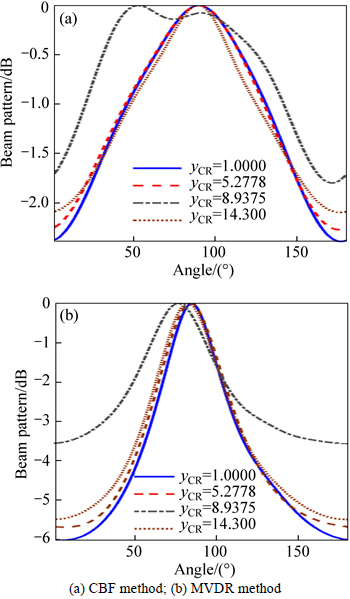
Fig. 7 DOA estimation diagrams of wideband signal with different yCR:
5 Conclusions
This study introduces an underwater acoustic data compression method based on compressed sensing. The underwater acoustic data are transformed into the sparse domain for data storage at the receiving terminal, and the IOMP algorithm is used to reconstruct the original underwater acoustic data at the data processing terminal. After the compression method is used, a single frequency or narrowband signal can obtain a high CR, whereas a wideband random signal obtains a low CR. When the correlation coefficient of the reconstructed and original signals is over 0.95, increasing the sidelobe level will seldom cause a DOA estimation error. The proposed method can increase the compression ratios for single frequency and wideband random signals by more than 10 and 5 times, respectively. The method can also alleviate the pressure of the underwater acoustic data transmission, reduce system costs, and significantly improve system efficiency. The IOMP algorithm can decrease the computing time by about 20% compared with the original OMP algorithm.
The simulation analyses that are performed in this study do not consider the effect of environment noise. A DOA estimation error is observed when the SNR is very low.
References
[1] SAYOOD K. Introduction to data compression [M]. United States: Newnes Press, 2006.
[2] JAIN A K. A fast Karhunen-Loeve transform for a random processes [M]. Chicago: IEEE Computer Society, 1974, 24: 1023-1029.
[3] TURCZA P, DUPLAGA M. Low-Power image compression for wireless capsule endoscopy [C]// IEEE International Workshop on Imaging Systems and Techniques-IST. Krakow, Poland, 2007: 1-4.
[4] MO Y B, QIU Y B, LIU J Z, LING Y X. A data compression algorithm baseed on adaptive huffman code for wireless sensor networks [C]// Intelligent Computation Technology and Automation (ICICTA). 2011: 3-6.
[5] SHEN Yan-chun, GUAN Yu-jun, WANG Fang, LUN Zhi-xin. The investigation of image compress coding based on wavelet transformation [C]// International Conference on Future Information Technology and Management Engineering. 2010: 324-326.
[6] BERGER C R, ZHOU S L, PREISIG J C. Sparse channel estimation for multicarrier underwater acoustic communication: From subspace methods to compressed sensing [J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1708-1721.
[7] DONOHO D L. Compressed sensing [J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[8] TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit [J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666.
[9] BOASHASH B, O'SHEA P. A methodology for detection and classification of some underwater acoustic signals using time- frequency analysis techniques [J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1990, 38(11): 1829-1841.
[10] CANDES E J, TAO T. Near-optimal signal recovery from random projections: universal encoding strategies [J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425.
[11] DAVENPORT M A, WAKIN M B. Analysis of orthogonal matching pursuit using the restricted isometry property [J]. IEEE Transactions on Information Theory, 2010, 56(9): 4395-4401.
[12] ZHANG Ge-sen, JIAO Shu-hong, XU Xiao-li, WANG Lan. Compressed sensing and reconstruction with bernoulli matrices [C]// IEEE International Conference on Information and Automation. 2010: 455-460. (in Chinese)
[13] GAN Lu, LI Ke-zhi, LING Cong. Golay meets hadamard: Golay- paired hadamard matrices for fast compressed sensing [C]// IEEE Information Theory Workshop. 2012: 637-641.
[14] TANG Gui-lin, QIU Yun-ming. Improved least square method apply in ship performance analysis [C]// International Conference on Advanced Computer Theory and Engineering (ICACTE). 2010: 594- 596.
[15] MARQUARDT D W. An algorithm for last-squares estimation of nonlinear parameters [J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431-441.
[16] LI Ling-zhi, ZOU Bei-ji, ZHU Cheng-zhang. Improved nonconvex optimization model for low-rank matrix recovery [J]. Journal of Central South University, 2015, 22(3): 984-991.
(Edited by YANG Hua)
Foundation item:Project(11174235) supported by the National Natural Science Foundation of China; Project(3102014JC02010301) supported by the Fundamental Research Funds for the Central Universities, China
Received date: 2015-06-11; Accepted date: 2015-11-19
Corresponding author: YANG Kun-de, Professor, PhD; Tel: +86-29-88460586; E-mail: ykdzym@nwpu.edu.cn