DOI: 10.11817/j.issn.1672-7207.2019.02.023
圆钢管UHPC短柱轴压承载力与变形能力计算模型
王震1,王景全1, 2,刘桐旭1,修洪亮1
(1. 东南大学 混凝土及预应力混凝土结构教育部重点实验室,江苏 南京,210096;
2. 东南大学 国家预应力工程技术研究中心,江苏 南京,210096)
摘要:根据力的平衡和变形协调,推导出钢管折减系数和核心混凝土增强系数的解析表达式,研究圆钢管约束对超高性能混凝土(UHPC)轴压强度的增强作用和环向应力对圆钢管轴压强度的折减作用;建立圆钢管UHPC短柱轴压承载力计算模型,并与已有的规范方法进行比较;基于Mander模型,根据横向约束等效原则,建立圆钢管约束UHPC单轴受压本构模型,并利用理想弹塑性模型建立能够考虑环向应力影响的圆钢管单轴受压本构模型,实现对圆钢管UHPC短柱轴压受力全过程的模拟,并与试验结果进行比较。研究结果表明:与规范方法相比,承载力模型能够更好地兼顾计算精度和可靠度;利用变形能力计算模型得到的全过程荷载-位移曲线与试验结果较吻合。
关键词:钢管混凝土;超高性能混凝土;轴压承载力;变形能力;变形协调
中图分类号:TU398.6 文献标志码:A 文章编号:1672-7207(2019)02-0428-09
An analytic model for axial load capacity and deformation capacity of short columns of circular UHPC filled steel tube
WANG Zhen1, WANG Jingquan1, 2, LIU Tongxu1, XIU Hongliang1
(1. Key Laboratory of Concrete and Prestressed Concrete Structure of China Ministry of Education,Southeast University, Nanjing 210096, China;
2. National Prestress Engineering Research Center, Southeast University, Nanjing 210096, China)
Abstract: Due to force equilibrium and deformation compatibility, the expressions of steel tube reduction coefficient and core concrete strengthen coefficient were deduced to study the improvement of confinement of steel tube on axial strength of ultra high performance concrete (UHPC) and the reduction of circumferential stress on axial strength of steel tube. Based on the above two factors, an analytic model for load capacity of circular UHPC filled steel tube stub columns was established, and the proposed model was compared with several conventional standard methods. According to the equivalence principle of transverse confinement, the axial compressive constitutive model was established for circular steel tube confined UHPC based on Mander model. Ideal elastic-plastic model was modified to take the effect of circumferential stress into account for the axial compressive constitutive model of circular steel tube. The two above models were used to simulate the axial compressive load-deformation curve of short columns with circular UHPC filled steel tube. The results show that compared with several methods given by standards, the axial load capacity model shows good calculation precision and reliability, the axial compressive load-deformation curve given by the proposed model is in good agreement with that of trial results.
Key words: concrete filled steel tube; ultra high performance concrete; axial load capacity; deformation capacity; deformation compatibility
超高性能混凝土(ultra high performance concrete, UHPC)因具有较高的抗压强度和弹模、可利用的抗拉强度、良好的变形能力以及耐腐蚀等优点,自问世以来便引起了人们的重视[1]。一方面,国内外研究者针对UHPC的制备和基本性能开展了大量研究[2-5];另一方面,UHPC也已从实验室研究走向工程应用[6]。迄今为止,世界上已经有100多座桥梁使用UHPC,日本的羽田机场则利用UHPC制作了20多万m2的飞机跑道和停机坪[7]。此外,UHPC与圆钢管组合而成的圆钢管UHPC柱也开始应用于高层建筑中[7-8]。作为承压构件,圆钢管UHPC短柱的轴压性能至关重要。吴炎海等[9-10]进行了圆钢管UHPC短柱的轴压试验,给出了轴压承载力回归公式以及圆钢管UHPC整体的单轴受压应力和应变关系;田志敏等[11]通过试验研究了圆钢管UHPC短柱在轴压作用下的受力变形机理与破坏特点;GULER等[12]通过试验研究了钢管强度和径厚比对承载力和延性的影响,并对各国规范中的方法进行了评价;罗华等[13]通过试验研究了加载方式的影响。综上可知:当前针对圆钢管UHPC短柱轴压承载力和变形能力的研究多基于试验,缺少相关的理论计算模型。现有的关于圆钢管混凝土短柱轴压承载力的计算方法主要分为2类:一类是将钢管混凝土视为统一体,研究其组合性能[14-15];另一类是将钢管和核心混凝土分开研究。其中,第2类又分为2种:一种是不考虑两者的相互作用,如美国ACI规范[16];另一种是考虑两者的相互作用,即考虑钢管约束对核心混凝土抗压强度的增强作用和钢管环向应力对钢管轴向承载力的削弱作用[17-20]。然而,已有研究表明[21],相比于普通混凝土,UHPC具有较小的泊松比,侧限压力对UHPC抗压强度的提高程度也更小[21],因此,现有计算方法不能直接应用于圆钢管UHPC短柱。此外,钢管和核心混凝土的相互作用是由于核心混凝土横向膨胀受到钢管约束而产生的,两者之间应满足变形协调[22],现有的计算方法对此也未有充分考虑。本文作者在现有的考虑钢管和核心混凝土相互作用计算方法的基础上,引入变形协调条件,并计入UHPC材料特性的影响;建立圆钢管UHPC短柱轴压承载力计算模型,并利用已有试验结果对建议模型和美国ACI规范[16]、欧洲EC4规范[20]以及我国CECS28:2012[23]中的方法进行评价;同时,利用已有的关于箍筋约束UHPC的研究成果,按照横向约束等效原则,建立基于Mander模型的圆钢管约束UHPC单轴受压本构模型,结合考虑了钢管环向应力折减作用的钢材理想弹塑性模型,实现对圆钢管UHPC短柱轴压受力全过程荷载位移曲线的模拟,并将计算结果与试验结果进行比较。
1 圆钢管UHPC短柱轴压承载力计算模型
现有的考虑钢管和核心混凝土相互作用的圆钢管混凝土短柱轴压承载力Nu的计算[17-20]公式如下:
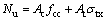 (1)
(1)
式中:Ac为核心混凝土面积;fcc为圆钢管约束UHPC的峰值应力;At为圆钢管面积;σtx为考虑环向应力折减后圆钢管轴压强度。
记φc=fcc/fc(其中φc为核心混凝土轴压强度增强系数,fc为UHPC圆柱体抗压强度),φt=σtx/fy(其中φt为钢管轴压强度折减系数,fy为圆钢管屈服强度),则有
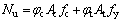 (2)
(2)
建议模型通过引入变形协调来考虑UHPC材性的影响,推导出关于圆钢管UHPC短柱承载力计算所需的φc和φt这2个系数的解析公式。
1.1 基本假设
1) 圆钢管UHPC短柱仅发生强度破坏,且破坏前钢管和UHPC黏结良好,两者之间无相对滑移。
2) 圆钢管UHPC短柱仅承受轴压荷载,柱子被均匀压缩,并符合平截面假定,暂未计入偏心影响。
3) 核心UHPC各向同性,在达到极限受压应力之前近似按弹性状态分析。钢管应力应变关系屈服前满足线弹性,屈服后满足米塞斯屈服(MISE)准则。
1.2 模型建立与公式推导
圆钢管和核心UHPC的受力示意图如图1所示,其中t为钢管壁厚;D为钢管直径;p为钢管与核心混凝土之间的径向压强;T为沿轴向单位高度钢管环向合力;dc为核心混凝土直径;σtx为钢管轴向应力;σtθ为钢管环向应力;σtr为钢管径向应力;N为钢管轴向压力。核心UHPC三向受压,圆钢管微元体可近似视为二向应力状态。
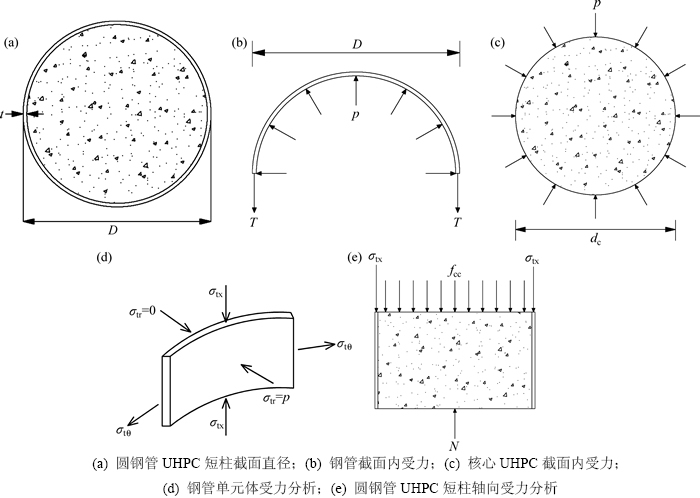
图1 钢管和核心UHPC受力示意图
Fig. 1 Force diagrams between steel tube and core UHPC
柱坐标系下核心UHPC的物理方程式如下:
 (3)
(3)
式中:Ec和μc分别为核心UHPC的弹性模量和泊松比;σx,σθ和σr分别为核心UHPC轴向应力、环向应力和径向应力;εx,εθ和εr分别为核心UHPC轴向应变、环向应变和径向应变。
圆钢管UHPC短柱在轴压状态下,可近似认为核心UHPC环向与径向应力相等,即
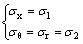 (4)
(4)
式中:σ1和σ2分别为核心UHPC轴向和横向(水平向)主应力。
将式(4)代入式(3)可以得到
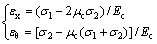 (5)
(5)
式(5)中以压应力及应变为正值,拉应力及应变为负值,因此,εx>0,εθ<0,即核心UHPC轴向应变εx为压应变,环向应变εθ为拉应变。为计算方便,在求解过程中保持εθ为正值,即
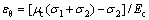 (6)
(6)
由图1(d)可以得到钢管轴向和环向应变表达式 如下:
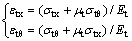 (7)
(7)
式中:εtx和εtθ分别为钢管轴向和环向应变;Et和μt分别为钢管的弹性模量和泊松比。
由变形协调可知:钢管轴向应变εtx等于核心UHPC轴向应变εx,钢管环向应变εtθ等于核心UHPC环向应变εθ,即
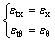 (8)
(8)
将式(5)~(7)代入式(8),可以得到
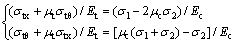 (9)
(9)
沿轴向单位高度钢管环向应力σtθ产生的合力T与核心UHPC在轴压荷载下产生的横向外扩力P相平衡(见图1),即
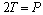 (10)
(10)
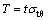 (11)
(11)
 (12)
(12)
将式(11)和式(12)代入式(10),得到钢管环向应力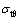 为
为
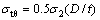 (13)
(13)
已知双向侧限混凝土轴向应力σ1与圆柱体抗压强度fc和侧限应力σ2的关系式[18]如下:
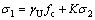 (14)
(14)
式中:K为侧限系数,对于普通混凝土,取值范围为4.1~5.6[24]。已有研究表明,随着侧向压力增大,UHPC抗压强度增加幅度比普通混凝土的小[21],故本文将UHPC的侧限系数K取为4.1;γU为混凝土强度直径折减系数,其计算公式如下:
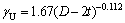 (15)
(15)
将式(13)~(14)代入式(9),则 可表示为
可表示为
 (16)
(16)
其中:
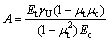 (17)
(17)
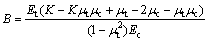 (18)
(18)
将式(13)~(14)和式(16)代入式(9),并定义χ2为核心混凝土侧限压力系数( ),则有
),则有
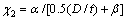 (19)
(19)
其中:
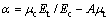 (20)
(20)
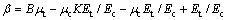 (21)
(21)
定义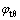 为圆钢管环向应力系数(
为圆钢管环向应力系数(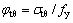 ),由式(13)可知:
),由式(13)可知:
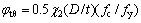 (22)
(22)
由式(16)可知钢管轴压强度折减系数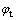 为
为
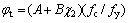 (23)
(23)
由式(23)计算得到φt>1,这对于屈服后满足MISE准则的钢管显然是不合适的,因此,需要对式(23)进行修正。由钢管应力满足MISE准则可以得到
 (24)
(24)
将式(24)整理后得到满足MISE准则的钢管轴压强度折减系数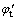 为
为
 (25)
(25)
由式(14)可知核心混凝土轴压强度增强系数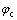 为
为
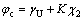 (26)
(26)
2 轴压承载力计算模型试验验证及其与各国规范方法的比较
2.1 各国规范方法
欧洲的EC4规范[20]给出了圆钢管混凝土柱轴压承载力计算公式(见式(2)),其中钢管混凝土柱截面有效刚度Seff计算公式为
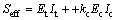 (27)
(27)
式中:It为钢管的惯性矩;Ic为核心混凝土的惯性矩;kc为考虑混凝土开裂的刚度折减系数,取0.6。
圆钢管混凝土柱稳定承载力计算公式为
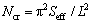 (28)
(28)
式中:L为柱的计算长度。
圆钢管混凝土柱的塑性承载力特征值Npl,Rk为
 (29)
(29)
圆钢管混凝土柱的相对长细比λ为
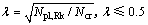 (30)
(30)
EC4规范中钢管轴压强度折减系数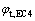 为
为
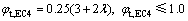 (31)
(31)
EC4规范中核心混凝土轴压强度增强系数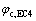 为
为
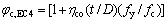 (32)
(32)
其中:
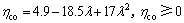 (33)
(33)
美国ACI规范[16]给出的圆钢管混凝土短柱轴压承载力计算公式则简单得多,没有考虑核心混凝土与钢管的相互作用。
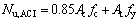 (34)
(34)
我国的CECS28:2012“钢管混凝土结构设计与施工规程”[23]中规定的圆钢管混凝土短柱轴压承载力计算公式为
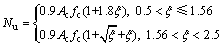 (35)
(35)
其中:ξ=Atfy/(Acfc)。
2.2 试验验证
利用本文建议模型与各国规范方法对收集到的51根圆钢管UHPC短柱试件的轴压承载力进行计算,试件的具体参数见表1(其中,Nexp为轴压承载力度验值),承载力计算值与试验值对比分别见图2和表2。
从图2可以看出:本文建议模型与EC4方法的承载力计算值与试验值较吻合;ACI方法因为乘以折减系数0.85,计算结果较试验结果偏小;CECS28:2012方法中承载力计算值比试验值大,安全性较低。
表1 试件参数
Table 1 Parameters of specimens

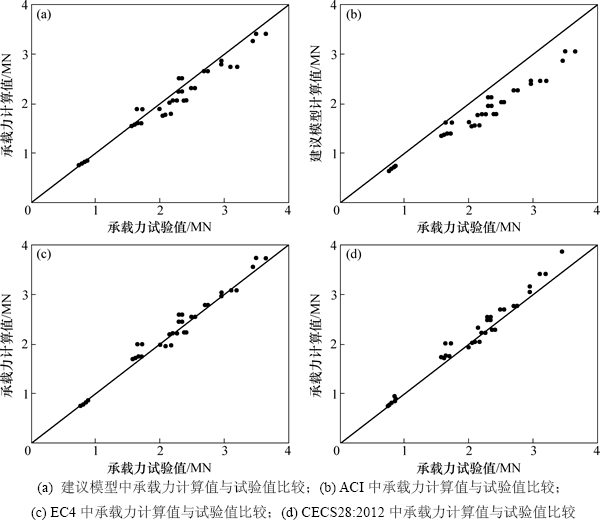
图2 不同方法试件承载力计算值与试验值比较
Fig. 2 Comparison of calculated and experimental loading capacity using different methods
表2 不同方法试件轴压承载力比较
Table 2 Comparison of loading capacities of specimens different methods
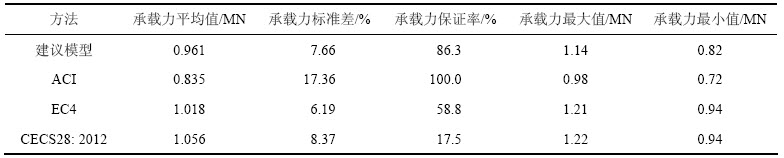
不同方法试件承载力比较见表2。从表2可以看出:与建议模型相比,EC4方法试件承载力平均值最接近试验值,且对应的标准差也更小,但承载力保证率(即承载力试验值小于承载力计算值的试件个数占总个数的比例)只有58.8%,远小于建议模型的86.3%。因此,综合考虑精度和可靠度,建议模型更适合在设计中使用。
3 圆钢管UHPC短柱轴压变形能力计算模型
为评价圆钢管UHPC短柱的轴压变形能力,需要计算得到圆钢管UHPC短柱轴压受力全过程荷载-位移曲线。为此,本文分别采用基于Mander模型的圆钢管约束UHPC单轴受压本构模型和能够考虑环向应力影响的钢管单轴受压本构模型,并将试验结果与由上述2种材料模型计算得到的荷载-位移曲线进行对比,验证本文方法的正确性。
3.1 基于Mander模型的圆钢管约束UHPC单轴受压本构模型
Mander模型能够较好地考虑各种约束形式对混凝土的约束效果[24],在抗震设计中得到了较广泛的应用,其表达式如下:
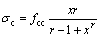 (36)
(36)
式中:x和r为计算参数,x=εc/εcc,r=Ec/(Ec-Esec);割线模量Esec=fcc/εcc。
因此,利用Mander模型确定圆钢管约束UHPC单轴受压应力应变关系,需要的参数包括无约束UHPC的弹性模量Ec,以及约束UHPC的峰值应力fcc和对应的应变εcc。
GRAYBEAL根据试验研究结果,建议无约束UHPC的弹性模量计算公式[2]为
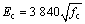 (37)
(37)
关于圆钢管约束UHPC的峰值应力fcc和对应的应变εcc的计算方法尚未见报道。
SUGANO等[25]通过试验给出了箍筋约束UHPC峰值应力时对应的应变的计算公式为
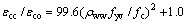 (38)
(38)
式中:ρww为面积配箍率;fyv为箍筋屈服强度;εco为无约束UHPC的峰值应力对应的应变,其计算公式[25]为
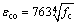 (39)
(39)
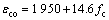 (40)
(40)
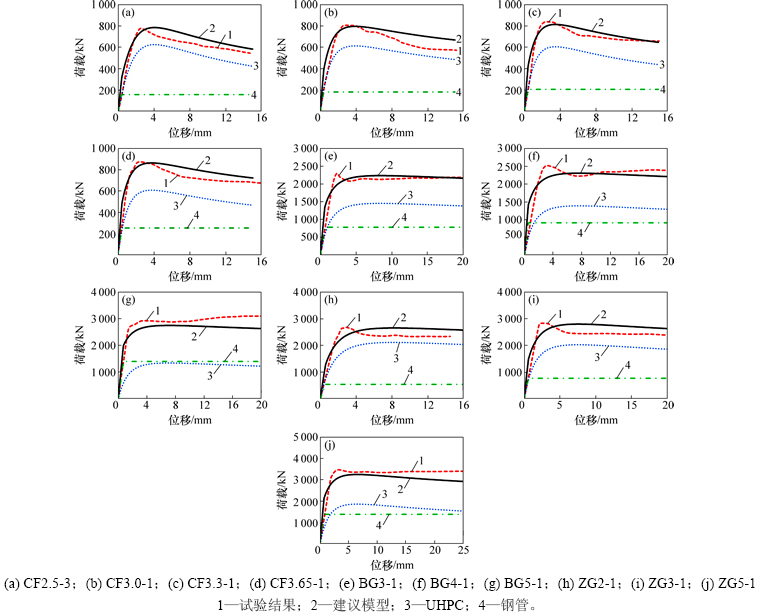
图3 不同试件荷载-位移曲线比较
Fig. 3 Comparisons of loading-displacement curves for different specimens
本文取式(37)和式(38)计算所得εco的平均值作为计算结果,即
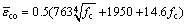 (41)
(41)
本文采用横向约束等效原则,给出圆钢管约束UHPC峰值应力时对应的应变计算公式为
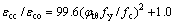 (42)
(42)
圆钢管约束UHPC的峰值应力fcc计算公式如下:
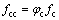 (43)
(43)
3.2 考虑环向应力影响的圆钢管单轴受压本构模型
为考虑环向应力的影响,对理想弹塑性模型进行修正,将修正后的理想弹塑性模型作为圆钢管单轴受压本构模型。考虑环向应力影响的修正后圆钢管单轴受压应力fs为
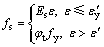 (44)
(44)
式中: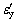 为修正后的屈服应变,
为修正后的屈服应变,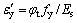 。
。
3.3 轴压变形能力计算模型试验验证
选择10根试件,验证圆钢管UHPC短柱轴压变形能力计算模型的准确性。不同试件荷载-位移曲线如图3所示。由图3可以看出:建议模型中各试件荷载-位移曲线与试验中试件荷载-位移曲线较吻合。
4 结论
1) 与EC4,ACI和CECS28: 2012规范方法相比,本文提出的圆钢管UHPC短柱轴压承载力计算模型兼顾了计算精度和可靠度,可用于工程设计。
2) 利用基于Mander模型的圆钢管约束UHPC单轴受压本构模型和考虑环向应力影响的圆钢管单轴受压本构模型可以得到圆钢管UHPC短柱轴压全过程荷载-位移曲线,且其与试验结果较吻合。
参考文献:
[1] GRAYBEAL B A. Material property characterization of ultra-high performance concrete[R]. Washington D C, USA: Federal Highway Administration, 2006: 1.
[2] GRAYBEAL B A. Compressive behavior of ultra-high-performance fiber-reinforced concrete[J]. ACI Materials Journal, 2007, 104(2): 146-152.
[3] GRAYBEAL B A, BABY F. Development of direct tension test method for ultra-high-performance fiber-reinforced concrete[J]. ACI Materials Journal, 2013, 110(2): 177-186.
[4] 张哲, 邵旭东, 李文光, 等. 超高性能混凝土轴拉性能试验[J]. 中国公路学报, 2015, 28(8): 50-58.
ZHANG Zhe, SHAO Xudong, LI Wenguang, et al. Axial tensile behavior test of ultra high performance concrete[J]. China Journal of Highway and Transport, 2015, 28(8): 50-58.
[5] 徐世烺, 蔡向荣, 张英华. 超高韧性水泥基复合材料单轴受压应力-应变全曲线试验测定与分析[J]. 土木工程学报, 2009, 42(11): 79-85.
XU Shilang, CAI Xiangrong, ZHANG Yinghua. Experimental measurement and analysis of the axial compressive stress-strain curve of ultra high toughness cementitious composites[J]. China Civil Engineering Journal, 2009, 42(11): 79-85.
[6] 徐世烺, 李贺东. 超高韧性水泥基复合材料研究进展及其工程应用[J]. 土木工程学报, 2008, 41(6): 45-60.
XU Shilang, LI Hedong. A review on the development of research and application of ultra high toughness cementitious composites[J]. China Civil Engineering Journal, 2008, 41(6): 45-60.
[7] 郑文忠, 吕雪源. 活性粉末混凝土研究进展[J]. 建筑结构学报, 2015, 36(10): 44-58.
ZHEN Wenzhong, LU Xueyuan. Literature review of reactive powder concrete[J]. Journal of Building Structures, 2015, 36(10): 44-58.
[8] 金何伟, 刘中宪, 刘申永, 等. 钢管超高强钢纤维混凝土柱抗爆性能试验研究[J]. 建筑结构, 2016, 46(4): 45-49.
JIN Hewei, LIU Zhongxian, LIU Shenyong, et al. Experimental study of ultra-high performance fiber reinforced concrete filled steel tube columns under blast loading[J]. Building Structures, 2016, 46(4): 45-49.
[9] 吴炎海, 林震宇. 钢管活性粉末混凝土轴压短柱受力性能试验研究[J]. 中国公路学报, 2005, 18(1): 57-62.
WU Yanhai, LIN Zhenyu. Experimental study of behavior on RPC filled steel tubular stub columns under axial compression[J]. China Journal of Highway and Transport, 2005, 18(1): 57-62.
[10] 林震宇, 吴炎海, 沈祖炎. 圆钢管活性粉末混凝土轴压力学性能研究[J]. 建筑结构学报, 2005, 26(4): 52-57.
LIN Zhenyu, WU Yanhai, SHEN Zuyan. Research on behavior of RPC filled circular steel tube columns subjected to axial compression[J]. Journal of Building Structures, 2005, 26(4): 52-57.
[11] 田志敏, 张想柏, 冯建文, 等. 钢管超高性能 RPC 短柱的轴压特性研究[J]. 地震工程与工程振动, 2008, 28(1): 99-107.
TIAN Zhimin, ZHANG Xiangbo, FENG Jianwen, et al. Characteristics of RPC-filled steel tubular puncheons with ultra high performance subjected to axial compressive loading[J]. Journal of Earthquake Engineering and Engineering Vibration, 2008, 28(1): 99-107.
[12] GULER S,  OPUR A, AYDOGAN M. Axial capacity and ductility of circular UHPC-filled steel tube columns[J]. Magazine of Concrete Research, 2013, 65(15): 898-905.
OPUR A, AYDOGAN M. Axial capacity and ductility of circular UHPC-filled steel tube columns[J]. Magazine of Concrete Research, 2013, 65(15): 898-905.
[13] 罗华, 季文玉, 闫志刚, 等. 加载方式对钢管活性粉末混凝土短柱抗压性能影响的研究[J]. 铁道学报, 2014, 36(9): 105-110.
LUO Hua, JI Wenyu, YAN Zhigang, et al. Research on influence of loading methods on compressive behavior of reactive powder concrete filled steel tube stub columns under axial loads[J]. Journal of the China Railway Society, 2014, 36(9): 105-110.
[14] 钟善桐. 钢管混凝土结构[M]. 北京: 清华大学出版社, 2003: 141-143.
ZHONG Shantong. The concrete-filled steel tubular structures[M]. Beijing: Tsinghua University Press, 2003: 141-143.
[15] 韩林海, 杨有福. 现代钢管混凝土结构技术[M]. 中国建筑工业出版社, 2007: 83-85.
HAN Linhai, YANG Youfu. Technology of modern steel tube concrete structure[M]. China Building Industry Press, 2007: 83-85.
[16] ACI 318-05, Building code requirements for structural concrete and commentary[S].
[17] 蔡绍怀. 现代钢管混凝土结构[M]. 人民交通出版社, 2003: 45-54.
CAI Shaohuai. Modern steel tube confined concrete structures[M]. China Communications Press, 2003: 45-54.
[18] SAKINO K, NAKAHARA H, MORINO S, et al. Behavior of centrally loaded concrete-filled steel-tube short columns[J]. Journal of Structural Engineering, 2004, 130(2): 180-188.
[19] 周绪红, 刘界鹏, 张素梅. 圆钢管约束钢筋混凝土短柱的轴压力学性能[J]. 工程力学, 2009, 26(11): 53-59.
ZHOU Xuhong, LIU Jiepeng, ZHANG Sumei. Behavior of circular tubed reinforced concrete stub columns under axial compression[J]. Engineering Mechanics, 2009, 26(11): 53-59.
[20] BS EN 1994-1-1: 2004, Eurocode 4: design of composite steel and concrete structures—part 1-1, general rules and rules for buildings[S].
[21] FEHLING E, SCHMIDT M, WALRAVEN J, et al. Ultra-high performance concrete UHPC: fundamentals, design, examples[M]. Berlin, Germany: John Wiley & Sons, 2014: 44.
[22] CHOI K K, XIAO Y. Analytical studies of concrete-filled circular steel tubes under axial compression[J]. Journal of Structural Engineering, 2009, 136(5): 565-573.
[23] CECS28:2012, 钢管混凝土结构设计与施工规程[S].
CECS28:2012, Technical specification for concrete-filled steel tubular structures[S].
[24] MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804-1826.
[25] SUGANO S, KIMURA H, SHIRAI K. Study of new RC structures using ultra-high-strength fiber-reinforced concrete (UFC)-The challenge of applying 200 MPa UFC to earthquake resistant building structures[J]. Journal of Advanced Concrete Technology, 2007, 5(2): 133-147.
(编辑 伍锦花)
收稿日期:2018-04-01;修回日期:2018-06-06
基金项目(Foundation item):国家自然科学基金资助项目(51438003);国家科技支撑计划项目(2011BAJ09B02);江苏高校优势学科建设工程资助项目(CE02-1-4)(Project(51438003) supported by the National Natural Science Foundation of China; Project(2011BAJ09B02) supported by National Key Technology Research and Development Program of China; Project(CE02-1-4) supported by the Priority Academic Program Development of Jiangsu Higher Education Institutions)
通信作者:王景全,博士,教授,从事组合结构桥梁和桥梁抗震等研究;E-mail:wangjingquan@seu.edu.cn