基于PBM+MPC的球磨机动态优化控制

马天雨，桂卫华，阳春华，王雅琳

(中南大学 信息科学与工程学院，湖南 长沙，410083)

摘要：提出一种基于分批试验结论和考虑工况的球磨机连续磨矿粒级质量平衡模型(PBM)改进模型。基于某些粒级不符合一级磨矿动力学的分批试验结果改进破碎率模型；为消除干扰影响，建立破碎率模型参数和各工况变量间的LSSVM关系模型；基于改进模型，采用PBM+MPC实现球磨机优化控制。仿真结果表明，PBM+MPC能有效消除过程干扰，稳定过程产品质量。

关键词：LSSVM；PBM；球磨机；预测控制

中图分类号：TP273          文献标志码：A         文章编号：1672-7207(2012)02-0528-06

Ball-mill dynamic optimization control based on PBM+MPC

MA Tian-yu, GUI Wei-hua, YANG Chun-hua, WANG Ya-ling

(School of Information Science and Engineering, Central South University, Changsha 410083, China)

Abstract: An improved ball mill PBM model considering the conditions for continuous operation was proposed based on the batch-grinding results. The breakage-rate model was improved according to the batch-grinding results that some certain size does not meet first-order grinding kinetic. To eliminate the influence of disturbances, a LSSVM relationship model between the parameters of breakage rate model and the manipulated variables was built. To realize the optimization control of ball mill, a PBM+MPC scheme was proposed based on the new model. Simulation results show that PBM+MPC can eliminate the disturbances and stabilize the product quality of the process efficiently.

Key words: LSSVM; PBM; ball-mill; predictive control

磨矿分级过程是将粗矿粒磨细并将粗细矿粒分离的选矿过程，为浮选作业提供浓细度合适的矿浆。目前，国内大部分磨矿分级过程仍然依据专家经验手动调节，因此，难以保证过程的优化运行。磨矿分级过程，存在弱非线性和大滞后等特性，是典型的复杂工业过程。在早期研究中，基于操作量和被控量关系的传函矩阵^[1-3]是磨矿回路主要模型形式。为消除矿石硬度变化对系统影响，建立矿石硬度软测量模型^[1]和多模型切换机制，铁鸣等^[10-11]对磨矿过程建模及优化控制等进行了研究，但这些模型都没有考虑原矿下料粒径变化、钢球磨损和助磨药剂等工况对模型的影响。磨矿过程早期控制方案是多回路PID解耦控制^[4]，而该方案存在明显缺点：输入、输出难以匹配；PID是基于反馈的控制方法，而磨矿过程存在较大滞后，导致该方案无法实现过程实时控制。目前，模型预测控制(MPC)已经成为化工过程应用最广的多变量控制算法^[1-3]，将MPC应用于有如下特性的系统时优势明显：可多输入、多输出，操作变量和被控变量有约束，系统存在延时和弱非线性。在此，本文作者针对由球磨机和螺旋分级机组成的磨矿过程，建立基于分批试验结论的改进PBM模型。考虑矿石硬度、钢球磨损和原矿粒径变化等干扰影响，建立了下料量、入磨水流量、磨机电流和加药剂量等操纵变量和模型参数间的LSSVM模型。为消除干扰、稳定二级溢流细度，采用PBM+MPC实现球磨机动态优化控制。

1  磨矿过程

磨矿的目的是得到粒度适宜、基本单体解离的矿粒，及时排出合格的细粒产物，将粗矿粒返回再磨。磨矿产品质量(排矿细度)影响浮选效率和尾矿中有用金属含量，因此，将排矿细度稳定控制在工艺范围对提高选矿过程效率至关重要。

磨矿过程如图1所示：破碎车间首先将大块矿石破碎成细矿料(粒度小于19 mm)，细矿料均化后经料斗中的震动筛均匀撒在传送带上，称为原矿下料。原矿料经传送带送球磨机入口处的进料器。由于采用湿磨方式，因此，需要给球磨机注入一定量的水。为了提高研磨效率，磨机中添加了一定量的碳酸钠溶液，作为碱性助磨药剂。原矿料、入磨水和助磨剂在进料器混合后形成磨机入料，进入球磨机。球磨机是1个被电机带动绕轴旋转的柱形钢筒，内装有大量钢球作为研磨介质，转动的球磨机带动钢球将混合矿浆中的粗矿料研磨、破碎成细矿料，细矿料以矿浆形式溢出球磨机排矿口，混合排矿水后进入高堰式螺旋分级机(一级分级机)。堰分由沉降槽和1个旋转的螺旋板组成，螺旋板在旋转过程中将沉降槽底部粗料推进返砂槽形成一级返砂，由入磨水冲入进料器，与新加物料一起进入磨机重磨；较细矿料以矿浆形式溢出沉降槽，形成一级溢流，混合一级溢流水后进入原矿槽，被水泵送入沉没式螺旋分级机(二级分级机)。溢流细度受磨矿细度和排矿水、一级溢流水影响，而排矿细度是决定因素，因此，本文只研究球磨机排矿细度的优化控制问题。

2  球磨机建模

2.1  PB模型

被磨矿料由粒径不等的各种颗粒组成。为了简单起见，试验中连续磨矿过程和分批试验分别采用11个和7个不同孔径的筛子，即13.20，9.50，5.60，3.35，2.00，0.85，0.50，0.25，0.15，0.075，0.045 mm和2.00，0.85，0.50，0.25，0.15，0.075，0.045 mm。其中，17 mm是最大孔径，0.045 mm是最小孔径。因此，实验中分别筛分出12和8个不同粒级矿料。

PBM以物料平衡原理为基础，即磨机内某粒级物料变化量等于较大颗粒破碎后生成该粒级的质量分数减去该粒级被破碎的质量分数，即：

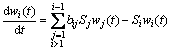       (1)

式中：w_i(t)表示第i个粒级在t时刻的质量分数；b_ij为破碎分布函数，其物理意义是第j粒级的物料经过1次破碎后进入第i粒级的质量分数；S_j为选择函数，也叫破碎率函数，反映了磨矿的速率。

解方程(1)可以得到 PBM 递推解即里德解^[5]。由于里德解将磨机入料作为模型参数计算，对于同一磨机，入料粒级分布不同时需要重新计算模型参数。因此，Austin等^[6-8]在里德解基础上推出了转换函数解：

          (2)

       (3)

       (4)

其中：d_ij和c_ij为递推参数；d_ij为1个下三角矩阵，它就是球磨机单元模型；p_i为磨机排矿中第i粒级物料所占的质量分数；f_j为磨机入料中第j粒级物料所占的质量分数。式(2)表明：p_i是d_ij和f_j的线性组合，其中0＜d_ij＜1。由式(2)~(4)可以看出模型的未知参数是e_j，S_i和b_ij。

e_j可由下式计算：

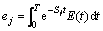             (5)

式中：E(t)为停留时间分布密度函数，由示踪法测试得到，具体推导过程见文献[7]；T为物料在磨机中的最长停留时间；S_j是第j粒级代表破碎率。b_ij是1个下三角矩阵，分批试验测得破碎分布函数如表1所示，表中：b_j1代表由第1粒级矿粒破体产生其他粒级矿体产生其他粒级矿粒的质量分数；“0”表示矿石破碎后不能产生等于或大于自身粒级的矿粒。研究表明：破碎分布函数b_ij只与矿石性质有关，而与工况基本无关^[8]，且破碎分布函数b_ij反映矿石的研磨特性^{[6, 9]}， 0＜b_ij＜1。

图1  磨矿过程

Fig.1  Grinding process

表1  破碎分布函数b_ij

Table 1  Breakage distribution function

2.2  改进破碎率模型

PBM有2条假设^[5]：(1) 各粒级矿粒的破碎率不受其被研磨时间和在磨机中停留位置的影响，各粒级矿粒破碎率都符合一阶磨矿动力学；(2) 模型精度不受工况影响。

分批磨矿实验某矿石破碎率如表2所示。由表2可以看出：除粒级0.45~0.75，0.23~0.42和0.50~0.23 μm外，其他各粒级都不符合一阶动力学特性(破碎率随时间变化)。因此，改进原破碎率模型^[5]为：

           (6)

给原模型加入e^-βt项，β可按表1中不同粒径矿粒在不同研磨时间破碎率变化情况经计算得到。仿真结果表明：该改进模型可以描述破碎率随时间变化的非一阶特性。

表2  各粒级破碎率分批试验结果

Table 2  Batch test results for breakage rate of various size

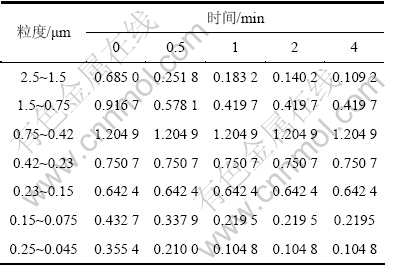
对于连续磨机，因为无法检测具体粒级的研磨时间，因此，无法将破碎率改进模型式(6)直接带进球磨机模型。但在连续磨机模型中，矿石破碎分布函数b_ij由矿石性质决定，与工矿无关，并由分批试验数据根据分批磨矿球磨机模型反算得到；b_ij对连续磨矿模型精度影响很大。因此，将式(6)代入分批球磨机模型，可以反算出更加符合被磨矿石性质b_ij，从而可以提高连续磨机预测精度。

2.3  LSSVM关系模型

为克服干扰，消除工况对模型精度的影响，需要建立各工况与磨机排矿细度的关系模型。经研究分析，选择4个工况变量，分别是：原矿下料量R_ore，入磨水流量R_win，磨机电流C和助磨药剂量R_cosNa3。PBM中影响排矿细度的主要因素是入料各粒级质量分数和各粒级破碎率，因此，为了稳定磨机排矿细度，建立各操纵量和破碎率模型参数间的LSSVM^[12-13]关系模型，如图2所示。

图2  LSSVM关系模型

Fig.2  LSSVM relationship model

采样数据经BILMAT软件协调、剔除后，取剩余45组数据作为现场数据，由fmincon( )非线性约束优化函数单组优化45组a，α，μ和Λ，然后调用trainlssvm( )函数训练每组数据对应的工况与a，α，μ和Λ间的LSSVM模型。随意选择40训练数据，剩余6组作为预测数据，调整核函数参数直到预测结果符合要求，最后得到LSSVM关系模型。预测时，首先将预测结果对应工况输入LSSVM模型，得到a，α，μ和Λ，与τ，e_j，s_j和b_ij一起代入PB模型得到磨机排矿各粒级质量分数，经简单计算便可得到排矿细度(即粒度低于0.075 mm的矿粒所占的质量分数)。

3  球磨机优化控制

将二级溢流液细度稳定控制在工艺指标范围是磨矿分级过程控制的主要目标，而影响溢流细度的根本因素是磨机排矿细度。本文重点研究球磨机排矿细度的稳定控制问题。通过研究磨矿过程，根据过程特点选择基于改进PBM的MPC实现其优化控制。

3.1  预测模型

上面建立了工况和破碎率模型参数间的LSSVM关系模型，所选工况是磨机排矿细度的4个主要影响因素，也是现场经常调节的操纵变量。因此，以R_m，R_win，R_out和R_cosNa3作为操纵变量，以磨机排矿细度为预测输出的改进PBM可以作为MPC的MISO预测模型。当受到较大干扰时，MPC控制器操纵变量最优值，R_m，R_win，R_out和R_cosNa3经调节后送入LSSVM模型，得到破碎率模型参数，代入PBM最终可计算磨机排矿细度。在下一个控制周期中，MPC根据排矿细度反馈误差及测量工况重新计算最优操纵变量，这样就实现了球磨机排矿细度稳定控制。

3.2  模型预测控制(MPC)

MPC基本原理可描述为：在每一个采样周期，给定过程预测模型和被控量设定值，在操作量和被控量约束范围内，计算使得系统输出最接近设定值的最优操作量。

预测控制问题在数学上就是根据操作量和控制量约束范围，求解误差二次性能目标函数最小值。用式(4)所示的模型表示MIMO动态系统：

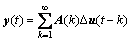
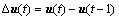            (7)

其中：y(t)为输出向量，表示3个被控对象C_fc，F_fc和C；u(t)为输入向量，表示4个操作变量(R_m，R_win，R_out和R_cosNa3)；A(k)为系统阶跃响应系数动态矩阵。根据式(7)，可得到第i步反馈校正输出：

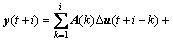
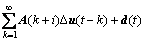
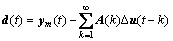        (8)

d(t)是由干扰、模型失配和测量误差等因素引起的预测误差；Δu(t+i-k)就是待优化最优控制输入序列。MPC算法公式化为：

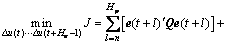
         (9)

其中：n为最小预测时域；H_p代表最大预测时域；H_u为控制时域，且一般有H_u≤u≤H_p-1；e(t+l)和y_r(t+l)分别代表预测误差和输出设定值；ρ为输出误差和输入调节量在目标函数中的权重，ρ越大，表明控制器反应越快，但是稳定性降低；Q和R是目标函数误差对角权矩阵和输入对角权矩阵，反映不同操纵量、控制量在目标函数中所占的比例。若要将某一系统输出量严格控制在设定点，则将其对应的权值调大，若输出可在某一范围内偏离设定值，则可将其对应的权值调小。同样，对于系统输入，若某一操作量的调节费用较高，则将其对应的权值调大，而将调节费用相对较低的操作量对应的权值调小。

调用QP算法可解上述命题，算法取如下约束：

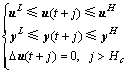           (10)

4  仿真结果分析

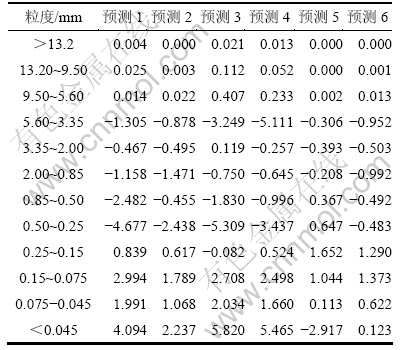
现场采样的50组数据通过BILMAT软件进行协调后，去除不合理数据点，从剩余46数据(磨机入料、排矿各粒级质量分数及对应工况)中随机选择40组作为拟合数据，6组作为预测数据。经粒子群算法优化，LSSVM核函数参数γ和σ分别选为63和0.1。预测时，将6组预测数据对应工况作为LSSVM模型输入，可直接得到破碎率模型参数，与τ，e_j，s_j和b_ij一起代入PB模型便可得到以磨机入料各粒级(12个粒级)质量分数为输入量，排矿各粒级(12个粒级)质量分数作为预测输出，受各操纵变量影响的球磨机改进PB模型。表3所示为模型预测结果，将6组预测数据入料各粒级质量分数和对应工况输入PB模型后，得到磨机排矿各粒级所占质量分数，然后，由实测质量分数减去预测质量分数得到模型预测粒度分布的绝对误差，每组数据预测输出12个不同粒级。由表3可知：该模型具有较高的预测精度，可以作为球磨机连续磨矿预测模型。

表3  模型预测结果

Table 3  Model predicted results  %

矿石硬度和下料粒径变化是系统的输入干扰，在simulink中用白噪声驱动的积分环节代替系统测量干扰；钢球添加、过磨引起的模型失配可通过修改模型参数调节。预测时域H_p、控制时域分别H_u分别取5和2，并取Q=0.1，ρ=0.3。被控量设定细度取75%。MPC控制器中，各操作量约束如下：

85＜R_m＜95 t/h；

75＜R_win＜95 m³/h；

82＜R_out＜87 A；

10＜R_cosNa3＜30 m³/h            (11)

在模型匹配、失配情况下，MPC控制结果分别如图3和图4所示。图中细度w表示粒径低于75 μm的颗粒所占质量分数。细度突降尖峰点是由干扰引起。从图4可以看出：PBM+MPC在模型失配、匹配时都能很好地将排矿细度稳定控制在75%设定点，只是模型失配时系统启动超调较大。

图3  匹配模型控制结果

Fig.3  Control results with match model

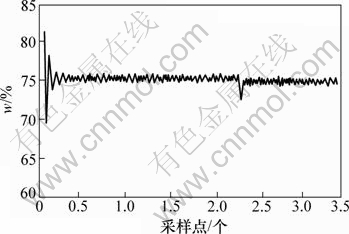
图4  失配模型控制结果

Fig.4  Control results with mismatch model

由于采用4×1的胖模型，控制器具有较大的控制余量，在稳定排矿细度的同时，为提高过程产量，减少钢球添加量和电量消耗，将式(11)进行如下改进：

95＜R_m＜95 t/h；

75＜R_win＜85 m³/h；

80＜R_out＜85 A；

15＜R_cosNa3＜25 m³/h            (12)

式(12)将下料量稳定在95 t/h(提高过程产量)，入磨水最大值改小至85 t/h(增加磨机内矿浆浓度，提高物料停留时间，增加细度)，磨机电流减小2 A(减少钢球添加量，从而减少磨机电耗)。因为pH变化范围小，因此，减小了药剂添加量范围。以式(9)为约束的MPC仍然能很好地将排矿细度稳定在75%。

对MPC控制器余量有一定限制，约束太紧会引起如图5所示结果。当较大干扰发生时，过程失控，导致被控量完全偏离设定点。

图5  约束范围太小时的控制结果

Fig.4  Control results with tight constraints

5  结论

(1) 为实现球磨机优化控制，使得球磨机稳定运行在最优点附近，对某矿石进行大量分批试验，发现某些粒级磨矿过程不符合一阶磨矿动力学，应改进PBM破碎率模型。

(2) 为消除由于下料硬度变化以及钢球磨损和水压不稳等不确定干扰因素的影响，建立下料量、入磨水流量、磨机电流和碳酸钠溶液添加量等操作参数和模型参数间的LSSVM模型，提高模型预测精度。

(3) 过程干扰导致溢流细度偏离生产指标，为稳定过程产品质量，采用基于改进PBM的MPC控制策略，实现球磨机优化控制。仿真结果证明了该方案的有效性，为磨矿过程优化控制提供了新思路。

参考文献：

[1] CHEN Xi-song. Application of model predictive control in ball mill grinding circuit[J]. Minerals Engineering, 2007, 20(11): 1099-1108.

[2] Radhakrishnan V R. Model based supervisory control of a ball mill grinding circuit[J]. Journal of Process Control, 1999, 9(3): 195-211.

[3] Ramasamy M. Control of ball mill grinding circuit using model predictive control scheme[J]. Journal of Process Control, 2005, 15(3): 273-283.

[4] Pomerleau A, Hodouin D, Desbiens A, et al. A survey of grinding circuit control methods: From decentralized PID controllers to multivariable predictive controllers[J]. Powder Technol, 2000, 108(2/3): 103-115.

[5] 尹蒂, 李松仁. 选矿数学模型[M]. 长沙: 中南工业大学出版社, 1993.
YING Di, LI Song-ren. Mathematical models of mineral processing[M]. Changsha: Central South University of Technology Press, 1993: 118-188.

[6] Austin L G, Brame K. A comparison of the Bond method for sizing wet tumbling mills with a size-mass balance simulation model[J]. Powder Technology, 1983, 34(2): 261-274.

[7] Austin L G. An introduction to the mathematical description of grinding as a Rate process[J]. Powder Technology, 1971, 5(1): 1-17.

[8] Kelsall D F, Reid K J, Restarick C J. Continuous grinding in a small wet ball mill. Part II. A study of the influence of hold up weight[J]. Powder Technology, 1969, 2(3): 162-168.

[9] Klimpel R R. Applications of a model for the analysis of liberation from a binary system[J]. Powder Technology, 1984, 39(1): 117-128.

[10] 铁鸣, 岳恒. 磨矿分级过程的混合智能建模与仿真[J]. 东北大学学报, 2007, 28(5): 609-612.
TIE Ming, YUE Heng. Hybrid intelligent modeling and simulation for ore grinding and classification process[J]. Journal of Northeastern University, 2007, 28(5): 609-612.

[11] 李勇. 磨矿过程参数软测量与综合优化控制的研究[D]. 大连: 大连理工大学控制科学与工程学院, 2006: 85-93.
LI Yong. Research on the parameters’ soft sensing and synthetic optimization of grinding process[D]. Dalian: Dalian University of Technology. School Science and of Control Engineering, 2006: 85-93.

[12] 张学工. 统计学习的本质[M]. 北京: 清华大学出版社, 2000: 128-162.
ZHANG Xue-gong. The nature of statistical learning[M]. Beijing: Tsinghua University Press, 2000: 128-162.

[13] Suykens J A K, van Gestel T, et al. Least squares support vector machines[M]. Singapore: World Scientific, 2002: 20-28.

(编辑 陈灿华)

收稿日期：2011-02-11；修回日期：2011-04-05

基金项目：国家自然科学基金重点资助项目(60634020)；国家自然科学基金资助项目(60874069，60804037)

通信作者：马天雨(1978-)，男，甘肃白银人，博士，从事复杂工业过程建模与优化研究；电话：13755151369；E-mail：pymty@yahoo.com