地铁道岔轨顶坡对尖轨磨耗的影响

徐井芒，王平，曾晓辉，肖杰灵

(西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都，610031)

摘要：针对地铁道岔磨耗严重及使用寿命短等问题，利用有限元方法建立道岔区三维弹塑性轮轨接触计算模型，通过计算尖轨接触应力、接触斑面积及内部应力等，分析轨顶坡对尖轨磨耗的影响。模型中车轮型面采用实测磨耗状态LM型车轮型面。研究结果表明：设置轨顶坡时，尖轨接触应力及内部应力均比不设置轨顶坡的小；以尖轨顶宽35.5 mm断面为例，当轨顶坡从1/40增大到1/20时，其接触应力最大值从904.267 MPa减小至686.266 MPa，Von Mises应力最大值从552.123 MPa降低至493.755 MPa，状态由塑性变形转变为弹性变形，有利于减小尖轨磨耗；增大尖轨断面顶面宽度可以提高其受力状态，延长道岔使用寿命；综合考虑尖轨受力状态，1/20轨顶坡优于其他轨顶坡。

关键词：尖轨磨耗；有限元法；轨顶坡；接触应力；Von Mises应力；弹塑性

中图分类号：U213.2          文献标志码：A         文章编号：1672-7207(2014)08-2899-06

Effect of rail top slope on subway switch rail wear

XU Jingmang, WANG Ping, ZENG Xiaohui, XIAO Jieling

(Key Laboratory of High-speed Railway Engineering, Ministry of Education,

Southwest Jiaotong University, Chengdu 610031, China)

Abstract: In view of existing states of subway switch’s serious wear and short service life, a three-dimensional elastic-plastic model of wheel-rail contact in turnout zone was established by the finite element method to analyze the effect of rail top slope on switch rail wear by calculating contact stresses, contact plaque areas and internal stresses of switch rail. In the model, the measured wear profile of LM type was adopted for the wheel profile. The results show that when the rail top slope is set, the stresses and internal stresses of switch rail are small. Taking the section as an example whose top width size is 35.5 mm, when the rail top slope increases from 1/40 to 1/20, the maximum contact stress decreases from 904.267 MPa to 686.266 MPa, and the maximum Von Mises stress decreases from 552.123 MPa to 493.755 MPa, whose status converts from the plastic deformation stage to the elastic deformation stage, and this will cause the decrease of the wear. The increase of switch rail’s top width can improve the stress state and increase service life, and the rail top slope 1/20 is superior to others on comprehensive consideration of the switch rail’s stress state.

Key words: switch rail wear; finite element method; rail top slope; contact stress; Von Mises stress; elastic-plasticity

道岔是机车车辆实现转向的重要线路设备，是决定行车速度和安全的主要因素。道岔结构复杂，不仅体现于其轨线布置和走行线路转换，而且在于其多变的轮轨关系。合理的轮轨型面匹配对改善车辆运行平稳性和提高道岔通过能力，降低轮轨接触应力和磨耗，提高轮轨疲劳寿命与保证行车安全具有重要意义^[1]。轮轨几何条件是影响磨损和疲劳的重要因素之一，合理设置轮轨几何参数，可以在一定程度上减缓轮轨磨损和疲劳，其中轨底坡(对于道岔尖轨而言，通常设置轨顶坡)的设置对降低轮轨横向力和冲角、改善轮轨接触条件，从而减缓钢轨侧磨和疲劳是至关重要的^[2]。目前，国内外关于轮轨几何型面配合与轮轨接触关系的研究很多，但大多是从车轮型面角度改善轮轨接触匹配关系，以减少钢轨的疲劳和磨耗。金学松等^[3]利用非Hertz滚动接触理论分析计算了2种车轮踏面与钢轨之间滚动接触斑的弹性位移、应变和应力的分布情况，结果表明这2种车轮踏面与钢轨接触的力学行为有一定区别。Wu^[4]提出型面扩展法来设计车轮踏面，优化轮轨型面匹配。张剑等^[5]改进了扩展方法并用其对LMA踏面进行了局部改进，降低了轮轨接触应力。Santamaria等^[6]基于等效锥度曲线，采用基因遗传算法优化车轮踏面，降低了轮轨接触应力，提高了车辆的动力学性能。崔大宾等^[7-8]提出考虑轮轨法向间隙参数的车轮踏面优化方法，并对我国高速及重载列车车轮型面进行优化设计。赵伟等^[9]利用三维有限元轮轨接触模型研究了新旧车轮与新旧钢轨匹配接触问题，指出适应旧轨轨头的车轮踏面设计，有利于减缓轮轨磨耗；成棣等^[10]应用响应面方法进行车轮踏面的优化设计，优化后车轮踏面较原车轮踏面的磨耗指数降低52%左右。事实上，在轮轨滚动接触过程中，轨道的几何结构参数对接触行为的影响也相当大。如李霞等^[11]利用Kalker三维非赫兹接触理论及其改进算值方法研究了轨底坡对2种踏面形式接触行为的影响，结果表明不同车轮型面与轨底坡的匹配性能明显不同。王文健等^[12]利用三维弹性体非赫兹滚动接触理论及其数值程序CONTACT研究轨底坡、轨距和曲线半径等轨道参数对轮轨滚动接触应力的影响，提出优化轨道参数的建议。为此，本文作者根据现场实测的地铁车辆LM型磨耗车轮型面和地铁道岔的实际几何尺寸，建立道岔区轮轨接触三维弹塑性有限元模型，对不同轨顶坡的尖轨接触应力、接触斑面积及内部应力分布等进行计算，分析轨顶坡对尖轨磨耗的影响。

1  磨耗车轮测量与尖轨轨顶坡设置

1.1  磨耗车轮测量

为统计使用的车轮型面形状，利用丹麦Miniprof轮轨廓形测量仪测量324组地铁车辆车轮型面，见图1。对实测车轮型面处理除去噪声点后，通过3次样条曲线拟合获得车轮型面轮廓线。从图1可以看出：所测得车轮磨耗状态不同，型面差异性显著。对实测的车轮型面进行平均化处理，代表磨耗状态车轮型面，见图2。与标准车轮型面相比，磨耗状态的车轮型面变化较大，车轮踏面和轮缘根部均发生磨损，其中车轮踏面最大磨耗量为1.59 mm，车轮轮缘根部的磨耗量为1.34 mm。

图1  实测车轮型面

Fig. 1  Measured wheel profiles

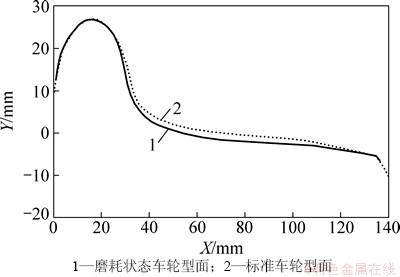
图2  车轮型面磨耗程度

Fig. 2  Wear degree of wheel profile

1.2  尖轨轨顶坡设置

从现场调研道岔伤损情况看，尖轨伤损主要发生在尖轨轨头轨距角部位，如图3和图4所示。当车轮轮缘与尖轨贴靠时，轮轨接触点位于尖轨轨距角圆弧附近，加之轨距角及轮缘根部圆弧半径较小，导致接触应力过大，使尖轨发生磨损及疲劳掉块等损伤^[13]，因此，可以进一步通过优化尖轨顶面轮廓，以降低接触应力。

图3  尖轨侧面磨耗

Fig. 3  Side wear of switch rail

图4  尖轨剥离掉块

Fig. 4  Shelling defects of switch rail

在确保尖轨各断面降低值(即基本轨与尖轨顶面高差)不变的前提下，仅改变尖轨轨顶坡来改变尖轨型面，尖轨轨顶坡分别取值为无轨顶坡以及1/20，1/30和1/40等，并选取尖轨顶宽20.0，35.5和50.0 mm等关键断面为例，计算接触应力。与区间线路相比，岔区尖轨轨顶坡的设置较复杂，且截面型式变化明显，不同轨顶坡下尖轨各关键断面的截面形式见图5。

图5  不同轨顶坡下各关键断面的截面形式

Fig. 5  Cross section types of key turnout section with different rail top slopes

2  轮轨接触模型的建立

2.1  计算理论

地铁列车侧向通过道岔时，在惯性力作用下轮缘会与尖轨贴靠，造成尖轨侧磨。由于在接触区存在很大接触应力，轨头和踏面已发生塑性变形。为考虑轮轨接触区的局部塑性变形，本文轮轨材料采用双线性随动强化弹塑性材料模型，服从Mises屈服准则和随动强化准则。

Mises屈服准则可用下式描述：

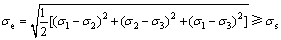 (1)

式中：σ_e为等效应力；σ₁，σ₂和σ₃为3个主应力；σ_s为屈服强度。当等效应力σ_e满足式(1)时材料发生屈服。

根据弹塑性理论，双线性强化塑性材料模型的应力应变方程为

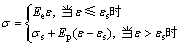         (2)

式中：E_e为弹性模量；E_p为应变弹性模量；σ_s为屈服强度；ε_s为屈服点总应变。

地铁道岔钢轨材质采用U71Mn，其材料参数为：E_e=214 GPa；E_p=14.898 GPa；σ_s=526 MPa^[14]。假设车轮材料和钢轨材料相同，其材料应力应变曲线见图6。

2.2  有限元模型

根据现场实测的车轮型面数据，以磨耗状态车轮型面与不同轨顶坡尖轨型面，采用有限元方法建立轮轨接触的三维有限元模型。轮轨材料等效应力-应变曲线见图6。由于轮轨接触区半径远小于接触表面的曲率半径，可知接触区应力远大于非接触区应力，即接触区存在明显应力集中，为此，轮对与道岔接触的部分网格划分较密，而远离接触的部分网格划分逐渐稀疏，这样既能满足接触计算精度的要求，又能节省计算时间。

当轮缘与尖轨贴靠时，轮对与道岔左右钢轨接触位置不对称，因此，建模时取整体轮对。轮轨接触整体有限元模型与局部有限元模型分别见图7和图8。模型计算参数如下：荷载包括轴重和横向力，轴质量取16 t，横向力取6.4×10⁴ N，其中轮对两侧车轮轮心上各施加一半的轴重力，横向力施加于轮轴端部轴中心线部位；地铁车辆轮对内侧距为1 353 mm，车轮半径为420 mm；轮轨间材料摩擦因数取0.30，泊松比取0.28。

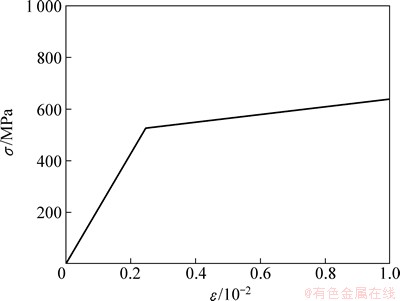
图6  轮轨材料等效应力-应变曲线

Fig. 6  Equivalent stress-strain curve of wheel/rail material

图7  整体有限元模型

Fig. 7  Whole finite element model

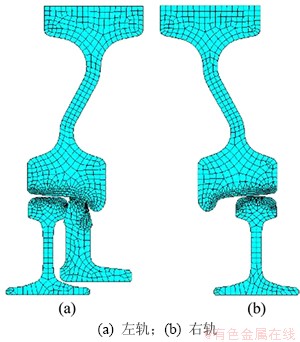
图8  局部有限元模型

Fig. 8  Part finite element model

3  计算结果分析

3.1  轧顶坡对接触应力的影响

在磨耗状态下，车轮与采用不同轨顶坡的尖轨接触时，尖轨接触应力及其接触斑面积随轨顶坡变化情况如图9和图10所示。

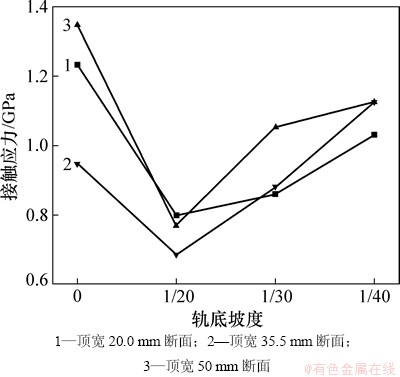
图9  接触应力与轨顶坡度的关系

Fig. 9  Relationship between contact stress and rail top slope

图10  接触斑面积与轨顶坡度的关系

Fig. 10  Relationship between contact plaque area and rail top slope

轨顶坡度对尖轨接触应力的影响较大。当不设置轨顶坡时，尖轨接触应力较设置轨顶坡时显著增加；以顶宽35.5 mm断面为例，当轨顶坡度从1/40增加到1/20时，尖轨接触应力从686.266 MPa增大至904.267MPa，增大幅度为24.11%；接触斑面积从244.740 mm²减小至195.045 mm²，减小幅度为25.47%。其他关键断面接触应力及接触斑面积随轨顶坡度的变化规律相同，当轨顶坡度设置为1/40时，其接触应力小于其他轨顶坡度时的应力。从图9和图10可以看出：随着轨顶坡度取值增大，尖轨接触应力显著减小，而接触斑面积则相应增大，几乎呈线性相关。

分析比较尖轨各关键断面接触应力及接触斑面积可以看出：尖轨顶宽20.0 mm和35.5mm断面接触应力较顶宽50.0 mm断面接触应力要小，而其接触斑面积比它要大。对于尖轨顶宽50.0 mm之前断面，轮载由基本轨和尖轨共同承受，使得尖轨承受的轮载相对较小，相应断面接触应力存在一定程度降低；随着尖轨断面顶面宽度增加，轮载由基本轨逐渐向尖轨转移；当尖轨断面足够粗壮时，轮载全部由尖轨承受，其接触应力有所增加，之后接触应力水平基本稳定。另外，由于尖轨顶宽20.0 mm断面较薄弱，承载宽度有限，导致其接触斑面积较顶宽35.5 mm断面面积要小，故其接触应力较大。

3.2  对内部应力的影响

不同轨顶坡时尖轨各关键断面Von Mises应力最大值见表1。以尖轨顶宽35.5 mm断面为例，不同轨顶坡度下尖轨断面Von Mises应力分布云图见图11。尖轨Von Mises应力最大值与轨顶坡度关系见表1。

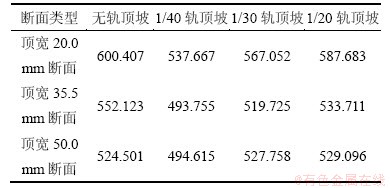
由表1可知：尖轨各关键断面内部应力随轨顶坡度变化规律相似，当轨顶坡度为1/40时，其Von Mises应力较小；随着尖轨顶面宽度的增大，其Von Mises应力最大值有所降低。这说明增加尖轨薄弱断面的粗壮度能够在一定程度上降低其内部应力水平，减缓塑性变形累计，提高尖轨使用寿命。

根据弹塑性理论计算结果，在静轮载作用下，尖轨顶宽20.0 mm断面Von Mises应力较大且已超过钢轨的屈服强度，表明已经进入塑性变形阶段，将导致该处尖轨的磨耗严重；其他2个关键断面Von Mises应力较小，这与现场道岔尖轨磨耗在顶宽20.0 mm断面最严重相一致。

表1  不同断面类型的尖轨Von Mises应力最大值

Table 1  Switch rail maximum Von Mises stresses of various section types            MPa

由图11可知：轨顶坡度对尖轨内部应力影响显著，随着轨顶坡度取值的增大，尖轨的最大Von Mises应力减小；从无轨顶坡增大到1/40时，尖轨断面Von Mises应力最大值从552.123 MPa降低至493.755 MPa，降低幅度为10.57%。由此可以看出：通过设置尖轨轨顶坡，能够使轮载在基本轨与尖轨之间进行重新分配，尖轨所承受轮载比例减小，有效地改善尖轨受力状态，降低伤损发生的可能性；此外，尖轨断面Von Mises应力最大值均发生距钢轨表面2.7~4.5 mm力最大值均发生距钢轨表面2.7~4.5 mm 范围内，表明该范围内容易产生塑性变形，且当塑性变形累计超过一定限值时，钢轨内部裂纹便开始萌生，最终导致道岔伤损发生。

图11  尖轨顶宽35.5 mm断面的Von Mises应力

Fig. 11  Von Mises stresses of 35.5 mm widen section of switch rail

4  结论

(1) 尖轨轨顶坡对其接触应力影响较大。不设置轨顶坡时，尖轨接触应力较设置轨顶坡时显著增加；设置轨顶坡时，尖轨接触应力随着轨顶坡的增大而减小。轨顶坡对尖轨接触斑面积影响规律恰恰相反。

(2) 尖轨轨顶坡对尖轨内部应力影响较大。不设置轨顶坡时，尖轨各关键断面Von Mises应力最大值均超过钢轨屈服强度，已进入塑性变形阶段，这将导致尖轨的磨耗严重。通过设置轨顶坡，尖轨Von Mises应力水平出现一定程度降低，有利于轮轨型面匹配，减缓尖轨磨耗。

(3) 随着尖轨顶宽的增大，尖轨的接触应力及内部应力均出现一定程度降低，可以通过增加尖轨顶面宽度(即增大尖轨断面粗壮度)延长道岔使用寿命。

(4) 综合考虑轨顶坡对尖轨各关键断面接触应力和内部应力的影响规律，尖轨1/20轨顶坡优于其他轨顶坡，有利于轮轨型面匹配，减缓尖轨磨耗及疲劳伤损的发生。

(5) 本文通过分析地铁道岔轨顶坡对轮轨接触应力及内部应力的影响，得出了更适合的岔区钢轨轨顶坡参数，可为地铁道岔的优化设计提供参考。

参考文献：

[1] 张军, 贾小平, 孙传喜, 等. 磨耗车轮与曲线钢轨接触关系[J]. 交通运输工程学报, 2011, 11(3): 29-33.

ZHANG Jun, JIA Xiaoping, SUN Chuanxi, et al. Contact relationship of wear wheel and curved rail[J]. Journal of Traffic and Transportation Engineering, 2011, 11(3): 29-33.

[2] 李霞, 温泽峰, 金学松, 等. 轨底坡对轮轨滚动接触行为的影响[J]. 机械强度, 2009, 31(3): 475-480.

LI Xia, WEN Zefeng, JIN Xuesong. Effect of rail cant on wheel/rail rolling contact behavior[J]. Journal of Mechanical Strength, 2009, 31(3): 475-480.

[3] 金学松, 温泽峰, 张卫华. 两种型面轮轨滚动接触应力分析[J]. 机械工程学报, 2004, 40(2): 5-11.

JIN Xuesong, WEN Zefeng, ZHANG Weihua. Analysis of contact stresses of wheel and rail with two types of profiles[J]. Chinese Journal of Mechanical Engineering, 2004, 40(2): 5-11.

[4] Wu H M. Investigations of wheel/rail interaction on wheel flange climb derailment and wheel/rail profile compatibility[D]. Chicago: Illinois Institute of Technology. The Graduate College, 2000: 62-70.

[5] 张剑, 温泽峰, 孙丽萍, 等. 基于钢轨型面扩展法的车轮型面设计[J]. 机械工程学报, 2008, 44(3): 44-49.

ZHANG Jian, WEN Zefeng, SUN Liping, et al. Wheel profile design based on rail profile expansion method[J]. Chinese Journal of Mechanical Engineering, 2008, 44(3): 44-49.

[6] Santamaria J, Herreros J, Vadillo E G. Design of an optimized wheel profile for rail vehicles operating on two-track gauges[J]. Vehicle System Dynamics, 2013, 51(1): 54-77.

[7] 崔大宾, 李立, 金学松, 等. 基于轮轨法向间隙的车轮踏面优化方法[J]. 机械工程学报, 2009, 45(12): 205-211.

CUI Dabin, LI Li, JIN Xuesong. Numerical optimization technique for wheel profile considering the normal gap of the wheel and rail[J]. Chinese Journal of Mechanical Engineering, 2009, 45(12): 205-211.

[8] 崔大宾, 李立, 金学松, 等. 铁路钢轨打磨目标型面研究[J]. 工程力学, 2011, 28(4): 178-184.

CUI Dabin, LI Li, JIN Xuesong. Study on rail goal profile by grinding[J]. Engineering Mechanics, 2011, 28(4): 178-184.

[9] 赵伟, 王春艳, 张军, 等. 有轨电车轮轨型面匹配问题的研究[J]. 铁道学报, 2011, 32(2): 34-37.

ZHAO Wei, WANG Chunyan, ZHANG Jun, et al. Research on matching of railway wheel and rail profiles[J]. Journal of China Railway Society, 2011, 32(2): 34-37.

[10] 成棣, 王成国, 刘金朝, 等. 2种响应面方法在车轮踏面优化中的应用分析比较[J]. 中国铁道科学, 2010, 31(3): 64-68.

CHENG Di, WANG Chengguo, LIU Jinzhao, et al. Application analysis comparison of two surface methods for the optimization of the wheel tread[J]. China Railway Science, 2010, 31(3): 64-68.

[11] 李霞, 温泽峰, 张剑, 等. 轨底坡对轮轨滚动接触行为的影响[J]. 机械强度, 2009, 31(3): 475-480.

LI Xia, WEN Zefeng, ZHANG Jian, et al. Effect of rail cant on wheel/rail rolling contact behavior[J]. Journal of Mechanics Strength, 2009, 31(3): 475-480.

[12] 王文健, 郭俊, 刘启跃. 轨道参数对轮轨滚动接触行为的影响[J]. 四川大学学报(工程科学版), 2011, 42(6): 213-218.

WANG Wenjian, GUO Jun, LIU Qiyue. Effects of track parameters on rolling contact behavior of wheel-rail[J]. Journal of Sichuan University (Engineering Science Edition), 2011, 42(6): 213-218.

[13] 陈嵘, 王平, 李成辉. 75 kg/m钢轨12号重载道岔服役性能优化分析[J]. 铁道科学与工程学报, 2011, 8(6): 7-11.

CHEN Rong, WANG Ping, LI Chenghui. Optimization of service performance of No.12 heavy haul railway turnout with 75 kg/m rail[J]. Journal of Railway Science and Enginerring, 2011, 8(6): 7-11.

[14] 郭俊, 温泽峰, 金学松, 等. 钢轨三维弹塑性滚动接触应力[J]. 西南交通大学学报, 2007, 42(3): 262-268.

GUO Jun, WEN Zefeng, JIN Xuesong, et al. Three-dimensional elastic-plastic rolling contact stresses in rail[J]. Journal of Southwest Jiaotong University, 2007, 42(3): 262-268.

(编辑  陈灿华)

收稿日期：2013-08-30；修回日期：2013-10-18

基金项目：国家自然科学基金资助项目(51078320)；铁道部科技研究开发计划项目(2011G009，2012G013-A)

通信作者：曾晓辉(1982-)，男，湖南邵阳人，博士，讲师，从事高速铁路无砟轨道CA砂浆的研究；电话：028-87601210；E-mail：zxhzlh@126.com