Trans. Nonferrous Met. Soc. China 23(2013) 1046-1051
Fractal dimension for porous metal materials of FeCrAl fiber
Jian-zhong WANG1,2, Zheng-ping XI1, Hui-ping TANG1, Wei-dong HUANG2, Ji-lei ZHU1, Qing-bo AO1
1. State Key Laboratory of Porous Metal Materials, Northwest Institute for Nonferrous Metal Research, Xi’an 710016, China;
2. School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China
Received 9 March 2012; accepted 30 September 2012
Abstract: The FeCrAl fiber was used to prepare porous metal materials with air-laid technology, and then followed by sintering at 1300 °C for a holding period of 2 h in the vacuum. In addition, a novel fractal soft, which was developed based on the fractal theory and the computer image processing technology, was explored to describe the pore structure of porous metal materials. Furthermore, the fractal dimension of pore structure was calculated by the soft and the effects of magnification and porosity on fractal dimension were also discussed. The results show that the fractal dimension decreases with increase in the magnification, while it increases continuously with the porosity enhancing. The interrelationship between the fractal dimension and the magnification or porosity can be presented by the equation of D=α0exp(-x/α1)+α2 and D=k2-(k1-k2)/[1+exp((θ-k0)/k3)], respectively.
Key words: porous metal materials; FeCrAl fiber; fractal dimension; porosity; magnification
1 Introduction
Rapid development of advanced technologies in various industrial fields demands gradually structure-functional porous metal materials, especially porous fibrous materials. Metal fibers see wide applications such as wearable computers, composite materials, electromagnetic shielding or anti-static textiles, sound absorption or heat transfer parts, and high temperature filters [1]. However, the performance of these products depends on the pore structure of porous metal materials, so the accurate description of pore structure has been a hot topic in the world [2]. In order to obtain a quantitative description about complex porous structure, a large number of methods, stereological techniques and automatic image analysis, have been used for measuring porous structure parameters [3]. But a specific index is not provided to quantitatively analyze in these techniques mentioned above.
The fractal theory is a very effective tool to study the porous structure. Since the fractal theory was introduced, it has been widely applied to many fields of modern science, such as primary phase morphology [4], surface or fracture morphology [5,6], metal alloy matrix composites [7], permeability of porous media [8,9], crack detection [10], soil structure [11], frictional signals [12], internal structure and setting of flocs formed in lime softening process [13], surface structure of non-woven fabrics [14] and relationship between anatomy structure and impact energy [15], especially in describing the disorder and stochastic pore structure of porous metal materials [2,16]. The key quantity in fractal geometry is the fractal dimension; however, these investigations did not involve the evolution of fractal dimension. Additionally, the fractal dimension can be influenced by many factors, such as magnification of image and porosity of sample, and every factor may lead to its inaccurate calculation. Up to date, seldom references reported the research results studied in this aspect, so it is needed to analyze the impacting factors to fractal dimension.
In the study, porous metal materials of FeCrAl fiber were prepared by the air-laid technology in a vacuum furnace. The effects of the magnification of image and the porosity of sample on fractal dimension were then discussed. The results obtained in the work can be used to analyze the dimensionless interzone of porous metal materials, and to study the interrelationships between the fractal dimension and the properties of porous metal materials.
2 Experimental
2.1 Preparation of samples
In the study, the FeCrAl fiber with a diameter of 20 μm was used to manufacture porous metal materials. The producing process consisted in steps in: 1) short fiber, which was about 20 mm for the length, was made by stretch-breaking process; 2) metal fiber felt was made by air-laid method; 3) the felt was sintered at 1300 °C in vacuum (the vacuum of 10-2-10-3 Pa) for 2 h. The porosities of samples were tested by Archimedes’ law and the scanning electron microscopy (SEM) was performed on the polished samples to observe the microstructure. Images of FeCrAl fiber and its felt are shown in Fig. 1(a) and Fig. 1(b), respectively.

Fig. 1 SEM images of FeCrAl fiber (a) and its felt (b)
2.2 Calculation of fractal dimension
The key parameter in fractal geometry is the fractal dimension, D, which follows the scaling law [17,18]:
M(L) ~ LD (1)
where M is the length of a line or the area of a surface or the volume of an object, ‘~’ is regarded as ‘scales as’.
Equation (1) implies the characterization of self-similarity and indicates that the fractal dimension keeps constant over a range of length scales, L. Some geometry structures, such as Kock curve, Sierpinski gasket and Sierpinski carpet, appear exact self-similarity [19]. Nevertheless, a lot of objects found in nature are not exactly self-similar, while they are statistically self-similar. Statistical self-similarity means that these objects appear self-similarity over a certain local range of length scales relevant to the problem [17,20].
To calculate the fractal dimension of a two-dimensional object, such as the SEM image obtained, it can be divided into N(l) smaller self-similar squares and each is measured by the side length, l. Therefore, the fractal dimension, D, can be defined as [21]
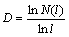 (2)
(2)
In the work, the characterization of porous structure was analyzed using a novel fractal soft which was developed based on the fractal theory and the computer image processing technology. The soft contained two parts, image processing and calculation. The image processing was composed of following steps: 1) the original image (Fig. 1(b)) was transferred into gray-scale one, then followed with de-noise and filtering shown in Fig. 2(a); 2) the dynamic threshold segmentation technology was applied to segment and the binary image was obtained as exhibited in Fig. 2(b), where the pore presented the black area and the metal fiber exhibited the gray one; 3) Figure 2(b) was divided by grid as appeared in Fig. 2(c); 4) the pore boundary of Fig. 2(c) was extracted as shown in Fig. 2(d). Calculation of the soft involved the fractal dimension, the maximum pore size, the average pore size, the porosity, the pore perimeter and its area, etc.
In the work, equation (2) was used to calculate the fractal dimension. The fractal dimension was usually estimated as the absolute value of the slope of a linear fit for data on a 1n N(l)—1nl plot which was not an integer.

Fig. 2 SEM images showing processing procedures of novel fractal soft for image filtration (a), image binaryzation (b), image division by grid (c) and pore boundary extraction (d)
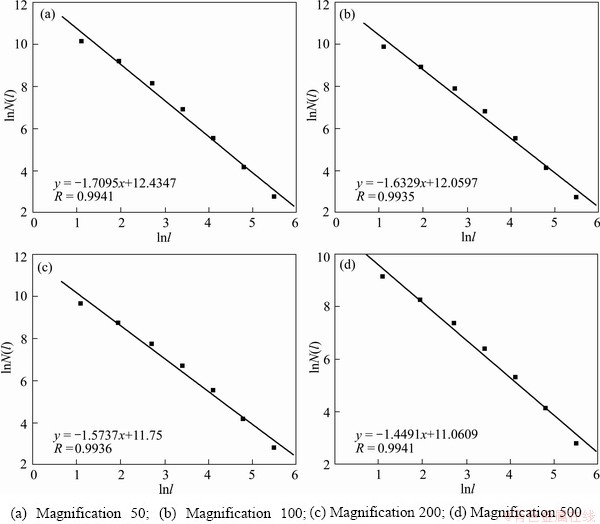
Fig. 3 Fractal dimensions at different magnifications for porosity of 97%
3 Results and discussion
3.1 Effect of magnification on fractal dimension
The fractal dimensions at different magnifications for the porosity of 97% are shown in Fig. 3. It can be seen from Fig. 3 that 1nN(l) and 1nl satisfy a very good linear relationship and all the correlation coefficients exceed 99%, so the material has very obvious fractal characteristics. Furthermore, it also can be seen from Fig. 3 that the fractal dimension decreases with increase in the magnification. The fractal dimension decreases from 1.7095 (Fig. 3(a)) to 1.4491 (Fig. 3(d)) when the magnification increases from 50 to 500. As the magnification increases continuously, the number of pore decreases slowly in an unit area for an image and the boundary of pore becomes clear, hence the fractal dimension decreases gradually.
To reveal the quantitative relationship between the fractal dimension and the magnification, the experimental results were fitted and presented in Fig. 4 for the porosities of 85%, 91%, 94% and 97%. It can be found from Fig. 4(a) that the fitting curve accords with the experimental results and the correlation coefficient exceeds 99% and the fitting curve can be defined as the exponential decay model, so do the fitting curves for Fig. 4(b), Fig. 4(c) and Fig. 4(d). The fitting curve can be expressed as D=0.3exp(-x/167.8)+1.36 for Fig. 4(a), D=0.38exp(-x/160.6)+1.36 for Fig. 4(b), D=0.4exp(- x/140.7)+1.4 for Fig. 4(c) and D=0.37exp(-x/245.7)+1.4 for Fig. 4(d). To sum up, the interrelationship between the fractal dimension and the magnification can be described by the equation of D=α0exp(-x/α1)+α2, where x is the magnification of pore structure, α0, α1 and α2 are related coefficients.
3.2 Effect of porosity on fractal dimension
The effect of porosity on fractal dimension is shown in Fig. 5. It can be seen that the fractal dimensions increase gradually with the porosities enhancing. As the porosity increases continuously, the number of pores increases slowly in a unit area for an image and the boundary of pore becomes more complex, therefore the fractal dimension increases gradually. In addition, the changing trend can be described very well using the fitting curve expressed by Boltzmann model, D=1.72-0.15/[1+exp((θ-91)/2.1)] for Fig. 5(a), D=4.47- 2.94/[1+exp((θ-117.11)/6.1)] for Fig. 5(b) and D=1.69- 0.26/[1+exp((θ-96.5)/2.9)] for Fig. 5(c). Therefore, the interrelationship between the fractal dimension and the porosity can be defined as the equation of D=k2-(k1-k2)/[1+exp((θ-k0)/k3)], where θ is the porosity of specimen, k0, k1, k2 and k3 are related coefficients.
4 Conclusions
1) The fractal dimension decreases with increase in the magnification, while it increases continuously with the porosity enhancing.
2) The interrelationship between the fractal dimension and the magnification can be described as D=α0exp(-x/α1)+α2.
3) The interrelationship between the fractal dimension and the porosity can be defined as D=k2-(k1-k2)/[1+exp((θ-k0)/k3)].
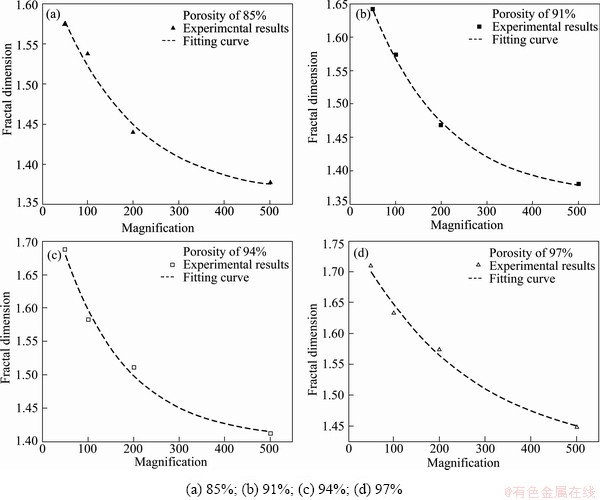
Fig. 4 Fractal dimension vs magnification for different porosities
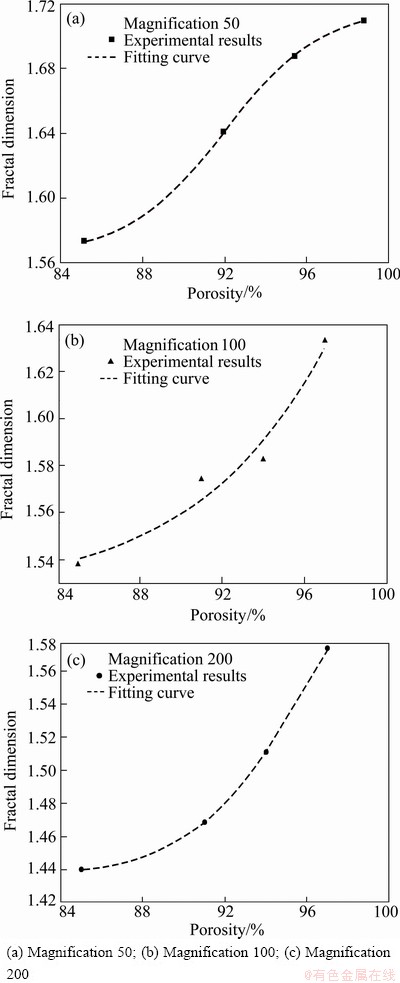
Fig. 5 Fractal dimension vs porosity at different magnifications
References
[1] HUH Y, HA B K, KIM J S. Dieless drawing steel wires using a dielectric heating method and modeling the process dynamics [J]. Journal of Materials Processing Technology, 2010, 210(13): 1702-1708.
[2] TANG H P, ZHU J L, XI Z P, DI X B, WANG J Y, AO Q B. Impact factors of fractal analysis of porous structure [J]. Science China: Technological Sciences, 2010, 53(2): 348-351.
[3] DATHE A, EINS S, NIEMEYER J. The surface fractal dimension of the soil-pore interface as measured by image analysis [J]. GEODERMA, 2001, 103(1-2): 203-229.
[4] LIU Zheng, MAO Wei-min, LIU Xiao-mei. Effect of pouring temperature on fractal dimension of primary phase morphology in semi-solid A356 alloy [J]. Transactions of Nonferrous Metals Society of China, 2009, 19(5): 1098-1103.
[5] CARRIAZO J G, MOLINA R, MORENO S. Fractal dimension and energetic heterogeneity of gold-modified Al-Fe-Ce pilc’s [J]. Applied Surface Science, 2008, 255(5): 3354-3360.
[6] DLOUHY I, STRNADEL B. The effect of crack propagation mechanism on the fractal dimension of fracture surfaces in steels [J]. Engineering Fracture Mechanics, 2008, 75(3): 726-738.
[7] WANG Liang, WANG Li-dong, FEI Wei-dong. Fractal analysis of fracture surfaces in aluminum borate whisker-reinforced aluminum alloy 6061 composite [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(3): 461-466.
[8] CHEN Yong-ping, SHI Ming-heng. Determination of permeability for porous media using fractal theory [J]. Journal of Tsinghua University: Science & Technology, 2000, 40(12): 94-97. (in Chinese)
[9] LIU Xiao-li, LIANG Bing, XUE Qiang. Fractal description of porous media permeability [J]. Advances in Water Science, 2003, 14(6): 769-773. (in Chinese)
[10] HADJILEONTIADIS L J, DOUKA E. Crack detection in plates using fractal dimension [J]. Engineering Structures, 2007, 29(7): 1612-1625.
[11] CARUSO T, BARTO E K, SIDDIKY M R K, SMIGELSKI J, RILLIG M C. Are power laws that estimate fractal dimension a good description of soil structure and its link to soil biological properties [J]. Soil Biology & Biochemistry, 2011, 43(2): 359-366.
[12] ZHU H, GE S R, CAO X C, TANG W. The changes of fractal dimensions of frictional signals in the running-in wear process [J]. Wear, 2007, 263(7-12): 1502-1507.
[13] VAHEDI A, GORCZYCA B. Application of fractal dimensions to study the structure of flocs formed in lime softening prcoesss [J]. Water Research, 2011, 45(2): 545-556.
[14] GAO Gui, ZHONG Hong-jie, SONG Xin-ju, LIU Xiang-yong, MI Xin-qiang. Fractal characteristic analysis of non-woven fabrics [J]. Journal of Tianjin Polytechnic University, 2005, 24(2): 86-88. (in Chinese )
[15] KONAS P, BUCHAR J, SEVERA L. Study of correlation between the fractal dimension of wood anatomy structure and impact energy [J]. European Journal of Mechanics-A/Solids, 2009, 28(3): 545-550.
[16] KONG J, XU C P, LI J L, CHEN W, HOU H Y. Evolution of fractal features of pores in compacting and sintering process [J]. Advanced Powder Technology, 2011, 22(3): 439-442.
[17] YU B M, LI J H. Some fractal characters of porous media [J]. Fractals, 2001, 9(3): 365-372.
[18] PITCHUMANI R, RAMAKRISHNAN B. A fractal geometry model for evaluating permeabilities of porous preforms used in liquid composite molding [J]. International Journal of Heat and Mass Transfer, 1999, 42(12): 2219-2232.
[19] CHU Wu-yang, SU Yan-jing, GAO Ke-wei, et al. Fractal in materials science [M]. Beijing: Chemical Industry Press, 2004: 166-182. (in Chinese)
[20] PITCHUMANI R, YAO S C. Correlation of thermal conductivities of unidirectional fibrous composites using local fractal techniques [J]. Transactions of the ASME: Journal of Heat Transfer, 1991, 113(4): 788-796.
[21] FAN L W, HU Y C, TIAN T, YU Z T. The predication of effective thermal conductivities perpendicular to the fibres of wood using a fractal model and an improved transient measurement technique [J]. International Journal of Heat and Mass Transfer, 2006, 49(21-22): 4116-4123.
FeCrAl纤维多孔材料的分形维数
王建忠1,2,奚正平1,汤慧萍1,黄卫东2,朱纪磊1,敖庆波1
1. 西北有色金属研究院 金属多孔材料国家重点实验室,西安 710016;
2. 西北工业大学 材料科学与工程学院,西安 710072
摘 要:利用气流铺毡技术和真空烧结炉制备了FeCrAl纤维多孔材料,其烧结温度为1300 °C,保温时间为2 h。采用基于分形理论和计算机图像处理技术自主研发的一种新型分形软件对其孔结构进行描述,计算孔结构的分形维数,研究了放大倍数与孔隙度对分形维数的影响规律。研究表明,分形维数随着放大倍数的增加而降低,随着孔隙度的增大而增大。分形维数和放大倍数、孔隙度之间的关系可以分别表示为D=α0exp(-x/α1)+α2和D=k2-(k1-k2)/[1+exp((θ-k0)/k3)]。
关键词:金属多孔材料;FeCrAl纤维;分形维数;孔隙度;放大倍数
(Edited by Hua YANG)
Foundation item: Project (2011CB610302) supported by the National Basic Research Program of China; Projects (51074130, 51134003) supported by the National Natural Science Foundation of China; Project (20110491699) supported by the National Science Foundation for Post-doctoral Scientists of China
Corresponding author: Jian-zhong WANG; Tel: +86-29-86231095; Fax: +86-29-86264926; E-mail: wangjz20012001@163.com
DOI: 10.1016/S1003-6326(13)62565-0