Trans. Nonferrous Met. Soc. China 22(2012) 604-607

X-ray peak profile analysis of dislocation type, density and

crystallite size distribution in cold deformed Pb-Ca-Sn alloys

F. ABOUHILOU, A. KHEREDDINE, B. ALILI, D. BRADAI

Faculty of Physics, University of Sciences and Technology Houari Boumediene, BP 32 El-Alia, Algiers, Algeria

Received 16 June 2011; accepted 9 August 2011

Abstract: The density, nature of the dislocations and distribution of the domain sizes in cold-deformed Pb-Ca-Sn solid solution were determined by X-ray diffraction profile analysis. The dislocation densities are of the order of 10¹⁰ cm^-2. The strain broadening of diffraction profiles was accounted for by dislocation contrast factor. The coherent domain size was determined by the recently developed PM2K software package. Assuming that the domain size distribution is log-normal, the distribution function (median μ and variance σ) was calculated from the size parameters determined from X-ray diffraction profile analysis.

Key words: Pb-Ca-Sn alloy; cold work; X-ray diffraction profile analysis (XRDLPA); PM2K software

1 Introduction

During the last decades, the increasing market for maintenance-free batteries promoted the development of the Pb-Ca-Sn alloys. These alloys showed better mechanical and electrochemical properties and were progressively replacing the Pb-Sb alloys for the manufacturing of grids. The different processes of the grid production (gravity casting, continuous casting, rolling expansion and casting expansion) generate a moderate to severe deformation levels in the microstructure [1]. The level of these deformations is the key factor determining the evolution of the morphology and the kinetics of the phase transformations that can occur during the lifetime of the grids [2].

Neutron diffraction (ND), transmission electron microscopy (TEM) and recently electron back scattered diffraction (EBSD) techniques are powerful tools for the characterization of deformation microstructures and associated features. While neutron diffraction requires unique and not widely available facilities, TEM and EBSD require very fine sample preparation with a possibility of results being biased by the preparation process itself [3]. Especially, the preparation of thin foils for TEM analysis showed special difficulties.

Line profile analysis (XRDLPA) of X-ray diffraction of a specimen is shown to be a fast, easy and very reliable method to replace the three later techniques for the determination of the deformations characteristics, such as dislocation density, dislocation type, crystallite size and stacking fault probability. Recently, this approach had been applied to three binary Pb-based alloys [4-6] and yielded good qualitative and quantitative microstructural characterization. The main conclusions of the studies were that cold-working fails to introduce appreciable amount of defects in the alloys and that the main encountered dislocation type is screw one. In the present study, we use XRDLPA to determine the dislocation type, the density as well as the crystallite size distribution in a supersaturated and cold deformed ternary Pb-Ca-Sn alloy. Such an alloy shows to be difficult to analyze with TEM. The recently proposed numerical fitting procedure, the WPPM (the whole powder pattern modeling) implemented in PM2K software package [7,8], is used to determine the microstructure in terms of crystallite size distribution and the dislocation structure from X-ray diffraction patterns.

2 Experimental

2.1 Sample preparation

Specimens of Pb-0.08Ca-2Sn (mass fraction, %) alloys were cut from a master alloy furnished by an industrial company. These specimens were remelted in quartz sealed tubes. The ingots (10 mm in diameter) were subjected to a solution annealing and quenched in liquid nitrogen. They were immediately cold deformed.

The ratio of the thickness reduction was kept slightly lower than 80% to avoid a quick recrystallization [9].

The X-ray diffraction profile analysis for each sample was carried out from the flat and polished surface by XPERT-PRO PW 3040 (Phillips) X-ray diffractometer using the Cu K_α radiation operating at 40 kV and 20 mA. The 2θ Bragg angle varied from 25° to 110°. The step scan was 0.02° and the counting time per step was 4 s. Instrumental standard for instrumental broadening correction was prepared from non-deformed and fully homogenized Pb-Ca-Sn sample. The choice of such instrumental standard was justified in Ref. [10].

2.2 XRD line profile analysis

Peak profiles observed in powder diffraction pattern result from different contributions, an instrumental component (g), and a physical profile component (f), due to the microstructure of the studied material, such as size and shape of the crystalline domains, line and planar defects (See Refs. [11,12] for details). The convolution of the profile components,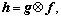yields the experimental peak profile [12].

For convenience, the WPPM algorithm adopts a Fourier analysis. In this way, a complex convolution problem is translated into the product 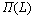 of Fourier transforms of the peak profiles produced by each separate components. According to this, the intensity in reciprocal space for the experimental profile is mathematically described by the following equation [13]:

             (1)

where d is the reciprocal space variable centred on Bragg position, L is the Fourier variable and k(d^*) contains all parameters contributing to the intensity of the peak. All contributions to the broadening enter the function 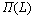. In this case, the main broadening sources are the finite size of the diffracting domains and the line and planar defects.

2.2.1 Crystallite size

The domain size effect was modelled by assuming a log-normal distribution of spherical domain sizes. In principle, one can use any distribution function appropriate to the specific study, but this choice has been proven to be effective in several cases of study [14].

A lognormal distribution is defined as [15]:

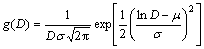             (2)

where σ² and μ are the lognormal variance and lognormal mean, respectively. The mean size of the distribution is given by:

2.2.2 Line and planar defect

Dislocation and faulting are the most common types of lattice defect that can be studied by WPPM. For dislocations, a mean dislocation density (ρ) , an effective outer cut-off radius (R_e)  and an effective edge-screw dislocation character (f_e)  can be obtained, whereas twin and deformation faults can be described by the corresponding probabilities, β and α, of finding fault along the stacking sequence [16]. Dislocations are modelled by using the Wilkens theory [17,18], where dislocations are considered to be parallel straight and randomly distributed on all equivalent slip systems. The elastic anisotropy of the dislocations, and the corresponding dependence of the profile broadening on the crystallographic direction, are accounted for by the so-called average contrast factor, 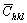. For a cubic phase, the contrast factor can be expressed as the following fourth-order invariant function of the Miller indices (hkl):

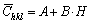                              (3)

where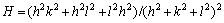and the constants A an B can be calculated from the single crystal elastic constants of the material under study, once the slip system is known.

If we assume the simultaneous presence of edge and screw dislocation, the corresponding contrast effect can be calculated as the weighted sum of the two components:

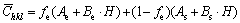       (4)

In addition to the mean dislocation density and the effective outer cut-off radius, the relative fraction of edge dislocation is also refined (as effective edge–screw dislocation character: f_e=1 for edge and f_e=0 for screw).

2.3 Whole powder pattern modelling procedure

In the method of whole powder pattern modelling, the whole measured diffraction pattern is fitted directly by the sum of the background and the theoretically constructed profile functions. These profile functions are calculated for each reflection as the convolution of the inverse Fourier transforms of the theoretically well-established size and strain Fourier coefficients and the corresponding measured instrumental profiles.

3 Results and discussion

3.1 X-ray diffractogram

Figure 1 shows a typical X-ray diffractogram of the supersaturated and cold worked Pb-0.08Ca-2Sn alloy. As it has been noticed in another Pb-based alloy [6], the effect of cold-working is small, which is evident from the widths of the peaks.

3.2 Evaluation of diffraction profiles

WPPM graphical results are shown in Fig. 2 for the Pb-0.08Ca-2Sn alloy cold deformed to 50% and 70% thickness reduction. The agreement between the experimental and modelled patterns, as shown by the residual (lower line, the difference between the experimental and modelled data), is quite satisfactory.

3.3 Grain size and diameter distribution

Figure 3 shows the grain size distribution function g(D) corresponding to the calculated μ and σ values by using the PM2K software. The median as well as the variance of the grain size decreases with the deformation rate as clearly shown with the distribution plot.

Fig. 1 X-ray diffractogram of supersaturated Pb-0.08Ca-2Sn solid solution cold worked to 70% thickness reduction

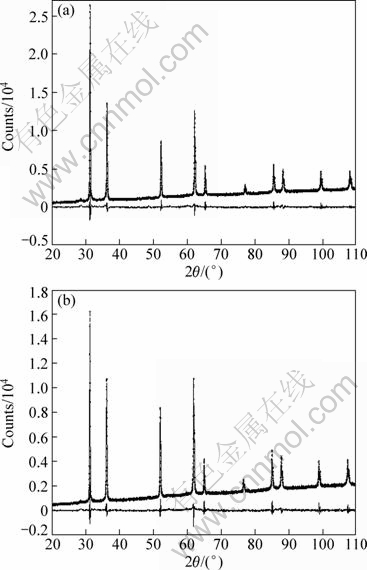
Fig. 2 Graphical output of WPPM for Pb-0.08Ca-2Sn alloy deformed to 50% (a) and 70% (b) thickness reduction. Experimental data (points) are reported together with the modelled data (line) and the residual (difference between the two) (line below)

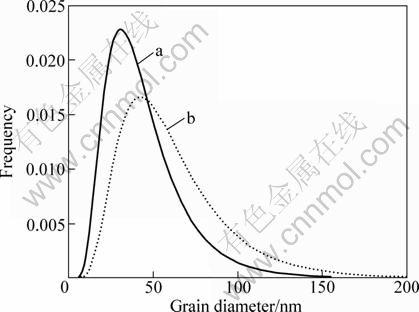
Fig. 3 Grain diameter distribution for Pb-0.08Ca-2Sn alloy cold deformed to 50% (a) and 70% (b) thickness reduction

3.4 Microstructure and lattice distortion

To estimate the dislocation, the usual {111}á110? slip system of FCC metals (Burgers vector modulus 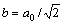, a₀ is the lattice parameter) is considered. The contrast factor for those dislocations was calculated from the single-crystal elastic constants of lead (c₁₁=48.8, c₁₂=41.4, c₄₄=14.8 GPa [19]), for both screw (s) and edge (e) dislocations in the known slip system. The corresponding constants entering Eqs. (2) and (3) are: A_s=0.2616, B_s=-2.2123, A_e=0.2517 and B_e=-1.933 [20]. Once A_e, B_e, A_s and B_s have been determined, WPPM allows one to refine the relative fraction of edge dislocations (as effective edge–screw dislocation character: f_e=1 for edge and f_e=0 for screw), in addition to the mean dislocation density and the effective outer cut-off radius. The values of dislocation densities are small and show slight strain level dependence. As pointed by CHATTERJEE et al [5], their low value may be due to an effect of recovery. However, these values are consistent with the values reported by DEY et al [6]. The dimensionless dislocation arrangement parameter M values are also presented in Table 1, where 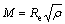[18]. This parameter characterizes the distribution and the screening of the stress and strain field of the dislocations. The value of the parameter M is less than unity, which means that the correlation (screening) between the dislocations is weak. The lattice parameter is expanded comparatively to pure Pb but is almost insensitive to strain level.

Table 1 Main WPPM results for Pb-0.08Ca-2Sn alloy cold deformed to 50% and 70% thickness reduction

The net deformation fault probability indicated that faulting only occurred. Its value decreased with strain level and was almost in the same order of the values found in other Pb-based alloys [5,6]. Such values seemed to justify a complete absence of both extrinsic and twin-fault probability in cold worked Pb-Ca-Sn at strain levels between 50% and 70% thickness reduction, thus the net deformation-faulting probability was of intrinsic nature.

4 Conclusions

1) The cold-working of supersaturated Pb-Ca-Sn alloys to strain levels ranging between 50% and 70% thickness reduction failed to introduce appreciable amount of planar defects.

2) The density of dislocations was found approximately equal to 10¹⁰ cm^-2.

3) The type of dislocations was found to be of screw type and the dislocation arrangement parameter values indicate a screening effect.

4) The size of coherent diffraction domain distribution function did not change considerably.

Acknowledgments

One of the authors A. KHEREDDINE wishes to thank heartly, Prof. M. Léoni from Trento University (Italy), for assistance and help during his stay and for kindly providing the PM2K software.

References

[1] HILGER J P. Structural hardening of lead alloys [J]. Materials and Techniques, 1993, 33: 6-7. (in French)

[2] HILGER J P. Structural hardening of lead alloys: Competition aging—Recrystallisation [J]. Journal of Physics C, 1995, 3(5): 39-48. (in French)

[3] MUKHERJEE P, SARKAR A, BARAT P, BANDYOPADHYAY S K, PINTU S, CHATTOPADHYAY S K, CHATTERJEE P, CHATTERJEE S K, MITRA M K. Deformation characteristics of rolled zirconium alloys: A study by X-ray diffraction line profile analysis [J]. Acta Mater, 2004, 52(19): 5687-5696.

[4] CHATTERJEE P, SEN GUPTA S P. Microstructural investigation of plastically deformed Pb_(1-x)Sn_x alloys: An X-ray profile-fitting approach [J]. J Appl Cryst, 1999, 32(6): 1060–1068.

[5] CHATTERJEE P, BHATTACHARYA P S, SEN GUPTA S P. Strain distributions in cold-worked-α-PbSb alloys from X-ray line profile analysis [J]. J Alloys & Comp Cryst, 1999, 284(1-2):160-165.

[6] DEY S N, CHATTERJEE P, SEN GUPTA S P. Dislocation induced line-broadening in cold-worked Pb-Bi binary alloy system in theα-phase using X-ray powder profile analysis [J]. Acta Mater, 2003, 51(16): 4669-4677.

[7] L?ONI M, CONFENTE T, SCARDI P. PM2K: A flexible program implementing whole powder pattern modelling [J]. Z Kristallogr, Suppl, 2006, 23: 249-254.

[8] SCARDI P, LEONI M. Whole powder pattern modelling [J]. Acta Cryst, 2002, 58: 190-200.

[9] HILGER J P. Hardening process in ternary lead-antimony-tin alloys for battery grids [J]. Journal of Power Sources, 1995, 53(1): 45-51.

[10] CHATTERJEE S K, HALDER S K, SEN GUPTA S P. An X-ray diffraction study of lattice imperfections in cold-worked silver-gallium (α-phase) alloys [J]. J Appl Physics, 1976, 47(2): 411-420.

[11] UNG?R T. Microstructural parameters from X-ray diffraction peak broadening [J]. Scripta Materialia, 2004, 51(8): 777-781.

[12] KLUG H P, ALEXANDER L E. X-ray diffraction procedures for polycrystalline and amorphous materials [M]. New York: Wiley, 1974.

[13] SCARDI P, LEONI M, STRAFFELINI G, de GIUDICI G. Microstructure of Cu–Be alloy triboxidative wear debris [J]. Acta Mater, 2007, 55(7): 2531-2538.

[14] LANGFORD J I, LOUER D, SCARDI P. Effect of a crystallite size distribution on X-ray diffraction line profiles and whole- powder-pattern fitting [J]. J Appl Cryst, 2000, 33: 964-974.

[15] LLOYD E. Handbook of applicable mathematics, statistics [M]. Chichester: Wiley, 1984.

[16] WARREN B E. X-ray studies of deformed metals [J]. Prog Metall Phys, 1959, 8: 147-202.

[17] WILKENS M. Fundamental aspects of dislocation theory [M]. Washington DC: National Bureau of Standards, 1970: 221-1195.

[18] WILKENS M. The determination of density and distribution of dislocations in deformed single crystals from broadened X-ray diffraction profiles [J]. Phys Stat Sol A, 1970, 2(2): 359-370.

[19] BRANDS E A, BROOK G B. Smithells metal reference book [M]. Oxford: Butterworth-Heinemann, 1992: 1089.

[20] UNGAR T, DRAGOMIR I, REVESZ A, BORBELY A. The contrast factors of dislocations in cubic crystals: The dislocation model of strain anisotropy in practice [J]. J Appl Cryst, 1999, 32: 992-1002.

冷加工变形Pb-Ca-Sn合金位错类型、密度和晶粒尺寸分布的X射线衍射峰形分析

F. ABOUHILOU, A. KHEREDDINE, B. ALILI, D. BRADAI

Faculty of Physics, University of Sciences and Technology Houari Boumediene, BP 32 El-Alia, Algiers, Algeria

摘  要：利用X射线衍射峰形分析方法，研究冷加工变形Pb-Ca-Sn合金的位错类型、密度和晶粒尺寸分布。结果表明：该合金的位错密度在10¹⁰ cm^-2数量级。衍射谱峰形的应变宽化可用位错对比因子来解释。利用新开发的PM2K软件包计算了晶粒尺寸。通过假设晶粒尺寸呈对数正态分布，利用X射线峰形分析得到的晶粒尺寸参数可得到晶粒分布函数。

关键词：Pb-Ca-Sn合金；冷加工；X射线衍射峰形分析；PM2K软件                   

(Edited by YUAN Sai-qian)

Corresponding author: A. KHEREDDINE; E-mail: khereddiney@yahoo.fr

DOI: 10.1016/S1003-6326(11)61220-X