J. Cent. South Univ. (2012) 19: 2187-2193
DOI: 10.1007/s11771-012-1263-3
A QoS-aware vertical handoff algorithm based on predictive network information
GUO Yun-song(郭云松)1, TAN Guan-zheng(谭冠政)1, A. S. M. LIBDA1, MA Li-qiang(马丽强)2
1. School of Information Science and Engineering, Central South University, Changsha 410083, China;
2. Electric Power Research Institute, Shanxi Electric Power Company, Taiyuan 030001, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: In converged heterogeneous wireless networks, vertical handoff is an important issue in radio resource management and occurs when an end user switches from one network to another (e.g., from wireless local area network to wideband code division multiple access). Efficient vertical handoff should allocate network resources efficiently and maintain good quality of service (QoS) for the end users. The objective of this work is to determine conditions under which vertical handoff can be performed. The channel usage situation of each access network is formulated as a birth-death process with the objective of predicting the available bandwidth and the blocking probability. A reward function is used to capture the network bandwidth and the blocking probability is expressed as a cost function. An end user will access the certain network which maximizes the total function defined as the combination of the reward function and the cost function. Simulation results show that the proposed algorithm can significantly improve the network performance, including higher bandwidth for end users and lower new call blocking and handoff call blocking probability for networks.
Key words: heterogeneous wireless network; vertical handoff; quality of service (QoS); birth-death process
1 Introduction
In next generation heterogeneous wireless networks, various access techniques, e.g., wireless local area networks (WLANs) and wideband code division multiple access (WCDMA), will be converged into an open wireless architecture (OWA) platform [1] and allocation of radio resources of each access network will be centralized. To make the radio resources allocated efficiently, end users may be transferred from one access network to another where vertical handoff plays an important role. In existing vertical handoff algorithms [2-5], each access network is evaluated as a value function in which there is a series of parameters such as available bandwidth, delay, and user preference. An end user will access the certain network which maximizes the value function.
Using signal-to-interference and noise (SINR) as vertical handoff criterion, a combined SINR based vertical handoff algorithm (CSVH) [6] was proposed which can provide the end users with the maximum SINR. However, the algorithm leads to network congestion due to the fact that end users always access to the network which offers the best SINR. To improve it, YANG et al [7] proposed a multi-dimensional adaptive SINR based algorithm (MASVH) to lower the number of call blocking by considering more criteria, such as user traffic cost and utilization of participating access networks. However, the utilization of networks cannot reflect the blocking situation effectively. In Ref. [8], a service history based algorithm (SHIVH) was proposed to reduce the number of handoffs and lower handoff blocking probability. However, the strategy is deployed in end users, resulting in each user only considering its own situation while ignoring the whole network situation. This leads to network congestion. An optimal distributed vertical handoff strategy [9] was proposed to describe vehicular heterogeneous networks, and NAVARRO and LIN [10] proposed an MDP-based vertical handoff decision algorithm which formulates the problem as a Markov decision process. However, algorithms in Refs. [9-10] are hard to be implemented in real system due to complexity. In Ref. [11], from the aspect of protocol layer, a explicit congestion notification based algorithm was proposed for heterogeneous networks. General trend in vertical handoff algorithms is that end users make network selection by maximizing the value function which needs a series of parameters. However, these parameters are mostly provided by the network current situation and many algorithms consider little about congestion. Thus, in the converged networks, approaches should be QoS conscious and meanwhile reduce new call and handoff call blockings effectively.
In this work, a predictive network information based vertical handoff algorithm, named PNIVH, is proposed by taking into account the predictive network information which plays a key role in offering end users higher bandwidth and lowering network call blockings. For each network, i.e., base station (BS) or access point (AP), the proposed algorithm predicts its available bandwidth and call blocking probability which are used to establish a reward function and a cost function, respectively. By combining the reward function with the cost function, a total function is established and end users are transferred to the certain network which maximizes the total function. As an extension, the cost function in our algorithm can be used to improve current network selection algorithms [4-6] in lowering call blockings. Combined with the predictive call blocking probability, the call blocking (new calls and handoff calls) [12] is reduced and the QoS of end users is guaranteed at the same time.
2 Predictive network information based algorithm
2.1 Model formulation
In heterogeneous wireless networks, an end user may experience a number of vertical handoffs during its connection lifetime and the environment considered is shown in Fig. 1, where the whole coverage area is divided into three parts: cellular coverage area, WLAN coverage area, and collocated coverage area, and the WLANs are collocated inside the coverage of a cellular system. Each end user that wishes to access the networks should establish a connection to an attachment point, i.e., a BS on the cellular network or an AP of the WLAN. It is assumed that end users periodically receive information from networks within their service area. From the network, information is broadcast via common channel, and a series of parameters including the available bandwidth and the call blocking probability are used to choose the best access network for end users. During the handoff period, the end user decides whether the user connection should use the current access network or be transferred to another network which can provide better QoS (e.g., higher throughput and lower call blockings). Due to the fact that more signaling load is brought to networks when executing handoffs, there is an important tradeoff between the QoS of the user connection and the load of network.
The channel usage problem can be formulated as a birth-death process and it is noted that the following strategy is deployed in each BS or AP. Each BS or AP has the maximum connection capacity due to the limitation of bandwidth which means that certain number of channels is provided by each BS or AP for end users. It is assumed that Cc traffic channels and Cw traffic sessions [13] are available in each BS or AP, respectively, and the number of occupied channel is considered as the system state. Thus, the state space can be written as: SBS= {0, 1, 2, 3, …, Cc}, SAP={0, 1, 2, 3, …, Cw}. Referring to Fig. 2, for each BS or AP, the sequence T={1, 2, …, t} represents successive time epoches, where the variable t denotes the current time epoch. The end user has to make a decision whenever a certain time interval has elapsed.
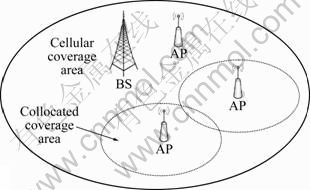
Fig. 1 Converged heterogeneous wireless networks
Fig. 2 Successive time epochs of network
At decision time epoch t, end users have to decide whether the connection should use the current access network or be rerouted to another network. This leads to the state transition which means that the number of occupied channel in a BS or an AP changes. Let N(t) denote the sytem state of time t which can be defined as: N(t)=s, s?SBS for BSs or s?SAP for APs. It is assumed that the call request arrivals obey a Poission arrival process with mean arrival rate l and the call duration is in negative exponential distribution with parameter μ [14]. Based on the nature of Poission distribution and negative exponential distribution, equations can be written as
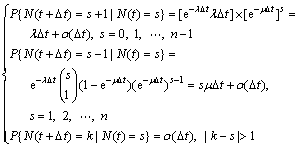(1)
where n is equal to Cc and Cw for BSs and APs, respectively. Equation (1) shows that the system state N(t) is a birth-death process [15]. Based on the birth-death process theory, the state transition diagram is shown in Fig. 3, where n is equal to Cc and Cw for BSs and APs, respectively.
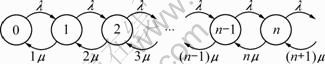
Fig. 3 State transition diagram
When time is t, let Ps(t) denote the probability that the system is in state s which can be represented as Ps(t)=P{N(t)=s}. Based on state transition diagram in Fig. 3, the differential equations of brith-death process can be defined as [16]
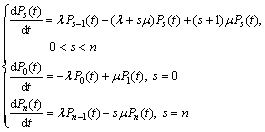(2)
where n is equal to Cc and Cw for BSs and APs, respectively.
By considering that the system is in equilibrium which means that the arrival rate and the service rate of each state s is equal to each other, Eq. (2) can be transformed as
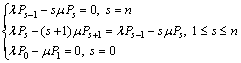(3)
By solving Eq. (3), the probability that the system is in state s can be expressed as
(4)
where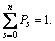 
P0 can be represented as
(5)
Let X and Y denote the system arrival rate sequence and the system service rate sequence, respectively. X and Y can be defined as X={X1, X2, …, Xt}, and Y={Y1, Y2, …, Yt}, respectively. For each BS or AP, X and Y are the history information of arrival rate and service rate which means that Xt users access the system and Yt users leave the system at certain time epoch t. Thus, by using the history information X and Y, and based on maximum likelihood estimation, the mean arrival rate l and the mean service rate m can be represented as
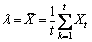(6)
(7)
For a time period (0, t), the system is considered in equilibrium with mean arrival rate l and mean service rate μ, due to the fact that the system has been running for a period. The probability Ps can be used to express the system state of each time epoch. Thus, the probability that the system is in state s in next time epoch can be predicted based on Eq. (4). This means that in next time epoch, when a new user connects to a network, the probability that the end user may be blocked can be expressed by Ps.
Finally, based on Eqs. (6) and (7), the probability that the system is in state s in next time epoch can be represented as
(8)
where s belongs to SBS and SAP for BSs and APs, respectively; n is equal to Cc and Cw for BSs and APs, respectively; k is an integer.
Due to the fact that each BS or AP has the maximum bandwidth and the bandwidth allocated to each connection will decrease when the number of user connection in a network increases, the available bandwidth can be defined as
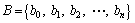
where n is equal to Cc and Cw for BSs and APs, respectively; bi denotes the system available bandwidth when i (with i=0, 1, …, n) connections are connected to network. Here, we assume that the network bandwidth is equally distributed to each user connection.
Based on Eq. (8), the probability space of next time epoch can be defined as
where n is equal to Cc and Cw for BSs or APs, respectively; Pj denotes the probability that the j-th (with j=0, 1, …, n) user is are connected to a network.
For next time epoch, the probability space defined as P is used to express the probability that a network contains a certain number of user connection. Thus, the expected available bandwidth in next time epoch can be written as
(9)
where n is equal to Cc and Cw for BSs and APs, respectively; k is an integer.
Based on the fact that a handoff connection will be blocked when the maximum capacity of a BS or an AP is reached, the probability Pn which belongs to P can be used to denote the call blocking probability, that is,
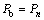(10)
2.2 Reward, cost function and handoff decision
Based on the assumption that there is one BS and one AP where the candidate BS and all APs for the end user can be indexed by 1 to 1+a, the state space sp is defined as
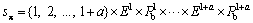
where Em and Pbm denote the expected available bandwidth and the call blocking probability of access network m (with m=1, 2, …, 1+a), respectively. At each decision time epoch, Em and Pbm can be calculated from Eqs. (9) and (10), respectively.
Given the state space sp which provides the expected available bandwidth E and call blocking probability Pb, the total function f (E, Pb) is defined as
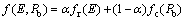(11)
where fr(E) denotes the bandwidth reward function; fc(P) denotes the handoff cost function; a is the weight factor given to the available bandwidth with 0? a ?1.
The user connection will choose the network which has higher bandwidth. Thus, the reward function can be defined as
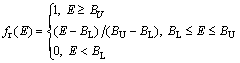(12)
where the constants BU and BL denote the maximum and minimum bandwidths required by the user connection, respectively.
During the handoff process, additional signal load will be brought to network, which means that it is a waste of network resource if an user connection is blocked. Here, the call blocking probability in state space sp is used to avoid inefficient handoffs. Specially, the handoff cost function can be defined as
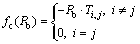(13)
where Ti,j is the switching cost from the current network i to the new network j.
At each decision time epoch, the network state space sp will be refreshed based on the information provided by the BS and each AP. By using Eq. (11) to calculate the value of each BS and AP, an end user connection will be rerouted to the certain network which has the maximum value.
2.3 System discovery and handoff trigger
As shown in Fig. 1, an end user can roam among different coverage areas. Since the cellular network is assumed to provide global coverage, the end user can always find a BS with enough level of received signal strength (RSS). When an end user locates in the collocated coverage area, it will detect the RSSs of APs and periodically receive advertisement message from networks which provide satisfied RSS. These information, such as expected available bandwidth, call blocking probability and jitter, can be used for pretreatment and network selection. Only suitable candidate networks are considered for the handoff decision.
The handoff trigger strategy is defined as j*, which can be described as: if the RSS of an AP starts decaying rapidly and falls below a threshold or the bandwidth allocated to the user connection cannot satisfy the need of the traffic, the end user will initiate vertical handoff to another network in next decision time epoch. The handoff management framework can be summarized in algorithmic as follows:
While connecting to network k
Detect the RSSs of networks.
If RSS of a network is above a certain threshold,
Receive its QoS information and store in state space sp.
If handoff is triggered based on j*,
Determine the best network i based on information in sp and Eq. (11).
If i ? k
Execute vertical handoff to network i.
Else
Remain in network k.
End
3 Extension to existing algorithms
Some vertical handoff algorithms [3-4] consider each access network as a value function with multiple parameters, e.g., available bandwidth, delay, and user preference, which can be used to choose the best network for all end users while ignoring the network congestion. This could lead to call blocking (new calls and handoff calls) which is inefficient for network performance. And in some algorithms [5-6], special schemes are deployed in vertical handoff decision process to avoid call blockings. However, it may influence QoS of the end users.
The handoff cost function mentioned above can be used to reduce call blockings and it is noted that the usage situation of bandwidth can be reflected by call blocking probability. Thus, current algorithms are combined with the handoff cost function to maintain good QoS of end users and meanwhile reduce the call blockings.
In order to combine the value functions in existing algorithms with the handoff cost function and make it effective, the value function should be normalized before it is used. In this work, exponential function is used to transform the value functions of the algorithms due to the fact that it can sensitively reflect the variation of function value. The normalized value function can be expressed as
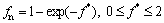(14)
where fn and f * denote the normalized value function and the value function of existing algorithm, respectively. The normalized value function is shown in Fig. 4.
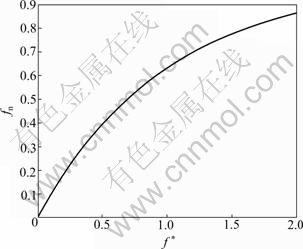
Fig. 4 Normalized value function
By taking into account the handoff cost function mentioned above, for a value function, a total function e* is defined as
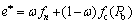(15)
where fc(Pb) is the handoff cost function defined in Eq. (13); w is a weight factor given to the value function with 0? w ?1. A certain network which maximizes the total function e* will be selected.
4 Numerical results and discussion
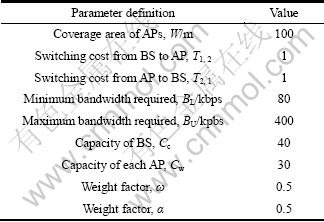
In this section, the performance of the proposed vertical handoff scheme is compared with the existing algorithms, i.e., CSVH [4], MASVH [5] and SHIVH [6]. For the purpose of evaluating the performance at the system level, a C++ based simulator was developed based on the simulator in Ref. [5]. Our system model is shown in Fig. 1. The area was 800 m ? 800 m in which there were nine APs and one BS. Our choice of cellular system was HSDPA channel and the parameters were the same as those in Ref. [5]. IEEE 802.11a standard was chosen for WLAN and the parameters in our evaluation were based on Ref. [7]. According to these parameters, the coverage area of APs was set to 100 m. The type of applications concerned in this work was data traffic, e.g., file transfer, non real-time multimedia services, and data delivery. In simulation area, 500 randomly generated end users were used, whose position changed every time interval, depending on their direction and moving speed. The user connection was randomly generated with a Poisson process and the service time was assumed to be in a negative exponential distribution with a mean connection duration of 60 s. The capacities of the BS and each AP were set to be 40 channels and 30 channels, respectively. The operation costs used for BS and each AP in algorithms [5-6] were assumed to be 0.8 and 0.4 s-1, respectively. The algorithm used in the SHIVH algorithm is MASVH. A complete list of the parameters used in the evaluation and related to the system model is given in Table 1.
Table 1 Parameters of functions and wireless networks
The new call blocking probability and handoff call blocking probability are important network indicators [10] which are evaluated by the proportion of new calls and handoff calls dropped, respectively. Firstly, the performance of our scheme is compared with existing algorithms, where we analyze the system throughtput gain, new call and handoff call blocking probability versus the arrival rate of user connection.
Figure 5 shows the system throughtput gain versus user arrival rate. The graph indicates that the proposed algorithm can always give the highest throughtput gain compared with the other algorithms and the improvement is more obvious when arrival rate increases. On the other hand, CSVH and MASVH make network selection based on the SINR and do not consider the available bandwidth in next time interval. MASVH only considers current available bandwidth by parameter named network utilization, and CSVH, by definition, does not consider available bandwidth. Thus, the usage of bandwidth is inefficient in those algorithms. Note that an increase in system throughtput gain is directly related to an increase in the allocated bandwidth of end users.
Fig. 5 System throughput gain vs user arrival rate
Figures 6 and 7 show the new call and handoff call blocking probability versus user arrival rate. It can be seen that the proposed algorithm always outperforms existing algorithms and especially, it is more effective when arrival rate increases. This is due to the fact that blockings are not be considered by CSVH while both call blockings and handoff cost are considered in our algorithm. Recall that lower call blocking means lower system handoff cost and higher QoS of end users.
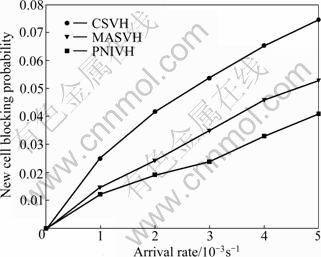
Fig. 6 New call blocking probability vs user arrival rate
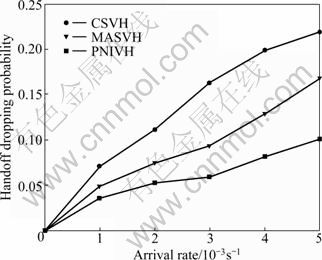
Fig. 7 Handoff call blocking probability vs user arrival rate
Secondly, the performance of the algorithms combined with our scheme is compared with the original algorithms. Three aspects are considered: system throughtput gain variation, new call and handoff call blocking probability.
Figure 8 shows the system throughtput gain variation versus user arrival rate. The system throughtput gain variation between the combined algorithm and the original one is used as vertical axis. The graph shows that the system throughtput gain of the original algorithms and the combined algorithms is almost the same, which can illustrate that the QoS of the original algorithms can be guaranteed by the handoff cost function. This is due to the fact that higher Pb means lower available bandwidth.
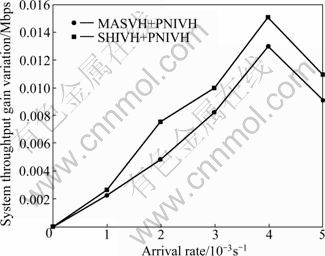
Fig. 8 System throughtput gain variation vs user arrival rate
Figures 9 and 10 show the new call and handoff call blocking probability versus user arrival rate, respectively. After combining with the proposed scheme, the algorithms can lower the call blocking probability effectively. For MASVH and SHIVH, better performances are achieved by up to 20% and 25% in terms of new call blocking and 27% and 29% in handoff call blocking probabilities, respectively. Figure 9 shows that the new call blocking probabilities of MASVH and SHIVH are almost the same due to the fact that SHIVH, by definition, is not effective in lowering new call blockings.
Figures 8-10 indicate that combined with our proposed scheme, the network performance is improved significantly in lowering call blockings and guaranteeing the QoS of end users.
Fig. 9 New call blocking probability vs user arrival rate
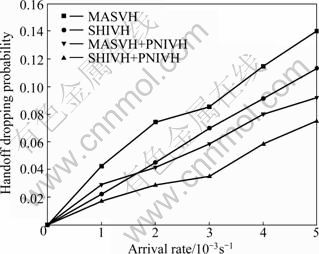
Fig. 10 Handoff call blocking probability vs user arrival rate
5 Conclusions
1) A predictive network information based algorithm is proposed for the vertical handoff decision phase. The algorithm is based on birth-death process with the objective of predicting the available bandwidth and call blocking probability to end users. A reward function is used to model the QoS of the user connection. A handoff cost function is used to model the cost of the call blockings. Our algorithm provides a tradeoff between the two important aspects which can be expressed by a total function. A certain network which maximizes the total function is selected.
2) The proposed scheme is extended from existing algorithms. Combined the cost function proposed in our algorithm, a lower new call and handoff call blocking probability is received in existing algorithms and meanwhile the QoS of end users is guaranteed.
3) For comparison, the data traffic is considered which is sensitive to bandwidth. Results show that the proposed algorithm gives a higher system throughtput and a lower new call and handoff call blocking probability which can bring higher network performance.
References
[1] HU J, LU W W. Open wireless architecture—The core to 4G Mobile communications [C]// Proceedings of IEEE ICCT. Beijing: IEEE Press, 2003: 1337-1342.
[2] ZHANG Wen-hui. Handover decision using fuzzy MADM in heterogeneous networks [C]// Proceedings of IEEE WCNC. Atlanta, GA: IEEE Press, 2004: 653-658.
[3] HE Qing. A fuzzy logic based vertical handoff decision algorithm between WWAN and WLAN [C]// Proceedings of IEEE ICNDS. Wenzhou: IEEE Press, 2010: 561-564.
[4] ALI B R, PIERRE S. On the impact of mobility and soft vertical handoff on voice admission control in loosely coupled 3G/WLAN networks [J]. IEEE Communications Letters, 2009, 13(5): 303-305.
[5] XIA Liu, JIANG Ling-ge, HE Chen. A novel fuzzy logic vertical handoff algorithm with aid of differential prediction and pre-decision method [C]// Proceedings of IEEE ICC’07. Glasgow: IEEE Press, 2007: 5665-5670.
[6] YANG Ke-meng, GONDAL I, QIU Bin. Combined SINR based vertical handoff algorithm for next generation heterogeneous wireless networks [C]// Proceedings of IEEE GLOBECOM. Washington, DC: IEEE Press, 2007: 4483-4487.
[7] YANG Ke-meng, GONDAL I, QIU Bin. Multi-dimensional adaptative SINR based vertical handoff for heterogeneous wireless networks [J]. IEEE Communications Letters, 2008, 12(6): 438-440.
[8] KIM T, HAN S W, HAN Y. A QoS-aware vertical handoff algorithm based on service history information [J]. IEEE Communications Letters, 2010, 9(10): 3000-3005.
[9] SHAFIEE K, ATTAR A, LEUNG V C M. Optimal distributed vertical handoff strategies in vehicular heterogeneous networks [J]. IEEE Journal on Selected Areas in Communications, 2011, 29(3): 534-544.
[10] NAVARRO E S, LIN Yu-xia. An MDP-based vertical handoff decision algorithm for heterogeneous wireless networks [J]. IEEE Transactions on Vehicular Technology, 2008, 57(2): 1243-1254.
[11] WANG Jian-xin, LI Jing, RONG Liang. ARROW-WTCP: A fast transport protocol based on explicit congestion notification over wired/wireless networks [J]. Journal of Central South University of Technology, 2011, 18(3): 800-808.
[12] SGORA A, VERGADOS D D. Handoff prioritization and decision schemes in wireless cellular networks: A survey [J]. IEEE Communications Surveys & Tutorials, 2009, 11(4): 57-77.
[13] KIM D K, GRIFFITH D, GOLMIE N G. A new call admission control scheme for heterogeneous wireless networks [J]. IEEE Transactions on Wireless Communications, 2010, 9(10): 3000-3005.
[14] AZHARI V S, SMADI M, TODD T D. Fast client-based connection recovery for soft WLAN-to-Cellular vertical handoff [J]. IEEE Transactions on Vehicular Technology, 2008, 57(2): 1089-1102.
[15] LU Chuan-lai. Queuing theory [M]. Beijing:Beijing University of Posts and Telecommunications Press, 2009: 34-44. (in Chinese)
[16] HE Xuan-sen. Stochastic processes and queuing theory [M]. Changsha:Hunan University Press, 2010: 65-78. (in Chinese)
(Edited by DENG Lü-xiang)
Foundation item: Project(20040533035) supported by the National Research Foundation for the Doctoral Program of Higher Education of China; Project (50275150) supported by the National Natural Science Foundation of China
Received date: 2011-11-30; Accepted date: 2012-03-10
Corresponding author: TAN Guan-zheng, Professor, PhD; Tel: +86-731-88716259; E-mail: tgz@csu.edu.cn
