恒压网络静液传动系统的神经网络滑模控制

赵立军^{1, 2, 3}，李国军¹，姜继海^{2, 3}

(1. 哈尔滨工业大学 汽车工程学院，山东 威海，264209；

2. 哈尔滨工业大学 机电工程学院，黑龙江 哈尔滨，150080；

3. 浙江大学 流体传动及控制国家重点实验室，浙江 杭州，310027)

摘要：根据恒压网络条件下的静液传动系统的特点，建立用于转速控制的二自由度动力学模型。针对恒压网络静液传动系统的参数摄动和不确定性，选择液压泵/马达的角速度和角加速度为控制变量，设计一种神经网络自适应滑模控制器，采用径向基函数神经网络(RBFNN)取代滑模切换控制部分，利用其在线学习功能，对系统的不确定因素进行自适应补偿，应用李亚普诺夫稳定性理论推导网络权值的在线自适应率，保证闭环控制系统的稳定性。在模拟试验台上进行了阶跃信号和斜坡信号的转速控制响应分析，并与常规PID控制以及基于神经网络的PID(NNPID)控制进行对比。试验结果表明：所设计的控制器具有良好的控制效果，能使系统具有良好的跟踪性和强的鲁棒性，有效地消除高频抖振现象。

关键词：恒压网络；静液传动；径向基函数神经网络；滑模变结构控制；鲁棒性

中图分类号：TH137         文献标志码：A         文章编号：1672-7207(2012)01-0137-06

Neural network sliding mode control for constant pressure hydrostatic transmission system

ZHAO Li-jun^{1, 2, 3}, LI Guo-jun¹, JIANG Ji-hai^{2, 3}

(1. School of Automobile Engineering, Harbin Institute of Technology, Weihai 264209, China;

2. School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150080, China;

3. The State Key Laboratory of Fluid Power Transmission and Control, Zhejiang University, Hangzhou 310027, China)

Abstract: A two degrees of freedom vehicle dynamic model was set up for speed control according to the characteristics of constant pressure hydrostatic transmission system. Then selecting angular velocity and angular acceleration of hydraulic pump/motor as the control variables, a novel neural network sliding mode control strategy was proposed, which was applied to ensure tracking capability to constant pressure hydrostatic transmission system in the presence of plant parameter variations and uncertainties. A radial basis function neural network (RBFNN) was utilized to realize the corrective control of sliding mode control, and compensate uncertainties of the system with adaptive learning algorithm, the parameter on-line adaptive laws were derived in the sense of Lyapunov stability theorem to guarantee the system stability. The speed control and response analysis of step signal and ramp signal were conducted in the simulation test platform, and contrasted with the conventional PID control and the PID based on the neural network (NNPID) control. The experimental results show that the proposed control scheme has good tracking performance and strong robustness, and eliminates chattering effectively.

Key words: constant pressure; hydrostatic transmission; radial basis function neural network; sliding mode control; robustness

日益严峻的能源和环境问题，凸显研发高性能的环保车辆的重要性。在大功率的平台运输车、平板车及飞机牵引车等平板运输类特种车辆中，采用基于恒压网络和二次调节技术的静液传动系统作为底盘的支撑技术，可以实现制动能的回收利用，并调整发动机的工作点，从而降低燃油消耗、减少排放，因而具有重要的理论研究价值和应用前景^[1]。但是，该系统具有参数不确定性、非线性、时变性等待征，难以建立精确的数学模型，运用经典控制和基于准确模型的控制方法，难以获得理想的控制性能^[2]，实际应用仍有较大的困难。目前，国内外在该方面的研究，主要集中于系统模型的构建与性能仿真分析；并且，为控制系统建模和分析方便，常将二次元件(液压泵/马达)的变量调节系统简化为单闭环结构，与实际系统结构有较大差别，造成分析不够准确。为此，本文将该系统按照双闭环结构进行构建。滑模控制(SMC)作为一种非线性控制，具有响应快速、对参数变化及扰动不灵敏和易于实现等优点^[3]。难点在于，变结构控制中用于处理不确定因素的切换控制，会使系统产生高频抖振现象，从而影响控制的准确性，增加能量消耗；而且，系统中的高频未建模动态容易被激发，由此破坏系统的性能，甚至产生振荡或失稳，损坏控制器部   件^[4]。人工神经网络可以用来逼近任意复杂的非线性系统，并且具有良好的自适应性和联想功能，将二者有机结合，可以有效减少滑模控制的抖振；同时，滑模控制可以提高神经网络学习的收敛速度，使系统的控制性能得到提高。本文作者针对恒压网络静液传动系统，进行径向基函数(RBF)神经网络滑模控制方法研究。利用RBF神经网络在线估计系统的不确定动力学，采用李亚普诺夫稳定性理论推导网络权值的在线自适应律，最后进行试验验证。旨在推进恒压网络下液压驱动控制技术在特种车辆中的应用基础研究。

1  系统模型

恒压网络静液传动系统的速度控制结构框图如图1所示。电流信号通过控制器处理后送入电液伺服阀，控制变量油缸活塞的移动来改变斜盘倾角，从而调节液压泵/马达(二次元件)的输出转矩和转速，进而驱动/制动车辆^[5]。关于静液传动系统的研究，为建模和控制方便，多采用单闭环结构的转速控制；但是单闭环的系统阻尼较小，系统刚度小，动态特性较差。为此，加入变量控制油缸反馈构成双闭环控制，以提高系统响应时间，减小系统的超调量，改善系统的动态控制特性^[6]。

首先作如下假设：(1) 系统没有液压油的泄露；(2) 液压油为不可压缩流体；(3) 车辆所受的空气阻力可以忽略。则系统的二自由度动力学模型为：

       (1)

式中：p_s为系统压力，Pa；J_p/m为液压泵/马达转动部件的转动惯量，kg·m²；B为液压泵/马达的黏性阻尼系数，N/(m·s)；T_f为液压泵/马达所受外负载力矩，N·m；θ为液压泵/马达转角，rad；D_max为液压泵/马达最大排量，m³/rad；D为液压泵/马达排量，m³/rad；A为变量油缸活塞有效作用面积，m²；X_{g max}为变量油缸最大位移量，m；K_v为伺服阀流量增益，m³/(s?A)；K_p为变量油缸小闭环比例控制器增益系数；K_w为小闭环位移传感器的反馈系数，V/m；r为车轮半径，m；β为坡道角，rad；f为滚动阻力系数；m为动力通道分担驱动的车辆质量，kg；d为旋转质量换算系数。因系统中使用轮边减速装置，故不考虑速比变化。

对上述方程进行拉式变换后，得恒压网络静液传动车辆的开环速度控制方框图如图2所示^[7]。

取状态变量：，x₁和x₂分别为液压泵/马达的输出角速度和角加速度，可得系统的状态方程为：

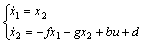         (2)

式中：；； ；；； ；。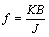

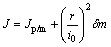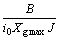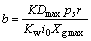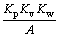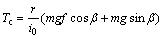图1  恒压网络静液传动系统的速度控制结构框图

Fig.1  Diagram of hydrostatic transmission velocity control system

图2  速度系统开环方框图

Fig.2  Open-loop block diagram of speed system

在车辆驱动/制动工况下，系统的压力p_s并非恒定，外负载干扰扭矩也随着路面的坡度、加减速而发生变化；系统的流量系数、泄漏系数也具有不确定性，且随着工作状态、温度等而缓慢变化^[8]，从而使系统呈现出强的非线性。本文控制的目标是：使系统能够克服上述不确定因素的影响，具有良好的跟踪性和鲁棒性。

2  神经网络滑模控制器

2.1  神经网络滑模控制器结构与原理

设计滑模控制器，是为了使被控系统满足滑模到达条件，即：使系统状态空间中的任意点必将向滑模面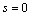靠近，并最终到达滑模面。为了获得较好的控制性能，比如提高系统状态到达滑模面的速度，常取较大的控制增益k来克服不确定性和外部扰动的影响，但会给控制系统带来不必要的抖振现象，影响系统的控制精度^[9]。为此，本文设计一种不依赖系统模型的RBF神经网络滑模控制器，将切换函数作为RBF网络的输入，滑模控制器作为RBF网络的输   出^[10]，采用RBF神经网络来估计系统的不确定动力学，控制律的参数通过系统状态信息的在线自调整获得，其结构原理如图3所示。

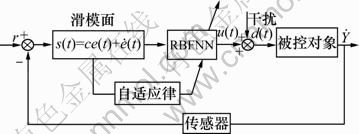
图3  神经网络滑模控制器结构图

Fig.3  Neural network sliding mode controller diagram

2.2  神经网络滑模控制器的设计

在式(2)中令

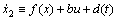            (3)

式中：f(x)为有界状态变量的函数，此处视之为未知的时变函数f(t)；b为正数；d(t)为外界干扰。

令液压泵/马达的转角位置指令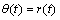，定义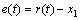为相平面变量，设计滑模面为

        (4)

其中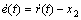：。滑动变量s将作为神经网络的输入来计算控制率u。

采用RBFNN来模拟滑动变量s和系统控制律之间的关系。RBFNN是一种三层前馈网络，本文采用的RBFNN结构为1-5-1，其结构如图4所示。神经网络的初始值为随机值，高斯函数参数取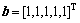，，采用persistent命令实现网络权值的更新。

在RBFNN中，高斯基函数用作径向基神经元的传递函数。其输入为滑动变量向量和高斯基函数向量的距离，即

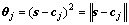             (5)

式中：s为输入的滑动变量向量；c_j为网络的第j个节点的中心向量，。输入层神经元和隐含层神经元之间的权值向量w_j设为常值1。隐含层神经元和输出层神经元之间的权值向量w_k由自适应算法进行调整。则RBFNN的输出为

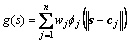            (6)

式中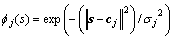：为高斯基函数；

j为隐藏层的第j个神经元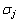；为节点j的基宽参数。n为隐含层神经元的个数。

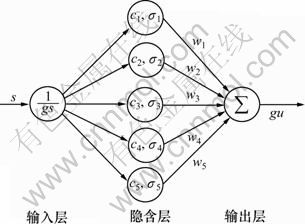
图4  RBF神经网络结构

Fig.4  RBF neural network structure

将滑模控制器设计为RBF网络的输出，即

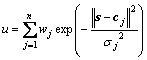           (7)

根据Lyapunov理论，滑模面的到达条件为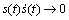，如果选取的控制律能够满足到达条件，控制系统将会趋近于相平面的原点。如上所述，RBFNN是用来逼近滑动变量s和控制律之间的非线性映射的，因而RBFNN的权值应该根据到达条件进行调整。自适应算法用来搜寻最优的权值并保证稳定性。控制的目标是使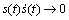，即RBF网络的权值调整指标为：

                (8)

由梯度下降法

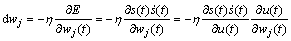  (9)

式中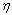：为自适应速率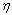，＞0。

由于

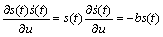
        (10)

则RBF网络权值学习自适应算法为

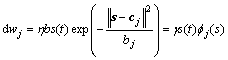   (11)

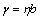其中：为学习速率，，易知。

这样，隐藏层和输出层神经元的权值就可以实时在线调整以实现RBFNN的自学习能力。

2.3  稳定性分析

采用Lyapunov方法分析所设计的控制器的稳定性。如果式(3)中的时变函数已知，则可定义精确控制律为

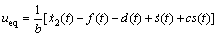    (12)

将式(12)带入式(3)，可得

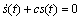             (13)

由于c是正值，因此滑动变量s会逐渐趋于0，由式(4)中切换函数的定义可知，系统的输出误差也会逐渐趋于0。RBFNN是用来逼近滑动输入变量和控制律之间的非线性函数关系的，其控制律u与精确控制率u_eq之间肯定存在误差，从而由式(3)和式(12)可得如下等式：

         (14)

理论上，RBFNN能以任意精度逼近任意连续函数。因此作如下假设：

假设 存在最优的权值向量使得控制律u和精确控制率u_eq之简单误差小于：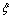

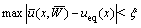         (15)

式中：，。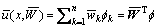

    定义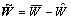为最优值和当前估计值之间的权值误差向量，则式(14)可以写为：

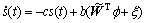        (16)

选取Lyapunov函数为：

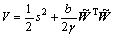              (17)

式(17)对时间求导得

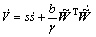              (18)

将式(11)和式(16)带入式(18)得

≤

             (19)

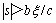则当时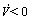，。这就意味着Lyapunov函数会逐渐减小，切换函数将会逐渐收敛到滑模面的一个很小的边界层内。由以上的分析可以得出所设计的控制器是稳定的，并且系统的误差会被控制在很小的范围内。随着神经网络非线性映射精度的提高，系统的输出误差也会降低。

3  试验验证

3.1  静液传动混合动力车辆模拟试验系统

转速控制性能试验在液压混合动力车辆的模拟试验平台上进行。试验台系统信号关系和硬件构成如图5和图6所示。将所设计的神经网络滑模控制器，利用C++ Builder语言进行编程，植入静液传动混合动力车辆的控制系统中，恒压系统工作压力为7 MPa，加载扭矩为8 N·m，进行静液传动混合动力车辆神经网络滑模控制(NNSMC)试验研究，并与常规PID控制以及基于神经网络的PID(NNPID)控制进行对比。

3.2  试验结果

图7和图8所示分别为3种控制的阶跃响应和斜坡响应试验曲线。可见：PID控制时系统超调量明显增加，且动态稳定调整时间长，系统进入稳定前振荡次数增多，稳态误差大；基于神经网络的PID控制，虽然在超调量和振荡次数上有较大改善，但其响应速度明显滞后；相对于以上两种控制方式，神经网络滑模控制基本无超调，系统进入稳定前没有振荡，响应速度快且趋近效果好。

图5  液压混合动力车辆模拟试验台构成示意图

Fig.5  Experimental system schematic diagram of hydrostatic transmission hybrid vehicle

图6  液压驱动混合动力车辆模拟试验平台实物图

Fig.6  Prototype of hydrostatic transmission hybrid system

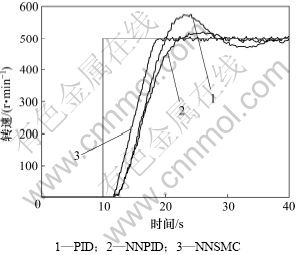
图7  阶跃转速目标下的转速控制响应对比

Fig.7  Comparison of speed control responses to step speed

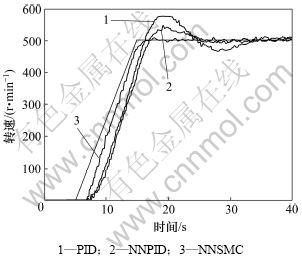
图8  斜坡转速目标下的转速控制响应对比

Fig.8  Comparison of speed control responses to slope speed

由试验结果可知：在响应速度和稳态误差以及对外界抗干扰能力方面，神经网络滑模控制效果均优于普通PID控制和基于神经网络的PID控制，具有更强的鲁棒性。

4  结论

(1) 针对恒压网络静液传动系统的转速控制过程中的参数摄动和不确定性，进行了RBF神经网络滑模控制研究。采用RBF神经网络在线估计系统的不确定动力学，利用李亚普诺夫稳定性理论推导网络权值的在线自适应律，确保闭环控制系统的稳定性，提高系统的响应速度，并达到削弱抖振的目的。

(2) 神经网络滑模控制方法对于参数扰动及负载干扰，具有较好的动态响应性能、较高的稳态控制精度和较强的鲁棒性，并能有效削弱控制信号中的高频抖振。该方法可靠易行，适于工程应用。

参考文献：

[1] Kepner R P. Hydraulic power assist: A demonstration of hydraulic hybrid vehicle regenerative braking in a road vehicle application[C]. SAE Paper, 2002-01-3128.

[2] 吴光强, 王会义. 车辆静液驱动与智能控制系统[M]. 上海: 上海科学技术文献出版社, 1998: 1-30.
WU Guang-qiang, WANG Hui-yi. Hydrostatic drive vehicle and intelligent control system[M]. Shanghai: Shanghai Scientific and Technological Literature Publishing House, 1998: 1-30.

[3] Young K D, Utkin V I, Ozguner U. A control engineer's guide to sliding mode control[J]. IEEE Transactions on Control Systems Technology, 1999, 7(3): 328-342.

[4] 刘金琨. 滑模变结构控制MATLAB仿真[M]. 北京: 清华大学出版社, 2005: 202-217.
LIU Jin-kun. Matlab simulation for sliding mode control[M]. Beijing: Tsinghua University Press, 2005: 202-217.

[5] 姜继海, 韩永刚, 王德海, 等. 二次调节静液驱动系统的智能PID控制[J]. 哈尔滨工业大学学报, 1998, 30(1): 36-38.
JIANG Ji-hai, HAN Yong-gang, WANG De-hai, et al. The intelligent PID control in hydrostatic drive system with secondary regulation[J]. Journal of Harbin Institute of Technology, 1998, 30(1): 36-38.

[6] 刘宇辉, 蒲红, 姜继海. 二次调节转速系统的双闭环控制研究[J]. 机床与液压, 2001(1): 39-40.
LIU Yu-hui, PU Hong, JIANG Ji-hai. Research on closed-loop control system of hydrostatic transmission with secondary regulation[J]. Machine Tool & Hydraulics, 2001(1): 39-40.

[7] 战兴群. 静液驱动二次调节技术控制特性的研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 1999: 31-48.
ZHAN Xing-qun. Study of control characteristics of hydrostatic driving secondary regulation technology[D]. Harbin: Harbin Institute of Technology. School of Mechatronics Engineering, 1999: 31-48.

[8] 孙辉, 姜继海, 王昕. 静液传动混合动力车辆的QFT鲁棒控制器设计[J]. 吉林大学学报: 工学版, 2009, 39(6): 1538-1543.
SUN Hui, JIANG Ji-hai, WANG Xin. Quantitative feedback robust controller design for hydrostatic transmission hybrid vehicle[J]. Journal of Jilin University: Engineering and Technology Edition, 2009, 39(6): 1538-1543.

[9] 郁明, 丛爽. 基于径向基函数神经网络滑模控制的运动控制系统[J]. 系统仿真学报, 2009, 21(3): 776-779.
YU Ming, CONG Shuang. Radial basis function neural network sliding mode control for motion control system[J]. Journal of System Simulation, 2009, 21(3): 776-779.

[10] Huang S J, Huang K S, Chiou K C. Development and application of a novel radio basis function sliding mode controller[J]. Mechatronics, 2003, 13: 313-329.

(编辑 杨幼平)

收稿日期：2011-01-15；修回日期：2011-04-28

基金项目：国家自然科学基金资助项目(50875054)；浙江大学流体传动及控制国家重点实验室开放基金资助项目(GZKF-2008003)

通信作者：赵立军(1975-)，男，辽宁北宁人，博士，副教授，从事车辆工程、流体传动与控制研究；电话：13061168554；E-mail: zhaolijun@hitwh.edu.cn