文章编号: 1004-0609(2005)06-0958-08
高岭石脱水反应的非等温热重法研究
姜 涛, 李光辉, 陈许玲, 范晓慧, 黄柱成, 邱冠周
(中南大学 资源加工与生物工程学院, 长沙 410083)
摘 要: 在系统分析非等温固相反应特点的基础上, 建立了非等温脱水反应速率方程。 采用非等温热重法、 通过计算机辅助计算, 对高岭石脱水反应动力学规律进行了研究。 结果表明: 由于高岭石晶体结构中内、 外羟基脱除的顺序不同, 其脱水反应机制在反应分数(α)为0.7左右时发生改变。 在反应前期(0〈α〈0.7)时, 脱水反应遵循二维扩散控制规律, 脱水反应表观活化能为159.682kJ/mol、 表观频率因子为1.007×1010/min。
关键词: 高岭石; 非等温热重法; 动力学; 脱水反应
中图分类号: TD985; TD927 文献标识码: A
Non-isothermal thermogravimetric investigation on kinetics of dehydroxylation of kaolinite
JIANG Tao, LI Guang-hui, CHEN Xu-ling, FAN Xiao-hui,
HUANG Zhu-cheng, QIU Guan-zhou
(School of Resources Processing and Bioengineering,
Central South University, Changsha 410083, China)
Abstract: Based on the systematical analysis of the characteristics of the non-isothermal solid-reactions, a rate equation of dehydroxylation reactions was founded. And the kinetics of dehydroxylation of kaolinite was investigated by using non-isothermal thermogravimetric method with the aid of computer. It is found that, the mechanism of dehydroxylation of kaolinite converts at the reaction fraction of 0.7, because the —OH groups in interlamellar space associated with the alumina sheets lose more easily than those in intralamellar space between the silica and alumina sheets. When the reaction fraction is below 0.7, the thermal dehydroxylation of kaolinite is found to be controlled by two-dimensional diffusion-controlled. The apparent activation energy and apparent pre-exponential Arrhenius factor of the reaction are obtained as 159.682kJ/mol and 1.007×1010/min, respectively.
Key words: kaolinite; non-isothermal thermogravimetry; kinetics; dehydroxylation
高岭石是一种具有优良物理化学性能和工艺特性的非金属矿物原料, 在陶瓷、 橡胶、 涂料、 化妆品等领域中均有广泛的用途。 随着科学技术的进步, 用高岭石作原料, 通过层间化学反应、 化学改性等深加工方法, 可制备出许多用于石油、 化工、 环保等领域的新型功能材料(如插层化合物、 催化剂、 铝盐骤合物等), 也作为新型结构陶瓷和功能陶瓷的原料用于核能、 火箭、 红外与远红外技术中[1]。
研究表明[2-6]: 热作用下高岭石要经历一个由晶态向非晶态、 再由非晶态重新向晶态转变的过程。 一定温度下的热处理可提高高岭石的活性, 同时热处理过程中高岭石所形成的具有特殊性质和结构的中间产物, 可以作为制备功能材料的母体。 因此, 对热处理过程中高岭石的稳定性、 结构变化及物相转变规律的研究具有重要的理论和实际意义, 特别是对于脱去结构水后的偏高岭石, 长程无序而近程有序的晶体结构特征, 使它拥有许多高岭石本身所没有的性质。 因此, 对偏高岭石生成过程及结构的研究广受关注。
为此, 国内外的学者结合各种测试技术对偏高岭石生成过程和结构特点开展了大量研究[7-17]。 由于偏高岭石的生成主要是由于脱羟所致, 因此也有少数学者试图通过研究热处理过程中高岭石脱水机制来进行描述[5, 18-25]。
迄今关于高岭石脱水反应机理的研究虽然不少, 但结论尚不统一。 Johnson和Keller[20]认为高岭石脱水反应属相边界控制; Brindley等[21]和Holt等[24]认为属扩散控制; 而Criado等[25]的研究指出, 只有当α≤0.6时高岭石脱水反应才遵循扩散控制机理。 另外, 在研究方法上, 虽然基本都是采用热重法, 但绝大多数是在等温过程下进行的。 由于在等温热重曲线的测试过程中, 在实验操作上难以将反应试样在实验一开始就刚好保持在所选定的温度点上, 再加上受测试仪器灵敏度的影响, 试样必须有明显的反应才能进行准确测量, 而事实上此前反应可能早已开始, 因而造成实验结果存在较大的误差。 这也是导致目前研究结果不能完全统一的主要原因之一。
考虑到非等温热重法研究反应过程动力学时, 只需测定一条热重曲线就可在反应从开始到结束的整个温度区间内连续计算动力学参数, 产生的误差小[26]。 因此, 本文作者选用非等温过程热重法, 通过编程借助于计算机来研究高岭石脱水反应动力学规律, 求取相关动力学参数。
1 非等温热重法脱水反应速率方程与研究方法
1.1 反应动力学速率方程的推导
由于经典化学动力学是建立在等温过程和均相反应的基础之上, 等温条件下建立的反应速率方程(式(1))和速率常数k与温度的关系式(式(2))不能用于非等温条件下的动力学研究中
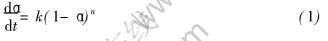
式中 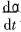 为反应速率; α为物质转变分数; n为反应级数; k为速率常数, k随温度变化的规律可用Arrhenius方程表示为
为反应速率; α为物质转变分数; n为反应级数; k为速率常数, k随温度变化的规律可用Arrhenius方程表示为
k=Aexp(-E/RT)(2)
式中 T为反应绝对温度; A为频率因子; E为反应活化能; R为理想气体状态常数。 但是, 考虑到在无限小的时间间隔内, 非等温过程可近似看成是等温过程, 而且脱水反应是一相对简单分解反应, 系统的平衡状态具有在特定温度下发生突变的特点, 属不变量型反应过程。 根据有关研究结果[26]: 不变量型非等温过程反应动力学的基本速率方程在形式上与等温过程完全类似。 因此, 只要在形式上作一定的修正后, 非等温过程反应动力学速率方程仍可用式(1)来表示。
在修正过程中, 考虑到把从气相基元反应总结而得的经典化学动力学基本理论推广到固相反应动力学研究中时, 反应体系和反应过程较之气相反应变得更加复杂, 不能用一个恒定的反应级数(n)来概括整个过程的规律性, 必须采用更一般的形式来表示, 为此, 用一个函数f(α)代替(1-α)n来表示反应所遵循的机制, 用函数k(T)来表示温度为T时的反应速率常数, 将非等温过程反应速率方程修正为:

对于f(α)的具体形式, Sestak等[26]在归纳总结已提出的各种有关这一函数表达式的模型后, 给出了其一般形式:
f(α)=αm·(1-α)n·[-ln(1-α)]p(4)
式中 对于某一具体的f(α)函数, m、 n、 p为绝对值小于1的常数, 在同一反应中只能单一出现或两两出现, 三者同时出现的方程暂无明确的物理意义。 在热重法中α为t时刻的反应分数, 可由式(5)计算而得:

式中 m0为试样在反应前的初始质量; mt为反应进行到t时刻的试样质量; m∞为反应结束时的试样质量。
对于k(T)的具体形式, 由于非等温过程中反应温度是连续变化的, 再加上脱水反应本身又是一个吸热过程, 反应温度会发生改变, 频率因子(A)不是一个恒定的数值, 所以严格地说, 此时的反应速率常数不适合于用式(2)所示的Arrhenius方程来表示。 但是, 考虑到在大多数情况下, 频率因子(A)随温度的变化对k值的影响程度, 与其后面的指数项随温度的改变对k值的影响程度相比要小得多。 所以, 本文在研究脱水动力学时, 为简化计, 仍然认为A是一个不随温度变化的常数, 反应速率方程依然满足于Arrhenius方程, 即
k(T)=A exp(-E/RT)(6)
在非等温热重实验中, 反应是在程序控制的升温速率下进行, 其升温速率(β)可表示为
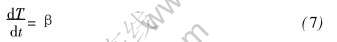
由式(3)、 (4)、 (6)和(7)可得表达形式最为一般的非等温过程动力学速率方程通式:
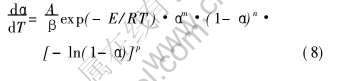
1.2 研究方法
热重法研究反应动力学最常用的数据处理方法是“试凑法”: 首先根据反应本身的特点假定该反应过程可能遵循的反应机制, 得到相应的反应速率方程; 然后将实验测得的不同时刻反应转变分数代入反应速率方程, 看它们是否能够满足方程。 如果实验数据呈线性关系, 则说明反应遵循所假定的机制。 否则, 需假定其它反应机制重复上述过程, 直到找到适宜的反应机制为止。 显然, “试凑法”在确定反应机制时具有一定的盲目性和主观性, 有时为了得到一个适宜的机制函数需要花费较多的时间。
为克服这一缺点, 文献[26]报道了一种通过计算机辅助计算来研究非等温热重法固态反应动力学的方法, 该法的基本思想是通过编写一个动力学五参数(A、 E、 m、 n、 p)搜寻程序, 由计算机来搜寻满足实验数据要求的动力学参数组合, 根据求得的参数来确定反应所遵循的规律。 本实验即采用这一方法, 通过自行编写的计算程序来研究高岭石脱水反应动力学规律, 具体的数据处理方法如下。
1) 将式(8)移项、 整理并写成求残差平方和(R)的形式:
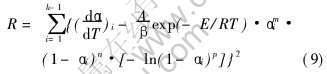
2) 采用Visual C++语言编写一套确定R值为最小的搜寻程序(程序框图如图1所示, 具体程序略)。 搜寻程序可满足如下要求: 确定R小于某一δ值(在本文中取δ为万分之一), 使计算机能按所需目标搜寻结果; 程序中(dα/dT)i的计算是按三次样条函数插值求得; 程序中m、 n、 p的取值范围确定为-1到+1之间, 并要求三者不同时出现。
3) 在同一条实验热重曲线上取K组实验数据Ti、 αi, 并输入计算机。 选定一组E、 A值代入上述搜寻程序进行计算, 如果所选定的E、 A值不符合要求, 则输入新的一组E、 A值重新计算。 如此进行, 直到找出一组或几组残差平方和(R)为很小(R〈δ)的A、 E、 m、 n、 p值, 从而初步确定一种或几种可能机制函数f(α)的形式。 必须注意的是, 经搜寻得到的结果只能定性地了解m、 n、 p的大小及相互之间的组合形式, 其最终结果还必须将具体的f(α)函数形式连同m、 n、 p进行回归分析。
4) 将式(8)移项、 整理并两边取对数得:

将搜寻得到的一组或几组m、 n、 p值所对应的机制函数具体形式, 与所取实验数据Ti、 αi以及三次样条插值计算得到的( 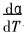 )i分别代入式(10)中作线性回归分析。 并从分析结果中找出相关系数绝大值最大的一组来, 按式(11)计算F(α)值, 并作
)i分别代入式(10)中作线性回归分析。 并从分析结果中找出相关系数绝大值最大的一组来, 按式(11)计算F(α)值, 并作 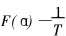 图, 求得直线的斜率和截距。
图, 求得直线的斜率和截距。
根据式(12)可知, 直线的斜率为-E/R、 截距为ln(A/β), 由此可求得反应的两个主要动力学参数即表观活化能(E)和表观频率因子(A)。
5)将m、 n、 p代入式(4)得反应机制函数, 将计算所得的全部参数A、 E、 m、 n、 p代入式(8)得到脱水反应动力学的速率方程。
2 结果与讨论
选取天然产出的高岭石矿作为实验样品, 经X射线衍射、 红外光谱等多种测试技术综合研究表明, 高岭石结晶完整, 样品主要矿物组成及含量分别为高岭石88%~90%、 α-石英7%~8%和伊利石2%~3%。
为了确定高岭石脱羟基反应的起始和终了温度, 并获得不同温度下高岭石的质量损失率, 采用
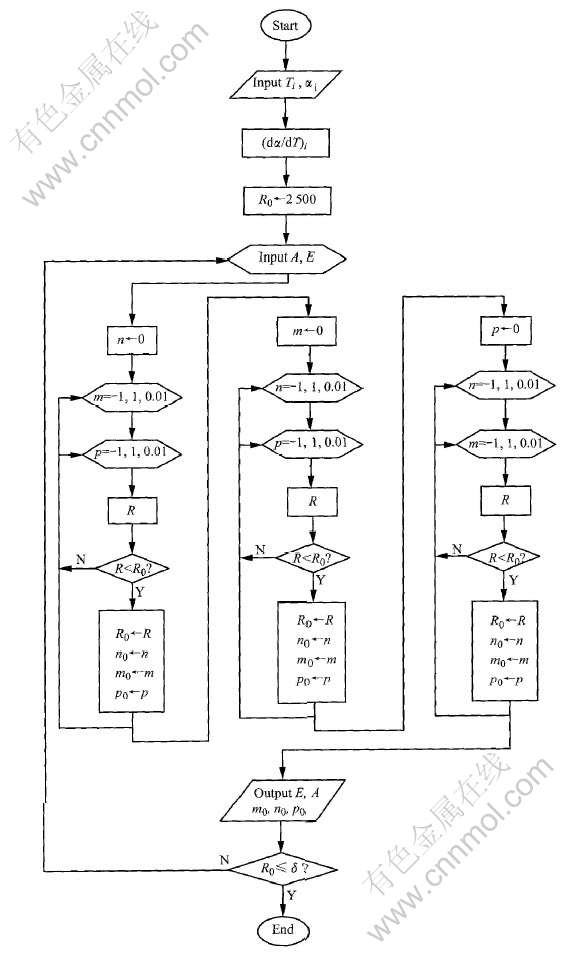
图1 非等温热重法研究固态反应动力学五参数搜寻程序框图
Fig.1 Program sketch of non-isothermal kinetics of solid-reaction investigation
日本理学TAS-100热分析仪测定了高岭石的TG曲线, 结果如图2所示。 实验时, 样品处于静止的空气中, 设定程序升温速率为10℃/min。
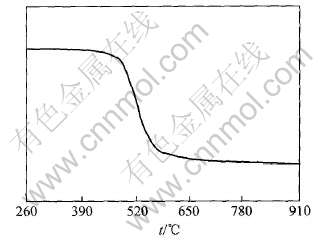
图2 高岭石的热重分析曲线
Fig.2 TGA curve of kaolinite sample
在图2所示TG曲线上, 在420~670℃的范围内产生了一个明显的质量损失台阶, 这是高岭石脱羟基作用所致, 由此可确定脱羟基反应开始和终了温度分别为420和670℃。
根据式(5)关于α的计算公式, 可由图2中TG曲线计算得到不同温度下高岭石的反应分数α, 结果如图3所示。
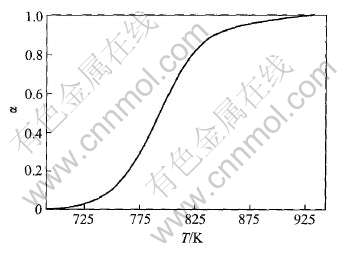
图3 高岭石脱水反应分数与温度的关系
Fig.3 Reaction fraction of kaolinite at different temperatures
分别在图3所示曲线上读取一系列数据(Ti, αi), 并全部输入非等温热重法动力学五参数搜寻程序中, 通过计算机来搜寻满足残差平方和(R)小于10-4时的A、 E、 m、 n、 p值。
但是, 在程序的搜寻过程中发现, 无论输入何种组合的A、 E值, 均不能找到满足条件R〈10-4的m、 n、 p值。 当把求得R为最小值时的一组A、 E、 m、 n、 p代入式(11)计算F(α)值, 并作F(α)—T-1图, 则发现得到的F(α)—T-1曲线图明显分为两段(如图4所示)。 因此, 回归分析时所表现出来的线性关系很差。 由此说明, 高岭石脱水反应用一个机制函数不能概括其整个过程的规律。
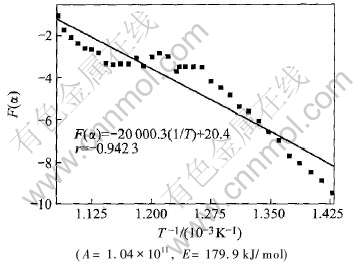
图4 F(α)—1/T的关系及其线性回归结果
Fig.4 Curve of F(α)—1/T and linear regression results(0≤α≤1)
为了确定高岭石脱水反应机理发生转变的具体范围, 分别对0≤α≤1, 0≤α≤0.9, 0≤α≤0.7, 0≤α≤0.6进行了计算。 表1给出了上述4种情况下, 当线性回归相关系数(r)绝对值达最大时, 其对应的A、 E和求得的R值。
表1 不同α取值范围下r绝对值最大时的计算搜寻结果
Table 1 Calculated results at different ranges of α and maximum absolute value of r

同样计算0≤α≤0.9, 0≤α≤0.7, 0≤α≤0.6三种情况下的F(α), 按F(α)—T-1作图并进行线性回归, 有关结果如图5~7所示。
由表1和图4~7可知, 当α的取值范围由0≤α≤1减小到0≤α≤0.9, 0≤α≤0.7时, F(α)与T-1的线性相关性逐渐变好, 线性相关系数绝大值也随之增大。 但是, 当α的取值范围减小为0≤α≤0.6时, F(α)与T-1的线性相关性相反而变差, 其
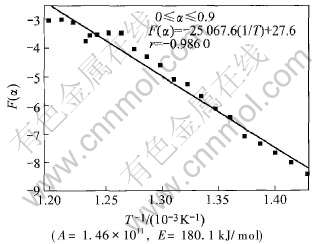
图5 F(α)—1/T的关系及其线性回归结果
Fig.5 Relationship between F(α) and 1/T and linear regression results
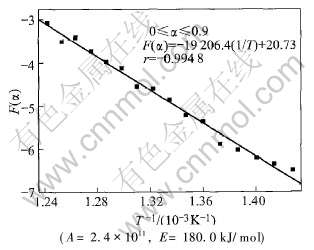
图6 F(α)—1/T关系及其线性回归结果
Fig.6 Relationship between F(α) and 1/T and linear regression results
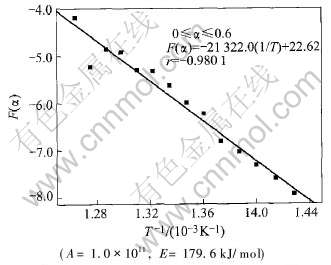
图7 F(α)—1/T的关系及其线性回归结果
Fig.7 Curve of F(α)—1/T and linear regression results
线性相关系数的绝对值最大值较0≤α≤0.7时明显减小。 由此可知, 高岭石脱水反应动力学机制应在反应分数(α)为0.7左右时发生转变。
当0≤α≤0.7时, 由程序搜寻得到五参数的值分别为: A=2.4×1011, E=180.0kJ/mol, m=0, n=0, p=-0.97。
取m=0, n=0, p=-1, 由此可得0≤α≤0.7时高岭石脱水反应的动力学机制函数为:
f(α)=[ln(1-α)]-1(13)
因此, 在0≤α≤0.7时, 即高岭石脱水反应的前期, 其反应机制为扩散控制, 并且遵循二维扩散控制规律。
根据图6所得到的有关结果进行回归分析, 可得如下线性方程:
f(α)=-19206.4T-1+20.73(14)
由回归直线的斜率和截距即可求得反应的表观活化能(E)和表观频率因子(A):
由-E/R=-19206.4, 得反应的表观活化能: E=159 682.0J/mol
由ln(A/β)=20.73, β=10K/min, 得到反应的表观频率因子(A): A=1.007×1010/min
将m=0, n=0, p=-1, A=1.007×1010/min、 E=159 682.0J/mol全部代入式(8)中, 便可得到高岭石脱水动力学的反应速率方程:
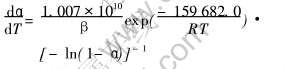
据报道[25]: 高岭石脱水反应机理分为两段, 在0≤α≤0.6左右时反应属扩散控制, 通过动力学计算求得的表观活化能(E)的范围为150~170kJ/mol, 表观频率因子(A)的数量级为1010。 通过比较后发现, 本文通过非等温热重法研究得到的有关结论与文献中的这些结果除了机制发生转变的条件稍有不同外, 其它结果完全吻合。
高岭石属二八面体1∶1型层状硅酸盐矿物, 其晶体结构是由无数氢氧铝八面体层与硅氧四面体层相结合所构成的单一分子层通过氢键作用叠加而成(图8)。 在氢氧八面体层中, 而每个Al同时和两个O和4个OH相连, Al充填在2O和4OH所形成的八面体空隙之中, 但Al只充填所有空隙数的2/3, 即Al的配位数为6。 因此, 高岭石晶体结构中3/4的羟基处于外羟基位置; 另外1/4的羟基处于内羟基位置。
文献[17]的研究结果表明: 高岭石晶体结构中内、 外羟基的脱去不同步, 外羟基较内羟基容易脱去。 虽然, 热处理过程中高岭石的脱羟基过程, 不会完全按照先失去外羟基, 再失去内羟基的顺序进行, 但有一点可以肯定, 绝大多数外羟基应先于内羟基脱去, 脱水反应机制的转变条件应接近于α=0.75。 这充分说明采用非等温热重法, 通过动力学五参数搜寻程序来研究固态反应动力学是可行的, 得到的结论是可靠的。 至于0.7≤α≤1.0条件下高岭石脱水反应所遵循的机理, 由于在该阶段高岭石的脱水反应比较复杂, 经五参数程序搜寻求得的动力学机制函数均无实际意义, 因此本文不再对其进一步进行分析研究。
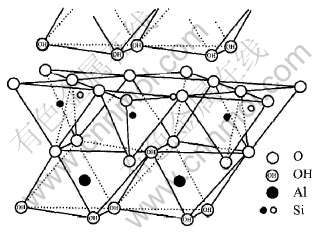
图8 高岭石晶体结构示意图
Fig.8 Crystal sketch of kaolinite
3 结论
1) 采用非等温热重法, 通过动力学五参数搜寻程序来研究固态反应动力学是可行的, 得到的结论是可靠的。
2) 由于高岭石晶体结构中内、 外羟基失去的顺序不同, 因此其脱水反应机制在脱水反应分数α=0.7左右时发生改变。
3) 对高岭石脱水反应动力学研究表明, 在脱水反应前期, 0〈α〈0.7时, 反应遵循二维扩散控制规律, 脱水反应表观活化能E=159.682kJ/mol, 表观频率因子A=1.007×1010/min。
REFERENCES
[1]Brindley G W, Nakahira M. The kaolinite-mullite reaction series(Ⅲ)—The high temperature phases[J]. J Am Ceram Soc. 1959, 42(7): 319-324.
[2]QIU Guan-zhou, JIANG Tao, LI Guang-hui, et al. Activation and removal of silicon in kaolinite by thermochemical activation[J]. Scandinavian Journal of Metallurgy, 2004, 33: 121-128.
[3]Charkraborty A K, Ghosh D K. Reexamination of the kaolinite-to-mullite reaction series[J]. J Am Ceram Soc, 1978, 61(3-4): 170-173.
[4]Mazumdar S, Mukherjee B. Structural characterization of the spinel phase in the kaolin-mullite reaction series through lattice energy[J]. J Am Ceram Soc, 1983, 66(9): 610-612.
[5]Davies T W, Slade R C T. Physical and Chemical Transformations of Kaolinite Caused By Flash Calcination(Series E: Applies Science)[M]. Davies: Kluwer Academic Publishers, 1995. 73-94.
[6]LIU Kuo-chung, Thomas G. Time-temperature-transformation curves for kaolinite-α-alumina[J]. J Am Ceram Soc, 1994, 77(6): 1545-1552.
[7]Percival H J, Duncan J F. Interpretation of the kaolinite-mullite reaction sequence from infrared absorption spectra[J]. J Am Ceram Soc, 1974, 57(2): 57-61.
[8]Bulens M, Leonard A, Delmon B. Spectroscopic investigations of the kaolinite-mullite reaction sequence[J]. J Am Ceram Soc, 1978, 61(1-2): 81-84.
[9]Temuujin T, Okada K, Mackenzie K J D, et al. The effect of water vapour atmosphere on the thermal transformation of kaolinite investigated by XRD, FTIR and solid state MAS NMR[J]. J European Ceram Soc, 1998, 19: 105-112.
[10]Percival H J, Duncan J F, Foster P K. Interpretation of the kaolinite-mullite reaction sequence from infrared absorption spectra[J]. J Am Ceram Soc, 1974, 57(2): 57-61.
[11]Djemai A, Balan E, Morin G, et al. Behavior of paramagnetic iron during the thermal transformations of kaolinite[J]. J Am Ceram Soc, 2001, 84(5): 1017-1024.
[12]Massiot D, Dion P, Alcover J F, et al. 27Al and 29Si NMR study of kaolinite thermal decomposition by controlled rate thermal analysis[J]. J Am Ceram Soc, 1995, 11(78): 2940-2944.
[13]Mackenzie K J D, Hartman J S. MAS NMR evidence for the presence of silicon in the alumina spinel from thermally transformation kaolinite[J]. J Am Ceram Soc, 1996, 79(11): 2980-2982.
[14]Mackenzie K J D, Brown I W M, Meinhold R H, et al. Outstanding problems in the kaolinite-mullite reaction sequence investigated by 29Si and 27Al solid-state nuclear magnetic resonance(Ⅰ)—metakaolinite[J]. J Am Ceram Soc, 1985, 68(6): 293-297.
[15]Watanabe T, Shimizu H, Nagasawa K, et al. 29Si-and-27Al-MAS/NMR study of the thermal transformations of kaolinite[J]. Clay Minerals, 1987(22): 37-48.
[16]郭九皋, 何宏平, 王辅亚, 等. 高岭石-莫来石反应系列29Si和27Al MAS NMR 研究[J]. 矿物学报, 1997, 17(3): 250-259.
GUO Jiu-gao, HE Hong-ping, WANG Fu-ya, et al. Kaolinite-mullite reaction series: A 27Al and 29Si MAS NMR study[J]. ACTA Mineralogical Sinica, 1997, 17(3): 250-259.
[17]张实, 张惠芬. 高岭石的热稳定性和热处理产物的DTA, IR和EPR研究[J]. 矿物岩石, 1992, 12(2): 28-33.
ZHANG Shi, ZHANG Hui-feng. Investigetion of heat-stability and heat-treated products of kaolinite with DTA, IR and EPR[J]. Mineralogy and Petrology, 1992, 12(2): 28-33.
[18]Suitch P R. Mechanism for dehydroxylation of kaolinite, dickite, and nacrite from room temperature to 455℃[J]. J Am Ceram Soc, 1986, 69(1): 61-65.
[19]Anthony G D, Gran P D. Kinetics of kaolinite dehydroxylation[J]. J Am Ceram Soc, 1974, 57(3): 132-135.
[20]Johnson H B, Kessler F. Kaolinite dehydroxylation kinetics[J]. J Am Ceram Soc, 1969, 52(4): 199-204.
[21]Brindley G W, Sharp J H, Patterson J H, et al. Kinetics and mechanism of dehydration process(Ⅰ): temperature and vapor pressure dependence of dehydroxylation of kaolinite[J]. Am Mineral, 1967, 52(1-2): 201-211.
[22]Brindley G W, Nakahira M. Kinetics of dehydroxylation of kaolinite and halloysite[J]. J Am Ceram Soc, 1957, 40(10): 346-350.
[23]Redfern S A T. The kinetics of dehydroxylation of kaolinite[J]. Clay minerals, 1987, 22: 447-456.
[24]Holt J B, Cutler I B, Wadsworth M E. Rate of dehydroxylation of kaolinite in vacuum[J]. J Am Ceram Soc, 1962, 45: 133-136.
[25]Criado J M, Ortega A, Real C, et al. Re-examination of kinetics of dehydro-xylation of kaolinite[J]. Clay Minerals, 1984(19): 653-661.
[26]沈兴. 差热、 热重分析与非等温固相反应动力学[M]. 北京: 冶金工业出版社, 1995. 8.
SHENG Xin. DTA, TGA and Non-isothermal Kinetics of Solid-reactions[M]. Beijing: Metallurgical industry Press, 1995. 8.
(编辑龙怀中)
基金项目: 国家重点基础研究发展规划资助项目(G1999064901)
收稿日期: 2004-11-26; 修订日期: 2005-03-08
作者简介: 姜 涛(1963-), 男, 博士, 教授.
通讯作者: 李光辉, 博士, 副教授; 电话: 0731-8710225; 传真: 0731-8710225; E-mail: liguangh@mail.csu.edu.cn